千米深井提升機主軸多失效模式可靠性評估方法與流程
2023-06-30 01:19:11
本發明是一種針對千米深井提升機主軸並考慮失效模式概率相關時的機械產品的系統可靠性評估方法,屬於機械結構可靠性技術研究領域。
背景技術:
我國目前大多數煤井都是淺井,深至地面500~800m,而煤炭資源埋藏深度在1000~2000m的約佔總儲量的53%,必須採用千米深井提升系統(包括提升機、提升容器、提升鋼絲繩等)。作為提升機的主要承載部件,主軸承擔了提升、下放載荷的全部扭矩,同時也承受著兩側鋼絲繩的拉力。隨著井深達到千米以上,提升機最大靜張力以及主軸捲筒的纏繞層數大大增加,導致鋼絲繩在捲筒上產生遠大於現有結構的纏繞壓力,鋼絲繩作用在主軸上的拉力以及扭矩也顯著增加。當井深達到2000m時,提升機終端靜載荷將達到240t以上,經濟提升速度將達到20m/s以上,由此產生的巨大動載荷將嚴重危及主軸的使用壽命。因此,千米深井提升機對主軸的可靠性提出了更高的要求。
千米深井提升機主軸的故障種類較多,且形式各異,而強度失效和剛度失效是影響提升機安全、穩定工作的最主要的失效模式。由於激勵作用的同源性和表徵系統特徵參數的同一性,使得提升機主軸的故障間普遍存在相關性,忽略這一特徵將難以獲得準確的失效數據和可靠性信息。
技術實現要素:
發明目的:本發明的目的是為解決千米深井提升機主軸多失效模式聯合失效狀態下的系統可靠性評估提供一種可行的概率建模與分析方法。
為了實現上述目的,本發明採用了如下的技術方案:
一種千米深井提升機主軸多失效模式可靠性評估方法,首先,根據主軸的結構尺寸建立主軸的參數化三維模型,其次,根據主軸隨機變量的概率屬性,建立隨機變量的抽樣矩陣,並使用有限元方法求解抽樣矩陣下主軸的強度和剛度響應,再次,使用神經網絡方法建立響應與隨機變量矩陣之間的顯式函數,根據強度和剛度設計準則,分別建立強度和剛度失效模式下的顯式功能函數,然後,使用鞍點逼近方法計算兩種失效概率,最後,通過claytoncopula函數構建兩種失效模式間的聯合失效概率模型,使用區間可靠性方法求解聯合失效下的系統可靠性。
其實現步驟具體如下:
步驟1、確定千米深井提升機主軸中尺寸參數、材料屬性參數及工況載荷的均值和方差,確定各參數的分布類型;
步驟2、根據提升機主軸的結構參數,建立主軸的三維參數化模型,將主軸的三維參數化模型導入有限元軟體,進行靜力學分析;
步驟3、根據步驟1所確定的主軸各個基本參數的均值和方差,結合抽樣方法,建立各基本參數的隨機抽樣矩陣;
步驟4、根據隨機抽樣矩陣每一行的參數值,重複生成新的主軸的三維模型,並重新進行有限元分析,獲得新的應力與應變的響應樣本;
步驟5、使用神經網絡方法將隨機抽樣矩陣和應力應變值進行擬合,得到主軸應力應變響應與結構性能參數變化的函數關係;
步驟6、根據提升機主軸強度和剛度的要求,分別建立強度和剛度失效狀態下的可靠性功能函數;根據基本參數的均值和方差,計算其三階矩和四階矩,進而根據已建立的功能函數,求得功能函數的均值、方差、三階矩和四階矩,使用鞍點逼近方法分別計算強度和剛度失效的失效概率;
步驟7、通過統計方法獲得強度失效與剛度失效間的關聯繫數,通過claytoncopula函數建立強度與剛度失效的聯合失效分布,進而結合區間可靠性方法求解失效相關時的系統失效概率。
步驟1具體為:
確定提升機主軸的結構尺寸和材料屬性的均值和方差;
確定提升機主軸的工況,由此確定各工況下主軸所承擔的靜載荷、動載荷、彎矩和扭矩等載荷的均值和方差;
確定上述各參數的分布類型。
步驟2具體為:
通過提升機主軸的參數化建模,生成建模的命令流文件,導出建立的主軸模型,保存在工作目錄中,
通過提升機主軸的有限元分析,生成分析過程的命令流文件,並導出包含分析結果的文本文件,保存在同一工作目錄下;
根據主軸的材料性能參數,建立主軸的有限元模型,並施加彎矩、扭矩及最大靜載荷等外載荷,
其中,主軸的結構參數包括主軸各軸段的直徑、長度,各捲筒的直徑和長度等;材料性能參數包括彈性模量、泊松比和密度。
步驟4具體為:
在設定的工作目錄下,根據所生成的隨機抽樣矩陣,在建模過程的命令流文件中進行變量值的修改,生成新的主軸模型;
使用有限元分析的命令流分析新生成的主軸模型,獲得新的應力應變響應值;
重複上述步驟,直到隨機變量矩陣中的每組隨機變量值都獲得了對應的應力應變響應值。
步驟7具體為:
根據主軸隨機變量的分布類型進行隨機抽樣,並通過步驟6所建立的可靠性功能函數獲得強度與剛度失效之間的計算值;
使用統計方法求得兩失效模式間的秩相關係數,並計算claytoncopula的待定參數;
使用claytoncopula計算強度與剛度的聯合失效概率;
使用二階窄界限理論,代入步驟6所得到的強度失效概率和剛度失效概率以及聯合失效概率,計算提升機主軸的系統失效概率。
本發明方法的優點和積極效果在於:
1)採用wsp(wootton,sergent,phan-tan-luu)抽樣方法能夠建立提升機主軸中多維隨機變量的抽樣矩陣,在保證非線性函數擬合精度的基礎上,降低基於有限元分析的試驗設計次數;
2)考慮了強度與剛度失效間的概率相關性,相對於失效獨立假設,能夠更加準確和合理地評估提升機主軸的系統可靠性;
3)提升機主軸強度與剛度失效表現為較強的正相關性,採用claytoncopula能夠準確地建立這種正相關的概率模型,避免了gaussiancopula只能描述對稱相關的缺點,從而提高提升機主軸系統可靠性評估的精度。
附圖說明
圖1為本發明的千米深井提升機主軸多失效模式可靠性評估方法的實現流程圖。
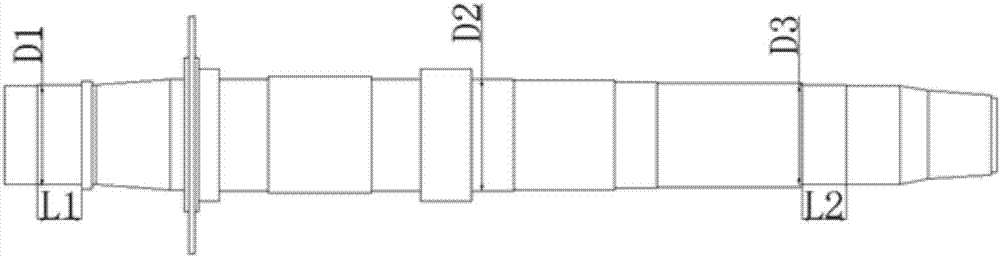
圖2為提升機主軸的二維結構圖。
圖3為claytoncopula函數的概率密度圖。
圖4為claytoncopula函數的散點圖。
其中,d1為主軸與左側軸承配合處的直徑,l1為主軸與左側軸承配合處的長度,d2為主軸安裝套筒處的直徑,d3為主軸與右側軸承配合處的直徑,l2為主軸與右側軸承配合處的長度。
具體實施方式:
下面結合附圖和實施例對本發明做進一步的說明。
如圖1所示,本發明所提出的考慮多失效模式的系統可靠性評估方法,包含如下步驟:
步驟1、通過現場測繪和提升機主軸的設計圖紙,獲取尺寸參數、材料屬性及工況載荷的均值和方差,確定各參數的分布類型;
步驟2、根據提升機主軸的結構參數,建立主軸的三維參數化模型,將主軸的三維參數化模型導入有限元軟體,進行靜力學分析。
步驟3、根據步驟1所確定的主軸各個基本參數的均值和方差,結合wsp(wootton,sergent,phan-tan-luu)抽樣方法,建立各基本參數的隨機抽樣矩陣;
步驟4、根據隨機抽樣矩陣每一行的參數值,重複生成新的主軸的三維模型,並重新進行有限元分析,獲得新的應力與應變的響應樣本;
步驟5、使用神經網絡方法將隨機抽樣矩陣(輸入樣本)和應力應變值(響應樣本)進行擬合,得到主軸應力應變響應與結構性能參數變化的函數關係;
步驟6、根據提升機主軸強度和剛度的要求,分別建立強度和剛度失效狀態下的可靠性功能函數;根據基本參數的均值和方差,計算其三階矩和四階矩,進而根據已建立的功能函數,求得功能函數的均值、方差、三階矩和四階矩,使用鞍點逼近方法分別計算強度和剛度失效的失效概率;
步驟7、通過統計方法獲得強度失效與剛度失效間的關聯繫數,通過claytoncopula函數建立強度與剛度失效的聯合失效分布,進而結合區間可靠性方法求解失效相關時的系統失效概率。
實施例:
為了更充分地了解該發明的特點及工程適用性,本發明針對如圖2所示擬建的千米深井提升機主軸結構,進行強度和剛度相關的系統可靠性求解。
該主軸結構承受彎矩和扭矩作用。綜合主軸的結構尺寸和載荷條件,可以建立主軸隨機抽樣矩陣,並通過有限元方法獲得主軸應力應變的響應樣本矩陣。通過神經網絡方法建立響應與輸入矩陣的顯式函數關係,進而根據提升機主軸的強度準則和剛度準則建立兩種失效模式的顯式極限狀態方程,即強度失效的極限狀態方程以及剛度失效的極限狀態方程。表1給出了本實施例中主軸隨機變量的概率信息。其中,d1為主軸與左側軸承配合處的直徑,l1為主軸與左側軸承配合處的長度,d2為主軸安裝套筒處的直徑,d3為主軸與右側軸承配合處的直徑,l2為主軸與右側軸承配合處的長度。
表1主軸中隨機變量的概率統計特性
該實施例中利用本發明中所提出的失效概率的求解方法得到強度失效模式下的失效概率為pf1=0.003241,剛度失效概率為pf2=0.005173。通過隨機抽樣方法生成隨機主軸結構隨機變量的n個樣本值,並代入兩種失效模式的顯式極限狀態方程,分別計算得到n個響應值,並利用matlab中的命令計算得到強度響應向量和剛度響應向量之間的相關係數,並估計claytoncopula函數的待定參數。將失效概率pf1和pf2代入公式
式中,m表示提升機主軸失效模式的個數,pf1表示提升機主軸失效模式中的最大失效概率,pfi表示第i個失效模式的失效概率,pfij表示第i個和第j個失效模式間的聯合失效概率,pfs表示提升機主軸失效相關的系統失效概率。
得到考慮主軸結構強度和剛度相關性的失效概率為pfs=0.008536。通過仿真方法計算得到的系統失效概率為pfsm=0.008746。
綜上所述,本方法提出了一種針對千米深井提升機主軸,考慮強度和剛度失效相關性的系統可靠性求解方法。首先,根據主軸的結構尺寸建立主軸的參數化三維模型,其次,根據主軸隨機變量的概率屬性,建立隨機變量的抽樣矩陣,並使用有限元方法求解抽樣矩陣下主軸的強度和剛度響應,再次,使用神經網絡方法建立響應與隨機變量矩陣之間的顯式函數,根據強度和剛度設計準則,分別建立強度和剛度失效模式下的顯式功能函數,然後,使用鞍點逼近方法計算兩種失效概率,最後,通過claytoncopula函數構建兩種失效模式間的聯合失效概率模型,使用區間可靠性方法求解聯合失效下的系統可靠性。
本發明未詳細闡述的部分屬於本領域研究人員的公知技術。
