基於傳輸線迭代的2D軸對稱非線性靜磁場模型的求解方法與流程
2023-06-09 08:46:52
本發明涉及數值計算領域,具體而言,涉及一種基於傳輸線迭代法的非線性靜磁場模型的有限元求解方法,該方法主要針對2D軸對稱非線性靜態電磁場進行求解。
背景技術:
有限元法是工業設計中最常用的數值計算方法,被諸多商用仿真軟體採用,應用廣泛。然而,隨著求解模型的日益複雜化以及分網單元數目的不斷增多,以傳統的牛頓迭代法為核心的非線性有限元求解方法面臨著求解耗時嚴重的問題,這直接關係到產品研發的速度和效率。
有限元問題的求解的核心在於求解線性方程組,而對於非線性問題來說,傳統的牛頓迭代法每一步都要利用新的迭代結果重新生成有限元模型的全局矩陣,隨著模型分網的不斷增大,全局矩陣的維度不斷變大,每一步矩陣的LU分解等消耗的時間會相應的增大,總體的求解時間可能隨著分網的變密而成幾何式增大。
因此,需要研究一種新的迭代方法,以解決牛頓迭代法求解有限元非線性問題時帶來的求解時間長,效率低的問題。
技術實現要素:
本發明提供了一種基於傳輸線迭代法的2D軸對稱非線性靜磁場模型的有限元求解方法,用以解決牛頓迭代法求解有限元非線性問題時帶來求解時間長,效率低的問題。
為了達到上述目的,本發明提供了一種基於傳輸線迭代法的2D軸對稱非線性靜磁場模型的有限元求解方法,其包括以下步驟:
S1:確定待求解的變量以及求解域,待求解的變量為一2D軸對稱非線性靜磁場的磁勢,2D軸對稱非線性靜磁場由通電線圈中的電流產生,通電線圈周圍的各元件均為鐵磁材料,求解域為2D軸對稱非線性靜磁場所在的區域;
S2:建立一平面x-y坐標系,以2D軸對稱非線性靜磁場的對稱軸為y軸,在y軸上選定其中一點為原點,並設定經過原點並與y軸垂直的直線為x軸,即x-y平面為2D軸對稱非線性靜磁場所在區域一過對稱軸的截面所在的平面;
S3:列出2D軸對稱非線性靜磁場中的控制方程和邊界條件式並組成一微分方程組,其控制方程為:
其中,J為電流密度變量,μ為三角單元的磁導率,A為磁勢,
邊界條件式為:
Γ1:A=0,
Γ1表示磁勢A在邊界Γ1上的分布,Γ2表示磁勢A沿邊界的外法線方向的變化率,
S4:使用三角單元對求解域進行分網,得到包含多個三角單元的有限元網絡,該有限元網絡中的三角單元總個數為N,節點總個數為M,並分別對三角單元和節點進行1~N和1~M的編號,其中1000≤N≤3000;
S5:根據微分方程組的泛函形式,推導出每一個三角單元的單元矩陣[Ye]和激勵源單元矩陣[Je],其中,每一[Ye]均為3×3的矩陣,每一[Je]均為1×3的矩陣:
[Je]=[Jl Jm Jn],
l、m、n分別為推導每一三角單元的[Ye]和[Je]時,三角單元的三個頂點的編號,
r和s分別為三角單元的三個頂點編號1、m和n中的其中兩個頂點編號,
x1、xm和xn分別為節點l、節點m和節點n在平面坐標系中的橫坐標,y1、ym和yn分別為節點l、節點m和節點n在平面坐標系中的縱坐標,Δ為節點l、節點m和節點n組成的三角單元的面積;
S6:根據得到的每一個三角單元的單元矩陣[Ye]和激勵源單元矩陣[Je],對N個三角單元進行有限元裝配,得到全局矩陣Y和J,其中Y為M×M矩陣,J為M×1矩陣;
S7:求解非線性方程組YA=J,得到2D軸對稱非線性靜磁場中每個節點的磁勢A,其中A為M×1的節點磁勢矩陣,A=[A1 A2 … AM]T;
S8:根據步驟S8中計算得到的節點磁勢矩陣A,按照以下各式計算每一個三角單元的磁感應強度B,其中,
S9:根據鐵磁材料的B-H曲線以及步驟S8中計算得到的每一個三角單元的磁感應強度B,並計算出每一個三角單元的磁導率μ;
S10:以步驟S4中的分網結果為基礎,對求解域進行精細的三角分網,得到三角單元總個數為N'、節點總個數為M'的有限元網絡,並分別對三角單元和節點進行1~N'和1~M'的編號;
S11:按照步驟S5中的方法,對步驟S10中得到的有限元網絡再次計算每個三角單元的單元矩陣[Ye]和激勵源單元矩陣[Je];
S12:有限元網絡轉化為電路模型,將步驟S11中得到的單元矩陣[Ye]視為電路的導納矩陣,激勵源單元矩陣[Je]視為每個節點與地之間的電流源矩陣,對有限元網絡中的每一個三角單元均建立一個等效電路網絡,建立等效電路網絡的方法如下:
將單元矩陣[Ye]對角線上的元素視為自導,非對角線上的元素視為互導,
對於非對角線上的元素,若Yrs>0,則在三角單元對應的等效電路網絡中的節點r和節點s之間設置一受控電流源,該受控電流源中的電流大小為UrsYrs,方向為從節點r流向節點s,其中Urs為節點r與節點s之間的磁勢差,
對於非對角線上的元素,若Yrs<0,則在三角單元對應的等效電路網絡中的節點r和節點s之間設置一純電阻,該純電阻的導納為|Yrs|,
若有限元單元矩陣[Ye]的第r行的所有元素之和不等於0,當第r行所有元素之和大於零時,在節點r與地之間設置一純電阻,該純電阻的導納為Yrl+Yrm+Yrn,當第r行所有元素之和小於零時,則在節點r與地之間設置一受控電流源,該受控電流源中的電流大小為Ur0·|Yrl+Yrm+Yrn|,方向為從節點r流向地,其中Ur0為節點r與地之間的磁勢差,
在每一節點與地之間均設置一電流源,節點l、節點m、節點n與地之間的電流源中的電流大小分別為Jl、Jm、Jn,電流方向為由地流向節點;
S13:組裝電路,將步驟S12中建立的每一個三角單元對應的等效電路網絡通過節點進行連接,組裝成一個完整的非線性電路網絡,該非線性電路網絡等效為包含一線性網絡與多個非線性待求元件的電路;
S14:對於步驟S13中得到的非線性電路網絡,為了使用傳輸線迭代方法進行求解,需要在非線性元件與線性網絡之間添加一段傳輸線,由於傳輸線對信號傳輸的延時作用,電路的非線性求解過程包括入射階段和反射階段,
入射階段,非線性電路元件的電壓信號向線性網絡進行入射,等效為傳輸線導納與虛擬電流源的並聯,
反射階段,電壓信號由線性網絡傳向非線性元件,對非線性元件進行求解,如此不斷迭代入射階段和反射階段,直到電路達到穩態,
(一)在線性部分與非線性元件之間添加一段傳輸線,傳輸線的導納的計算方法如下:
(1)確定每一個三角單元的磁導率μ的估計值,檢查經過步驟S10分網後得到的三角單元的重心對應的第一次分網的三角單元,並將對應的第一次分網的三角單元的磁導率設為三角單元的磁導率,
(2)非線性元件的導納是一個關於磁導率μ的變量,將上一步得到的μ值代入到非線性元件表達式,得到的結果作為對應的傳輸線的導納值,
(二)設迭代開始時每一節點的電壓均為0,當第n個節點電壓信號以Vin反射到線性網絡時,每一非線性待求元件等效為一導納和一電流源的並聯電路,其中,導納為對應的傳輸線導納Yn,電流源中的電流值為2VinYn,對該等效電路進行求解,得到每一節點的電壓值Vin,
(三)根據各個節點的電壓值,利用非線性元件與電壓之間的關係式,計算並更新非線性元件的導納值,
(四)計算各個節點向非線性元件入射的電壓值Vrn,節點n處的Vrn=Vn-Vin,
(五)入射過程,每一非線性待求元件等效為一導納與一電流源的並聯電路,其中,導納為對應的傳輸線導納Yn,電流源中的電流值為2VrnYn,得到每一非線性元件兩端的電壓
(六)計算各個節點向線性網絡入射的電壓值Vin,節點n處的
(七)重複步驟(二)~(六),直至相鄰兩次迭代中,步驟(二)所求的電壓值Vn達到預設的收斂誤差,此時計算得到的各節點的電壓值Vn即為所求電壓值,
S15:根據每一節點的電壓值繪製2D軸對稱非線性靜磁場中的磁勢雲圖。
在本發明的一實施例中,步驟S14中(二)對等效電路的求解為使用節點電壓法進行求解,其步驟為:
(一)計算得到矩陣YV=I,其中Y為電路導納矩陣,由於迭代過程中,導納矩陣Y保持不變,僅需計算一次,V為待求節點電壓,I為節點電流;
(二)迭代第一步對矩陣Y進行LU分解,即Y=LU,其中L為單位下三角矩陣,U為上三角矩陣,之後的每一次迭代,無需計算此步,直接計算步驟(三);
(三)使用公式V=U-1(L-1I)求解節點電壓V。
在本發明的一實施例中,步驟S14中(五),入射過程中,每一非線性元件兩端電壓的求解是獨立的,在此使用多核並行技術同時對多個非線性元件兩端電壓進行求解。
本發明提供的基於傳輸線迭代法的2D軸對稱非線性靜磁場模型的有限元求解方法解決了牛頓迭代法求解有限元非線性問題時帶來求解時間長,效率低的問題。本發明中的每一步驟均無需再次計算全局矩陣,只需要進行一次全局矩陣的LU分解,然後即可重複使用,從而節省計算時間;同時,該方法非常適合使用並行算法進行加速,能夠進一步的加快有限元問題的求解。相對於傳統的牛頓迭代法,本發明在求解時間上有著很大的優勢,有著廣闊的應用前景。
附圖說明
為了更清楚地說明本發明實施例或現有技術中的技術方案,下面將對實施例或現有技術描述中所需要使用的附圖作簡單地介紹,顯而易見地,下面描述中的附圖僅僅是本發明的一些實施例,對於本領域普通技術人員來講,在不付出創造性勞動的前提下,還可以根據這些附圖獲得其他的附圖。
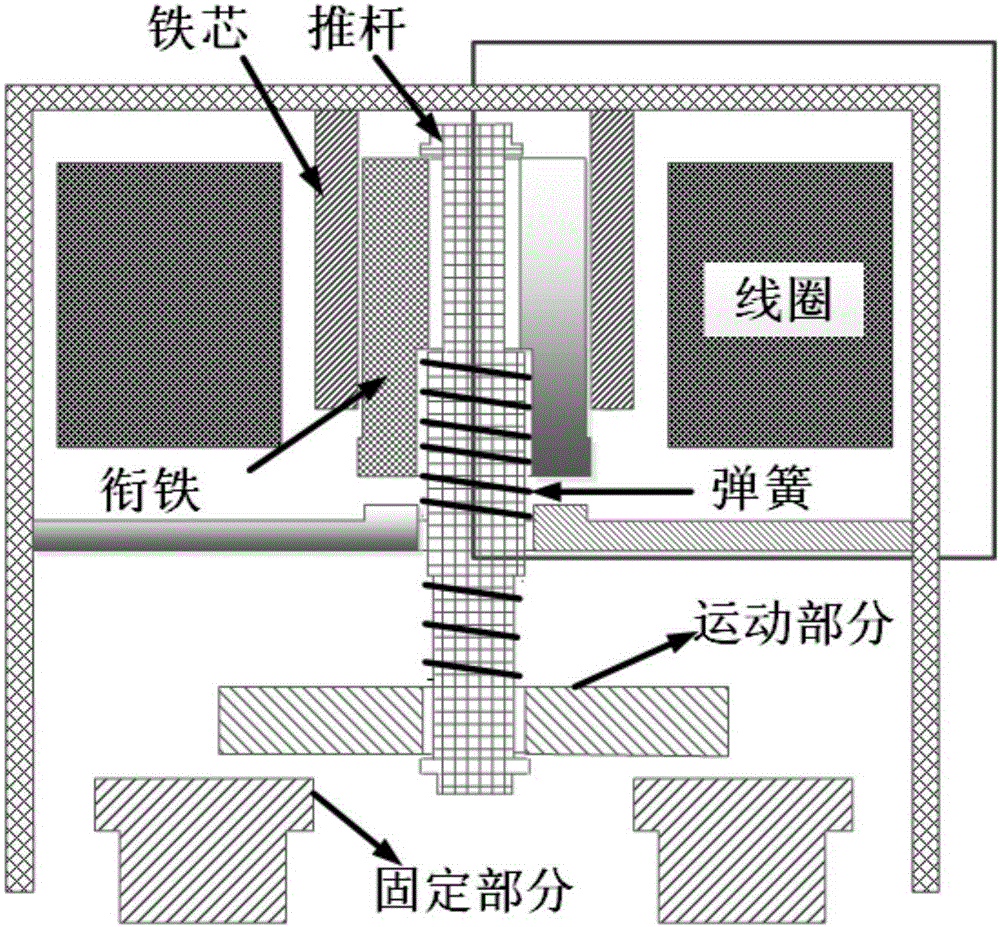
圖1為產生一2D軸對稱非線性靜磁場的接觸器機械結構示意圖;
圖2為與圖1對應的靜磁場的有限元模型區域示意圖;
圖3a為對求解域進行首次分網(粗糙分網)的示意圖;
圖3b為對求解域進行再次分網(精細分網)的示意圖;
圖4為求解域中的三角單元的示意圖;
圖5為等效電路網絡的示意圖;
圖6為對三角單元進行組裝的示意圖;
圖7為傳輸線迭代等效示意圖;
圖8為反射過程的等效示意圖;
圖9為入射過程的等效示意圖;
圖10為靜磁場中的磁勢雲圖;
圖11為傳統牛頓迭代法與傳輸線迭代法求解時間對比;
圖12為牛頓迭代法與傳輸線迭代法不同分網大小計算時間對比;
圖13為牛頓迭代法與傳輸線迭代法單步計算時間對比。
具體實施方式
下面將結合本發明實施例中的附圖,對本發明實施例中的技術方案進行清楚、完整地描述,顯然,所描述的實施例僅僅是本發明一部分實施例,而不是全部的實施例。基於本發明中的實施例,本領域普通技術人員在沒有付出創造性勞動前提下所獲得的所有其他實施例,都屬於本發明保護的範圍。
本發明提供的基於傳輸線迭代法的2D軸對稱非線性靜磁場模型的有限元求解方法包括以下步驟:
S1:確定待求解的變量以及求解域,待求解的變量為一2D軸對稱非線性靜磁場的磁勢,2D軸對稱非線性靜磁場由通電線圈中的電流產生,通電線圈周圍的各元件均為鐵磁材料,求解域為2D軸對稱非線性靜磁場所在的區域;
圖1為產生一2D軸對稱非線性靜磁場的接觸器機械結構示意圖,如圖所示,圖1中為一接觸器,其中的線圈中通有電流,線圈周圍的鐵芯、推桿、銜鐵等的材質均為鐵磁材料,該接觸器周圍的靜磁場以推桿為中心而軸對稱,因此,可以先以靜磁場的其中任意一個截面(如圖中的方框部分)為研究對象。
圖2為與圖1對應的靜磁場的有限元模型區域示意圖,該有限元模型區域為圖1中的俯視區域的右側部分,該區域也就是本發明針對的求解域。
S2:建立一平面x-y坐標系,以2D軸對稱非線性靜磁場的對稱軸為y軸,在y軸上選定其中一點為原點,並設定經過原點並與y軸垂直的直線為x軸,即x-y平面為2D軸對稱非線性靜磁場所在區域一過對稱軸的截面所在的平面;
S3:列出2D軸對稱非線性靜磁場中的控制方程和邊界條件式並組成一微分方程組,其控制方程為:
其中,J為電流密度變量,μ為三角單元的磁導率,A為磁勢,
邊界條件式為:
Γ1:A=0,
Γ1表示磁勢A在邊界Γ1上的分布,Γ2表示磁勢A沿邊界的外法線方向的變化率,
S4:使用三角單元對求解域進行分網,得到包含多個三角單元的有限元網絡,該有限元網絡中的三角單元總個數為N,節點總個數為M,並分別對三角單元和節點進行1~N和1~M的編號,其中1000≤N≤3000;
圖3為對求解域進行首次分網(粗糙分網)的示意圖。
S5:根據微分方程組的泛函形式,推導出每一個三角單元的單元矩陣[Ye]和激勵源單元矩陣[Je],其中,每一[Ye]均為3×3的矩陣,每一[Je]均為1×3的矩陣:
[Je]=[Jl Jm Jn],
圖4為求解域中的三角單元的示意圖,l、m、n分別為推導每一三角單元的[Ye]和[Je]時,三角單元的三個頂點的編號,
r和s分別為三角單元的三個頂點編號1、m和n中的其中兩個頂點編號,
x1、xm和xn分別為節點l、節點m和節點n在平面坐標系中的橫坐標,y1、ym和yn分別為節點l、節點m和節點n在平面坐標系中的縱坐標,Δ為節點l、節點m和節點n組成的三角單元的面積;
S6:根據得到的每一個三角單元的單元矩陣[Ye]和激勵源單元矩陣[Je],對N個三角單元進行有限元裝配,得到全局矩陣Y和J,其中Y為M×M矩陣,J為M×1矩陣;
S7:求解非線性方程組YA=J,得到2D軸對稱非線性靜磁場中每個節點的磁勢A,其中A為M×1的節點磁勢矩陣,A=[A1 A2…AM]T;
S8:根據步驟S8中計算得到的節點磁勢矩陣A,按照以下各式計算每一個三角單元的磁感應強度B,其中,
S9:根據鐵磁材料的B-H曲線以及步驟S8中計算得到的每一個三角單元的磁感應強度B,並計算出每一個三角單元的磁導率μ;
S10:以步驟S4中的分網結果為基礎,對求解域進行精細的三角分網,圖3b為對求解域進行再次分網(精細分網)的示意圖,得到三角單元總個數為N'、節點總個數為M'的有限元網絡,並分別對三角單元和節點進行1~N'和1~M'的編號;
S11:按照步驟S5中的方法,對步驟S10中得到的有限元網絡再次計算每個三角單元的單元矩陣[Ye]和激勵源單元矩陣[Je];
S12:有限元網絡轉化為電路模型,將步驟S11中得到的單元矩陣[Ye]視為電路的導納矩陣,激勵源單元矩陣[Je]視為每個節點與地之間的電流源矩陣,對有限元網絡中的每一個三角單元均建立一個等效電路網絡,圖5為等效電路網絡的示意圖,如圖所示,建立等效電路網絡的方法如下:
將單元矩陣[Ye]對角線上的元素視為自導,非對角線上的元素視為互導,
對於非對角線上的元素,若Yrs>0,則在三角單元對應的等效電路網絡中的節點r和節點s之間設置一受控電流源,該受控電流源中的電流大小為UrsYrs,方向為從節點r流向節點s,其中Urs為節點r與節點s之間的磁勢差,
對於非對角線上的元素,若Yrs<0,則在三角單元對應的等效電路網絡中的節點r和節點s之間設置一純電阻,該純電阻的導納為|Yrs|,
若有限元單元矩陣[Ye]的第r行的所有元素之和不等於0,當第r行所有元素之和大於零時,在節點r與地之間設置一純電阻,該純電阻的導納為Yrl+Yrm+Yrn,當第r行所有元素之和小於零時,則在節點r與地之間設置一受控電流源,該受控電流源中的電流大小為Ur0·|Yrl+Yrm+Yrn|,方向為從節點r流向地,其中Ur0為節點r與地之間的磁勢差,
在每一節點與地之間均設置一電流源,節點l、節點m、節點n與地之間的電流源中的電流大小分別為Jl、Jm、Jn,電流方向為由地流向節點;
S13:組裝電路,圖6為對三角單元進行組裝的示意圖,如圖所示,將步驟S12中建立的每一個三角單元對應的等效電路網絡通過節點進行連接,組裝成一個完整的非線性電路網絡,該非線性電路網絡等效為包含一線性網絡與多個非線性待求元件的電路;
S14:對於步驟S13中得到的非線性電路網絡,為了使用傳輸線迭代方法進行求解,需要在非線性元件與線性網絡之間添加一段傳輸線,由於傳輸線對信號傳輸的延時作用,電路的非線性求解過程包括入射階段和反射階段,圖7為傳輸線迭代等效示意圖,
入射階段,非線性電路元件的電壓信號向線性網絡進行入射,等效為傳輸線導納與虛擬電流源的並聯,
反射階段,電壓信號由線性網絡傳向非線性元件,對非線性元件進行求解,如此不斷迭代入射階段和反射階段,直到電路達到穩態,
(一)在線性部分與非線性元件之間添加一段傳輸線,傳輸線的導納的計算方法如下:
(1)確定每一個三角單元的磁導率μ的估計值,檢查經過步驟S10分網後得到的三角單元的重心對應的第一次分網的三角單元,並將對應的第一次分網的三角單元的磁導率設為三角單元的磁導率,
(2)非線性元件的導納是一個關於磁導率μ的變量,將上一步得到的μ值代入到非線性元件表達式,得到的結果作為對應的傳輸線的導納值,
(二)設迭代開始時每一節點的電壓均為0,當第n個節點電壓信號以Vin反射到線性網絡時,每一非線性待求元件等效為一導納和一電流源的並聯電路,其中,導納為對應的傳輸線導納Yn,電流源中的電流值為2VinYn,對該等效電路進行求解,得到每一節點的電壓值Vin,圖8為反射過程的等效示意圖,
(三)根據各個節點的電壓值,利用非線性元件與電壓之間的關係式,計算並更新非線性元件的導納值,
(四)計算各個節點向非線性元件入射的電壓值Vrn,節點n處的Vrn=Vn-Vin,
(五)入射過程,每一非線性待求元件等效為一導納與一電流源的並聯電路,其中,導納為對應的傳輸線導納Yn,電流源中的電流值為2VrnYn,得到每一非線性元件兩端的電壓圖9為入射過程的等效示意圖,
(六)計算各個節點向線性網絡入射的電壓值Vin,節點n處的
(七)重複步驟(二)~(六),直至相鄰兩次迭代中,步驟(二)所求的電壓值Vn達到預設的收斂誤差,此時計算得到的各節點的電壓值Vn即為所求電壓值,
S15:根據每一節點的電壓值繪製2D軸對稱非線性靜磁場中的磁勢雲圖,如圖10所示為靜磁場中的磁勢雲圖。
在本發明中,步驟S14中(二)對等效電路的求解可以使用節點電壓法進行求解,其步驟為:
(一)計算得到矩陣YV=I,其中Y為電路導納矩陣,由於迭代過程中,導納矩陣Y保持不變,僅需計算一次,V為待求節點電壓,I為節點電流;
(二)迭代第一步對矩陣Y進行LU分解,即Y=LU,其中L為單位下三角矩陣,U為上三角矩陣,之後的每一次迭代,無需計算此步,直接計算步驟(三);
(三)使用公式V=U-1(L-1I)求解節點電壓V。
在本發明中,步驟S14中(五),入射過程中,每一非線性元件兩端電壓的求解是獨立的,在此使用多核並行技術同時對多個非線性元件兩端電壓進行求解。
下面闡述本發明的有益技術效果:
相比傳統牛頓迭代法求解非線性有限元問題,使用本發明提供的傳輸線迭代法,能夠非常顯著的減少計算所用的時間。圖11~圖13對比了傳統牛頓迭代法與傳輸線迭代法的計算效率。圖11中,在單核計算下,傳統的牛頓迭代法計算時間幾乎是傳輸線迭代法的6倍,使用本發明提供的方法,求解速度得到了很大的提升;圖12中,隨著求解模型的分網單元增加,牛頓迭代法與傳輸線迭代法的求解時間比值不斷增大,說明出本發明能夠有效的處理有限元模型變複雜的情況;圖13顯示的是這兩種方法的單步求解時間對比,可見,本發明具有非常顯著的時間優勢,能大幅度提高計算效率。
本發明提供的基於傳輸線迭代法的2D軸對稱非線性靜磁場模型的有限元求解方法解決了牛頓迭代法求解有限元非線性問題時帶來求解時間長,效率低的問題。本發明中的每一步驟均無需再次計算全局矩陣,只需要進行一次全局矩陣的LU分解,然後即可重複使用,從而節省計算時間;同時,該方法非常適合使用並行算法進行加速,能夠進一步的加快有限元問題的求解。相對於傳統的牛頓迭代法,本發明在求解時間上有著很大的優勢,有著廣闊的應用前景。
本領域普通技術人員可以理解:附圖只是一個實施例的示意圖,附圖中的模塊或流程並不一定是實施本發明所必須的。
本領域普通技術人員可以理解:實施例中的裝置中的模塊可以按照實施例描述分布於實施例的裝置中,也可以進行相應變化位於不同於本實施例的一個或多個裝置中。上述實施例的模塊可以合併為一個模塊,也可以進一步拆分成多個子模塊。
最後應說明的是:以上實施例僅用以說明本發明的技術方案,而非對其限制;儘管參照前述實施例對本發明進行了詳細的說明,本領域的普通技術人員應當理解:其依然可以對前述實施例所記載的技術方案進行修改,或者對其中部分技術特徵進行等同替換;而這些修改或者替換,並不使相應技術方案的本質脫離本發明實施例技術方案的精神和範圍。
