基於Fisher法的光伏併網系統穩態電能質量評估方法與流程
2023-06-08 12:42:06
本發明涉及一種電能質量評估方法。
背景技術:
隨著我國經濟的快速發展,國內對電力的需求逐步增大。為了解決日益嚴重的能源消耗問題,光伏、風電等分布式發電技術得到迅速發展並廣泛接入到電力系統中,目前已經取得了一些成果。但是當這些新型發電系統併網後,會對當地電網造成一定的衝擊和影響,這種影響可能會造成頻率偏差、電壓波動、電壓閃變、諧波畸變等一系列問題,從而引起電網電能質量下降。為保證電網的安全可靠性,在分布式發電入網前需要進行電能質量分析,如不達標則需要配套相應的治理措施。準確而全面的電能質量綜合評估對實現分布式電源併網具有重要的意義。
電能質量綜合評估是一個多指標評估過程,其基本思想是將多個指標轉化為一個能夠反映綜合情況的指標來進行評價。目前關於綜合評估含分布式發電系統電能質量方面,已經提出的方法有突變決策法、概率評估法、數據包絡分析法等。
技術實現要素:
本發明的目的是提供一種新的光伏併網系統穩態電能質量評估方法。本發明的技術方案如下:
一種基於Fisher判別分類法的光伏併網系統穩態電能質量評估方法,步驟如下:
1)針對電能質量評估的頻率偏差、電壓偏差、電壓波動、閃變、諧波、三相不平衡等六個指標,結合我國電能質量國家標準,將六個指標劃分為Q1~Q5五個等級,分別代表電能質量為優質、良好、中等、合格以及不合格。
2)獲取一定數量的訓練樣本;
3)根據電能質量的標準,各類電能質量的指標均有上下限值,當樣本中各項電能指標都落在某類電能質量所規定的範圍內,該樣本則屬於相應級別,對標準類別進行線性插值得到足夠多的判別樣本;
4)對Q1、Q2、Q3、Q4等級內得到的多個判別樣本和待評估電能質量數據進行標準化處理,消除不同指標之間的量綱影響;
5)利用標準化處理後的樣本數據建立Fisher判別模型,並得出典則判別函數,然後利用回代法將樣本數據代入到建立好的模型中,檢驗模型誤判率;至此,基於Fisher判別分類法的光伏併網系統穩態電能質量評估模型建立。
5)將測量數據代入到所建立Fisher模型判別函數中,所得函數值落在哪個區間便可以判定該地區電能質量所屬等級,完成電能質量評估並得出結論。
應用Fisher判別分析法對穩態電能質量進行評估時,不用考慮指標之間的權重問題,從而避免在確定指標權重時由於方法選取不同而造成的評估結果差異。同時,該方法適用於選取任意多的電能質量評估指標模型,提高了應用範圍。
附圖說明
圖1.光伏系統穩態電能質量評估的指標體系
圖2.用Fisher法進行電能質量評估流程圖
具體實施方式
下面對本發明進行詳細說明
(1)Fisher判別分析法原理
Fisher判別分析方法的基本思想是投影,可以將高位數據點投影到低維空間中,從而克服由於維數較高而引起的「維數禍根」。Fisher判別分析法是根據類間距離最大、類內距離最小的原則來得到判別函數,然後利用判別函數判定待判樣品所屬類別。基本思想是從已知樣本中篩選出能代表較多信息的變量,建立判別函數並給出待分類對象的類別特徵。
假設有m個已知類別的總體G1,G2...Gm,從總體Gi中各抽取ni個樣本:
為在軸上的投影。其中,α=1,2,3...ni,i=1,2...m。向量μ=(μ1,μ2...μp)T表示p維空間一個方向。
樣本總數n,滿足
求取組內樣本均值和總樣本均值並表示如下:
於是,可以求得組內差:
組間差為
為了使判別函數很好地區別不同總體的樣本,則需要滿足不同總體的組間離差越大越好,組內離差越小越小。令
利用拉格朗日乘數法,可以轉化為:
(W-1B-λI)μ=0...............................................(9)
可以看出λ是W-1B的特徵值,μ就是所對應的特徵向量,I為組內離差平方和與組間離差平方和的比值。將得到的特徵值λ按大小順序排序為λ1≥λ2≥...λs,s≤p,相應的特徵向量為μ1,μ2...μs這樣就可以得出s個判別函數,yj=μjTx,j=1,2...s,x=(x1,x2...xp)T表示待評估對象。取包含信息較多的前M個函數,即:
yj=μjTx=μ1jx1+μ2jx2+...+μpjxp.....................(10)
其中,μj=(μ1j,μ2j...μpj)T j=1,2...M
根據上述M個判別函數,可對每個待判樣品作出判別。
Fisher判別分析的判別過程如下:
(1)將待判數據Xα=(xα1,xα2...xαp)T帶入每個判別函數,得到M個函數:
j=1,2...M
(2)將每一類的均值樣本帶入判別函數,得:
j=1,2...M,i=1,2...m
(3)計算待判樣本Xα與均值樣本的判別函數值之間的歐式距離:
從這m個值中選出最小值,則待判數據就被劃分為屬於該等級。
為了考察上述判別準則是否實用,可以採用將訓練樣本回代的方法來計算誤判率。將G1,G2...Gm的n個樣本帶入建立的判別函數,利用判別準則進行判別。統計誤判個數N,其在總樣本n中所佔的比例稱為誤判率,表示如下:
(2)電能質量綜合評估體系
從(1)中可以看出,新型發電系統併網可能會造成頻率、電壓波動和閃變、諧波畸變等一系列問題,在這裡結合我國電能質量國家標準,選取頻率偏差指標、電壓偏差指標、三相不平衡指標、電壓波動指標、諧波畸變指標、電壓閃變指標這6項作為穩態電能質量綜合評估指標,建立的評估體系如圖1所示。
根據我國國家標準,這裡將電能質量等級劃分為5個級別,分別為優質、良好、中等、合格以及不合格。分別記為Q1,Q2,Q3,Q4,Q5,既避免了因分級太少而導致計算過程中偏差過大,從而影響計算結果的準確性;又避免了分級過多而造成的計算量過大。劃分結果如表1所示。其中x1代表頻率偏差,x2代表電壓總諧波畸變率,x3代表電壓波動(隨機不規則電壓波動),x4代表長時間閃變值,x5代表電壓偏差,x6代表電壓三相不平衡度。
表1電能質量等級極限值
Table.1 Limit values of each grade of power quality
(3)Fisher判別法樣本的獲取
根據電能質量的標準,各類電能質量的指標均有上下限值。當樣本中各項電能指標都落在某類電能質量所規定的範圍內,該樣本則屬於相應級別。故只要對標準類別進行有限次插值(或者在相應指標範圍內進行隨機取值)就可以獲得足夠多的訓練樣本,在這裡通過將每個等級範圍平均分為20等份來得到判別樣本。以Q1等級為例,平均插值得到的樣本表示如表2所示:
表2插值法得到的Q1樣本
Table.2 The samples of Grade Q1 by interpolation
(4)數據標準化
設被評估對象的6項電能質量指標經過c次測量,得到c×6個數據。其中每個數據用xij(1≤i≤c,1≤j≤6)來表示。由於不同指標量綱不同,為了消除不同指標之間的影響,在評估前需要對數據進行標準化處理。對於數值越小越好的逆向指標,做如下標準化處理:
式中,xij'表示進行標準化後得到的數據,xij表示測量方案所得的第i組數據中第j個指標值,xij max表示第j個指標的最大值。
類似的,對於數值越大越好的正向指標,處理方法如下:
(5)建立判別模型
對Q1、Q2、Q3、Q4等級內劃分得到的80個數據樣本,對其進行標準化處理,根據判別方法並結合SPSS(Statistical Product and Service Solutions)軟體,得到如表3所示的典則判別函數係數:
表3典則判別函數係數
Table.3 The coefficients of canonical discriminant function in SPSS
表4特徵值和貢獻率
Table.4 Eigenvalues and contribution rate
整理為:
y1=-118.089x1+61.002x2-87.632x3+157.729x4-9.824 (17)
y2=-96.062x1-66.892x2+89.462x3-110.55x4-1.542 (18)
y3=-4.144x1+43.66x2-26.543x3-8.835x4-0.954 (19)
Fisher判別分析中,判別方程的解釋量可以用其方差所佔的比例來解釋。結合表3和表4,可以看出,第一判別函數的方差貢獻率為70.8%,第二判別函數的方差貢獻率為28.2%,聯合運用這兩個函數進行判別時,判別結果的準確率可以達到99%,幾乎可以解釋所有樣本的信息。本發明採用前兩個判別函數即可。
將各類的均值向量帶入(17)-(18),得到的函數值則為兩個典則判別函數在各類別的中心值,如下表5所示:
表5判別函數中心值
Table.5 Center values of canonical discriminant function in each group
將插值法得到的所有樣本利用回判估計法帶入建立好的模型進行檢驗,經檢驗該模型的判斷正確率達到97.5%。只有第41、42組(原本屬於Q3等級)在歸類時被劃分到Q2組,與規定組別不符。這是因為這兩個誤判樣本位於第2組和第3組的交界處,比較容易發生誤判。
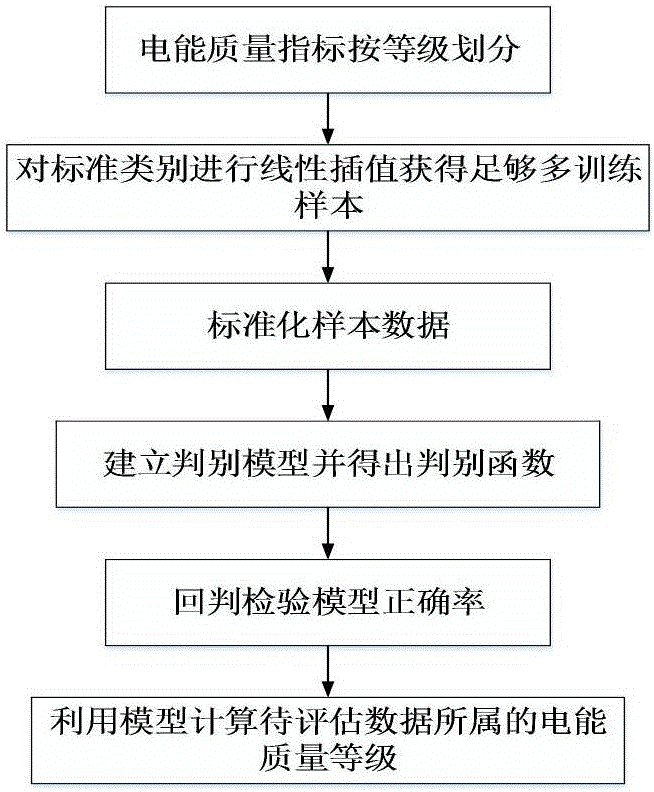
用Fisher法進行電能質量評估的流程圖如圖2所示。第一步,先將我國國家電能質量標準的六個指標劃分為Q1~Q5五個等級。第二步,為了得到Fisher判別模型,需要得到足夠多的訓練樣本數據,為此對標準類別進行線性插值。第三步,對所得樣本數據和待評估電能質量數據進行標準化處理,消除不同指標之間的量綱影響。第四步,利用處理後的樣本數據建立Fisher判別模型,並得出判別函數。最後,利用模型來判別待評估數據所處的電能質量等級,完成電能質量等級評估並得出結論。
利用本發明所提的方法對光伏併網系統的穩態電能質量進行綜合評估。採用Fluke 435II型電能質量分析儀為測量設備,對天津大學動模實驗室光伏併網耦合點的電能質量進行觀測並記錄,以探究光伏併網系統的電能質量等級,確定光伏併網可行性,加強對電能質量治理工作的指導。該測量實驗持續兩周,以24小時所得數據為一組,每3秒進行數據監測並記錄。對於得到的大量數據,採用科學的統計方法,以10分鐘為時間單元,求取一天內所測數據的95%概率大值作為數據典型值,最終形成的各指標代表性數據如表6所示。
表6測量指標數據的偏差值
Tab.6 The deviation value of data measured
為得出該併網光伏系統所屬的電能質量等級,同樣利用3.3.1的方法對表6的測量數據進行標準化,然後進行判別。將處理後的數據帶入式(17)和式(18),則判別函數計算值如下表7所示。然後根據判別原理,求取判別函數計算值與第1判別式和第2判別式中心的歐氏距離,選取距離最小的一組並將該組數據劃分到該組裡面。結果如表8內容所示。
表7待判數據的判別函數計算值
Table.7 The calculated values of discriminant functions
表8判別分析結果
Table.8 The results of discriminant analysis
通過表8內容可看出,在運用本發明所建立的Fisher判別模型對該光伏併網系統進行判別後,第1天到第7天所測量數據都與Q2等級的距離最為接近。由Fisher判別理論,可以得出該光伏系統屬於第2等級的結論,符合我國國家光伏併網要求,對當地電網電能質量的影響不大。
電能質量綜合評估是一個涉及多個指標的複雜問題,Fisher判別分析理論這一評價方法客觀合理,適用於電能質量的綜合評估。所採用的學習樣本採用線性插值的方法創建,每一等級狀態有20個學習樣本參與構造判別模型,此外模型具有較高的準確率。該方法不需要考慮不同指標之間的權重問題,從而避免了確定指標權重時由於方法選取不同而造成的評估結果差異。實際算例表面,利用所建立的模型對光伏併網系統穩態電能質量評估是合理可行的。不同運用場合下可以選取任意多的電能質量評估指標進行學習和模型建立。故該方法應用性廣泛,適用性強,具有比較大的推廣價值。
