一種碳纖維複合材料等效介電常數模型的構建方法與流程
2023-10-27 01:57:32 3
本發明涉及電磁環境與電磁兼容技術領域,尤其涉及一種碳纖維呈矩形排列情況下的碳纖維複合材料等效介電常數模型的構建方法。
背景技術:
碳纖維複合材料廣泛應用於飛機、衛星、汽車等行業領域,由於碳纖維的高電導率性能,碳纖維複合材料也經常替代貴重的金屬材料,用於結構體的電磁屏蔽性能。理論上現有的數值計算軟體能夠精確地計算複合材料的電磁特性如屏蔽效能、透射係數等,但是,碳纖維複合材料具有複雜的細觀幾何構型,需要考慮內部精細結構的網格剖分,往往產生巨大的未知數,導致無法求解。
為了有效解決複合材料電磁特性的求解難題,一般採用宏觀的等效介電常數來描述複合材料,從而能夠採用相同尺寸的等效介電常數模型來替代原有的細觀幾何模型。2015年公開的中國發明專利「非對稱人工電磁材料的等效電磁參數提取方法」(申請號:201510291977.8)採用數值迭代方法提取人工電磁材料的等效電磁參數,通過仿真大量的S參數進行反演,前期要求的數據量較大。2014年公開的中國發明專利「一種通孔型介質支撐等效介電常數計算方法」(申請號:201410422551.7)提出了等效介電常數的理論計算公式,2016年公開的中國發明專利「一種蜂窩吸波結構等效電磁參數的計算方法」(申請號:201610130516.7)採用強擾動理論計算蜂窩吸波結構等效電磁參數,這些方法只能應用於特定結構的複合材料。2012年第26卷第5期在《材料導報B:研究篇》公開的「纖維複合材料的電磁反射係數計算」只是針對單層碳纖維鋪設的材料等效電磁參數進行了研究。2016年第65卷第2期在《物理學報》公開的「高濃度纖維增強材料介電特性計算方法」提出了碳纖維增強複合材料的等效介電常數的解析公式,但是僅應用於碳纖維在橫截面按正方形排列的情況。
對於複合材料橫截面上碳纖維呈矩形排列的情況下,等效介電常數除了受到碳纖維和基體的電磁參數影響外,還受到結構參數的影響,無法用單一的理論公式計算得出。
技術實現要素:
本發明提供一種碳纖維複合材料等效介電常數模型的構建方法,採用半經驗表達式,利用少數的仿真計算即可建立碳纖維複合材料的等效介電常數模型,解決了實際數值仿真中碳纖維複合材料內部細觀幾何結構導致的網格剖分過多的難題,等效介電常數模型方便用於複合材料屏蔽效能、透波性能等數值仿真,計算簡單,便於實現,為複合材料的電磁屏蔽性能分析提供了有效手段。
為了達到上述目的,本發明提供一種碳纖維複合材料等效介電常數模型的構建方法,包含以下步驟:
步驟S1、針對橫截面上碳纖維呈矩形排列的複合材料,分別從碳纖維軸向和碳纖維徑向建立通用等效介電常數模型,該通用等效介電常數模型中包含未知參數;
步驟S2、根據傳輸線理論建立碳纖維複合材料的屏蔽效能表達式,該屏蔽效能表達式是碳纖維複合材料的通用等效介電常數模型中未知參數的函數;
步驟S3、通過仿真計算得到在與步驟S2中相同電磁波入射角度下的碳纖維複合材料上多個頻率點的實際屏蔽效能;
步驟S4、根據仿真計算得到的多個頻率點的實際屏蔽效能,結合碳纖維複合材料的屏蔽效能表達式,利用最小二乘法反演得到碳纖維複合材料的通用等效介電常數模型中的未知參數;
步驟S5、將計算得到的碳纖維複合材料的通用等效介電常數模型中的未知參數代入通用等效介電常數模型,完成碳纖維複合材料的通用等效介電常數模型的構建。
所述的步驟S1中,所述的從碳纖維軸向建立通用等效介電常數模型採用如下關係式:
ε軸向=vmεm+vfεf (1)
其中,ε軸向為軸向的通用等效介電常數;vm為基體材料的體積百分比;vf為碳纖維的體積百分比,一般取0%~20%;εm為基體材料的介電常數;εf為碳纖維的介電常數;
所述的從碳纖維徑向建立通用等效介電常數模型採用如下半經驗表達式:
其中,ε徑向為徑向的通用等效介電常數;s1為碳纖維的橫向間距;s2為碳纖維的縱向間距;d為碳纖維的直徑;λ為電磁波在複合材料中傳播的波長;a和b分別為未知參數;
其中,碳纖維複合材料中的基體材料和碳纖維的介電常數εm和εf都是複數形式。
所述的步驟S2中,所述的屏蔽效能表達式為:
S=-20lg(|Tl(a,b)×T0(a,b)|) (3)
其中,S為碳纖維複合材料的屏蔽效能;Tl(a,b)和T0(a,b)分別為在碳纖維複合材料兩個邊界面的透波係數,是未知參數a和b的函數。
所述的步驟S3中,所述的頻率點的數量大於等於3個。
所述的步驟S3中,所述的頻率點的選取需要滿足條件:在碳纖維複合材料的介電常數和碳纖維的體積百分比固定不變的條件下,選取多組不同的纖維間距,在每一組纖維間距下再選取至少三個頻率點,所述的纖維間距包含橫向間距和縱向間距。
所述的步驟S3中,所述的仿真計算是指:利用電磁仿真軟體建立描述實際碳纖維複合材料細觀幾何結構的模型,並進行數值求解得到在電磁波垂直入射條件下的屏蔽效能。
所述的步驟S4中,
所述的利用最小二乘法反演得到碳纖維複合材料的通用等效介電常數模型中的未知參數的步驟具體包含:
步驟S4.1、建立仿真的屏蔽效能向量:
SE(f)=[SE1(f),SE2(f),…,SEn(f)] (4)
其中,SE(f)為仿真的屏蔽效能向量;SEn(f)為在頻率f下的屏蔽效能;n為頻率點的個數;
步驟S4.2、建立屏蔽效能表達式的向量:
SC(f)=[S1,S2,…,Sn]
其中,SC(f)為計算的屏蔽效能表達式的向量;Sn為採用屏蔽效能表達式計算的屏蔽效能,為未知數a和b的函數;
步驟S4.3、建立最小值問題表達式:
步驟S4.4、利用最小二乘法求解最小值問題,得到通用等效介電常數模型中的未知參數。
本發明採用半經驗表達式,利用少數的仿真計算即可建立碳纖維複合材料的等效介電常數模型,解決了實際數值仿真中碳纖維複合材料內部細觀幾何結構導致的網格剖分過多的難題,等效介電常數模型方便用於複合材料屏蔽效能、透波性能等數值仿真,計算簡單,便於實現,為複合材料的電磁屏蔽性能分析提供了有效手段。
附圖說明
圖1是本發明提供的一種碳纖維複合材料等效介電常數模型的構建方法的流程圖。
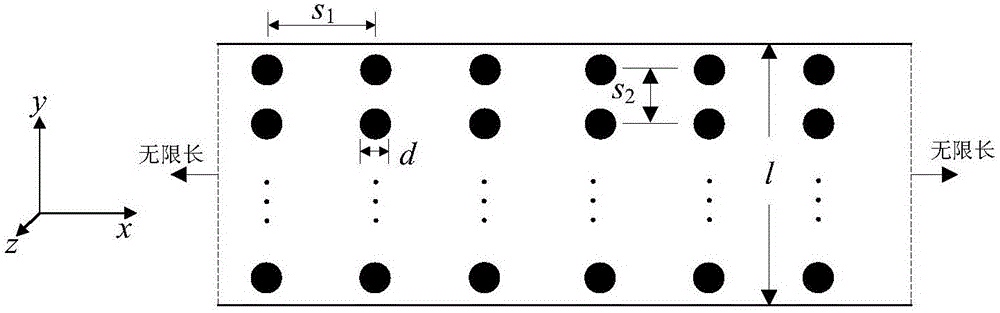
圖2是碳纖維複合材料的橫截面示意圖。
圖3是實施例中電磁波垂直入射碳纖維複合材料示意圖;
圖4是實施例中碳纖維複合材料屏蔽效能結果對比。
具體實施方式
以下根據圖1~圖4,具體說明本發明的較佳實施例。
如圖1所示,本發明提供一種碳纖維複合材料等效介電常數模型的構建方法,包含以下步驟:
步驟S1、針對橫截面上碳纖維呈矩形排列的複合材料,分別從碳纖維軸向和碳纖維徑向建立通用等效介電常數模型,該通用等效介電常數模型中包含未知參數;
所述的碳纖維複合材料為兩種材料複合,碳纖維設置在基體材料中,基體材料為基體相,碳纖維為增強相,內部的碳纖維相互平行不接觸,如圖2所示,碳纖維的橫向間距為s1,碳纖維的縱向間距為s2,碳纖維的直徑為d,碳纖維複合材料的厚度為l,碳纖維複合材料的長度無限長;
所述的從碳纖維軸向建立通用等效介電常數模型採用如下關係式:
ε軸向=vmεm+vfεf (1)
其中,ε軸向為軸向的通用等效介電常數;vm為基體材料的體積百分比;vf為碳纖維的體積百分比,一般取0%~20%;εm為基體材料的介電常數;εf為碳纖維的介電常數;
所述的從碳纖維徑向建立通用等效介電常數模型採用如下半經驗表達式:
其中,ε徑向為徑向的通用等效介電常數;s1為碳纖維的橫向間距;s2為碳纖維的縱向間距;d為碳纖維的直徑;λ為電磁波在複合材料中傳播的波長;a和b分別為未知參數;
其中,碳纖維複合材料中的基體材料和碳纖維的介電常數εm和εf都是複數形式;
步驟S2、根據傳輸線理論建立碳纖維複合材料的屏蔽效能表達式,該屏蔽效能表達式是碳纖維複合材料的通用等效介電常數模型中未知參數的函數;
S=-20lg(|Tl(a,b)×T0(a,b)|) (3)
其中,S為碳纖維複合材料的屏蔽效能;Tl(a,b)和T0(a,b)分別為在碳纖維複合材料兩個邊界面(與空氣接觸的上表面和下表面)的透波係數,是未知參數a和b的函數;
步驟S3、通過仿真計算得到在與步驟S2中相同電磁波入射角度下的碳纖維複合材料上多個頻率點的實際屏蔽效能;
本實施例中,步驟S2和步驟S3中的電磁波入射角度都可以選擇為垂直入射角度;
所述的頻率點的數量大於等於3個;
所述的頻率點的選取需要滿足條件:在碳纖維複合材料的介電常數和碳纖維的體積百分比固定不變的條件下,一般選取三組不同的纖維間距,在每一組纖維間距下選取三個頻率點(例如考慮1G~10GHz範圍,可以選取1GHz,2GHz,3GHz);
所述的仿真計算是指:利用電磁仿真軟體如HFSS建立描述實際碳纖維複合材料細觀幾何結構的模型,並進行數值求解得到在電磁波垂直入射條件下的屏蔽效能;
步驟S4、根據仿真計算得到的多個頻率點的實際屏蔽效能,結合碳纖維複合材料的屏蔽效能表達式,利用最小二乘法反演得到碳纖維複合材料的通用等效介電常數模型中的未知參數;
所述的利用最小二乘法反演得到碳纖維複合材料的通用等效介電常數模型中的未知參數的步驟具體包含:
步驟S4.1、建立仿真的屏蔽效能向量:
SE(f)=[SE1(f),SE2(f),…,SEn(f)] (4)
其中,SE(f)為仿真的屏蔽效能向量;SEn(f)為在頻率f下的屏蔽效能,n為頻率點的個數,在本實施例中,n取值為組數的3倍,一般取值為9
步驟S4.2、建立屏蔽效能表達式的向量:
SC(f)=[S1,S2,…,Sn]
其中,SC(f)為計算的屏蔽效能表達式的向量;Sn為採用屏蔽效能表達式計算的屏蔽效能,為未知數a和b的函數;
步驟S4.3、建立最小值問題表達式:
步驟S4.4、利用最小二乘法求解最小值問題,得到通用等效介電常數模型中的未知參數;
較佳地,可以利用MATLAB中的lsqnonlin函數(該函數採用非線性最小二乘方法求解)求最小值來得到等效介電常數模型中的未知參數;
步驟S5、將計算得到的碳纖維複合材料的通用等效介電常數模型中的未知參數代入通用等效介電常數模型,完成碳纖維複合材料的通用等效介電常數模型的構建。
在本發明的一個實施例中,按照本發明提供的方法進行碳纖維複合材料的通用等效介電常數模型的構建:
某碳纖維複合材料平板用於屏蔽外部的高強度輻射場,厚度l=2mm,纖維直徑d=0.1mm,基體材料的介電常數εm=3.5ε0(ε0為空氣介電常數),碳纖維的介電常數εf=ε0-j4000/(2πf),根據碳纖維的橫向間距和縱向間距進行三組取值:A組(橫向間距s1=0.12mm,縱向間距s2=1/3mm),B組(橫向間距s1=0.2mm,縱向間距s2=1/5mm),C組(橫向間距s1=0.32mm,縱向間距s2=1/8mm)。
步驟S1、根據式(1)可以得到碳纖維軸向的介電常數ε軸向,根據式(2)可以得到碳纖維軸向的介電常數ε徑向,其為未知參數a和b的函數。
步驟S2、如圖3所示,電磁波垂直入射條件下,且入射電場與碳纖維軸向垂直,根據式(3)計算複合材料的屏蔽效能,得到S的表達式,其仍為未知參數a和b的函數。
步驟S3、分別選取A組、B組和C組碳纖維間距下的2GHz、4GHz和6GHz的三個頻率點,在電磁仿真軟體HFSS中建立描述實際碳纖維複合材料細觀幾何結構的模型,並進行電磁求解;
三組頻率點的屏蔽效能分別為:
A組:S1(f)=0.103dB(2GHz)、S2(f)=0.225dB(4GHz)、S3(f)=0.453dB(6GHz)。
B組:S4(f)=0.033dB(2GHz)、S5(f)=0.120dB(4GHz)、S6(f)=0.274dB(6GHz)。
C組:S7(f)=0.025dB(2GHz)、S8(f)=0.102dB(4GHz)、S9(f)=0.223dB(6GHz)。
步驟S4、屏蔽效能向量為:
SE(f)=[S1(f),S2(f),S3(f),S4(f),S5(f),S6(f),S7(f),S8(f),S9(f)] (5)
利用最小二乘法求解得到未知參數a=-3.9,b=0.9。
步驟S5、未知參數將a=-3.9,b=0.9代入式(2)即完成通用等效介電常數模型的構建,等效介電常數模型的厚度仍為l,模型的參數用ε軸向和ε徑向表示。
利用構建的等效介電常數模型,採用傳輸線理論計算了1.5GHz~20GHz範圍內的屏蔽效能,並與實際碳纖維複合材料細觀幾何結構模型的HFSS仿真結果進行了對比,如圖4所示,A組、B組、C組的結果都吻合較好,構建的等效介電常數模型能夠很好地描述碳纖維複合材料的介電特性。
本發明的優點在於:
1、採用了半經驗表達式,利用少量的先驗數據,能準確地描述碳纖維複合材料的等效介電常數;
2、直接採用屏蔽效能來反演構建複合材料的等效介電常數模型,方便簡單,屏蔽效能的計算採用一般的商用電磁仿真數值軟體如HFSS、FEKO等都可以實現;
3、在電磁波垂直照射條件下,建立的等效介電常數模型也可以採用解析公式求得屏蔽效能、反射係數、透射係數等電磁特性,不需要開展複雜的數值計算;
4、建立的等效介電常數模型可以替代原有的複合材料細觀幾何模型,避免了纖細的碳纖維的網格剖分,降低了電磁特性數值仿真的網格數和計算內存,為複合材料的電磁屏蔽性能分析提供有效手段。
儘管本發明的內容已經通過上述優選實施例作了詳細介紹,但應當認識到上述的描述不應被認為是對本發明的限制。在本領域技術人員閱讀了上述內容後,對於本發明的多種修改和替代都將是顯而易見的。因此,本發明的保護範圍應由所附的權利要求來限定。
