一種低複雜度的(47,24,11)平方剩餘碼解碼方法與流程
2023-10-19 06:28:07 2
本發明涉及信道糾錯碼領域,更具體的說涉及一種適用於循環碼的解碼方法,其可應用(47,24,11)平方剩餘碼。
背景技術:
作為可靠性傳輸的重要保證,自1948年香農於「通信的數學原理」這一開創性的論文中提出信道編碼定理以來,信道糾錯碼一直都受到學者們的廣泛關注。循環碼是最重要的糾錯碼之一,包括Golay碼、Hamming碼、Bose Chaudhuri Hocquenghem(BCH)碼、平方剩餘碼等。(47,24,11)平方剩餘碼是其中一個重要的碼型,但由於受限於複雜的解碼算法,該碼型一直未能在實際應用中應用。本發明基於循環碼的伽羅華域特性,提出一種低複雜度的(47,24,11)平方剩餘碼解碼算法。
技術實現要素:
本發明的主要目的在於提供一種糾錯能力為5的(47,24,11)平方剩餘碼解碼算法,其可應用於(47,24,11)平方剩餘碼解碼上,可以有效降低(47,24,11)平方剩餘碼在產品中的複雜度。
為了達成上述目的,本發明提供的方法是
一種低複雜度的(47,24,11)平方剩餘碼解碼方法,其特徵在於:令生成多項式為g=(11110111011011100011000),1≤i≤46;0≤j≤46;接收碼字為r=(r0,r1,…,r46),解碼的步驟包括,
步驟1:計算校正子s=rp+r23g(23)+r24g(24)+…+r46g(46),其中rp=(r0,r1,…,r22)和rm=(r23,r24,…,r46)。
步驟2:如果校正子的重量,即校正子s中1的數量,w(s)≤5,則錯誤模式為e=(s|01×(n-k));此時,糾正後的接收碼字為c′=r+e,解碼成功。
步驟3:如果w(s)>5,意味著至少有1個錯誤發生在rm;此時依次將rm中 的一個比特ri取反,並重新計算校正子s+=g(i)。如果w(s)≤4,則錯誤模式為e=(s|01×(n-k))+1i;此時,糾正後的接收碼字為c′=r+e,解碼成功。
步驟4:如果w(s)>4,表示至少有兩個錯誤發生在rm;此時依次將rm中的兩個比特ri和rj取反,並重新計算校正子s=s+g(i)+g(j)。如果w(s)≤3,則錯誤模式為e=(s|01×(n-k))+1i+1j;此時,糾正後的接收碼字為c′=r+e,解碼成功。
一種低複雜度的(47,24,11)平方剩餘碼解碼方法,其特徵在於:如果w(s)>3,則意味著最多兩個錯誤發生在rp;此時將接收碼字左移或右移23比特,獲取一個移位後接收碼字,對於移位後接收碼字存在兩種情況:1)最多兩個錯誤發生在rm;2)三個錯誤發生在rm,其中一個發生在r23;此時解碼步驟包括,
步驟1:計算移位後接收碼字校正子s=rp+r23g(23)+r24g(24)+…+r46g(46),其中rp=(r0,r1,…,r22)和rm=(r23,r24,…,r46)。
步驟2:如果校正子的重量,即校正子s中1的數量,w(s)≤5,則錯誤模式為e=(s|01×(n-k));此時,糾正後的接收碼字為c′=r+e;如果接收碼字左(右)移23比特,則糾正後的接收碼字右(左)移23比特,解碼成功。
步驟3:如果w(s)>5,意味著至少有1個錯誤發生在rm;此時依次將rm中的一個比特ri取反,並重新計算校正子s+=g(i)。如果w(s)≤4,則錯誤模式為e=(s|01×(n-k))+1i;此時,糾正後的接收碼字為c′=r+e;如果接收碼字左(右)移23比特,則糾正後的接收碼字右(左)移23比特,解碼成功。
步驟4:如果w(s)>4,表示至少有兩個錯誤發生在rm;此時依次將rm中的兩個比特ri和rj取反,並重新計算校正子s=s+g(i)+g(j)。如果w(s)≤3,則錯誤模式為e=(s|01×(n-k))+1i+1j;此時,糾正後的接收碼字為c′=r+e;如果接收碼字左(右)移23比特,則糾正後的接收碼字右(左)移23比特,解碼成功。
步驟5:如果w(s)>3,此時依次將rm中的三個比特r23、ri和rj取反,並 重新計算校正子s=s+g(23)+g(i)+g(j)。如果w(s)≤2,則錯誤模式為e=(s|01×(n-k))+123+1i+1j;此時,糾正後的接收碼字為c′=r+e;如果接收碼字左(右)移23比特,則糾正後的接收碼字右(左)移23比特,解碼成功。
一種低複雜度的(47,24,11)平方剩餘碼解碼方法,其特徵在於:g(i)的計算步驟為,
步驟1:g(i-1)>>1為將g(i-1)右移1比特;
步驟2:表示g(i-1)的第22比特;如果為1,則g(i)=(g(i-1)>>1)+g;如果為0,則g(i)=(g(i-1)>>1)。
附圖說明
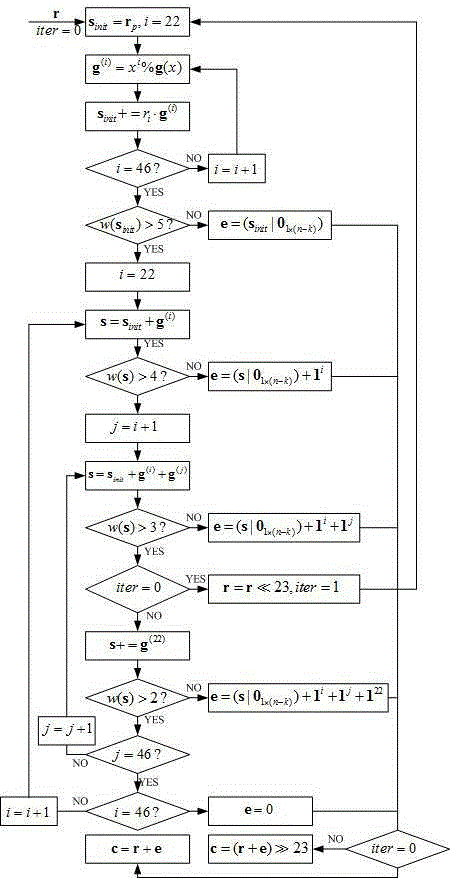
附圖1為低複雜度的(47,24,11)平方剩餘碼解碼流程圖。
具體實施方法
上述功能實現的技術方案結合附圖進行進一步的描述如下:
根據圖1所示的低複雜度的(47,24,11)平方剩餘碼解碼流程圖,其特徵在於:
步驟1:令生成多項式為g=(11110111011011100011000),1≤i≤46;g(i-1)>>1為將g(i-1)右移1比特;表示g(i-1)的第22比特;如果為1,則g(i)=(g(i-1)>>1)+g;如果為0,則g(i)=(g(i-1)>>1);0≤j≤46;接收碼字為r=(r0,r1,…,r46),iter=0。
步驟2:計算校正子s=rp+r23g(23)+r24g(24)+…+r46g(46),其中rp=(r0,r1,…,r22)表示信息部分,rm=(r23,r24,…,r46)表示校驗部分;
步驟3:如果校正子的重量,即校正子s中1的數量,w(s)≤5,則錯誤模式為e=(s|01×(n-k));此時,進入步驟8。
步驟4:如果w(s)>5,意味著至少有1個錯誤發生在rm;此時依次將rm中 的一個比特ri取反,並重新計算校正子s+=g(i)。如果w(s)≤4,則錯誤模式為e=(s|01×(n-k))+1i;此時,進入步驟8。
步驟5:如果w(s)>4,表示至少有兩個錯誤發生在rm;此時依次將rm中的兩個比特ri和rj取反,並重新計算校正子s=s+g(i)+g(j)。如果w(s)≤3,則錯誤模式為e=(s|01×(n-k))+1i+1j;此時,進入步驟8。
步驟6:如果w(s)>3且iter=1,此時依次將rm中的三個比特r23、ri和rj取反,並重新計算校正子s=s+g(23)+g(i)+g(j)。如果w(s)≤2,則錯誤模式為e=(s|01×(n-k))+123+1i+1j;此時,進入步驟8。
步驟7:如果w(s)>3且iter=0,則意味著最多兩個錯誤發生在rp;此時將接收碼字左移或右移23比特,獲取一個移位後接收碼字,對於移位後接收碼字存在兩種情況:1)最多兩個錯誤發生在rm;2)三個錯誤發生在rm,其中一個發生在r23;此時,進入步驟2。
步驟8:糾正後的接收碼字為c′=r+e;如果iter=1,表示接收碼字左(右)移23比特,則將糾正後的接收碼字右(左)移23比特,解碼成功。
使用實例:
實例1:
令發送碼字為,c=(00110100000100101001110011110101111001000000000);
令接收碼字為,r=(11110100000100101001111101110101111001000000000);
令錯誤模式為,e=(11000000000000000000001110000000000000000000000);
我們發現總共發生5個錯誤,其中2個在信息部分,3個在校驗部分,具體的解碼步驟如下述:
1.計算校正子:
s=(01001100110110010010101)。因為w(s)=11>5,進入步驟4。
2.因為所有的w(s)>4,進入步驟5。
3.當i=23,j=24,則s=(11000000000000000000001)。因為w(s)=3≤3,則e=(11000000000000000000001110000000000000000000000),進入步驟8。
4.因為iter=0,此時解碼後的接收碼字為:
c′=r+e=(00110100000100101001110011110101111001000000000)。解碼成功。
實例2:
令發送碼字為,
c=(00101000111010110110111011110000110010000000000)。
令接收碼字為,
r=(11101000111010110110111101110000110010000000001)
令錯誤模式為,
e=(11000000000000000000000110000000000000000000001)
我們發現總共發生5個錯誤,其中3個在信息部分,2個在校驗部分,具體的解碼步驟如下述:
1.計算校正子:
s=(10100010000001010100101)。因為w(s)=8>5,進入步驟4。
2.因為所有的w(s)>4,進入步驟5。
3.因為所有的w(s)>3,進入步驟7。
4.因為w(s)>3且iter=0,意味著最多2個錯誤發生在rp;根據循環碼的定義,將接收碼字循環移位23個比特,獲取新的接收碼字,
r=(10111000011001000000000111101000111010110110111)。設置iter=1,進入步驟2。
5.計算新接收碼字的校正子:
s=(01110001000000101010010)。因為w(s)=8>5,進入步驟4。
6.因為所有的w(s)>4,進入步驟5。
7.因為所有的w(s)>3,進入步驟6。
8.當i=24,j=25,thens=(11000000000000000000000)。因為w(s)=2≤2,then e=(11000000000000000000000111000000000000000000000),進入步驟8。
9.有c′=r+e=(01111000011001000000000000101000111010110110111)。因為iter=1,向右循環移位c′23比特,獲取c′=(00101000111010110110111011110000110010000000000),此時解碼成功。
本領域普通技術人員可以理解,實現上述實施例中的全部或部分步驟是可以通過程序來指令相關的硬體來完成,所述的程序可以在存儲於計算機可讀取存儲介質中,所述的存儲介質,如ROM/RAM、磁碟、光碟等。
以上所述僅為本發明的較佳實施例而已,並不用以限制本發明,凡在本發明的精神和原則之內所作的任何修改、等同替換和改進等,均應包含在本發明的保護範圍之內。
