基於共享直線段的平面片束排序方法和系統與流程
2023-10-08 12:22:24 2
本發明實施例屬於軟體領域,尤其涉及一種基於共享直線段的平面片束排序方法和系統。
背景技術:
在二維空間中,通過1維基元來構造2維基元(多邊形)的研究已經較多。其最早出現於雙重獨立地圖編碼(DIME,Dual Independent Map Encoding)格式(Peucker,T.K.et al.(1975).Cartographic Data Structure[J].The Ameircan Cartographer,2(1):55-69;Meixler,D.et al.(1987).Polygonization and Topological Editing at the Bureau of the Census[C].AUTO-CARTO 8Proceedings:731-738.)和拓撲整合地理編碼與參考(TIGER,Topologically Integrated Geographic Encoding and Referencing)格式(Peuquest,D.J.(1984).A Conceptual Framework and Comparison of Spatial Data Models[J].Cartographica:The International Journal of Geographic Information and Geovisualization,21(4):66-113;Hodgson,M.E.et al.(1989).Cartographic Data Capture using CAD[C].AUTO-CARTO 9Proceedings:406-415.)的二維數據的多邊形化過程之中。前者是通過1維直線段構造2維多邊形,後者是通過1維鏈(直線段的集合)來構造2維多邊形。直線段是1維基元,鏈也是1維基元,以上多邊形化算法的核心在於通過1維基元與1維基元之間的夾角計算來尋找構造每個多邊形的所有相關1維基元(直線段或鏈),以上這些針對國外格式二維空間數據提出二維多邊形化算法的計算夾角方式,與我國學者提出的左轉(或右轉)算法(陳春等.(1996).GIS中多邊形圖拓撲信息生成的數學基礎[J].測繪學報,25(4):266-271;杜清運.(1989).地圖資料庫中多邊形數據的自動組織[J].測繪學報,18(3):204-212.)很類似。除此之外,二維多邊形化算法還包括:
-Qi算法(齊華等.(1996).建立結點上弧-弧拓撲關係的Qi算法[J].測繪學報,25(3):233-235;齊華.(1997).自動建立多邊形拓撲關係算法步驟的優化與改進[J].測繪學報,26(3):254-260;齊華,李德仁.(2005).基於Qi(xi,yi)函數的輻射線空間分割與TIN的約束邊鑲嵌[J].武漢大學學報(信息科學版),30(3):204-208;齊華,李德仁,朱慶.(2003).確定射線空間相鄰關係的兩個非角度算法的時間複雜度分析[J].武漢大學學報(信息科學版),28(5):611-614)。
-方位角算法(閆浩文等.(2000).基於方位角計算的拓撲多邊形自動構建快速算法[J].中國圖象圖形學報,5A(7):563-567;閆浩文,王家耀.(2009).地圖群組目標描述與自動綜合[M].北京:科學出版社;閆浩文等.(2007).計算機地圖製圖原理與算法基礎[M].北京:科學出版社;閆浩文,王明孝等.(2012).計算幾何:空間數據處理算法[M].北京:科學出版社.)。
-矢量外積法(高雲瓊等.(2002).同一結點上弧-弧拓撲關係生成的新算法[J].計算機應用研究,(4):58-59;),
它們的側重點在於從當前1維基元尋找最鄰近1維基元時不再使用夾角值,而且分別藉助Qi函數、方位角、矢量積與二叉排序樹。以上文獻的不同之處在於,針對從1維基元矢量的集合(一種比率尺度數據)推導出1維基元與1維基元之間的排序順序(一種定序尺度數據),所採用的計算策略有所不同,從而造成算法的空間(時間)複雜度有所區別,但本質上都是針對基於0維共享節點的1維基元集合的排序。
在三維空間中,如何構造有效的3維基元(也稱多面體化)遠遠沒有以上二維空間中多邊形的構造算法(如上所述稱為多邊形化)成熟,包括ISO19107'Spatial Schema'(ISO.(2003).ISO/TC 211,ISO International Standard19107:2003,Geographic Information-Spatial Schema.)中存在對於「體」的抽象定義(即GM_Solid和TP_Solid),GML和CityGML中沿用ISO 19107中對於「體」的定義(即gml:Solid)(Protele,C.OpenGIS Geography Markup Language(GML) Encoding Standard,Copyright Open Geospatial Consortium,Inc.,v3.2.1;Groger,G.et al.OGC City Geography Markup Language(CityGML)Encoding Standard,Open Geospatial Consortium,Inc.,v2.0),以上在三維形式化數據結構(3D Formal Data Structure)(Molenaar,M.(1990).A Formal Data Structure for 3D Vector Maps[C].In:Proceedings of EGIS'90,2.Amsterdam,the Netherlands:770-781.)、簡化空間模型(SSM,Simplified Spatial model)(Zlatanova,S.(2000).3D GIS for Urban Development[D].Ph.D Dissertation,The Netherlands,ITC.)、城市數據模型(UDM,Urban Data Model)(Coors,V.(2003).3D-GIS in Networking Environments.Computers,Environment and Urban Systems,27:345-357.)、面向對象的三維數據模型(Object-oriented 3D Data Model)(Shi,W.Z.,Yang,B.S.,Li,Q.Q.(2003).An Object-oriented Data Modle for Complex Objects in Three-dimensional Geographical Information Systems[J].International Journal of Geographical Information Science,17(5):411-430.)等各種三維空間數據模型(Zlatanova,S et al.(2004).Topological Models and Frameworks for 3D Spatial Objects[J].Computers&Geosciences,30:419-428;)中都存在3維體對象,但它們均沒有顯式說明一個有效的3維對象從何而來。
與之對比的,郭仁忠等提出了一種「面向地籍的三維空間數據模型」並給出了其中0維點、1維線、2維面和3維體的明確基元定義,以及基元與基元之間拓撲關係的完整羅列(Guo,R.Z.et al.(2012).Logical Design and Implementation of the Data Model for 3D Cadastre in China[C].3rd International Workshop on 3D Cadastres:Developments and Practices,Shenzhen,China:113-136;),論述了要實現3維產權體的構建不能跨維(換言之,無法通過1維線基元構造3維產權實體,否則會產生二義性),必須基於2維平面片集合構造有效的3維產權體(郭仁忠等.(2010).三維地籍形態分析與數據表達[J].中國土地科學,24(12):45-51;郭仁忠等.(2012).基於面片集合的三維地籍產權體的拓撲自動構建[J].測繪學報,41(4):620-626;Ying,S.et al.(2014).Construction of 3D Volumetric Objects for a3D Cadastral System[J].Transactions in GIS,22p.),這裡的「有效的3維產權體」指的是生成的3維產權體不存在疊置也沒有縫隙;同時,3維產權體是一個二維流形(2-manifold),即表面上的任何一點的領域都與一個小圓盤是拓撲等價的,或稱同胚於二維流形。以上通過2維面片構建3維產權體的基本原理是:尋找構造3維實體包含的所有相關2維平面片,其關鍵在於基於共享直線段的平面束排序,該方法能夠保證3維產權體與3維產權體之間拓撲關係的一致性(賀彪等.(2011).顧及外拓撲的異構建築三維拓撲重建[J].武漢大學學報(信息科學版),36(5):579-583;李霖等.(2012).空間體對象間三維拓撲構建研究[J].武漢大學學報(信息科學版),37(6):719-723;)。特別的,虞昌彬和郭仁忠等還闡述了一種基於統一邏輯的空間實體構造方法(即Automatic Construction of Spatial Entities Based on Unified Logic,簡寫為ACSEBUL方法),該方法不僅可以應用於通過1維邊/鏈拓撲自動構建2維多邊形,而且可以應用於通過2維平面片拓撲自動構建3維體,而且以上兩者在邏輯上是統一的(Guo,R.Z.,Yu Changbin et al.(2015).ACSEBUL:An Approach for the Construction of Spatial Entities Based on Unified Logic[J].Transactions in GIS,29;虞昌彬.(2015).三維地籍產權體幾何表達、構造與可視化[D].博士學位論文,武漢:武漢大學;虞昌彬等.(2015).一種地理空間實體構建方法及系統[P].國家發明專利授權號ZL2014103099061,申請日期2014年6月30日,授權日期2015年3月25日.)。
儘管如此,以上關於「面向地籍的三維空間數據模型」一系列相關研究與文獻目前只闡述了該關鍵步驟(即基於共享直線段的平面束排序)的基本思想和原理,尚未給出該關鍵步驟的形式化,尤其是以上步驟的數值計算過程的形式化描述與分析。即,目前還沒有有效的3維基元構造算法,故有必要提出一種新的技術方案以解決上述問題。
技術實現要素:
本發明實施例提供了一種基於共享直線段的平面片束排序方法和系統,旨在解決現有的方法沒有有效的3維基元構造算法的問題。
本發明實施例的第一方面,提供了一種基於共享直線段的平面片束排序方法,所述方法包括:
確定三維實體包含的二維平面;
確定所述二維平面的表徵矢量;
根據所述二維平面的表徵矢量將對應的二維平面投影至XOY平面;
將預設的起始平面變換為X軸正向,且所述起始平面的法向量變換為X軸正向朝上,所述預設的起始平面為所述三維實體包含的二維平面中的任一個二維平面,所述預設的起始平面的表徵矢量為起始表徵矢量;
在XOY平面上,計算起始表徵矢量與確定的其他表徵矢量的夾角,並根據夾角的大小確定對應的二維平面與預設的起始平面的遠近。
本發明實施例的第二方面,提供了一種基於共享直線段的平面片束排序系統,所述系統包括:
二維平面確定單元,用於確定三維實體包含的二維平面;
表徵矢量確定單元,用於確定所述二維平面的表徵矢量;
平面投影單元,用於根據所述二維平面的表徵矢量將對應的二維平面投影至XOY平面;
起始平面變換單元,用於將預設的起始平面變換為X軸正向,且所述起始平面的法向量變換為X軸正向朝上,所述預設的起始平面為所述三維實體包含的二維平面中的任一個二維平面,所述預設的起始平面的表徵矢量為起始表徵矢量;
表徵矢量的夾角計算單元,用於在XOY平面上,計算起始表徵矢量與確定的其他表徵矢量的夾角,並根據夾角的大小確定對應的二維平面與預設的起始平面的遠近。
在本發明實施例中,由於將三維實體包含的二維平面都投影至XOY平面,因此,在XOY平面上,計算的起始表徵矢量與確定的其他表徵矢量的夾角的大小即表示該其他表徵矢量對應的二維平面與預設的起始平面的遠近,從而能夠確定三維實體包含的各個二維平面的遠近關係,進而實現三維實體的構造。
附圖說明
圖1是本發明第一實施例提供的ISO 19017'Spatial Schema'中涉及的邊界包(boundary package)與共邊界包(co-boundary package)的示意圖;
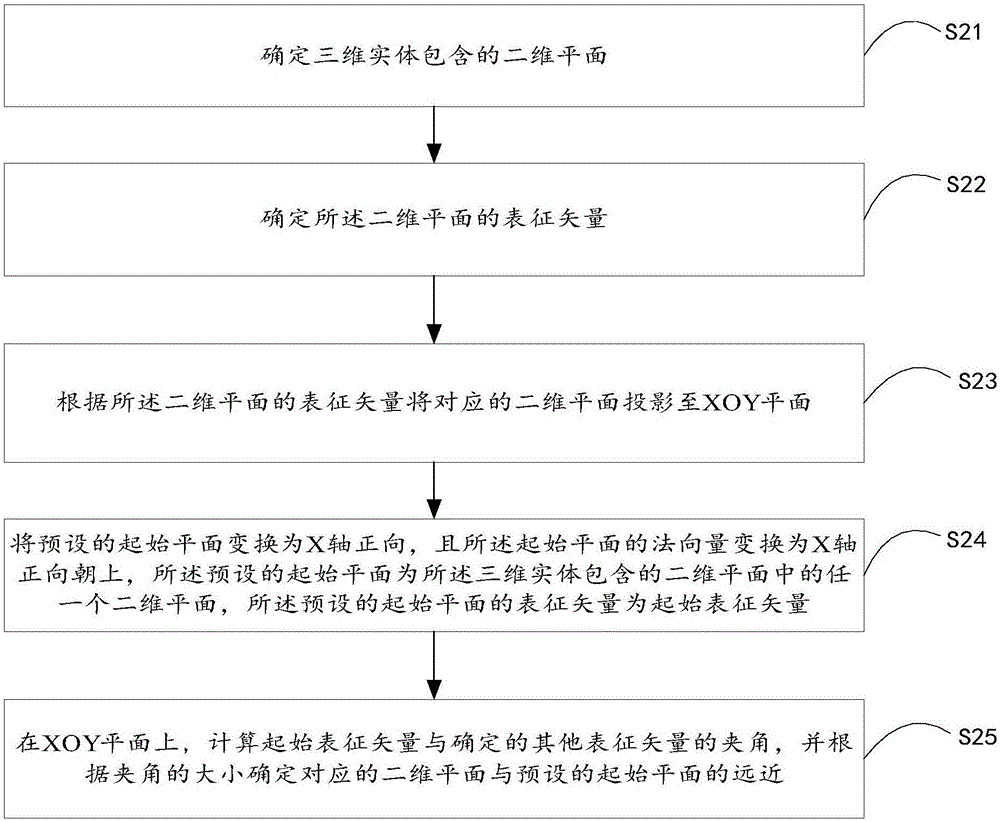
圖2是本發明第一實施例提供的一種基於共享直線段的平面片束排序方法的流程圖;
圖3(a)是本發明第一實施例提供的繞Z軸在XOY平面內轉的示意圖;
圖3(b)是本發明第一實施例提供的繞X軸在YOZ平面內轉的示意圖;
圖3(c)是本發明第一實施例提供的繞Y軸在ZOX平面內轉的示意圖;
圖4是本發明第一實施例提供的一種總體技術流程圖;
圖5(a)是本發明第一實施例提供的一種嵌入於任何三維空間的示意圖;
圖5(b)是本發明第一實施例提供的一種垂直於XOY平面的示意圖;
圖5(c)是本發明第一實施例提供的一種平面片簡化為直線段的示意圖;
圖6(a)是本發明第一實施例提供的一種AB在f1和f2中的環繞方向相同的示意圖;
圖6(b)是本發明第一實施例提供的一種AB在f1和f2中的環繞方向相異的示意圖;
圖7(a)是本發明第一實施例提供的一種初始平面片集合的示意圖;
圖7(b)是本發明第一實施例提供的一種基於分享直線段的平面束的示意圖;
圖7(c)是本發明第一實施例提供的一種將三維平面束轉換至二維直線段束的示意圖;
圖8是本發明第二實施例提供的一種基於共享直線段的平面片束排序系統的示意性框圖。
具體實施方式
為了使本發明的目的、技術方案及優點更加清楚明白,以下結合附圖及實施例,對本發明進行進一步詳細說明。應當理解,此處所描述的具體實施例僅僅用以解釋本發明,並不用於限定本發明。
本發明第一實施例中,確定三維實體包含的二維平面,確定所述二維平面的表徵矢量,根據所述二維平面的表徵矢量將對應的二維平面投影至XOY平面,將預設的起始平面變換為X軸正向,且所述起始平面的法向量變換為X軸正向朝上,所述預設的起始平面為所述三維實體包含的二維平面中的任一個二維平面,所述預設的起始平面的表徵矢量為起始表徵矢量,在XOY平面上,計算起始表徵矢量與確定的其他表徵矢量的夾角,並根據夾角的大小確定對應的二維平面與預設的起始平面的遠近。
為了說明本發明所述的技術方案,下面通過具體實施例來進行說明。
實施例一:
由於關於「面向地籍的三維空間數據模型」一系列相關研究與文獻目前只闡述了該關鍵步驟(即基於共享直線段的平面束排序)的基本思想和原理,尚未給出該關鍵步驟的形式化,尤其是以上步驟的數值計算過程的形式化描述與分析。以上步驟的形式化表達(尤其是其數值計算過程的形式化表達,典型的給予計算公式的形式化表達)有助於:
(1)首先,希望這成為地理信息科學領域(特別是三維空間數據組織這一小領域)的基礎性知識(就像「如何通過三個點確定一個平面」或「如何通過四個點確定一個圓」的形式化計算公式是數學領域中的基礎性知識一般),這些基礎性知識作為奠基非常重要;
(2)同時,方便相關領域的初學者直接調用與學習,方便他們「依葫蘆畫瓢」(即直接照著形式化的數學計算公式去進一步實現);
(3)同時,為後來相關領域研究者提供直接的參考與調用,也即方便後來者在此基礎上快速實現有效的3維實體構建並把更多的研究精力花費在後續研究之中。
出於以上三點考慮,這裡認為本發明具有極其重要的基礎理論研究價值。
為了更為清晰地闡述本發明實施例提供的基於共享直線段的平面片束排序方法,這裡借用ISO 19107'Spatial Schema'邊界(Boundary)和共邊界(Coboundary)包來說明(如附圖1所示):在二維空間中,為了封閉一個多邊形,需要找到構造該多邊形的所有相關邊(即找到TP_Face包含的TP_DirectedEdge集合,如線條所圍的區域1);如何判斷邊與邊是否相關,關鍵在於從基於節點的邊束中找到從起始邊出發的第一條邊和最後一條邊,其本質是基於共享節點的邊束排序(即基於TP_Node的TP_DirectedEdge集合排序,如區域3)。相對的,在三維空間中,為了封閉一個體,需要找到構造該體的所有相關平面片(即找到TP_Solid包含的TP_DirectedFace集合,如區域2)。如何判斷平面片與平面片是否相關,關鍵在於從基於共享直線段平面束中找到從起始平面片出發的第一個平面片和最後一個平面片,其本質是基於共享直線段的平面束排序(即基於TP_Edge的TP_DirectedFace集合排序,如區域4)。本發明著重於區域4的數值計算過程的形式化表達,事實上區域4的具體實現包含了區域3。
更為具體的,要實現「三維實體的構造方法」,主要在於實現「基於共享直線段的平面束排序」,其數值計算過程包括如下步驟:(1)計算平面片的表徵矢量;(2)計算旋轉方位角及旋轉矩陣;(3)比較幾何變換後的平面片表徵矢量,後面詳述。
圖2示出了本發明第一實施例提供的一種基於共享直線段的平面片束排序方法的流程圖,詳述如下:
步驟S21,確定三維實體包含的二維平面。
具體地,尋找三維實體包含的所有相關的二維平面(或稱平面片,簡稱平面)。
步驟S22,確定所述二維平面的表徵矢量。
可選地,所述步驟S22具體包括:
A1、確定所述二維平面的法向量和環繞方向。
A2、叉乘所述二維平面的法向量和環繞方向,叉乘的結果為所述二維平面的表徵矢量。
具體地,多個平面可能相交於多條共享直線段,可以選取其中任意一條進行排序,排序結果一致。設其中一條共享直線段為Seg或Seg(sPt,ePt),其中,sPt為該共享直線段本身的起點,ePt為該共享直線段本身的終點,該共享直線段本身方向始終由sPt指向ePt,該方向也稱「物理方向」(標記為SegV)。
值得注意的是,該共享直線段同時在每個相接平面中也有一個方向,稱「環繞方向」(標記為rSegV),該方向始終保持與形成該平面法向量的直線段環繞方向一致(即符合右手定則,四指方向為構成該平面的直線段依次排列方向,大拇指指向該平面的法向量)。具體的,將共享直線段(Seg)在某一相接平面內遵循右手定則形成的有向直線段稱為「環繞直線段」(標記為rSeg),由「環繞直線段」的起點指向終點所形成的矢量稱「環繞方向」(標記為rSegV)。針對指定的共享直線段,其在某一平面內的「環繞方向」與本身「物理方向」或相同或相反。
針對平面束(多個二維平面)中的每個平面(標記為facet),由環繞直線段的終點往起點的視角望去,該平面簡化為一條直線段,記為「表徵直線段」(標記為ResSeg)。由表徵直線段的起點指向終點所形成的矢量,稱為「表徵矢量」(標記為ResSegV)。該表徵矢量可以由該平面片的法向量(標記為facet.normal)與直線段在該平面內的環繞方向(rSegV)通過矢量叉乘得到。在叉乘時,之所以採用共享直線段在該平面內的「環繞方向」而非共享直線段的本身「物理方向」,是為了保證叉乘結果能夠代表該平面片。
步驟S23,根據所述二維平面的表徵矢量將對應的二維平面投影至XOY平面。
由於平面束仍然位於三維空間中,也即表徵直線段仍然位於統一的三維平面內。為數值計算方便,需要將所有表徵直線段轉移至統一的二維平面內,從而方便藉助表徵直線段的排序來代表相應平面片的排序。此時,需要藉助保持拓撲性質不變的三維幾何變換。值得注意的是,表徵直線段之間的排序結果(即相對位置)是唯一的,但這些表徵直線段在同一平面片中的絕對位置卻可以是任意的。
其中,常用的三維幾何變換包括平移變換、旋轉變換、比例變換、切錯變換等。這裡只列出了採用旋轉變換的方法。如圖3(a)、3(b)、3(c)所示,分別為繞Z軸在XOY平面內旋轉、繞X軸在YOZ平面內旋轉、繞Y軸在ZOX平面內旋轉的示意圖。
(i)繞Z軸旋轉的情況:
當繞Z軸旋轉時,即從Z軸正向軸往原點望去,在XOY平面內逆時針旋轉一定角度。針對角度的大小,逆時針方向旋轉角度數為正值,順時針方向旋轉角度為負值,如圖3(a)所示(從X正向軸旋轉+90度至Y正向軸)。具體計算公式如(1)所示。舉例而言,從任意位置開始旋轉+90度後坐標變換如公式(2)所示,如可以從(4,3,0,1)旋轉至(-3,4,0,1)。
(ii)繞X軸旋轉的情況:
當繞X軸旋轉時,即從X正向軸往原點望去,在YOZ平面內逆時針旋轉一定角度。針對角度的大小,逆時針方向旋轉角度為正值,順時針旋轉角度為負值,如圖3(b)所示(從Y正向軸旋轉+90度至Z正向軸)。具體計算公式如(3)所示。舉例而言,從任意位置開始旋轉+90度後坐標變換為公式(4)所示,如可以從(0,4,3,1)旋轉至(0,-3,4,1)。
(iii)繞Y軸旋轉的情況:
當繞Y軸旋轉時,即從Y軸正向軸往原點望去,在ZOX平面內逆時針旋轉一定角度。針對角度的大小,逆時針方向旋轉角度為正值,順時針旋轉角度為負值,如圖3(c)所示(從Z正向軸旋轉+90度至X正向軸)。具體計算公式如(5)所示。舉例而言,從任意位置開始旋轉+90度後坐標變換為公式(6)所示,如可以從(4,0,3,1)旋轉至(3,0,-4,1)。
以上給出了幾何變化中旋轉操作的變換矩陣(分別是繞Z軸旋轉、繞X軸旋轉、繞Y軸旋轉),變換矩陣分別是Matrix(1),Matrix(2),Matrix(3)。
針對旋轉操作,採用如下計算兩個二維向量(x1,y1)與(x2,y2)所形成方向角(directionAngle),這在後面會多處被調用:
cosValue=(x1*x2+y1*y2)/(Math.sqrt(x1*x1+y1*y1)*Math.sqrt(x2*x2+y2*y2))
(7)
betweenAngle=Math.arccos(cosValue)(8)
x1<0,directionAngle=2*PI-betweenAngle (9)
x1≥0,directionAngle=betweenAngle (10)
其中,Math.sqrt表示求取平方根的函數,PI為圓周率。
可選地,所述步驟S23具體包括:
B1、計算起始法向量(initFN.x,initFN.y)與(0,1)形成的方向角angle1,所述起始法向量為所述預設的起始平面的法向量。具體地,利用上面的公式(7)至(10)計算(initFN.x,initFN.y)與(0,1)形成的方向角angle1。其中,initFN.x為起始法向量initFN在X軸上的分量,同理,initFN.y為起始法向量initFN在Y軸上的分量。
B2、根據所述angle1將環繞直線段所形成的矢量rSegV從三維空間變換為位於YOZ平面上的rSegV_YOZ。具體地,通過下式將環繞直線段所形成的矢量rSegV從三維空間變換為位於YOZ平面上的rSegV_YOZ:
{rSegV_YOZ.x,rSegV_YOZ.y,rSegV_YOZ.z,1}={rSegV.x,rSegV.y,rSegV.z,1}Matrix(1)(angle1) (11)
B3、計算所述rSegV_YOZ與(0,1)形成的方向角angle2。其中,angle2的計算與angle1的類似,此處不再贅述。
B4、根據所述angle2將所述rSegV_YOZ變換為Z軸正向,以將對應的二維平面投影至XOY平面。具體地,通過下式將對應的二維平面投影至XOY平面:
{rSegV_Z.x,rSegV_Z.y,rSegV_Z.z,1}={rSegV_YOZ.x,rSegV_YOZ.y,rSegV_YOZ.z,1}Matrix(2)(angle2) (13)
步驟S24,將預設的起始平面變換為X軸正向,且所述起始平面的法向量變換為X軸正向朝上,所述預設的起始平面為所述三維實體包含的二維平面中的任一個二維平面,所述預設的起始平面的表徵矢量為起始表徵矢量。
假設起始法向量標記為initFN,則起始表徵矢量的各個分量計算公式如下:
iResSegV.x=initFN.y*rSegV.z-initFN.z*rSegV.y (15)
iResSegV.y=initFN.z*rSegV.x-initFN.x*rSegV.z (16)
iResSegV.z=initFN.x*rSegV.y-initFN.y*rSegV.x (17)
可選地,所述步驟S24具體包括:
C1、根據所述angle1和所述angle2將所述起始表徵矢量iResSegV轉換為XOY平面的矢量iResSegV_XOY。
C2、計算(-iResSegV_XOY.y,iResSegV_XOY.x)與(0,1)形成的方向角angle3。
C3、根據所述angle3將所述iResSegV_XOY變換為X軸正向的iResSegV_X,以將預設的起始平面變換為X軸正向,且所述起始平面的法向量變換為X軸正向朝上。
上述C1~C3中,對於起始表徵矢量(iResSegV)進行兩次旋轉,即根據angle1實現第一次旋轉,根據angle2實現第二次旋轉。具體公式如下:
iResSegV_XOY=iResSegV*Matrix(1)(angle1)*Matrix(2)(angle2) (18)
再計算(-iResSegV_XOY.y,iResSegV_XOY.x)與(0,1)形成的方向角angle3,其中,angle3的計算與angle1的類似,此處不再贅述。
之後,根據angle3實現第三次旋轉(仍然使用變換矩陣Matrix(1)),此時不僅環繞直線段(rSeg)所形成的矢量為Z軸正向,同時X軸正向與X軸正向朝上也分別代表起始平面片和起始平面片方向,具體如下:
{iResSegV_X.x,iResSegV_X.y,iResSegV_X.z,1}=
{iResSegV_XOY.x,iResSegV_XOY.y,iResSegV_XOY.z,1}Matrix(1)(angle3)(19)
通過上述計算得到三個旋轉方位角(即angle1,angle2,angle3)和對應旋轉矩陣(即Matrix(1),Matrix(2),Matrix(1)),將它們作用於每個平面從而得到對應的表徵矢量,運算後的所有表徵矢量統一位於XOY平面,便於下一步比較。
步驟S25,在XOY平面上,計算起始表徵矢量與確定的其他表徵矢量的夾角,並根據夾角的大小確定對應的二維平面與預設的起始平面的遠近。
可選地,所述步驟S25具體包括:
D1、在XOY平面上,分別判斷所述iResSegV_X的分量iResSegV_X.x、iResSegV_X.y與0的大小關係。
D2、根據判斷結果選擇計算起始表徵矢量與確定的其他表徵矢量的夾角的方式,並根據夾角的大小確定對應的二維平面與預設的起始平面的遠近。
將平面統一到XOY平面後,沿著Z軸正方向往原點望去,基於共享直線段的平面束已經簡化為了基於共享點的直線段束。故而,能夠計算從X軸正向(即起始表徵矢量,代表起始平面)出發,與每個表徵矢量(代表每個平面)所形成的角度大小(總是沿著逆時針)。
此時,顧及所處空間象限而計算角度,方法如下:
iResSegV_X.x≥0並且iResSegV_X.y≥0,那麼
_angle=Math::arccos(iResSegV_X.x) (21)
iResSegV_X.x≤0並且iResSegV_X.y≥0,那麼
_angle=PI-Math::arccos(-iResSegV_X.x)(22)
iResSegV_X.x≤0並且iResSegV_X.y≤0,那麼
_angle=PI+Math::arccos(-iResSegV_X.x)(23)
iResSegV_X.x≥0並且iResSegV_X.y≤0,那麼
_angle=2*PI-Math::arccos(iResSegV_X.x) (24)
比較這些角度,找出最大角和最小角。其中,最小角表示其所在的表徵矢量對應的平面即「從起始平面片出發,沿著其法向量所指方向的最鄰近平面」,簡稱「最近平面」;最大角表示其所在的表徵矢量對應的平面即「從起始平面出發,沿著其法向量所指方向的最遠平面」,簡稱「最遠平面」。
本發明第一實施例中,確定三維實體包含的二維平面,確定所述二維平面的表徵矢量,根據所述二維平面的表徵矢量將對應的二維平面投影至XOY平面,將預設的起始平面變換為X軸正向,且所述起始平面的法向量變換為X軸正向朝上,所述預設的起始平面為所述三維實體包含的二維平面中的任一個二維平面,所述預設的起始平面的表徵矢量為起始表徵矢量,在XOY平面上,計算起始表徵矢量與確定的其他表徵矢量的夾角,並根據夾角的大小確定對應的二維平面與預設的起始平面的遠近。由於將三維實體包含的二維平面都投影至XOY平面,因此,在XOY平面上,計算的起始表徵矢量與確定的其他表徵矢量的夾角的大小即表示該其他表徵矢量對應的二維平面與預設的起始平面的遠近,從而能夠確定三維實體包含的各個二維平面的遠近關係,進而實現三維實體的構造。
參考圖4,為了更清楚直觀地闡述幾個重要概念的(典型的如共享直線段、環繞方向、表徵矢量等),下面以具體的示例進行說明:
圖5(a)、圖5(b)、圖5(c)(下面為了方便描述,用圖5表示圖5(a)、圖5(b)、圖5(c)中的任一個)給出了在三維空間中幾何變換過程,圖6(a)、圖6(b)(下面為了方便描述,用圖6表示圖6(a)、圖6(b)中的任一個)放大了平面束從而給出了平面片中每個平面片中直線段的走向。具體的,由附圖5可見,AB是共享直線段(其本身具有物理方向,該物理方向是固定的、唯一的);同時,由圖6可見,AB在每個平面片中有著不同的環繞方向,包括:
(i)AB在平面片f2中的環繞方向為由B指向A(故而平面片f2一般表述為BAPO,其法向量指向右側)。
(ii)AB在平面片f1中的環繞方向為由B指向A(故而平面片f1一般表述為BADC,其法向量指向右側)。
(iii)AB在平面片f5中的環繞方向為由A指向B(故而平面片f5一般表述為ABEF,其法向量指向左側)。
如附圖5所示,一共存在5個平面片,也即存在5個表徵矢量,包括:
(i)平面片f2的表徵矢量為AP(由「平面片f2的法向量(指向右側)」與「AB在平面片f2中的環繞方向(如上所述,即由B指向A)」通過右手定則叉乘獲得)。
(ii)平面片f1的表徵矢量為AD(由「平面片f1的法向量(指向右側)」與「AB在平面片f1中的環繞方向(如上所述,即由B指向A)」通過右手定則叉乘獲得)。
(iii)平面片f5的表徵矢量為AF(由「平面片f5的法向量(指向左側)」與「AB在平面片f5中的環繞方向(如上所述,即由A指向B)」通過右手定則叉乘獲得)。
值得注意的是,針對表徵矢量的獲得(平面片f2的表徵矢量是AP、平面片f1的表徵矢量是AD、平面片f5的表徵矢量是AF),雖然通過圖形直觀分析是顯而易見的(即由圖5(a)和圖5(b)很容易在圖5(c)中看出以上表徵矢量,即共享直線段AB中A點仍然可見而B點被遮住,平面片f2異於AB的一側中O點被P點遮住而造成平面片f2簡化表徵為AP,平面片f1異於AB的一側中C點被D點遮住而造成平面片f1簡化表徵為AD,平面片f5異於AB的一側中E點被F遮住從而平面片f5被簡化表徵為AF),但是要在計算機中實現以上平面片對應表徵矢量的準確獲得卻並不能依靠可視化讀圖,故而以上共享直線段、環繞方向、平面片法向量的計算以及右手叉乘運算都是必須的。
通過以上計算步驟,可以發現:無論每個平面片的法向量如何變化(有的指向左側,而有的指向右側)、無論共享直線段在每個平面片的環繞方向如何變化(有的從直線段的物理起點指向物理終點,而有的從直線段的物理終點指向物理起點),基於共享直線段的平面束的表徵矢量集合始終是呈現「從中心往周邊的(類似花束的)散髮狀」的。換言之,每個嵌入於三維空間中的二維平面束排序都可以簡化為嵌入於二維空間中的一維直線段束排序。特別的,以平面片f1的表徵矢量AD出發(即起始表徵矢量),找到的最近表徵矢量為AF(代表平面片f5),找到的最遠表徵矢量為AP(代表平面片f2)。
作為進一步補充,這裡再給出一個簡單案例來直觀闡述平面束排序,其圖形與對應統計數據分別如附圖7(a)-(c)和表1所示。
具體的,在三維空間中,共享直線段的起點和終點分別是sPt和ePt(如圖7(a)所示),其本身「物理方向」(-0.460,0.624,-0.632)。相接於該共享直線段的平面片集合包括Facet_A,Facet_B,Facet_C,Facet_D,Facet_E,Facet_F,Facet_G(如圖7(b)所示)。根據該共享直線段本身「物理方向」與其在平面片中「環繞方向」的異同,以上平面片集合可以分為兩組,一組是Facet_E,Facet_D,另一組是Facet_G,Facet_C,Facet_A,Facet_F,Facet_B。針對上述每個平面片,首先如上計算其表徵矢量,之後如上計算三個旋轉方位角(及相應旋轉矩陣)並實現每個平面片表徵矢量的幾何表換,具體如表1中後面幾列所示。
表1:
其中,在幾何變換後(如圖7(c)所示),共享直線段簡化為O點;由於Facet_B是起始平面片,故而表徵矢量ob(代表Facet_B)被簡化為X軸正向:從ob出發,沿著逆時針方向望去,依次排列的分別是oa(代表Facet_A),og(代表Facet_G),of(代表Facet_F),oe(代表Facet_E),od(代表Facet_D),oc(代表Facet_C)。其中,oa與ob形成角度最小,代表Facet_A是Facet_B的「最近平面片」;oc與ob形成的角度最大,代表Facet_C是Facet_B的「最遠平面片」,這與實際情況統計的比較結果是一致的。
在這裡,為了能夠更詳細地闡述本發明提出的基於共享直線段的平面片束排序方法,將其應用於「基於統一邏輯的構體方法」與「基於左轉(或方位角)的構體方法」(在技術背景中已經給出)。其基本原理與具體實現(包括本發明給出的三大步驟)都一樣;以上兩種構體方法的區別在於,前者會一邊尋體一邊詳細記錄構體過程中每個平面片如何使用(每個平面片最多被使用2次)從而準確定位目標體集合(最多找到一個包含所有最小體的最大體,該最大體是不需要的);而後者尋體是盲目的搜索,會發現除了目標體(也稱有效體)之外的許多錯誤體和冗餘體,需要事後(通過體積計算等)剔除。
同時,採用典型三維案例用於驗證,這些案例來自中國廣東省深圳市的三維產權體數據(三維宗地及三維建築體),包括:
(1)後海地下停車場(Underground Parking Lot,簡寫為UPL);
(2)卓越世紀中心(Excellence Century Center,簡寫為ECC);
(3)深港西部通道(Hongkong-Shenzhen Western Corridor,簡寫為HSWC);
(4)中興通訊(Zhongxin Telecommunication Center,簡寫為ZTC);
(5)供電局(Power Supply Building,簡寫為PSB);
(6)華潤萬象成(MixC);
(7)會展中心(Convention&Exhibition Center);
(8)瀚盛花園小區B1建築體1-7層;
(9)瀚盛花園小區B2建築體1-8層;
(10)瀚盛花園小區B3建築體1-5層;
(11)瀚盛花園小區B4建築體1-8層;
以上三維案例的對應統計數據如表2所示。
表2:
如表2所示,在每個案例中,代表初始平面片的個數,描述了輸入數據;在基於ACSEBUL方法給予尋體的過程中,涉及參數包括外部平面片個數(exterior Facet,簡寫為eF)、內部平面片個數(interior Facet,簡寫為iF)、排序找結束平面片次數(sort last Facet,簡寫為slF)、排序找起始平面片次數(sort first Facet,簡寫為sfF)、排序找平面片總次數(sort Facet,簡寫為sF)、分配給每個平面片的平均排序次數(sort Per Facet,簡寫為sPF)、尋到體個數(Body,簡寫為B);在基於左轉(右轉)方法、方位角方法給予尋體的過程中,涉及參數包括排序找平面片次數(sort Facet 1,簡寫為sF1)、分配給每個平面片的平均排序次數(sort Per Facet1,簡寫為sPF1)、尋到所有體個數(all Body,簡寫為aB)、分配給每個平面片的平均搜索體個數(all body Per Facet,簡寫為abPF)、找到的錯誤體個體(error Body,簡寫為eB)、找到的冗餘體個數(duplicated Body,簡寫為dB)、找到的有效體個數(valid Body,簡寫為vB)、尋體有效率(Valid Ratio,簡寫為VR)。特別的,在這裡還將每個普通平面片(每個平面片包含至少3條邊)以構造邊為約束給予三角化剖分(Constrained Delaunay Triangulation,簡寫為CDT)後再次給予構體操作。換言之,此時用於構體的每個平面片就是三角形面片(三角形面片是普通平面片的特例)。
具體的,在前者尋體方法中,每個平面片包含至少3條邊,從每條邊出發能確定唯一的最鄰近平面片(由sfF代表),由每條邊出發能確定唯一的最遠平面片(由slF代表),sF代表構體過程中的排序總次數,sPF代表分攤至每個平面片的平均排序次數。它們滿足如下:
sF=slF+sfF=2*slF=2*sfF (25)
sPF=sF/F≥6 (26)
在平面片給予CDT情況中,每個平面片都是三角形(具有確定的三條邊),滿足如下:
sPF=sF/F=6(27)
相對的,在後者尋體方法中,由於是盲目尋找並事後剔除無效體(包括錯誤體和冗餘體),故而會大大增加平面片的排序次數;尤其是在給予面片CDT的情況下,構成同一個有效體的面片數大幅度增加,那麼會造成找到的錯誤體和冗餘體也更多。它們滿足如下:
aB=eB+dB+vB (28)
VR=vB/aB,VB(usingCDT)sF,sPF1>sPF (30)
以上三維案例成功驗證了基於共享直線段的平面束排序的數值計算過程(包括三個大步驟)的正確性。
應理解,在本發明實施例中,上述各過程的序號的大小並不意味著執行順序的先後,各過程的執行順序應以其功能和內在邏輯確定,而不應對本發明實施例的實施過程構成任何限定。
實施例二:
圖8示出了本發明第二實施例提供的一種基於共享直線段的平面片束排序系統的結構圖,該基於共享直線段的平面片束排序系統可用於移動終端中,該移動終端可以包括經無線接入網RAN與一個或多個核心網進行通信的用戶設備,該用戶設備可以是行動電話(或稱為「蜂窩」電話)、具有行動裝置的計算機等,例如,用戶設備還可以是可攜式、袖珍式、手持式、計算機內置的或者車載的移動裝置,它們與無線接入網交換語音和/或數據。又例如,該行動裝置可以包括智慧型手機、平板電腦、個人數字助理PDA、銷售終端POS或車載電腦等。為了便於說明,僅示出了與本發明實施例相關的部分。
該基於共享直線段的平面片束排序系統包括:二維平面確定單元81、表徵矢量確定單元82、平面投影單元83、起始平面變換單元84、表徵矢量的夾角計算單元85。其中:
二維平面確定單元81,用於確定三維實體包含的二維平面。
表徵矢量確定單元82,用於確定所述二維平面的表徵矢量。
可選地,所述表徵矢量確定單元82包括:
二維平面的法向量確定模塊,用於確定所述二維平面的法向量和環繞方向。
法向量和環繞方向叉乘模塊,用於叉乘所述二維平面的法向量和環繞方向,叉乘的結果為所述二維平面的表徵矢量。
平面投影單元83,用於根據所述二維平面的表徵矢量將對應的二維平面投影至XOY平面。
可選地,所述平面投影單元83包括:
第一方向角計算模塊,用於計算起始法向量(initFN.x,initFN.y)與(0,1)形成的方向角angle1,所述起始法向量為所述預設的起始平面的法向量,根據所述angle1將環繞直線段所形成的矢量rSegV從三維空間變換為位於YOZ平面上的rSegV_YOZ。具體地,利用上面的公式(7)至(10)計算(initFN.x,initFN.y)與(0,1)形成的方向角angle1。其中,initFN.x為起始法向量initFN在X軸上的分量,同理,initFN.y為起始法向量initFN在Y軸上的分量。
第二方向角計算模塊,用於計算所述rSegV_YOZ與(0,1)形成的方向角angle2,根據所述angle2將所述rSegV_YOZ變換為Z軸正向,以將對應的二維平面投影至XOY平面。
起始平面變換單元84,用於將預設的起始平面變換為X軸正向,且所述起始平面的法向量變換為X軸正向朝上,所述預設的起始平面為所述三維實體包含的二維平面中的任一個二維平面,所述預設的起始平面的表徵矢量為起始表徵矢量。
可選地,所述起始平面變換單元84包括:
起始表徵矢量轉換模塊,用於根據所述angle1和所述angle2將所述起始表徵矢量iResSegV轉換為XOY平面的矢量iResSegV_XOY。
第三方向角計算模塊,用於計算(-iResSegV_XOY.y,iResSegV_XOY.x)與(0,1)形成的方向角angle3。根據所述angle3將所述iResSegV_XOY變換為X軸正向的iResSegV_X,以將預設的起始平面變換為X軸正向,且所述起始平面的法向量變換為X軸正向朝上。
表徵矢量的夾角計算單元85,用於在XOY平面上,計算起始表徵矢量與確定的其他表徵矢量的夾角,並根據夾角的大小確定對應的二維平面與預設的起始平面的遠近。
可選地,所述表徵矢量的夾角計算單元85包括:
分量比較模塊,用於在XOY平面上,分別判斷所述iResSegV_X的分量iResSegV_X.x、iResSegV_X.y與0的大小關係。
夾角計算模塊,用於根據判斷結果選擇計算起始表徵矢量與確定的其他表徵矢量的夾角的方式,並根據夾角的大小確定對應的二維平面與預設的起始平面的遠近。
本發明第二實施例中,由於將三維實體包含的二維平面都投影至XOY平面,因此,在XOY平面上,計算的起始表徵矢量與確定的其他表徵矢量的夾角的大小即表示該其他表徵矢量對應的二維平面與預設的起始平面的遠近,從而能夠確定三維實體包含的各個二維平面的遠近關係,進而實現三維實體的構造。
本領域普通技術人員可以意識到,結合本文中所公開的實施例描述的各示例的單元及算法步驟,能夠以電子硬體、或者計算機軟體和電子硬體的結合來實現。這些功能究竟以硬體還是軟體方式來執行,取決於技術方案的特定應用和設計約束條件。專業技術人員可以對每個特定的應用來使用不同方法來實現所描述的功能,但是這種實現不應認為超出本發明的範圍。
所屬領域的技術人員可以清楚地了解到,為描述的方便和簡潔,上述描述的系統、裝置和單元的具體工作過程,可以參考前述方法實施例中的對應過程,在此不再贅述。
在本申請所提供的幾個實施例中,應該理解到,所揭露的系統、裝置和方法,可以通過其它的方式實現。例如,以上所描述的裝置實施例僅僅是示意性的,例如,所述單元的劃分,僅僅為一種邏輯功能劃分,實際實現時可以有另外的劃分方式,例如多個單元或組件可以結合或者可以集成到另一個系統,或一些特徵可以忽略,或不執行。另一點,所顯示或討論的相互之間的耦合或直接耦合或通信連接可以是通過一些接口,裝置或單元的間接耦合或通信連接,可以是電性,機械或其它的形式。
所述作為分離部件說明的單元可以是或者也可以不是物理上分開的,作為單元顯示的部件可以是或者也可以不是物理單元,即可以位於一個地方,或者也可以分布到多個網絡單元上。可以根據實際的需要選擇其中的部分或者全部單元來實現本實施例方案的目的。
另外,在本發明各個實施例中的各功能單元可以集成在一個處理單元中,也可以是各個單元單獨物理存在,也可以兩個或兩個以上單元集成在一個單元中。
所述功能如果以軟體功能單元的形式實現並作為獨立的產品銷售或使用時,可以存儲在一個計算機可讀取存儲介質中。基於這樣的理解,本發明的技術方案本質上或者說對現有技術做出貢獻的部分或者該技術方案的部分可以以軟體產品的形式體現出來,該計算機軟體產品存儲在一個存儲介質中,包括若干指令用以使得一臺計算機設備(可以是個人計算機,伺服器,或者網絡設備等)執行本發明各個實施例所述方法的全部或部分步驟。而前述的存儲介質包括:U盤、移動硬碟、只讀存儲器(ROM,Read-Only Memory)、隨機存取存儲器(RAM,Random Access Memory)、磁碟或者光碟等各種可以存儲程序代碼的介質。
以上所述,僅為本發明的具體實施方式,但本發明的保護範圍並不局限於此,任何熟悉本技術領域的技術人員在本發明揭露的技術範圍內,可輕易想到變化或替換,都應涵蓋在本發明的保護範圍之內。因此,本發明的保護範圍應所述以權利要求的保護範圍為準。
本專利受資助於「國土資源部城市土地資源監測與仿真重點實驗室開放基金資助課題(KF-2016-02-001).The Project Supported by the Open Fund of Key Laboratory of Urban Land Resources Monitoring and Simulation,Ministry of Land and Resources(KF-2016-02-001)」以及「測繪遙感信息工程國家重點實驗室資助項目及編號(15I03).Open Research Fund of State Key Laboratory of Information Engineering in Surveying,Mapping and Remote Sensing(15I03)」以及「國家自然科學基金資助項目(項目批准號:41601428).Project Supported by National Natural Science Foundation of China(Grant No.41601428)」以及「2016年度浙江省博士後科研項目擇優資助課題立項(立項課題名稱:關於LADM的我國不動產統一登記建模_以浙江省為例)」。
