一種多濾波器組及利用其進行濾波的方法與流程
2023-09-20 23:33:40 4
本發明涉及信號處理技術,尤其涉及利用小波分析理論進行信號處理的多濾波器組及利用該多濾波器組進行濾波的方法。
背景技術:
傳統的單小波不能同時擁有對稱、正交、緊支撐和高消失矩等性質。如大部分正交單濾波器是無限支集的,除了哈爾小波外,沒有任何緊支撐小波具有對稱性,但是哈爾小波僅有1階消失矩。
濾波器的對稱性在信號處理,尤其是圖像處理中是非常重要的,它通過有限長度信號的對稱擴張變換能有效地減少圖像的失真,如在圖像邊界延拓時可以通過對稱擴張來解決。而非對稱的正交單濾波器已形成較大誤差。在重構中,由係數產生的誤差將由濾波器擴展到整個信號內部,這種擴展的程度取決於濾波器支撐長度。支撐越長,誤差的擴展也就越明顯。消失矩表明了小波變換後信息頻域能量的集中程度,消失矩越高,小波變換後能量越集中於低頻部分,而在高頻部分會出現更多的零值。正則性是描述小波光滑性的重要指標。在對小波係數作量化或閾值的過程中,不可避免的要引入誤差。從圖像處理的角度來看,有相同能量大小的光滑誤差比非正則誤差在視覺上有更好的容忍度;所以多小波要求一定的正則性,以求獲得更好的重構圖像的質量。
另外,在信號分析和圖像處理中,小波的時頻特性非常重要。如在提取圖像和視頻信號的高頻成分如紋理、邊緣和運動信息時,要求濾波器在時域和頻域同時擁有好的能量集中能力。窗函數的頻域解析度越高越能分辨出頻譜中兩相鄰近的譜峰,時域解析度越高越能描述信號在時域內的變化。
多小波能同時擁有對稱、正交、緊支撐和高消失矩等性質,因此多小波及其多濾波器組具有廣闊的應用前景。儘管多小波理論研究取得了不少實質性的結果, 但將它們成功應用於信號與圖像處理中仍受到很大限制。目前,已有應用多小波的最優時頻解析度多濾波器組是非平衡的。在具體應用中,需要將這種非平衡的最優時頻解析度多濾波器組旋轉π/4角得到平衡多濾波器組。然而,通過這種平衡化方法得到的平衡多濾波器組不僅失去了對稱性,還改變了多濾波器組的時頻解析度,使得平衡後的多濾波器組的時頻解析度不再最優。
技術實現要素:
本發明旨在解決上面描述的問題。本發明的一個目的是提供一種多濾波器組及利用其進行濾波的方法。該多濾波器組能同時擁有對稱、正交、緊支撐和高消失矩等性質,還有更優的時頻解析度,且同時具有平衡性和對稱性。
根據本發明的第一方面,提供了一種多濾波器組,所述多濾波器組包括矩陣低通濾波器P(ω)和矩陣高通濾波器Q(ω),並且,其中,
其中,所述矩陣低通濾波器對應於兩個尺度函數φ1和φ2,其中φ(x)=(φ1,φ2)T,並且,所述矩陣高通濾波器對應於 兩個小波函數ψ1和ψ2,其中Ψ(x)=(ψ1,ψ2)T,
其中,所述兩個尺度函數和所述兩個小波函數的時窗半徑分別為和其中,
其中,f表示φj或ψj。
其中,所述兩個尺度函數和所述兩個小波函數的頻窗半徑分別為和其中,
其中,所述兩個尺度函數和所述兩個小波函數的時頻窗面積為S,其中,
根據本發明的第二方面,提供了一種利用多濾波器組進行濾波的方法,所述方法包括以下步驟:
構造所述多濾波器組,所述多濾波器組包括矩陣低通濾波器P(ω)和矩陣高通濾波器Q(ω),並且,其中,
將待濾波信號通過所述多濾波器組得到濾波信號。
其中,構造所述多濾波器組的步驟還包括:
設置所述矩陣低通濾波器對應於兩個尺度函數φ1和φ2,其中Φ(x)=(φ1,φ2)T, 並且,設置所述矩陣高通濾波器對應於兩個小波函數ψ1和ψ2,其中Ψ(x)=(ψ1,ψ2)T,
其中,構造所述多濾波器組的步驟還包括:
設置所述兩個尺度函數和所述兩個小波函數的時窗半徑分別為和其中,
其中,f表示φj或ψj。
其中,構造所述多濾波器組的步驟還包括:
設置所述兩個尺度函數和所述兩個小波函數的頻窗半徑分別為和其中,
其中,構造所述多濾波器組的步驟還包括:
設置所述兩個尺度函數和所述兩個小波函數的時頻窗面積為S,其中,
本發明的多濾波器組及其濾波方法同時具有平衡性和對稱性,和較佳的時頻 分辨性能。並且,還具有正交性、緊支撐性、高消失矩。
參照附圖來閱讀對於示例性實施例的以下描述,本發明的其他特性特徵和優點將變得清晰。
附圖說明
併入到說明書中並且構成說明書的一部分的附圖示出了本發明的實施例,並且與描述一起用於解釋本發明的原理。在這些附圖中,類似的附圖標記用於表示類似的要素。下面描述中的附圖是本發明的一些實施例,而不是全部實施例。對於本領域普通技術人員來講,在不付出創造性勞動的前提下,可以根據這些附圖獲得其他的附圖。
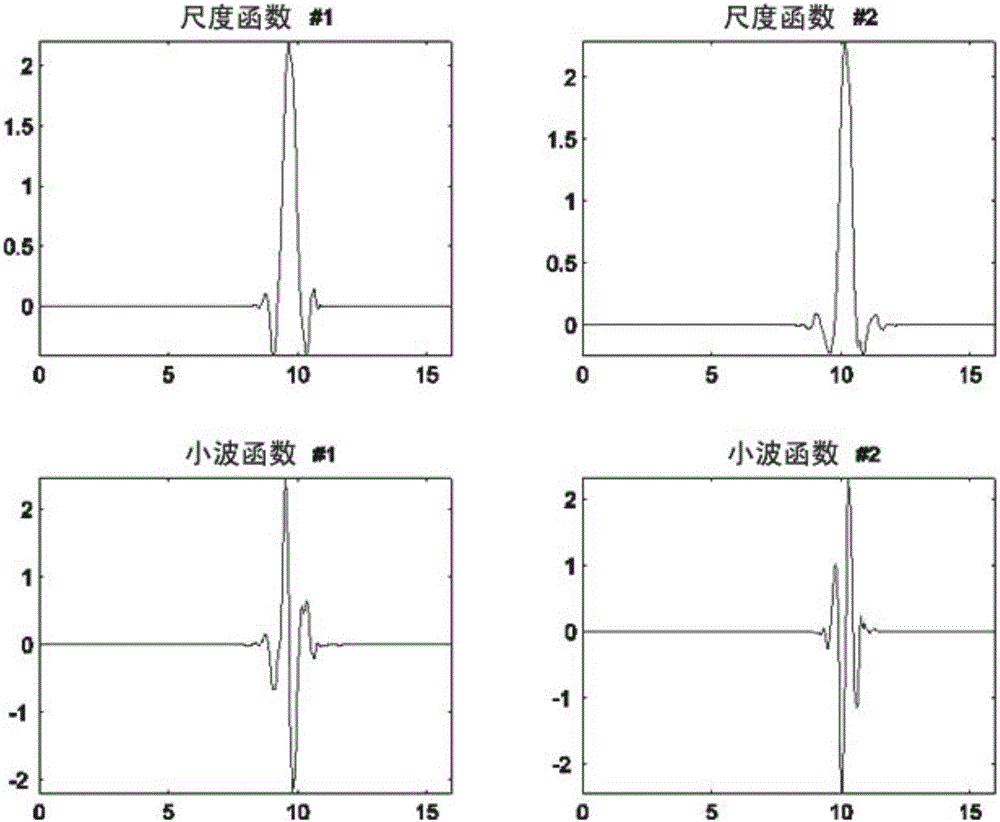
圖1示例性地示出了根據本發明的濾波器組的兩個尺度函數和兩個小波函數,即多濾波器組對應的尺度函數和小波函數;
圖2示例性地示出了根據本發明的濾波器組進行去噪實驗所用的圖像;
圖3示例性地示出了圖2中所用圖像Bridge的局部圖和去噪效果圖,即Bridge局部圖像的原圖及去噪效果圖。
具體實施方式
為使本發明實施例的目的、技術方案和優點更加清楚,下面將結合本發明實施例中的附圖,對本發明實施例中的技術方案進行清楚、完整地描述,顯然,所描述的實施例是本發明一部分實施例,而不是全部的實施例。基於本發明中的實施例,本領域普通技術人員在沒有做出創造性勞動前提下所獲得的所有其他實施例,都屬於本發明保護的範圍。需要說明的是,在不衝突的情況下,本申請中的實施例及實施例中的特徵可以相互任意組合。
本發明的基本思想是,設計一種多濾波器組,其在具有出色的時頻分辨性能前提下,還具有平衡性和對稱性。
本發明提供了一種多濾波器組,該多濾波器組包括矩陣低通濾波器P(ω)和矩陣高通濾波器Q(ω),並且,其中Pk和Qk具體如下:
分別是{Pk}和{Qk}的矩陣頻率響應,P(ω)即為矩陣低通濾波器,Q(ω)即為矩陣高通濾波器。Pk和Qk則為矩陣濾波器係數。後面為了表述方便,用{P,Q}表示本發明的多濾波器組。
上述的矩陣低通濾波器對應於兩個尺度函數φ1和φ2,其中Φ(x)=(φ1,φ2)T, 上述的矩陣高通濾波器對應於兩個小波函數ψ1和ψ2,其中Ψ(x)=(ψ1,ψ2)T,
分析上述給出的矩陣濾波器係數Pk和Qk可以看出,低通濾波器是對稱的,高通濾波器是鏡像對稱的。這種對稱性也可由對應於高通濾波器的兩個小波函數和對應於低通濾波器的兩個尺度函數看出。
圖1示出了根據本發明的對應於高通濾波器的兩個小波函數和對應於低通濾波器的兩個尺度函數。其中尺度函數小波函數 在頻域上,由圖1可知,兩個尺度函數Φ是近似對稱的,兩個小波函數Ψ是近似鏡像對稱的。
在實際濾波應用中,多濾波器組的對稱性表現在通過有限長度信號的對稱擴 張變換能有效地減少信號的失真。
另外,上述兩個尺度函數和兩個小波函數的時窗半徑分別是和其中,
其中,f表示φj或ψj。即,
上述兩個尺度函數和兩個小波函數的頻窗半徑分別是和其中,
在信號分析和圖像處理中,小波的時頻特性非常重要。衡量時頻解析度的重要指標是時窗半徑Δf和頻窗半徑Δf。Δf和Δf有時也稱持續時間和有效帶寬。稱窗函數f的時窗半徑與頻窗半徑之乘積ΔfΔf為解析度單元。在實際應用中希望窗函數的時域和頻域分辨能力同時提高時,要求窗函數的時窗半徑Δf和頻窗半徑Δf都要小。但是由海森堡測不準原則可知,ΔfΔf≥1/2。因此時域、頻域的解析度不可能無限制的同時提高。為了使本發明的多濾波器組的時頻解析度高儘可能地高,在海森堡測不準原則允許範圍之內,儘可能地同時提高窗函數在時域、頻域中的分辨能力,即使乘積ΔfΔf最小。
若φ=(φ1,…,φr)T和Ψ=(ψ1,…,ψr)T的每一個分量φj、ψj都是規範的,可以得到尺度函數和小波函數的每一個分量的頻窗半徑
此外,各尺度函數和小波函數的分辨單元之和為時頻窗面積S,其中 該時頻窗面積S就是衡量時頻解析度好壞的指標,S越小,時頻解析度越好。經過計算,本發明的多濾波器組的時頻窗面積為6.4712,遠小於其他的多濾波器組。
本發明還提供了一種利用多濾波器組進行濾波的方法。該方法包括:構造多濾波器組;將待濾波信號通過所述多濾波器組得到濾波信號。
在構造多濾波器組的步驟中,構造該多濾波器組包括矩陣低通濾波器P(ω)和矩陣高通濾波器Q(ω),並且,其中,P0,P0,...,P9以及Q0,Q0,...,Q9的取值如上所述,因此不再贅述。
構造多濾波器組的步驟還包括:設置矩陣低通濾波器對應於兩個尺度函數φ1和φ2,其中Φ(x)=(φ1,φ2)T,並且,設置矩陣高通濾波器對應於兩個小波函數ψ1和ψ2,其中Ψ(x)=(ψ1,ψ2)T,
構造多濾波器組的步驟還包括:設置兩個尺度函數和兩個小波函數的時窗半徑分別為和其中,
其中,f表示φj或ψj。
構造多濾波器組的步驟還包括:設置兩個尺度函數和兩個小波函數的頻窗半徑分別為和其中,
構造所述多濾波器組的步驟還包括:設置兩個尺度函數和兩個小波函數的時 頻窗面積為S,其中,
由前述可知,本發明的多濾波器組具有較好的對稱性,和較佳的時頻分辨性能。下面說明本發明的多濾波器還具有正交性、緊支撐性、高消失矩,和平衡性。
多濾波器組{P,Q}滿足
P(ω)P*(ω)+P(ω+π)P*(ω+π)=I2,ω∈[-π,π]
,Q(ω)Q*(ω)+Q(ω+π)Q*(ω+π)=I2,ω∈[-π,π]
P(ω)Q*(ω)+P(ω+π)Q*(ω+π)=02,ω∈[-π,π]
其中,M*表示M的Hermitian伴隨矩陣,I2表示2×2單位矩陣。由上述方程組可知,多濾波器組{P,Q}為矩陣共軛正交濾波器(MCQF)。
H9是支集在[-9,9]內的實係數三角多項式的2×2矩陣集合。在H9內定義變換算子TP,
定義變換算子TP的表達矩陣TP
TP=(2A2i-j)-8≤i,j≤8,其中
多濾波器組{P,Q}是MCQF,且變換算子TP滿足E條件,因此,Φ和Ψ是穩定的正交多尺度函數和多小波函數。
經過計算存在1×2實的行向量使得下式成立,
由計算可知,Φ具有2階逼近階。又因為Φ是穩定的,所以Φ具有2階逼近階等價於P滿足2階消失矩條件。
此外,若則Φ在Sobolev空間Ws(R)內。經過計算,估計本發明的多濾波器組的Sobolev正則指數為1.9963。由於緊支正交 小波函數可由尺度函數有限組合而成,所以小波函數具有和尺度函數相同的正則指數。
多濾波器組{P,Q}的低通變換算子LT能保留信號u0=(…,1,1,1,1,…)T,即LTu0=u0,所以正交多尺度函數Φ是平衡的。其中,
下面通過對比的方式,說明本發明的多濾波器組的優秀性能。表1給出了本發明的多濾波器組及其他多濾波器組的性質比較。其中,GHM與{P,Q}有相同的支撐特性,但支撐長度遠短於{P,Q};J_EX2、J_EX4分別是非平衡最優時頻解析度多濾波器組;{Ps,Qs}是與{P,Q}有相同的支撐長度,且具有最高Sobolev[8]正則指數的多濾波器組。
表1本發明多濾波器組與其他多濾波器組性質比較
(1)與J_EX2、J_EX4相比,本發明的多濾波器組的時頻解析度更優,並且具有平衡性。
本發明的多濾波器組的時頻窗面積僅有6.4761,不僅時頻解析度遠遠優於J_EX2、J_EX4,而且同時是平衡的且具有對稱性。在實際應用中,J_EX2、J_EX4等非平衡多濾波器組需旋轉π/4角得到平衡多濾波器組。通過這種平衡化方法得到的平衡多濾波器組不僅失去了對稱性,還改變了多濾波器組的時頻解析度,使得平衡後的多濾波器組的時頻解析度不再最優。
(2)與經典的GHM多小波函數相比,雖然本發明的多濾波器組對應的多 小波函數和GHM有相同的支撐特性,即ψ1與ψ2的濾波器長度相差4,但是在支撐長度遠大於GHM的情況下,時頻解析度遠優於GHM。
(3)本發明的多濾波器組{P,Q}的時頻解析度遠優於具有最高Sobolev正則指數的{Ps,Qs},並且,時頻窗面積小了5.7之多。
因此,由表1可以看出,本發明的多濾波器組相較於其他濾波器組而言,具有優秀的時頻性、平衡性、支撐長度等性質。
下面針對本發明的多濾波器組給出具體的濾波效果測試實驗。
為了體現本發明的多濾波器組的性能,本文採用如圖2所示的六張512×512灰度圖像進行去噪實驗。其中(a)表示平滑圖像Lena,(b)、(d)、(e)分別表示紋理豐富的圖像Barbara、Bridge、Clown,(c)、(f)分別表示圖像Lake和Man。在具體的去噪過程中,首先生成了三種不同的噪聲強度(噪聲方差分別為10、20和30)的含噪圖像,然後對每種含噪圖像進行5級分解,並用Levent提出的Bivariate閾值方案去噪,最後通過小波逆變換重構出去噪圖像。
比較實驗選用了文獻中的多種多濾波器組,包括在圖像處理領域具有非常優越性能的SA4多濾波器組。
表2、表3和表4分別給出了不同多濾波器組含噪和去噪後重構圖像的峰值信噪比PSNR值。其中,粗體的數字為PSNR值最好的實驗數據。由表2、表3和表4的實驗數據可以看出,本發明的多濾波器組{P,Q}的PSNR值是較佳的。
表2圖像Lena和Barbara在不同噪聲方差下的PSNR值
表3圖像Lake和Bridge在不同噪聲方差下的PSNR值
表4圖像Clown和Man在不同噪聲方差下的PSNR值
具體地,圖3示出了Bridge的局部圖和去噪效果圖,其中圖3中的(d1)、(d2)、(d3)和(d4)分別是Bridge局部圖像的原圖、σ=10的加噪圖、SA4去噪效果圖和{P,Q}去噪效果圖。由圖3可以看出,利用本發明的多濾波器組{P,Q}進行去噪的效果最好。
對圖2中示出的六張圖片進行去噪處理後的實驗數據顯示,本發明的多濾波器組{P,Q}由於同時具有時頻解析度高、平衡性和對稱性等性質,因此其去噪效果:(1)明顯優於在圖像處理領域具有非常優越性能的SA4;(2)明顯優於非平衡的,但是時頻解析度好的J_EX2、J_EX4;(3)明顯優於平衡的、最優正則性和消失矩高,但是時頻解析度差的Ψs。
由此可以看出,本發明的具有時頻解析度高、平衡性和對稱行等性質的正交緊支多濾波器組不僅在理論上具有優良性質,在實際應用中也能顯示優秀的性能。
上面描述的內容可以單獨地或者以各種方式組合起來實施,而這些變型方式都在本發明的保護範圍之內。
最後應說明的是:以上實施例僅用以說明本發明的技術方案,而非對其限制。儘管參照前述實施例對本發明進行了詳細的說明,本領域的普通技術人員應當理解:其依然可以對前述各實施例所記載的技術方案進行修改,或者對其中部分技術特徵進行等同替換;而這些修改或者替換,並不使相應技術方案的本質脫離本發明各實施例技術方案的精神和範圍。
