二元擴域上SM2加密算法的實現方法與流程
2023-09-18 14:48:30 6
本發明具體涉及二元擴域f2m上sm2橢圓曲線公鑰密碼算法的公鑰加密算法實現。
背景技術:
橢圓曲線密碼算法的快速實現一直是橢圓曲線密碼體制研究的重點,基於有限域上的橢圓曲線可以實現數據加密等密碼方案。
二元擴域上橢圓曲線可以用仿射坐標、標準射影坐標、jacobian加重射影坐標以及lopez&dahab射影坐標表示,根據橢圓曲線特點和坐標的具體形式對點加和倍點運算進行優化,通過對幾種情況下的優化,由圖1得到lopez&dahab射影坐標下的點加和倍點運算的運算速度最快。
多倍點運算是橢圓曲線密碼算法的核心運算。對於多倍點運算的實現方式有很多種,其中,基於k的有符號二進位展開的滑動窗口算法的實現速度最快。
橢圓曲線公鑰加密算法中涉及到的雜湊函數使用sm3模塊來實現,這個模塊主要包括頂層模塊、controller控制器、消息擴展模塊、消息壓縮模塊以及結果讀取。降低了電路開銷,總體上提升了整個算法流程的速度。
技術實現要素:
本發明所要解決的技術問題是:針對上述存在的問題,提供了一種二元擴域f2m上sm2橢圓曲線公鑰密碼算法的公鑰加密算法實現方法,通過提高點乘和雜湊函數等的計算速度來有效的提升sm2公鑰加密算法的性能。
為解決上述技術問題,本發明的sm2公鑰加密算法的實現方法,包括如下步驟:
步驟一:用隨機數發生器產生隨機數k∈[1,n-1];
步驟二:計算橢圓曲線點c1=[k]g=(x1,y1),將c1的數據類型轉換為比特串,其中g為橢圓曲線的一個基點;
步驟三:計算橢圓曲線點s=[h]pb,若s是無窮遠點,則報錯並退出,其中pb為用戶b的公鑰;
步驟四:計算橢圓曲線點s1=[k]pb=(x2,y2),將坐標x2、y2的數據類型轉換為比特串;
步驟五:計算t=kdf(x2∥y2,klen),若t為全0比特串,則返回步驟一,其中kdf(z,klen)為密鑰派生函數,x∥為x與y的拼接;
步驟六:計c2=m⊕t,其中⊕為長度相等的兩個比特串按比特的異或運算;
步驟七:計算c3=hash(x2∥m∥y2),其中hash為密碼雜湊函數;
步驟八:輸出密文c=c1∥c2∥c3。
本發明在二元擴域上使用ld投影坐標運算,對於點乘運算採用快速的基於k的有符號的二進位展開的滑動窗口算法以及使用集成的sm3模塊計算雜湊值,可以提升sm2公鑰加密算法的性能。
附圖說明
下面結合附圖與具體實施方式對本發明作進一步詳細的說明:
圖1是所述sm2公鑰加密算法的實現方法的流程圖;
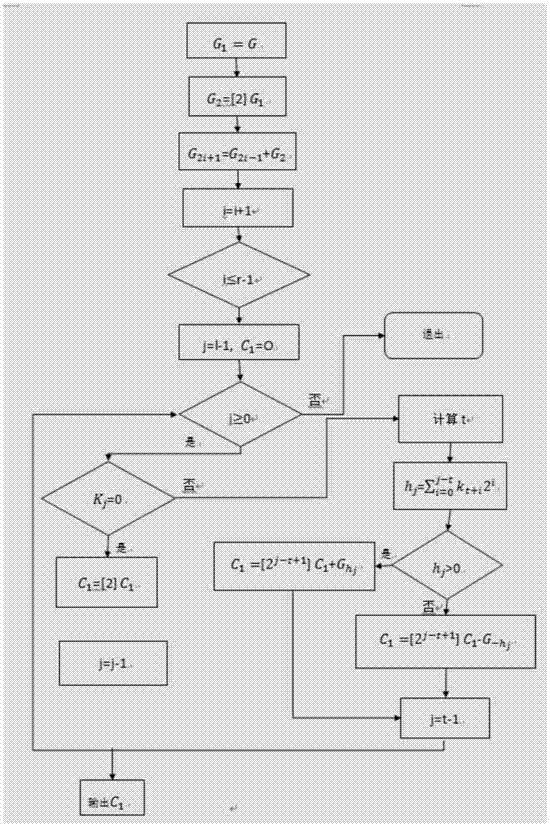
圖2是計算c1=[k]g=(x1,y1)的流程圖。
圖3是sm3模塊的埠設計圖。
具體實施方式
二元擴域f2m上sm2橢圓曲線公鑰密碼算法的公鑰加密算法實現方法如圖1所示。
步驟一:用隨機數發生器產生隨機數k∈[1,n-1];
步驟二:在ld坐標下計算橢圓曲線點c1=[k]g=(x1,y1),將c1的數據類型轉換為比特串;
對於步驟二,通過如下步驟來實現:
步驟(1):設需要存儲的點的個數r>1,g1=g,g2=[2]g1;
步驟(2):i從1增加到r-1計算g2i+1=c2i-1+g2,(i為控制循環的中間計算量,)步驟(3):naf(k)=(ki-1,,ki-2,k1,k0);(其中ki為隨機數k的從右數第i+1位,正整數k的寬度為w的);
步驟(4):令j=l-1,c1=o;當j≥0時;
(1)若kj=0,則c1=[2]c1,j=j-1;
(2)否則:
(2.1)令t是使且kt=1或k=-1的最小整數;
(2.2)
(2.3)如果hj>0,否則
(2.4)令j=t-1;(其中j,t,hj,等都是計算的中間量,l為寬度為w的naf的長度);
步驟(5):輸出c1;
步驟(6):設是y1,從最左邊到最右邊的比特;
設mk-1;mk-2;···;m0是m從最左邊到最右邊的字節,則其中0≤i<k,當8i+j≥m,01,pb1=pb,(pbi為中間量)
步驟(2):i從1增加到r-1計算
步驟(3):naf(h)=(hi-1,hi-2,h1,h0);
步驟(4):令j=l-1,s=o;當j≥0時;
(1)若hj=0,則s=[2]s,j=j-1;
(2)否則:
(2.1)令t是使且ht=1或ht=-1的最小整數;
(2.2)
(2.3)如果kj>0,否則
(2.4)令j=t-1;
步驟(5):輸出s;
步驟四:計算橢圓曲線點s1=[k]pb=(x2,y2),將坐標x2、y2的數據類型轉換為比特串;步驟四的過程按照以下步驟計算:
步驟(1):設需要存儲的點的個數r>1,pb1=pb,
步驟(2):i從1增加到r-1計算
步驟(3):naf(k)=(ki-1,,ki-2,k1,k0);
步驟(4):令j=l-1,s1=o;當j≥0時;
(1)若kj=0,則s1=[2]s1,j=j-1;
(2)否則:
(2.1)令t是使且kt=1或kt=-1的最小整數;
(2.2)
(2.3)如果hj>0,否則
(2.4)令j=t-1;
步驟(5):輸出s1;
關於對坐標x2、y2的數據類型轉換為比特串的計算通過以下步驟來實現:
步驟(1):設是y2,從最左邊到最右邊的比特;
設mk-1;mk-2;···;m0是m從最左邊到最右邊的字節,則其中0≤i<k,當8i+j≥m,0<j≤7時,其中y2,為長度為m的比特串。m為長度為k的字節串,
設mk-1,mk-2,…,m0是s從最左邊到最右邊的字節;
設是c2從最左邊到最右邊的比特,則是mj右起第i-8j+1比特,其中其中輸入m為長度為k的字節串。輸出c2為長度為m的比特串,其中m=8k。
步驟五:計算t=kdf(x2∥y2,klen),若t為全0比特串,則返回步驟一;
步驟六:計算c2=m⊕t;
步驟七:計算c3=hash(x2∥m∥y2);
步驟七的過程由以下步驟來完成:
步驟(1):令m=x2∥m∥y2;首先將比特「1」添加到消息的末尾,再添加k個「0」,其中k是滿足l+1+k=448mod512的最小的非負整數,m的長度為k比特。
步驟(2):再添加一個64位比特串,該比特串是長度l的二進位表示;[0061]步驟(3):將消息分組b(is)劃分為16個字w0,w1,…,w15。
步驟(4):從j=16到j=67循環,
wj←p1(wj-16⊕wj-9⊕(wj-3<<15))⊕(wj-13<<7)⊕wj-6
步驟(5):從j=0到j=63循環,
w』j←wj⊕wj+4;
步驟(6):令a,b,c,d,e,f,g,h為字寄存器,ss1,ss2,tt1,tt2為中間變量;
步驟(7):壓縮函數vi+1=cf(v(i),b(i)),0≤i≤n-1;
步驟(8):abcdefgh←v(i),「←」為左向賦值運算符
步驟(9):從j=0到j=63循環;
ss1←((a<<12)+e+(tj<<j))<<7
ss2←ss1⊕(a<<12)
tt1←ffj(a,b,c)+d+ss2+w』j
tt2←ggj(e,f,g)+h+ss1+wj
d←c
c←b<<9
b←a
a←tt1
h←g
g←f<<19
f←e
e←p0(tt2)
v(i+1)←abcdefgh⊕v(i)
步驟(10):對m』按512比特進行分組:m』=b(0)b(1),…,b(n-1)其中n=(l+k+65)/512。
步驟(11):從i=0到j=n-1循環,v(i+1)=cf(v(i),b(i))
其中cf是壓縮函數,v(0)為256比特初始值iv,b(i)為填充後的消息分組,迭代壓縮的結果為v(n)
步驟(12):abcdefgh←v(n),輸出256比特的雜湊值y=abcdefgh.
不同坐標系下,點加和倍點運算的複雜度見表1,因此在ld坐標系下計算點加和倍點複雜度最小,點乘運算速度最快。
表1
使用sm3密碼雜湊算法進行計算,這個步驟主要包括頂層模塊、controller控制器、消息擴展模塊、消息壓縮模塊以及結果讀取模塊如圖3所示。其中,控制模塊採用標準的三段式fsm結構設計,控制其他模塊電路的執行;消息擴展模塊主要生成相應的132個字,供後續算法壓縮電路模塊使用;消息壓鎖模塊主要實現消息的壓縮,並最終得到相應的256位加密哈希值;結果讀取模塊主要實現從256位的結果寄存器中,以32位形式讀取與輸出。同時,由於寄存器會帶來大量的面積和功耗開銷,所以為了進一步降低功耗的開銷,使用寄存器復用的方法,儘量優化並減少了寄存器的個數。通過調度優化,使得擴展和壓縮模塊的進程是可以嵌套的,這樣擴展和壓縮模塊即可共用同一個控制器產生的控制信號,這樣既減少了控制電路的複雜度,也降低了控制電路的開銷。
雖然本發明披露如上,但本發明並非限定於此。任何本領域技術人員,在不脫離本發明的精神和範圍內,均可作各種更動與修改,因此本發明的保護範圍應當以權利要求所限定的範圍為準。
