一種適用於多道次壓縮的本構模型的建立方法與流程

2023-12-07 02:35:21 3

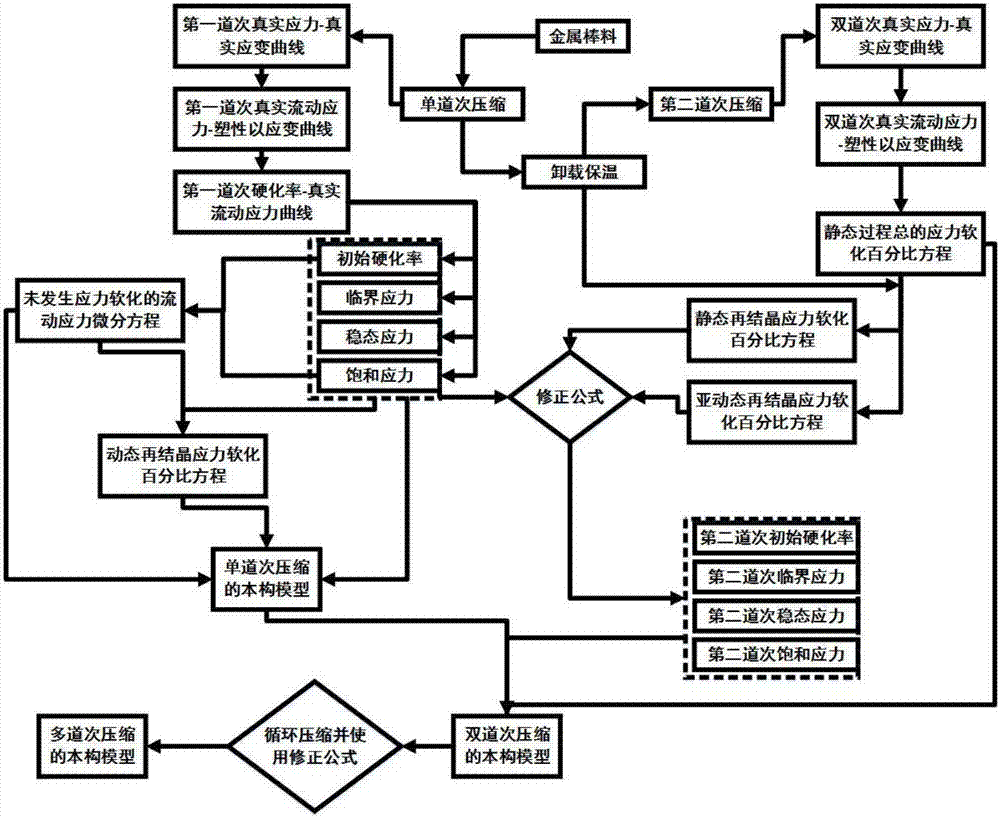
本發明屬於塑性成形的數值分析領域，更具體地，涉及一種基於應力軟化預測多道次成形中的流動應力的方法。

背景技術：

材料的本構模型是指材料在加載過程中流動應力隨著等效塑性應變的變化規律。目前常見本構模型分為兩種，唯像型和物理基本構關係。唯像型本構關係是指，採用數值分析或神經網絡的方法，分析不同變形條件下流動應力軟化和硬化行為與累計塑性應變的關係，建立的一種基於宏觀物理變量的函數關係，如變形溫度，應變速率和塑性應變等。而物理基本構關係是建立在位錯密度，彌散顆粒，細晶，晶界和形核等可測量的微觀物理量基礎上，推導內部應力和微觀組織演變的關係，並利用可測量的宏微觀變量描述材料整體的流動應力的函數。唯像型本構關係相對物理基簡單，卻無法描述發生複雜再結晶行為時的流動應力，而物理基本構關係卻過於複雜，無法直接應用於實際的大型複雜零件的工業生產，因此將兩種本構關係相結合的本構模型對大型模鍛件的成形質量的提升有重要的指導意義。在大型構件的模鍛領域，多道次熱成形工藝已經成為了最主要的成形手段。它既包含了材料進行加載的變形過程，如自由鍛，制坯和預鍛等，還包括變形道次之間的等溫熱處理過程，以提高最終成形工件的整體力學性能和合格率，整個過程遵循等體積法。

近些年來，研究學者採用物理基和唯像型本構關係對單道次的熱變形過程中流變行為建立了大量的模型，並發現準確的本構模型對於實際的工業生產和數值模擬都有巨大的作用。多道次壓縮過程是一種典型的「加載-卸載保溫-加載」的塑性成形工藝，由於存在卸載過程，累計塑性應變無法適用於整個工序。除此之外，整個工序涉及了複雜的再結晶行為及其引起的應力軟化，包括加載過程中發生的動態再結晶以及卸載保溫過程中的靜態再結晶和亞動態再結晶。因此，建立一種獨立於累計應變，適用於多道次壓縮過程的物理基和唯像型結合的本構模型對於分析材料變形特徵，材料流動和數值模擬優化成形工藝具有重要意義。

技術實現要素：

針對現有技術的以上缺陷或改進需求，本發明提供了一種預測多道次成形中的流動應力的方法，其目的在於針對前述問題，提供一種測定多道次壓縮過程中的本構模型的方法，適用於不同的溫度、應變速率、卸載應變和保溫時間等實際變形條件下的本構模型預測，解決現有技術存在的多道次壓縮帶來再結晶引起的應力軟體對原有本構模型的影響問題。

本發明提出的一種適用於多道次壓縮的本構模型的建立方法包括如下步驟：

一種適用於多道次壓縮的本構模型的建立方法，其特徵在於，包括如下步驟：

(1)根據e-m位錯密度模型和泰勒公式，並基於熱壓縮模擬試驗機上獲得的單道次壓縮實驗的應力應變關係，也可利用已有的實驗結果，，獲得金屬壓縮棒料在單道次壓縮過程中的動態再結晶軟化百分比模型，並以此計算單道次壓縮過程中獨立於累計塑性應變的本構模型；

(2)在熱壓縮模擬試驗機上再次進行壓縮實驗，獲得多道次壓縮實驗的應力應變關係；控制卸載應變和保溫時間，獲得材料靜態再結晶和亞動態再結晶的軟化百分比模型(公式(3))；所述多道次壓縮實驗包括「變形-保溫-變形」的過程；

(3)根據步驟(2)中獲得不同卸載應變和保溫時間條件下的總軟化百分比，對步驟(1)中的本構模型進行修正，修正其初始硬化率和應力內變量的值，即，使其適用於多道次壓縮過程；

重複步驟(1)-(3)，得到多道次壓縮過程中獨立於累計應變的唯像型和物理基結合的本構模型，即微觀的計量值和宏觀的應力大小結合。

優選地，所述步驟(1)動態再結晶的軟化百分比模型和單道次壓縮過程中獨立於累計應變的本構模型的建立方法包括以下幾個子步驟：

(1-1)取符合國標的壓縮棒料，在不同溫度和應變速率條件下，進行單道次壓縮實驗，得到工程應力-工程應變曲線，將其轉化為不同溫度和應變速率條件下的真實應力-真實應變曲線；

(1-2)在得到的各真實應力-真實應變曲線上，獲得該曲線的屈服應力σ0，即不同溫度和應變速率條件下的屈服應力；將該曲線減去屈服應力對應的真實應變，實現屈服應變清零，獲得真實流動應力-真實塑性應變曲線(流應曲線)；對流應曲線的真實塑性應變求導，得到硬化率θ-真實塑性應變曲線；根據硬化率θ-真實塑性應變曲線，採取坐標變換方法，得到硬化率θ-真實流動應力曲線(θ-σ曲線)；

(1-3)利用所述θ-σ曲線，得到該曲線的初始硬化率θ0(屈服應力對應的硬化率為初始硬化率，屈服應力對應的應變速率從θ-σ曲線中可以讀出，已知屈服應力，對應的硬化率θ-就可以知道)，臨界應力σcd，飽和應力σsat和穩態應力σs；所述臨界應力σcd是指動態再結晶開始發生時的臨界應力，表徵為θ-σ曲線上拐點所對應的流動應力值；飽和應力σsat是指當不存在應力軟化時最終流動應力的漸進值(也稱收斂值，指當橫標趨近於無限大時，流動應力的大小趨向一個常數數值)，表徵為θ-σ曲線拐點處的切線與流動應力軸的交點對應的流動應力值；穩態應力σs是指當發生動態再結晶造成應力軟化時最終(時間足夠大條件下)流動應力的漸進值，表徵為θ-σ曲線與流動應力軸的第一個交點對應的流動應力值；根據e-m位錯密度模型和泰勒公式，得到任意時刻t下沒有發生應力軟化的流動應力σr的函數：

(1-4)根據子步驟(1-3)得到的任意時刻t下沒有發生應力軟化的流動應力σr和子步驟(1-2)得到的硬化率θ-真實流動應力曲線曲線(θ-σ曲線)，計算獲得各曲線任意時刻t的動態再結晶應力軟化百分比xd；

聯立公式(2)、(3)、(4)，採用非線性回歸方法，求出再結晶速度相關的常數kv和動態再結晶發生50％所需的時間(曲線可以讀出或測量得到)，晶粒大小相關的常數d(可通過對上述的xd-t曲線非線性回歸計算)，得到溫度相關的指數q，熱成形過程中的變形激活能qd，動態再結晶的表面激活能qdrx；q、qd和qdrx為材料固有參數；公式(3)、(4)如下：

其中，式中，tc表示再結晶發生的時間為臨界應力σcd對應的時間，r為摩爾氣體常數，t為當前時刻的溫度；所述臨界應力σcd是指動態再結晶開始發生時的應力；

(1-5)根據公式(1)、(2)、(3)、(4)，得到材料獨立於累計塑性應變的流動應力σ的函數關係式，即微分方式表達的本構模型：

優選地，所述步驟(2)所述靜態再結晶和亞動態再結晶的軟化百分比模型的建立方法包括以下幾個子步驟：

(2-1)取步驟(1)中相同的壓縮棒料，在與步驟(1)相同的應變速率和溫度條件下，進行單道次壓縮實驗後，隨後卸載保溫一定時間到不再發生結晶後，取不同溫度和應變速率再次進行壓縮實驗，得到多道次工程應力-工程應變曲線，將其轉化為不同溫度和應變速率條件下的真實應力-真實應變曲線；各次壓縮中，第一次變形量(相對於原始長度變形率)範圍取正常國標壓縮試樣的範圍10％-80％(為了計算得出公式(8)的結果，至少取六個前道次卸載應變)，其餘道次壓縮的變形量範圍取15％-35％；各道次應變速率範圍和溫度範圍為0.01-10s-1,1173k-1423k；得到獲得多道次壓縮過程中材料的流應曲線；

(2-2)根據子步驟(2-1)中的各流應曲線計算第一道次壓縮的卸載應力值σm，即曲線中第一次驟降的點對應的應力值，可以直接從圖上讀出；多道次壓縮中第一次壓縮的彈性階段直線偏移2％(沿著橫坐標向右平移2％)與在前道次流應曲線的交點σ2％，在後一道次壓縮中壓縮的彈性階段直線偏移2％與流應曲線的交點σ′2％，根據下式計算卸載保溫過程中各流應曲線對應的總應力軟化百分比xst並繪製不同卸載應變條件下的xst-t曲線：

其中，所述xst包括靜態再結晶造成的應力軟化百分比xs和亞動態再結晶造成的應力軟化百分比xm；

(2-3)採用下式，計算i機制(表示材料受到的軟化機制，包括靜態再結晶和亞動態再結晶兩種)下保溫時間為t時的應力軟化百分比xi，

其中，i機制下應力軟化百分比時間常數ni和造成的應力軟化百分比達到50％所需的時間是根據子步驟(2-2)中獲得的各xst曲線，採用非線性回歸分析得出卸載保溫過程中的再結晶造成的應力軟化方程後，求出當保溫時間足夠長(再結晶完全完成)時得到的；優選的，所述xst可表示為靜態再結晶軟化和亞動態再結晶軟化百分比之和，如公式(8)所示，以下的材料參數ni和都是通過對xst-t曲線進行非線性回歸計算獲得。

其中xm∞，nm和t50m是亞動態再結晶機制的應力軟化百分比、時間常數和應力軟化百分比達到50％所需的時間，其中xs∞，ns和t50s是靜態再結晶機制的應力軟化百分比、時間常數和應力軟化百分比達到50％所需的時間。

優選地，步驟(3)包括以下子步驟：

(3-1)將步驟(1-2)和(1-3)中獲得的各個參數θ0，σcd，σsat、σs和σ0，將公式(3)、(4)，代入公式(5)，求出前道次壓縮過程中的獨立於累計塑性應變的流動應力曲線。(3-2)利用子步驟(2-2)中的公式(7)，和子步驟(2-3)中的公式(8)，獲得後一道次壓縮之前的總軟化百分比xst(計算方法是非線性回歸計算的，採用的為經典的艾倫尼烏斯公式，擴散動力學模型)，對(3-1)所述的各個參數σcd，σsat、σs和σ0逐一採用公式(9)進行修正；σj和σj′分別代表修正前後的σcd，σsat、σs和σ0；

σ′j＝(1-xst)*(σm-σ2％)+σj(9)

然後，將初始硬化率θ0校正為後一道次的初始硬化率θ′0，θ′0為第一道次壓縮過程中的θ-σ曲線上σm對應的硬化率；

(3-3)利用子步驟(3-2)中獲得的修正後的參數θ′0，σ′cd，σ′sat，σ′s，σ′0和步驟(2-2)計算獲得的xst以及後一道次壓縮實驗獲得的公式(3)和(4)，代入公式(5)，求出後一道次壓縮過程中的獨立於累計塑性應變的流動應力曲線；

(3-4)依次類推，理論上可以推無窮次，但是這裡限制為材料斷裂之前都可以使用本模型推導，優選取4-5次，在步驟(3-3)獲得後一道次壓縮的本構模型的基礎上，利用公式(7)和(8)的獲得n道次壓縮之前(n>2)的總軟化百分比xst對(3-2)中獲得的各個矯正後的參數θ′0，σ′cd，σ′sat，σ′s，σ′0進行進一步矯正，將矯正後的上述參數代入公式(5)，得到多道次壓縮過程的本構模型。

總體而言，通過本發明所構思的以上技術方案與現有技術相比，由於發明內容結合和唯像型和物理基本構模型，能夠取得下列有益效果。

1)本發明的本構模型和實際工藝過程相符：由於採用了單道次壓縮過程和雙道次壓縮過程中的流應曲線，與新型動態再結晶動力學模型和再結晶應力軟化模型相結合的方法，建立了唯像型和物理基耦合的獨立於累計塑性應變的本構模型，既能反應材料在多道次壓縮過程中的微觀組織演變，也能描述宏觀的材料流動行為，因此使用本發明的本構模型與實際的工藝過程相符。

2)本發明的本構模型較為準確適用範圍廣：通過實際檢測證明，該方法不僅適用於不同溫度和應變速率條件下的單道次壓縮過程，而且適用於不同卸載應變和保溫時間條件下的雙道次壓縮過程。除此之外，還能普及到實際的多道次成形過程，並適用於數值模擬優化成形工藝。

3)本發明的本構模型預測結果準確：與抽樣的條件下的實驗結果對比發現，本發明的本構模型與單道次壓縮實驗結果的相關性係數為0.9998，平均相對誤差為6.3％，絕對誤差在±10mpa內；與雙道次壓縮實驗結果的相關性係數為0.9884，平均相對誤差為3.63％，絕對誤差在±10mpa內。因此本發明的是一種可靠可信的數值方法，該本構模型的流動應力預測值十分準確。

附圖說明

圖1示出本發明的本構模型建立方法的流程圖；

圖2示出單道次壓縮和雙道次壓縮的工藝流程圖；

圖3示出各個應力參數在流應曲線上的定性表徵；

圖4示出隨機抽取的單道次壓縮中流動應力實驗值和使用本發明的方法獲得的預測值的對比；

圖5示出隨機抽取的雙道次壓縮中第二次流應的實驗值和使用本發明的方法獲得的預測值對比。

具體實施方式

為了使本發明的目的、技術方案及優點更加清楚明白，以下結合附圖及實施例，對本發明進行進一步詳細說明。應當理解，此處所描述的具體實施例僅僅用以解釋本發明，並不用於限定本發明。此外，下面所描述的本發明各個實施方式中所涉及到的技術特徵只要彼此之間未構成衝突就可以相互組合。

以300m高強鋼的多道次壓縮過程中的本構模型為實例說明本發明。具體流程如圖1所示。

1)將300m高強鋼製成φ8mm×10mm的標準壓縮件，單道次壓縮實驗是在gleeble-3500熱機模擬試驗機上進行的，具體工藝過程參見圖2。在單道次熱壓縮試驗過程中，試樣首先以5k/s加熱到1423k，保溫240s以保證試樣內部微觀結構完全奧氏體化，其次在熱電偶的控制下，以-1k/s的冷卻速度將溫度控制在1173k-1423k之間(等差選擇6個溫度)，選擇的溫度並保溫120s確保試樣內部溫度均勻，隨後分別0.01，0.1，1，10s-1的應變速率進行等溫壓縮實驗，當試樣壓縮量到達60％時，在真空的環境中試樣自動水淬。根據以上的實驗得出24條工程應力-工程應變曲線，將所有曲線變換為真實應力-真實應變曲線。

2)取所述的不同溫度和應變速率條件下的曲線，分別將彈性階段的直線向右平移0.2％，獲得對應變形條件下的屈服應力σ0，並將所述的曲線轉化為流應曲線。除此之外，對流應曲線進行差分計算，繪製對應變形條件下的θ-σ曲線。

3)在所述中不同溫度和應變速率的θ-σ曲線上，計算對應的初始硬化率θ0，臨界應力σcd，飽和應力σsat，穩態應力σs，相關的表徵如圖3所示，將所述的屈服應力σ0和上述的參數代入公式(1)，利用runge-kutta法求出σr在任意時刻的值，繪製24個σr-t曲線。

4)利用所述的任意時刻的σr和所述的流應曲線，計算獲得1173k-1423k和0.01-10s-1變形條件下的動態再結晶應力軟化百分比xd在任意時刻的值。

5)根據所述的xd，繪製xd-t曲線。對所有的xd-t曲線採用非線性回歸分析方法獲得新型動態再結晶造成的應力軟化百分比模型，其中材料常數kv為-3.9475，d為1.81e-3，q為-0.99，r為8.314，變形激活能qd為359mpa，動態再結晶的表面激活能qdrx為412mpa，以上的參數均是非線性回歸計算獲得。

6)對所述的公式(1)和所述的動態再結晶的應力軟化模型計算，獲得獨立於累計塑性應變的流動應力σ的差分函數。

7)雙道次壓縮實驗是在gleeble-3500熱模擬實驗機上進行的。在雙道次壓縮過程中，首先在1173k和1273k的溫度，0.01s-1和10s-1的應變速率四種組合的變形條件下，進行單道次壓縮實驗，第一次變形量分別為8％，14％，20％，25％，30％，40％和50％，隨後卸載保溫一定時間，保溫時間包括0s，5s，10s，50s，120s，200s和600s，最後繼續壓縮25％的變形量後水淬。利用步驟1)的方法計算獲得雙道次壓縮過程中流應曲線。

8)選取1273k和0.01s-1的變形條件為例計算雙道次壓縮中的應力軟化行為，對步驟7)中的流應曲線採用2％的應變偏移法計算卸載保溫過程中總的應力軟化百分比xst。

9)在1273k和0.01s-1的變形條件下，將步驟8)獲得的xst繪製49條xst-t曲線，對所有曲線採用非線性回歸分析計算出公式(7)和公式(8)中的各個參數，獲得卸載保溫過程中的靜態再結晶和亞動態再結晶造成的應力軟化模型。靜態再結晶和亞動態再結晶的常數ni值分別為1.63和1.49。

10)將步驟3)中獲得的各個參數θ0，σcd，σsat和σs，步驟2)獲得的σ0，以及步驟5)獲得的動態再結晶動力學模型代入公式(5)，並採用runge-kutta法計算，獲得第一次壓縮過程中不同溫度和應變速率的24種變形條件下，受到動態再結晶造成的應力軟化影響卻獨立於累計塑性應變的流動應力。隨機抽取的單道次壓縮中流動應力實驗值和使用本發明的方法獲得的預測值的對比參見如圖4，其中相關性係數為0.9998，平均相對誤差為6.3％，絕對誤差在±10mpa內，本發明的本構模型的吻合度較高。

11)在1273k和0.01s-1的變形條件下，對於49種卸載應變和保溫時間組合，採用步驟9)中獲得的卸載保溫過程中總的應力軟化百分比xst，首先通過公式(9)將步驟2)和步驟3)中的應力參數σi矯正為第二道次壓縮的應力參數σi′，然後將第二道次的初始硬化率θ0′表示為第一道次壓縮過程中的θ-σ曲線上σm處對應的硬化率，最後，用矯正後的參數θ0′和σi′代入公式(5)，並採用runge-kutta法計算，獲得不同變形條件下，第二次壓縮過程中基於應力軟化而獨立於累計應變的流動應力值。雙道次壓縮中第二次流應的實驗值和使用本發明的方法獲得的預測值對比如圖5，其中相關性係數為0.9884，平均相對誤差為3.63％，絕對誤差在±10mpa內，本發明的本構模型的吻合度較高。

總體看來，本發明的一種適用於多道次壓縮過程獨立於累計應變的本構模型的建立方法是一種可靠，可行的數值分析方法，該方法可以用於提高了大型模鍛件的產品質量和數值模擬優化成形工藝等領域。

本領域的技術人員容易理解，以上所述僅為本發明的較佳實施例而已，並不用以限制本發明，凡在本發明的精神和原則之內所作的任何修改、等同替換和改進等，均應包含在本發明的保護範圍之內。