一種RSD晶片電流密度分布計算方法與流程
2023-10-20 03:46:57 2
本發明屬於半導體開關技術領域,涉及一種rsd晶片電流密度分布計算方法。
背景技術:
脈衝功率技術是把相對長時間內存儲的具有較高密度的能量,以單次脈衝或重複頻率的短脈衝方式釋放到負載上的電物理技術。廢氣處理等環保需求推進了重複頻率脈衝功率技術以及半導體脈衝開關的發展。其中,晶閘管主要應用於毫秒及以上脈衝寬度ka級電流應用領域,igbt主要應用於微秒脈衝中等功率脈衝電源。這些半導體功率開關的主要缺點不能同時滿足電流上升率(di/dt)高、電流峰值大、輸出電壓高等要求。
20世紀80年代,前蘇聯院士i.v.grekhov發明的反向開關電晶體(reverselyswitcheddynistor,rsd)採用可控等離子體層觸發方式,反向注入觸發電流,在整個晶片面積上實現了同步均勻導通,可以實現高di/dt大電流微秒開通。基於rsd的重複頻率脈衝功率電源在環境保護、食品保鮮、軍事、工業加工等領域有著廣泛的應用前景。rsd器件是一種由數萬個晶閘管與電晶體元胞相間並聯排列的器件,沒有普通晶閘管的控制極,採用可控等離子體層觸發方式,反向注入觸發電流,在整個晶片面積上實現了同步均勻導通,從器件原理上消除了普通晶閘管器件存在的開通局部化現象,可以實現高di/dt微秒開通,同時在短時間內通過很大的電流。特殊的結構及開通原理使得rsd具有如下特點:全面積同步均勻導通;高功率微秒換流;理論上可無限串並聯;串並聯使用時觸發電路結構簡單;晶片面積利用率高;使用壽命長。
在rsd晶片的加熱、降溫、摻雜等生產過程中,由於工藝條件分布不均勻,使rsd晶片內部的半導體參數分布不一致,導致實際物理實驗過程中,rsd晶片內部的電流密度分布可能存在不均衡的情況。現有的rsd器件仿真模型及方法將rsd簡化為一個晶閘管單元和一個電晶體單元的反並聯組合,並按照經典計算公式進行仿真。這種方法的計算前提是假設整個rsd晶片內部的電流密度分布均勻,且只能進行器件的原理性仿真,無法模擬整個rsd晶片的電流分布情況,現有的實驗測試條件也不能測量整個rsd晶片的電流分布情況,不利於rsd的研究和發展。
技術實現要素:
本發明的目的是針對現有的技術存在的上述問題,提供一種rsd晶片電流密度分布計算方法,本發明所要解決的技術問題是如何對rsd晶片電流密度分布進行計算。
本發明的目的可通過下列技術方案來實現:一種rsd晶片電流密度分布計算方法,其特徵在於,本計算方法為離散化方法,其方法步驟如下:
步驟一、從rsd取出寬度為h、長度為rsd晶片直徑d的部分晶片;
步驟二、將步驟一所述部分晶片離散化為n個小rsd單元排成單列;
步驟三、將步驟二所述小rsd單元內部按照理想器件處理,即內部的wn參數分布完全一樣,預充及正嚮導通電流密度分布均勻;
步驟四、所述小rsd單元的電流計算公式:rsd脈衝放電電路的主迴路參數如下:迴路總電感為l,放電電容為c0,迴路總電阻為r,u為電容c0的電壓,主迴路電流,計算
式中,預充階段的電壓及電流密度計算:rsd電壓降
式中,qn=qndwn,採用梯形法計算積分qr(t)|t=(n+1)dt,代入式(2),方程變換為以jf(t)為自變量的二元一次方程,求解得到n個小rsd單元的總電流:
式中,d=(bqn)-1-(bqn)-2qr(t)|t=ndt/3,e=(bqn)-2dt/3,v=ur|t=(n+1)dt,arsd為小rsd單元的面積,j|t=(n+1)dt為t=(n+1)dt時刻的電路方程計算得到的rsd晶片總電流密度;正嚮導通階段的rsd單元電壓及電流密度計算:磁開關飽和後,rsd電壓降
式中,
正嚮導通後,rsd電壓降
式中,
t=(n+1)dt時,整理得到
式中,採用梯形法計算積分qf(t),(6)變換為以jf(t)為自變量的二元一次方程,求解得到n個小rsd晶片的總電流密度:
,其中,p(x,t)為剩餘等離子體的濃度,ndn為基區的摻雜濃度,b=μn/μp為弱電場中電子與空穴遷移率的比值,j(t)為流過等離子體電流的密度,wnn為基區寬度。
步驟五、步驟四中所述非線性方程(3)和(7)採用近似牛頓法求解。
在上述技術方案中,每個小rsd的工藝參數wn根據仿真需要獨立設置數值。
在上述的一種rsd晶片電流密度分布計算方法中,所述離散化方法為均勻有限差分法。
根據研究目的不同,半導體功率開關晶片(器件)的模型分為工藝模型、物理模型、電學模型三種。
工藝模型採用工藝規範參數作為基本仿真參數,包括工藝流程中的溫度、處理時間、擴散雜質的濃度等。模型的精確度是最高的,但也是最複雜的,主要用於器件結構改進、新結構設計、工藝參數最優化的仿真,很少用於電路的仿真。
物理模型將晶片的輸入輸出參數與物理結構和拓撲參數相聯繫,其基本參數是器件的幾何尺寸和物理參數,包括雜質濃度的空間分布、少數載流子壽命及載流子遷移率等。並利用描述半導體物理電特性的基本方程,如決定靜電勢的二維泊松方程、決定電子和空穴濃度的電流連續方程和電流密度方程等,進行建模。這些偏微分方程的可直接計算的解析式一般很難推導得到,因此,多採用數值計算的方法求出所研究區間的某些點函數的近似值,當計算的點足夠密時,數值計算結果就是開關實際物理過程的描述。實際中最常用的方法是有限元法和有限差分法。有限元法是將待求解區域劃分為很多子單元,以單元組合而成的結構近似替代原連續結構,通過對子區域的差值求解來逼近真實解。有限差分法將偏微分方程離散化,在各離散區域用差分方程代替微分方程進行計算。常用器件仿真軟體有模擬器件穩態和暫態特性的pisces,及用於對高壓和功率器件進行數值分析的geds。
電學模型只考慮主要的輸入和輸出的電壓電流特性,同時將半導體功率開關理想化,即假設器件的內部結構均勻,器件內部的傳輸時間忽略不計。模型的原始參數為器件放大係數、跨導、輸入輸出阻抗等。這種模型既能足夠精確的反映器件的輸入輸出特性,計算又相對簡化,因此多用於電路仿真、設計。電學模型可分為基本模型、子電路模型、數學模型三種。
本專利基於物理模型,建立rsd晶片的二維電流密度分布計算模型。
rsd器件的離散化方法:
半導體器件的離散化方法通常採用有限差分、有限箱或者有限元法。三種差分化方法也分布對應了不同網格化方法,對編寫程序的複雜度和計算機運算量的要求存在較大的差別。
有限差分法用相互垂直的網格線將整個器件劃分為大量的方形區域。當網格較密時,格點處的微分便可直接通過前向差分、後向差分或者中心差分的方法通過相鄰格點獲得。當相互垂直線距相等時便是均勻有限差分法,否則為非均勻有限差分法。為了得到較為精確的結構有限差分法劃分出來的網格中通常會存在很多不必精確計算的點,產生了大量的不必要的計算。為了避免這些不必要的計算,在網格劃分的時候去除部分不需要的格點,這便是有限箱法。有限元法通過求解一個與原偏微分方程邊值問題相聯繫的一個泛函取極限值所對應的方程的解,從而獲得原方程邊值問題的解。有限元法的網格選取和增補比較靈活(可採用三角形或多邊形網格劃分),其主要缺點是算法太複雜,計算工作量大。
非線性方程(3)、(7)的求解方法主要有二分法、牛頓法、近似牛頓法等。二分法算法簡單,但收斂速度較慢;牛頓法利用泰勒展開的方法在已知格點處將非線性方程組轉化為具有線性關係的方程組,從而通過線性方程組的迭代求解逼近原非線性方程解,具有收斂速度快,計算精確等優點,但要求被求函數可導,還必須求出函數導數的解析式,但很多函數很難或無法得到導數的解析時,因此牛頓法的應用範圍有局限;近似牛頓法用一個近似算式代替函數導數的解析式,收斂速度也很快,不要求函數可導,應用範圍非常廣。本專利採用近似牛頓法求解(3)、(7)。
本發明rsd晶片電流密度分布計算方法及仿真模型,具有以下有益效果:有效解決了基於工藝條件和現有實驗測試條件,無法預測和驗證rsd晶片內部電流密度分布情況的問題,所述方法工藝簡單、易操作,本發明可廣泛應用於半導體器件、集成電路等領域。
附圖說明
圖1為本發明rsd晶片電流密度分布計算方法中的rsd晶片二維模型網格劃分示意圖;
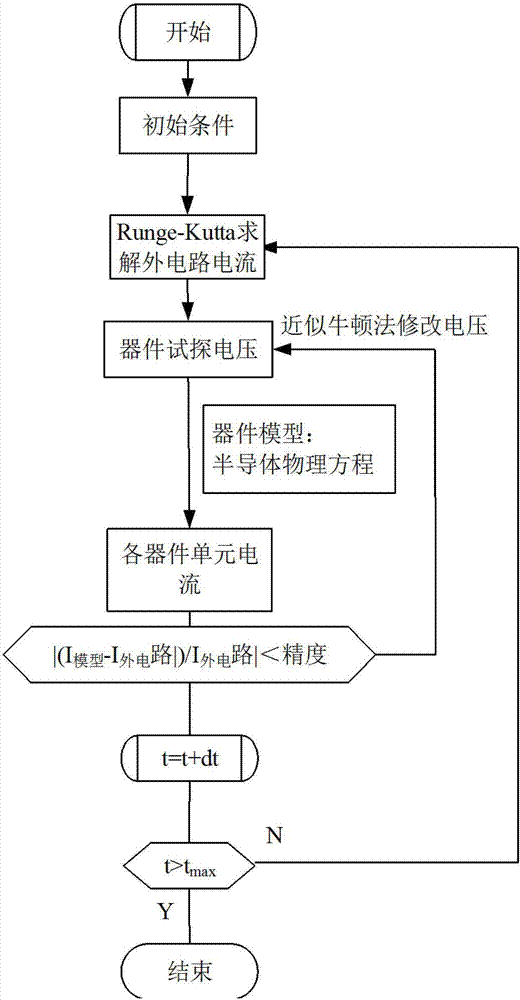
圖2為本發明rsd晶片電流密度分布計算方法的流程示意圖。
具體實施方式
以下是本發明的具體實施例並結合附圖,對本發明的技術方案作進一步的描述,但本發明並不限於這些實施例。
下面結合附圖及實施例對本發明作進一步的詳細描述,但該實施例不應理解為對本發明的限制。
本發明rsd晶片電流密度分布計算方法,所述的方法為離散化方法,其方法步驟如下:
步驟一、從rsd取出寬度為h、長度為rsd晶片直徑d的部分晶片;
步驟二、參見圖1,將步驟一所述的部分晶片離散化為n個小rsd單元排成單列;
步驟三、將步驟二所述的小rsd單元內部按照理想器件處理,即內部的wn參數分布完全一樣,預充及正嚮導通電流密度分布均勻;
步驟四、所述小rsd單元的電流計算公式:
rsd脈衝放電電路的主迴路參數如下:迴路總電感為l,放電電容為c0,迴路總電阻為r,u為電容c0的電壓,主迴路電流,
式中,
預充階段的電壓及電流密度計算:
rsd電壓降
式中,qn=qndwn,
採用梯形法計算積分qr(t)|t=(n+1)dt,代入式(2),方程變換為以jf(t)為自變量的二元一次方程,求解得到n個小rsd單元的總電流:
式中,d=(bqn)-1-(bqn)-2qr(t)|t=ndt/3,e=(bqn)-2dt/3,v=ur|t=(n+1)dt,arsd為小rsd單元的面積,j|t=(n+1)dt為t=(n+1)dt時刻的電路方程計算得到的rsd晶片總電流密度;
正嚮導通階段的rsd單元電壓及電流密度計算:
磁開關飽和後,rsd電壓降
式中,
正嚮導通後,rsd電壓降
式中,
t=(n+1)dt時,整理得到
式中,採用梯形法計算積分qf(t),(6)變換為以jf(t)為自變量的二元一次方程,求解得到n個小rsd晶片的總電流密度:
其中,
p(x,t)剩餘等離子體的濃度,
ndn基區的摻雜濃度,
b=μn/μp弱電場中電子與空穴遷移率的比值,
j(t)流過等離子體電流的密度,
wnn基區寬度;
步驟五、步驟四中所述的非線性方程(3)、(7)採用近似牛頓法求解。
每個小rsd的工藝參數wn根據仿真需要獨立設置數值。
所述離散化方法為均勻有限差分法。
根據研究目的不同,開關的模型分為工藝模型、物理模型、電學模型三種。
工藝模型採用工藝規範參數作為基本仿真參數,包括工藝流程中的溫度、處理時間、擴散雜質的濃度等。模型的精確度是最高的,但也是最複雜的,主要用於器件結構改進、新結構設計、工藝參數最優化的仿真,很少用於電路的仿真。
物理模型將開關的輸入輸出參數與物理結構和拓撲參數相聯繫,其基本參數是器件的幾何尺寸和物理參數,包括雜質濃度的空間分布、少數載流子壽命及載流子遷移率等。並利用描述半導體物理電特性的基本方程,如決定靜電勢的二維泊松方程、決定電子和空穴濃度的電流連續方程和電流密度方程等,進行建模。這些偏微分方程的可直接計算的解析式一般很難推導得到,因此,多採用數值計算的方法求出所研究區間的某些點函數的近似值,當計算的點足夠密時,數值計算結果就是開關實際物理過程的描述。實際中最常用的方法是有限元法和有限差分法。有限元法是將待求解區域劃分為很多子單元,以單元組合而成的結構近似替代原連續結構,通過對子區域的差值求解來逼近真實解。有限差分法將偏微分方程離散化,在各離散區域用差分方程代替微分方程進行計算。常用器件仿真軟體有模擬器件穩態和暫態特性的pisces,及用於對高壓和功率器件進行數值分析的geds。
電學模型只考慮主要的輸入和輸出的電壓電流特性,同時將開關理想化,即假設器件的內部結構均勻,器件內部的傳輸時間忽略不計。模型的原始參數為器件放大係數、跨導、輸入輸出阻抗等。這種模型既能足夠精確的反映器件的輸入輸出特性,計算又相對簡化,因此多用於電路仿真、設計。電學模型可分為基本模型、子電路模型、數學模型三種。
本專利基於物理模型,建立rsd晶片的二維電流密度分布計算模型。
rsd器件的離散化方法:
半導體器件的離散化方法通常採用有限差分、有限箱或者有限元法。三種差分化方法也分布對應了不同網格化方法,對編寫程序的複雜度和計算機運算量的要求存在較大的差別。
有限差分法用相互垂直的網格線將整個器件劃分為大量的方形區域。當網格較密時,格點處的微分便可直接通過前向差分、後向差分或者中心差分的方法通過相鄰格點獲得。當相互垂直線距相等時便是均勻有限差分法,否則為非均勻有限差分法。為了得到較為精確的結構有限差分法劃分出來的網格中通常會存在很多不必精確計算的點,產生了大量的不必要的計算。為了避免這些不必要的計算,在網格劃分的時候去除部分不需要的格點,這便是有限箱法。有限元法通過求解一個與原偏微分方程邊值問題相聯繫的一個泛函取極限值所對應的方程的解,從而獲得原方程邊值問題的解。有限元法的網格選取和增補比較靈活(可採用三角形或多邊形網格劃分),其主要缺點是算法太複雜,計算工作量大。
非線性方程(3)、(7)的求解方法主要有二分法、牛頓法、近似牛頓法等。二分法算法簡單,但收斂速度較慢;牛頓法利用泰勒展開的方法在已知格點處將非線性方程組轉化為具有線性關係的方程組,從而通過線性方程組的迭代求解逼近原非線性方程解,具有收斂速度快,計算精確等優點,但要求被求函數可導,還必須求出函數導數的解析式,但很多函數很難或無法得到導數的解析時,因此牛頓法的應用範圍有局限;近似牛頓法用一個近似算式代替函數導數的解析式,收斂速度也很快,不要求函數可導,應用範圍非常廣。本專利採用近似牛頓法求解(3)、(7)。
參見圖2,rsd器件仿真電路採用直接預充方式,具體過程如下:
一、首先建立電路的初始條件,設置各參數的數值,t為當前時刻式時間數值,初始值為0,dt為時間的增量,tmax為計算結束時間;
二、當前時刻t=t0時,採用runge-kutta法利用t0時刻電路參數值,並且認為晶片電壓ursd保持不變,計算t0+dt時刻,rsd晶片電流值irsd;
三、然後利用t0時刻的rsd晶片電壓與電流值,獲取小rsd單元初始電壓;
四、再將小rsd單元初始電壓帶入器件模型(半導體物理模型),迭代求解獲得t0+dt時刻各小rsd單元的電流值;
五、然後,根據小rsd單元電流值和外電路模型電流值,利用近似牛頓迭代法,修正外加電壓;
六、以此方法循環求解器件模型與電路模型,當器件分離單元模型和外電路模型的數值解之差小於初始條件設定的允許誤差時,結束當前時刻的電壓電流數值計算循環;
七、設置當前時刻t=t0+dt,當ttmax時,結束計算。
顯然,本領域的技術人員可以對本發明進行各種改動和變型而不脫離本發明的精神和範圍。這樣,倘若本發明的這些修改和變型屬於本發明權利要求及其等同技術的範圍之內,則本發明也意圖包含這些改動和變型在內。
顯然,本說明書中未作詳細描述的內容屬於本領域專業技術人員公知的現有技術。
