一種多信息融合的汽車質心側偏角估計方法與流程
2023-10-17 05:33:54 2
本發明涉及一種汽車質心側偏角估計方法,尤其是涉及一種多信息融合的汽車質心側偏角估計方法。
背景技術:
質心側偏角是大多數車輛側向動力學控制中輸入信息,實時估計車輛質心側偏角是車輛穩定性控制的基礎。
目前國內外車輛質心側偏角估計方法主要有:1、基於運動學模型估計方法,利用側向加速度傳感器進行直接積分得到車輛質心側偏角,但該方法嚴格依賴於傳感器信息,由於imu存在噪聲,長時間對加速度信號進行積分會導致誤差積累;2、基於車輛動力學模型估計方法,但是這類方法對模型本身的精度要求很高,同時對模型參數的變化比較敏感。3、用gps或非接觸式光學等傳感器直接測量質心側偏角,但是成本過高。
技術實現要素:
本發明的目的就是為了克服上述現有技術存在的缺陷而提供一種多信息融合的汽車質心側偏角估計方法。
本發明的目的可以通過以下技術方案來實現:
一種多信息融合的汽車質心側偏角估計方法,該方法包括如下步驟:
(1)採用運動學估計法進行估計,得到運動學質心側偏角估計值
(2)採用線性二自由度單軌車輛模型建立基於動力學的龍貝格觀測器,採用觀測器估計得到動力學質心側偏角估計值
(3)採用下述公式對和進行融合,得到質心側偏角估計值
其中,τ為濾波常數,s為拉氏算子。
步驟(1)具體包括:
(1a)實時測量車身側向加速度ay和車身橫擺角速度已知縱向車速為v;
(2a)根據下述運動學估計公式求取
其中,β0為質心側偏角初始值。
步驟(1a)中還需實時測量方向盤轉角γ,當方向盤轉角γ變化範圍在±10°以內保持5s以上,則步驟(2a)中求取時將積分項置。
步驟(2)中的線性二自由度單軌車輛模型為:
其中,cf1和cf2分別為前輪模型參數,cr1和cr2分別表示後輪模型參數,cf1、cf2、cr1和cr2均為常數,δ為前輪轉角,j為車身橫擺轉動慣量,lf和lr分別為車輛質心至前軸和後軸的距離,m為車輛質量,v為縱向車速,為車身橫擺角速度,β為動力學質心側偏角;
αf和αr分別為前輪和後輪側偏角,具體為:
對於線性二自由度單軌車輛模型,構建廣義龍貝格觀測器對β進行觀測得到觀測值,β觀測值即為動力學質心側偏角估計值
與現有技術相比,本發明具有如下優點:
(1)本發明將運動學估計和動力學估計相融合,在低頻範圍內,基於動力學方法的估計結果對最終估計結果起主要作用,此時,估計結果對傳感器偏置誤差具有較強的魯棒性,在高頻響應階段,運動學方法的估計結果起主要作用,此時,估計結果對模型誤差具有較強的魯棒性,並且對質心側偏角的動態變化估計得更準確,多信息融合估計的方法對傳感器偏差和模型誤差的魯棒性都有所加強,同時,由於該融合估計方法使用到了信號所有的頻率,因此,其估計結果的相位滯後也是最小的,估計結果更加準確可靠。
(2)本發明採用運動學估計法獲取運動學質心側偏角估計值時,以方向盤轉角信號為依據,當方向盤轉角γ在±10°以內保持5s以上,重置積分,從而實現了積分重置機制,當車輛保持較長時間直線行駛時,對積分法進行重置,以減小誤差積累,從而提高後續估計結果的準確性。
附圖說明
圖1為本發明多信息融合的汽車質心側偏角估計方法的流程框圖;
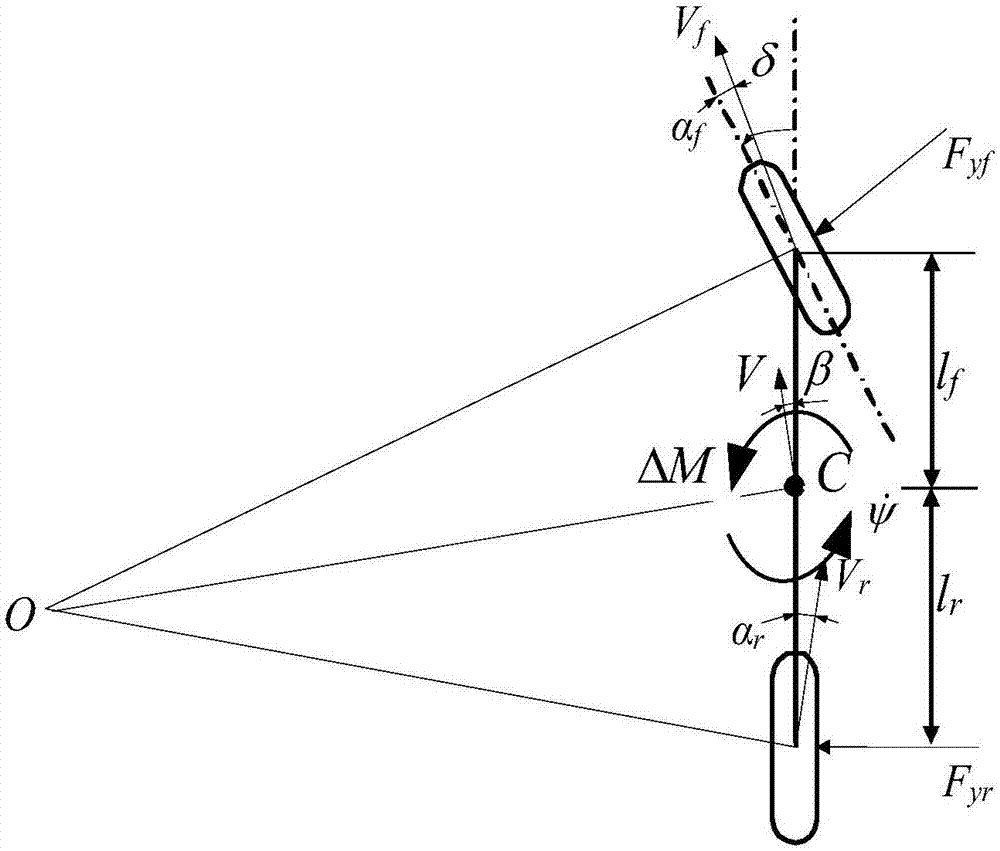
圖2為本線性二自由度單軌車輛模型結構示意圖;
圖3為本發明廣義龍貝格觀測器結構框圖。
具體實施方式
下面結合附圖和具體實施例對本發明進行詳細說明。
實施例
如圖1所示,一種多信息融合的汽車質心側偏角估計方法,該方法包括如下步驟:
(1)採用運動學估計法進行估計,得到運動學質心側偏角估計值
(2)採用線性二自由度單軌車輛模型建立基於動力學的龍貝格觀測器,採用觀測器估計得到動力學質心側偏角估計值
(3)採用下述公式對和進行融合,得到質心側偏角估計值
其中,τ為濾波常數,s為拉氏算子。
步驟(1)具體包括:
(1a)實時測量車身側向加速度ay、縱向車速v和車身橫擺角速度即為車身橫擺角速度利用陀螺儀直接測量得到,ψ為車身橫擺角;
(2a)根據下述運動學估計公式求取
其中,β0為質心側偏角初始值。
步驟(1a)中還需實時測量方向盤轉角γ,為了解決積分法誤差積累的問題,步驟(2a)中,以方向盤轉角信號為依據,當方向盤轉角γ變化範圍在±10°以內保持5s以上,設置積分重置機制,以減小誤差積累。
步驟(2)中的線性二自由度單軌車輛模型為:
其中,cf1和cf2分別為前輪模型參數,cr1和cr2分別表示後輪模型參數,cf1、cf2、cr1和cr2均為常數,δ為前輪轉角,j為車身橫擺轉動慣量,lf和lr分別為車輛質心至前軸和後軸的距離,m為車輛質量,v為縱向車速,為車身橫擺角速度,β為動力學質心側偏角;
αf和αr分別為前輪和後輪側偏角,具體為:
對於線性二自由度單軌車輛模型,構建廣義龍貝格觀測器對β進行觀測得到觀測值,β觀測值即為動力學質心側偏角估計值
本發明的原理:
(1)考慮積分重置的運動學估計法估計
本研究建立二自由度單軌車輛模型,如圖2所示,假定車輛的縱向速度不變,只考察車輛的側向運動和橫擺運動。
基於車輛運動學關係可以得到:
其中β0表示質心側偏角初始值,v為縱向車速,ay為車身側向加速度,為車身橫擺角速度。將等式兩邊進行積分,可得到:
其中β0表示質心側偏角初始值。
為了解決積分法誤差積累的問題,設置積分重置機制,當車輛保持較長時間直線行駛時,對積分法進行重置,以減小誤差積累。以方向盤轉角信號為依據,當方向盤轉角在±10°以內保持5s以上,重置積分。
(2)基於動力學的龍貝格觀測器估計
採用如下的反正切函數來描述輪胎側偏角-側向力的非線性關係:
fy=c1atan(c2α),
式中,c1和c2為輪胎模型參數,fy和α分別為輪胎的側向力和側偏角。
車輛運動學方程可以轉化成如下形式:
將車輛運動方程轉化為如下的狀態空間形式:
對於非線性狀態函數和觀測函數,其廣義龍貝格觀測器結構框圖如圖3所示,狀態方程為:
上式中表示反饋係數矩陣。
定義估計誤差:
將該非線性系統線性化,其雅克比矩陣元素為:
通過局部線性化處理,估計誤差可表示為:
定義誤差矩陣:
則誤差方程的解為:
上式中t0表示初始時刻。只要誤差矩陣f恆為負,那麼在任意初始條件下,經過有限長的時間,估計誤差將收斂到零,即估計值將收斂到真實值。因此,需要設計反饋增益矩陣,保證誤差矩陣的所有特徵根恆為負。
在二自由度模型中,選取前輪轉角作為系統輸入變量,橫擺角速度作為觀測變量,可得誤差矩陣表達式為:
上式中l1和l2表示反饋係數中的兩個元素。
則誤差矩陣的特徵根為:
得到系統兩個特徵根:
由於λ1恆小於零,選擇合適的l2,使λ2也小於零,保證觀測器的兩個特徵根都小於零,從而能夠使狀態觀測器在原點處收斂。
