基於3D‑SUSAN算子的三維模型感興趣點提取方法與流程
2023-12-08 23:11:01
本發明涉及三維模型感興趣點提取,具體講的是關於一種基於3D-SUSAN角點算子的三維模型感興趣點提取方法。
背景技術:
近年來3D應用得到了廣泛的關注,在三維模型發展的過程中,感興趣點提取是很多3D應用技術的本質,例如,網格簡化、網格分割、視點選擇和三維模型匹配檢索。使用感興趣點匹配三維模型,需要提供模型的局部特徵點。這種方法也適用於三維圖片識別、匹配。
在感興趣點提取的領域中,無論是在理論上還是在實際3D應用中,我們都可以目睹這種技術的巨大進步。這些進步可以從模型分析、模型傳送和模型渲染上得以體現。感興趣點提取技術通常使用數學手段提取特徵,比如幾何數學中的曲率,曲率越大越顯著。
三維模型感興趣點提取也面臨著一些挑戰和困難。首先,到現在為止都不存在明確的關於感興趣點的定義。基於一些主觀研究表明感興趣點是指點與其他點存在較大的差異的點。然後,由於3D網格的拓撲方向是任意的,模型頂點就有任意的鄰居頂點。最後,除了頂點的位置信息,沒有其他有關頂點的信息,因此需要計算頂點的其他特徵信息。
二維角點檢測算子可以籠統地歸納為3類分別是基於灰度圖像的角點檢測、基於二值圖像的角點檢測和基於輪廓曲線的角點檢測。常見的角點算子包括Moravec角點檢測算子、Harris角點檢測算子和SUSAN角點檢測算子等。其中SUSAN角點檢測算子根據與每一圖像點相關的局部區域具有相同的像素值。如果某一窗口區域內的每一個像素值與該窗口中心的像素值相同或相似,我們將該區域稱之為USAN區域。若USAN區域小於閾值,我們將認為該區域的中心點為角點。
參考文獻
[1]HelinDutagaci,Chun Pan Cheung,AfzalGodil,「Evaluation of 3D interest point detection techniquesvia human-generated ground truth」,Springer-Verlag,2012.
[2]C.H.Lee,A.Varshney,and D.W.Jacobs,"Mesh Saliency,"ACM SIGGRAPH,vol.174,pp.659-666,2005.
[3]A Benchmark for 3D Interest Points Marked by Human Subjects,[Online].
Available:http://www.itl.nist.gov/iad/vug/sharp/benchmark/3DInterestPoint.
[4]Castellani,U.,Cristani,M.,Fantoni,S.,Murino,V.:Sparse pointsmatching by combining 3Dmesh saliency with statistical descriptors.Comput.Graph.Forum27(2),643–652(2008).
技術實現要素:
本發明的目的是鑑於三維模型感興趣點對網格簡化、網格分割、視點選擇和3D模型匹配檢索的重要性,提出一種基於3D-SUSAN角點算子的三維模型感興趣點提取方法,該方法將二維圖像特徵點提取的SUSAN角點檢測算子引入三維領域,提出了一種3D-SUSAN角點檢測算子,並有效提取三維模型感興趣點。該方法繼承了SUSAN算子的抗噪能力強、計算量小、效率高和性能穩定等特點。
為了實現上述目的,本發明通過以下技術方案予以實現,具體包括如下步驟::
步驟(1):利用網格讀取算法計算待提取三維模型的頂點位置坐標,並且利用網格簡化算子將待提取三維模型頂點進行簡化。
步驟(2):利用曲率算子計算每個頂點的曲率。
步驟(3):利用高斯函數對曲率值進行高斯處理,去除噪聲,得到去噪後的曲率值。
步驟(4):定義頂點集群,根據鄰居頂點與當前頂點的距離,選取距離最短的前36個鄰居頂點作為與當前頂點曲率值比較的頂點集群。
步驟(5):根據步驟(4)定義的頂點集群,若當前頂點與頂點集群內其他鄰居頂點的曲率差值小於定義的相似度閾值,則將該當前頂點作為候選點。然後比較候選點的USAN值與幾何閾值的大小,若USAN值小於幾何閾值大小,則將該候選點作為感興趣點返回。
步驟(6):定義評估算子FPE、FNE和WME[1],根據算法缺失率、多餘率、誤差率對步驟(5)得到的感興趣點進行評估。
步驟(2)所述的利用曲率算子計算每個頂點的曲率,其中曲率計算公式如下:
設三維曲線方程為:x=x(t),y=y(t),z=z(t);
1)分別求導,得到x′(t),y′(t),z′(t);
2)分別求2階導,得到x″(t),y″(t),z″(t);
3)將三個一階導合在一起看做一個三維矢量:
r′=(x′(t),y′(t),z′(t));
4)將三個二階導合在一起看做一個三維矢量:
r″=(x″(t),y″(t),z″(t));
5)曲率計算公式為:
所述的步驟(3)中利用高斯公式對步驟(2)中頂點曲率進行高斯函數處理,得到σ區域內平均曲率的高斯加權平均,所述的高斯函數公式如下:
G是σ區域內平均曲率的高斯加權平均,是頂點的曲率值,x是σ區域內當前計算頂點v的鄰居頂點。
步驟(4)中所述選取頂點集群是指以當前計算頂點為中心,選取距離最短的前36個鄰居頂點作為與當前頂點對比的頂點。
三維模型頂點距離計算公式為:
(x1,y1,z1),(x2,y2,z2)分別是兩個頂點的坐標。
所述步驟(5)的具體實現過程如下:
5-1.首先為了增加閾值自適應能力,需要動態計算每個中心頂點的所屬頂點集群內曲率差相似度閾值。
其中,中心頂點是指頂點集群中當前計算的頂點;a表示曲率差的平均值。c(v0)表示中心頂點曲率,c(v)表示頂點集群內其他鄰居頂點曲率。
t表示曲率相似度閾值,a表示曲率差的平均值,c表示集群內頂點的曲率值,N表示集群點個數,這裡取36。
若當前頂點與其鄰居頂點的曲率絕對值差值小於曲率相似度閾值,則將當前頂點作為候選點。
5-2.計算每個候選點的USAN值:
t表示曲率相似度閾值,c(v0)表示中心頂點曲率,c(v)表示頂點集群內其他鄰居頂點曲率。d表示某候選點的USAN值,其初始值為0。
參考應用在二維圖像焦點提取的SUSAN算子,一般在提取角點時幾何閾值等於USAN區域的1/2,因此在3D-SUSAN算子中,我們同樣選取USAN區域的1/2作為幾何閾值:
g(v0)表示v0的幾何閾值,d(v0)表示表示v0的USAN區域值。
若候選點的USAN值小於幾何閾值,則認為該候選點為角點。
5-3.對得到的角點做非極大值抑制,最終得到感興趣點。
步驟(6)所述的評估算法具體如下:評估算法具體分為兩步:一是建立模型真實場景,二是使用建立的真實場景評估感興趣點提取算法。
(1)建立模型真實場景興趣點標識的評估標準,該部分引用了網站A Benchmark for 3D Interest Points Marked by Human Subjects[2]的資料庫,包括三維模型以及每個模型的人工提取感興趣點坐標集。
(2)使用建立的真實場景評估興趣點提取算法,利用FPE(false positive errors)、FNE(false negative errors)和WME(weighted miss error)對算法提取的興趣點進行評估。
Gr=(p∈M|d(g,p)≤r)
Gr表示模型真實場景興趣點集,M表示算法提取模型的興趣點,d表示頂點與頂點的距離,r表示半徑的區域。
NC表示算法提取的正確的點數量,NG表示真實場景中總的興趣點個數。
NA表示算法提取的興趣點個數,NC表示算法提取得到的正確的點數量。
ni表示ni個志願者標識了i點,gi表示半徑為r時的真實場景3D-SUSAN評估結果。
本發明的有益效果如下:
本發明提出一種基於3D-SUSAN角點算子的三維模型感興趣點提取方法,該方法將用於二維圖像特徵點提取的SUSAN角點檢測算子引入三維領域,提出了一種3D-SUSAN角點檢測算子,並有效地提取三維模型的感興趣點。
3D-SUSAN角點檢測算子不僅可以提取三維模型興趣點而且仍保留了SUSAN的抗噪能力強、計算量小效率高、性能穩定的優點。
附圖說明
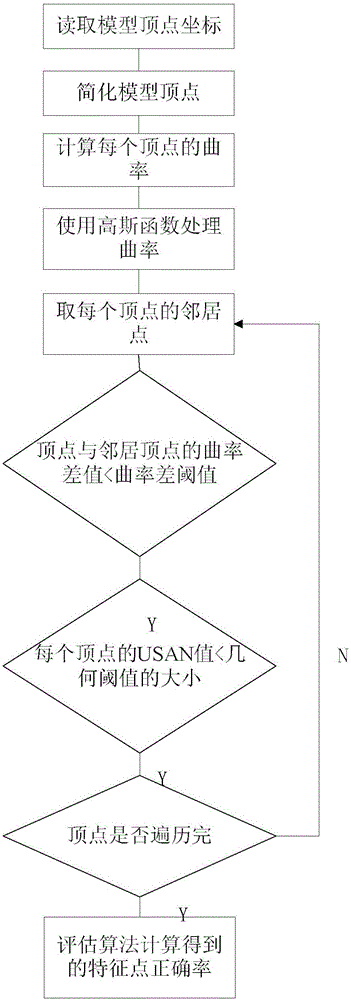
圖1是本發明基於3D-SUSAN算法的三維模型興趣點提取流程圖。
圖2是頂點集群圖。
圖3是非極大值抑制流程圖。
圖4是3D-SUSAN算法評估結果圖。
圖5是興趣點標識。
具體實施方式
下面結合附圖對本發明作進一步說明。
如圖1所示,一種基於3D-SUSAN角點算子的三維模型感興趣點提取方法,具體包括如下步驟:
步驟(1):利用網格讀取算法計算待提取三維模型的頂點位置坐標,並且利用網格簡化算子將待提取三維模型頂點進行簡化。
步驟(2):利用曲率算子計算每個頂點的曲率。
步驟(3):利用高斯函數對曲率值進行高斯處理,去除噪聲,得到去噪後的曲率值。
步驟(4):定義頂點集群,根據鄰居頂點與當前頂點的距離,選取距離最短的前36個鄰居頂點作為與當前頂點曲率值比較的頂點集群,附圖2是頂點集群圖。
步驟(5):根據步驟(4)定義的頂點集群,若當前頂點與頂點集群內其他鄰居頂點的曲率差值小於定義的相似度閾值,則將該當前頂點作為候選點。然後比較候選點的USAN值與幾何閾值的大小,若USAN值小於幾何閾值大小,則將該候選點作為感興趣點返回。
步驟(6):定義評估算子FPE、FNE和WME[1],根據算法缺失率、多餘率、誤差率對步驟(5)得到的感興趣點進行評估。
步驟(2)所述的利用曲率算子計算每個頂點的曲率,其中曲率計算公式如下:
設三維曲線方程為:x=x(t),y=y(t),z=z(t);
6)分別求導,得到x′(t),y′(t),z′(t);
7)分別求2階導,得到x″(t),y″(t),z″(t);
8)將三個一階導合在一起看做一個三維矢量:
r′=(x′(t),y′(t),z′(t));
9)將三個二階導合在一起看做一個三維矢量:
r″=(x″(t),y″(t),z″(t));
10)曲率計算公式為:
所述的步驟(3)中利用高斯公式對步驟(2)中頂點曲率進行高斯函數處理,得到σ區域內平均曲率的高斯加權平均,所述的高斯函數公式如下:
G是σ區域內平均曲率的高斯加權平均,是頂點的曲率值,x是σ區域內當前計算頂點v的鄰居頂點。
步驟(4)中所述選取頂點集群是指以當前計算頂點為中心,選取距離最短的前36個鄰居頂點作為與當前頂點對比的頂點。
三維模型頂點距離計算公式為:
(x1,y1,z1),(x2,y2,z2)分別是兩個頂點的坐標。
所述步驟(5)的具體實現過程如下:
5-1.首先為了增加閾值自適應能力,需要動態計算每個中心頂點的所屬頂點集群內曲率差相似度閾值。
其中,中心頂點是指頂點集群中當前計算的頂點;a表示曲率差的平均值。c(v0)表示中心頂點曲率,c(v)表示頂點集群內其他鄰居頂點曲率。
t表示曲率相似度閾值,a表示曲率差的平均值,c表示集群內頂點的曲率值,N表示集群點個數,這裡取36。
若當前頂點與其鄰居頂點的曲率絕對值差值小於曲率相似度閾值,則將當前頂點作為候選點。
5-2.計算每個候選點的USAN值:
t表示曲率相似度閾值,c(v0)表示中心頂點曲率,c(v)表示頂點集群內其他鄰居頂點曲率。d表示某候選點的USAN值,其初始值為0。
參考應用在二維圖像焦點提取的SUSAN算子,一般在提取角點時幾何閾值等於USAN區域的1/2,因此在3D-SUSAN算子中,我們同樣選取USAN區域的1/2作為幾何閾值:
g(v0)表示v0的幾何閾值,d(v0)表示表示v0的USAN區域值。
若候選點的USAN值小於幾何閾值,則認為該候選點為角點。
5-3.對得到的角點做非極大值抑制,最終得到感興趣點,附圖3是非極大值抑制流程圖。
步驟(6)所述的評估算法具體如下:評估算法具體分為兩步:一是建立模型真實場景,二是使用建立的真實場景評估感興趣點提取算法。
(1)建立模型真實場景興趣點標識的評估標準,該部分引用了網站A Benchmark for 3D Interest Points Marked by Human Subjects[2]的資料庫,包括三維模型以及每個模型的人工提取感興趣點坐標集。
(2)使用建立的真實場景評估興趣點提取算法,利用FPE(false positive errors)、FNE(false negative errors)和WME(weighted miss error)對算法提取的興趣點進行評估。
Gr=(p∈M|d(g,p)≤r)
Gr表示模型真實場景興趣點集,M表示算法提取模型的興趣點,d表示頂點與頂點的距離,r表示半徑的區域。
NC表示算法提取的正確的點數量,NG表示真實場景中總的興趣點個數。
NA表示算法提取的興趣點個數,NC表示算法提取得到的正確的點數量。
ni表示ni個志願者標識了i點,gi表示半徑為r時的真實場景3D-SUSAN評估結果見附圖43D-SUSAN算法評估結果圖。
FNE表示缺失率、FPE表示多餘率、WME表示誤差率,當它們降低速率越快,證明該算法提取興趣點結果越好。
本發明針對算法提取三維模型興趣點的結果,從錯誤率、缺失率、誤差率進行評估,並與Meshsaliency提取的興趣點作比較。從附圖5中就可以看出,與Mesh saliency[3]相比,3D-SUSAN提取的興趣點明顯比Mesh saliency提取的興趣點少,而從附圖5可以看出,3D-SUSAN的標識結果和人類標識的興趣點差不多一樣。由此可以得出該發明在減少算法提取三維模型興趣點數量上有所提高。
