一種基於自制地基雷射雷達鉛垂度誤差的點雲誤差校正方法與流程

2023-05-16 19:37:31

本發明涉及雷射雷達測量技術領域，尤其是一種基於自制地基雷射雷達鉛垂度誤差的點雲誤差校正方法

背景技術：

雷射雷達測量技術是近些年來快速發展的一種新興主動遙感技術，一般採用非接觸式測量技術，在遙感、軍事探測、海洋測繪、大氣勘探領域有著廣泛的應用。雷射雷達中的三維掃描測量技術在傳統單點測量技術的基礎上，通過高速雷射掃描的方式，可以快速獲取目標物體表面的高解析度點雲數據，該項技術具有數據處理簡單、快速性、主動性、抗幹擾能力強、測量精度高、範圍大等優點。但雷射雷達掃描精度很大程度上受到自身儀器精度影響，實際使用中，儀器的精度本身不完全符合其標稱精度，或者因使用時的外力碰撞、外界條件變化、長時間使用帶來的損耗以及其他未知因素造成儀器性能不穩定，掃描結果可能出現系統性誤差。因此，有效消除雷射雷達儀器誤差，是提高掃描點雲精度的關鍵。

根據現有研究成果，雷射雷達主要分為機載雷射雷達和地面雷射雷達兩大類，關於雷射雷達三維成像系統的點雲誤差校正方法也各有不同，第一類基於機載雷射雷達系統的標定方法以飛行自標定為主，基本思想是利用雷射對已知的目標點或者相對目標點進行掃描，對過程中產生的固定偏移量進行參數估計，包括重疊航帶標定技術、最小二乘平差法幾何標定技術等。其中，重疊航帶標定技術對航帶拼接技術有著較高的要求；平差法求解中的假設前提條件一般難以成立，可能造成參數估計精度下降等問題。上述機載雷射雷達系統的標定方法和本發明無對比，無借鑑。

第二類基於地面雷射雷達系統的標定方法絕大多數是在室內或者基線場完成，一些涉及點位精度的檢定實驗主要採用公共點轉換的方法，大多採用系統配套的標靶進行試驗，包括空間長度檢測法、自檢校法等。空間長度檢測法對檢測場有著較高要求，需要場地具有很高精度，較依賴掃描目標布設的精度；自檢校法一般採用全站儀、經緯儀等儀器對雷射雷達系統建立檢校模型，模型一般包含坐標系旋轉角、平移量以及儀器內部誤差等參數，將這些參數作為未知量經過統一求解得出來，該方法可以通過增加參數的方式不斷完善誤差模型，提高系統誤差的校正精度，檢校雷射雷達系統的範圍比較廣泛，且對目標物體的布設精度沒有十分高的要求。本發明就屬於一種系統自檢校方法。

根據現有專利局提供的專利查閱，地面雷射雷達系統的自檢校方法主要分為以下兩類：第一類方法採用公共標誌點得到待校準系統與高精度掃描儀之間的坐標旋轉、平移量，直接以待校準系統測量值與標準測量值之差作為系統空間坐標測量誤差。該類方法針對所有空間三維坐標測量系統，得到空間坐標測量相對誤差，其缺點是僅在三維點雲層面評估和校正誤差，未構建系統誤差模型，且需要大量樣本數據才能實現精確校正；上述專利包括在中國專利200810147441.9中公開的「一種電子經緯儀空間坐標測量系統的校準方法」。第二類方法採用統計學方法對系統測距誤差和測角誤差的概率密度分布進行分析，得到三維坐標系中的誤差修正樣本。該類方法針對所有三維坐標測量系統，得到系統誤差修正模型，其缺點是系統誤差模型參數沒有物理意義，並未針對系統本身掃描方式從誤差源的角度進行理論分析，因此依賴大樣本數據才能實現精確校正；上述專利包括在中國專利201710014687.8中公開的「一種遠距離掃描雷射雷達測量誤差的修正方法」。

本發明與現有系統自檢校方法專利的主要區別在於：提出了一種針對系統本身掃描方式從誤差源的角度進行理論分析、利用少量目標點實現自制地基雷射雷達鉛垂度誤差點雲誤差校正的方法，適用於所有採用45°轉鏡配合雲臺轉動掃描方式的三維掃描系統。本發明在雷射雷達測量技術領域具有廣闊的應用前景。

技術實現要素：

本發明公開一種基於自制地基雷射雷達鉛垂度誤差的點雲誤差校正方法，其特徵在於，該方法針對自製雷射雷達三維成像系統中45°轉鏡配合雲臺轉動的掃描方式，其中所述自製雷射雷達三維成像系統包括光學系統、掃描機構(電機、45°轉鏡)、雲臺；入射光經所述光學系統出射到所述45°轉鏡中心(o點)，伴隨所述掃描機構垂直旋轉、所述雲臺水平旋轉從所述自製雷射雷達三維成像系統中出射；所述自製雷射雷達三維成像系統的理想坐標系(o-xyz)包括俯仰軸(x軸)、初始出射光線方向(y軸)和方位軸(z軸)；所述自製雷射雷達三維成像系統的實際坐標系(o-x』y』z』)在所述理想坐標系(o-xyz)基礎上，實際方位軸(z』軸)與所述z軸之間存在夾角α，即所述實際方位軸(z』軸)不鉛垂，且所述實際方位軸(z』軸)在xoy平面上的投影與所述x軸之間存在夾角θ，由於實際俯仰軸與所述實際方位軸互相垂直，因此x』軸為所述實際俯仰軸，根據右手坐標法則建立y』軸；所述鉛垂度誤差定義為：①所述實際方位軸(z』軸)與所述z軸之間的夾角α；②所述實際方位軸(z』軸)在所述xoy平面上的投影與所述x軸之間的夾角θ，從x軸正半軸起算，逆時針方向為正，範圍為0°至360°；目標上一點p在所述理想坐標系(o-xyz)中一維距離l定義為的長度，方位角定義為在所述xoy平面的投影與x軸的夾角，從x軸正半軸起算，逆時針方向為正，範圍為0°至360°，俯仰角定義為90°與和z軸之間夾角的差，所述一維距離l、所述方位角和所述俯仰角的測量誤差分別為測距誤差δl、方位角誤差和俯仰角誤差通過理論分析所述鉛垂度誤差(α、θ)對所述自製雷射雷達三維成像系統測角誤差(方位角誤差俯仰角誤差)的影響，建立所述自製雷射雷達三維成像系統的測角誤差模型；所述目標的點雲定義為目標上一點的直角坐標(x,y,z)t，目標的點雲誤差定義為所述目標點雲的坐標測量值與真實值的偏差(δx,δy,δz)t，根據所述目標的點雲誤差(δx,δy,δz)t與所述目標測角誤差(方位角誤差俯仰角誤差)之間的誤差傳遞原則，建立所述自製雷射雷達三維成像系統的點雲誤差模型如下：

得到所述自製雷射雷達三維成像系統對所述鉛垂度誤差(α、θ)校正後的所述目標點雲坐標為：

(x+δx,y+δy,z+δz)t

從而實現對所述自製雷射雷達三維成像系統鉛垂度誤差(α、θ)的點雲誤差校正；

所述方法主要包括以下七步：

1)建立所述自製雷射雷達三維成像系統理想坐標系(o-xyz)，由於實際方位軸(z』軸)不鉛垂，即所述實際方位軸(z』軸)與所述理想方位軸(z軸)之間存在夾角α，所述實際方位軸(z』軸)在所述xoy平面上的投影與所述理想俯仰軸(x軸)之間存在夾角θ，從x軸正半軸起算，逆時針方向為正，範圍為0°至360°，且所述實際俯仰軸與所述實際方位軸(z』軸)互相垂直，因此x』軸定義為所述實際俯仰軸，根據右手坐標法則建立y』軸，為所述自製雷射雷達三維成像系統實際坐標系(o-x』y』z』)；所述目標上任意一點p在所述理想坐標系(o-xyz)中的測量值為方位角俯仰角所述目標上任意一點p在所述理想坐標系(o-xyz)中的真實值為方位角俯仰角所述和差值為方位角誤差所述和差值為俯仰角誤差

2)建立由所述鉛垂度誤差(α、θ)引起的所述自製雷射雷達三維成像系統測角誤差模型；該模型分別描述了所述測角誤差(方位角誤差俯仰角誤差)和所述鉛垂度誤差(α、θ)以及所述目標的方位角俯仰角之間的數學關係，如下所示：

3)基於對所述鉛垂度誤差(α、θ)的三角函數值進行近似變換，化簡所述自製雷射雷達三維成像系統測角誤差模型，如下所示：

4)根據誤差傳遞原則，建立所述自製雷射雷達三維成像系統的點雲誤差(δx,δy,δz)t與所述測距誤差δl、所述測角誤差(方位角誤差俯仰角誤差)之間的映射關係，如下所示：

其中，l為所述目標上任意一點在所述自製雷射雷達三維成像系統理想坐標系(o-xyz)中的一維距離，δl為所述目標上任意一點一維距離l的測量誤差；

5)將所述自製雷射雷達三維成像系統測角誤差模型轉化到直角坐標系下，得到所述自製雷射雷達三維成像系統的點雲誤差模型如下：

6)利用所述自製雷射雷達三維成像系統對n個所述目標進行掃描，得到所述目標在所述自製雷射雷達三維成像系統中的坐標(xi,yi,zi)t，(i＝1,2,…,n)，作為測量值；利用高精度三維掃描儀對所述目標進行二次掃描，得到所述目標在所述高精度三維掃描儀中的坐標(x′i,y′i,z′i)t，(i＝1,2,…,n)，將其轉化到所述自製雷射雷達三維成像系統下，作為真實值；所述測量值與所述真實值之差為所述自製雷射雷達三維成像系統的點雲誤差(δxi,δyi,δzi)t，(i＝1,2,…,n)；根據球坐標系與直角坐標系之間的映射關係，由所述測量值得到所述目標的一維距離li、方位角和俯仰角所述目標的測距誤差δli在所述一維距離li處於一定範圍內時視為一個已知常數；

7)求解所述自製雷射雷達三維成像系統點雲誤差模型中的模型參數，即所述鉛垂度誤差(α、θ)，對所述自製雷射雷達三維成像系統鉛垂度誤差(α、θ)的點雲誤差進行校正；將所述自製雷射雷達三維成像系統的點雲誤差(δxi,δyi,δzi)t，(i＝1,2,…,n)、所述目標的一維距離li、方位角俯仰角和測距誤差δli代入所述公式(4)中，得到3*n個非線性方程，通過求解所述非線性方程確定所述自製雷射雷達三維成像系統點雲誤差模型中的所述鉛垂度誤差(α、θ)；將所述鉛垂度誤差(α、θ)代入式(4)，在所述自製雷射雷達三維成像系統的所述目標點雲坐標(x,y,z)t基礎上，得到所述自製雷射雷達三維成像系統校正後的所述目標點雲坐標(x+δx,y+δy,z+δz)t。

其中，建立所述自製雷射雷達三維成像系統理想坐標系(o-xyz)；所述自製雷射雷達三維成像系統的俯仰軸定義為所述45°轉鏡的電機轉軸，方位軸定義為所述雲臺的轉軸；理想情況下，所述方位軸與鉛垂軸重合；所述45°轉鏡的反射面中心，即所述入射光入射到所述反射面上的交點為坐標原點o；與所述俯仰軸重合，正方向與所述入射光入射到所述45°轉鏡上的方向相同的坐標軸定義為x軸；與所述入射光初始出射方向相同的坐標軸定義為y軸；與所述方位軸重合，正方向豎直向上的坐標軸定義為z軸。

其中，建立由所述鉛垂度誤差(α、θ)引起的所述自製雷射雷達三維成像系統測角誤差模型並化簡；由於所述實際方位軸(z』軸)不鉛垂，即所述實際方位軸(z』軸)與所述理想方位軸(z軸)之間存在夾角α，所述實際方位軸(z』軸)在所述xoy平面上的投影與所述理想俯仰軸(x軸)之間存在夾角θ，從x軸正半軸起算，逆時針方向為正，範圍為0°至360°；所述自製雷射雷達三維成像系統測角誤差模型的建立過程如下：

初始所述45°轉鏡法線單位矢量(所述o-x』y』z』坐標系下)為：

理想情況下出射光線經過所述目標上一點p，此時所述45°轉鏡法線矢量(所述o-x』y』z』坐標系下)為：

式(6)中為所述目標上一點p的所述俯仰角測量值，為所述目標上一點p的所述方位角測量值，分別為繞所述x』軸逆時針旋轉所述角、繞所述z』軸逆時針旋轉所述角的旋轉矩陣，所述旋轉矩陣如下：

將式(5)和式(7)代入式(6)，可得所述o-x』y』z』坐標系下所述45°轉鏡的法線矢量如下：

在o-x』y』z』坐標系下，初始所述入射光矢量為經所述雲臺轉動後變為由光反射定律的矢量形式為求得出射光矢量為

將所述出射光矢量轉換到o-xyz坐標系下為根據球坐標與直角坐標之間的轉換關係，如下式(9)，可求得所述方位角與所述俯仰角的真實值

根據三角函數近似原則，所述方位角誤差與所述俯仰角誤差可以近似成如下形式：

得到的所述自製雷射雷達三維成像系統測角誤差模型包括所述方位角誤差與俯仰角誤差描述了所述測角誤差(方位角誤差俯仰角誤差)和所述鉛垂度誤差(α、θ)以及所述方位角所述俯仰角之間的數學關係；

根據三角函數近似原則sinα＝α，cosα＝1，併合理省略部分α的高次項，得到化簡後所述自製雷射雷達三維成像系統測角誤差模型如下：

其中，所述自製雷射雷達三維成像系統球坐標系中的測角誤差模型轉換至所述自製雷射雷達三維成像系統直角坐標系中的點雲誤差模型；所述自製雷射雷達三維成像系統掃描後可以直接得到所述目標上一點p的所述一維距離l、所述方位角與所述俯仰角的測量值，根據式(9)轉換至所述自製雷射雷達三維成像系統直角坐標系下得到所述目標上一點p的空間三維坐標(x,y,z)t；

由於存在所述測距誤差δl和所述測角誤差(方位角誤差俯仰角誤差)，所述目標上一點p的坐標測量值為p'(x+δx,y+δy,z+δz)，其中(δx,δy,δz)t為所述目標的點雲誤差，根據誤差傳遞公式，得所述自製雷射雷達三維成像系統點雲誤差模型如下：

其中，所述目標在所述高精度三維掃描儀中的坐標轉換至所述自製雷射雷達三維成像系統中；所述自製雷射雷達三維成像系統點雲誤差模型中的所述鉛垂度誤差(α、θ)未知且不易測量，因此利用所述自製雷射雷達三維成像系統與所述高精度三維掃描儀中的點雲坐標數據求解所述鉛垂度誤差(α、θ)實現點雲誤差校正；利用所述自製雷射雷達三維成像系統對n個所述目標進行掃描，得到全部所述目標上一點在所述自製雷射雷達三維成像系統坐標系下的坐標(xi,yi,zi)t,(i＝1,2,…,n)，作為測量值；將所述測量值代入式(9)，得到全部所述目標的一維距離li、俯仰角和方位角利用所述高精度三維掃描儀對相同所述目標進行掃描，得到所述目標上一點在所述高精度三維掃描儀坐標系下的坐標(x′i,y′i,z′i)t,(i＝1,2,…,n)；由於所述(xi,yi,zi)t與所述(x′i,y′i,z′i)t處於不同的坐標系下，因此將所述(x′i,y′i,z′i)t轉換至所述自製雷射雷達三維成像系統坐標系下，作為真實值；所述高精度三維掃描儀到所述自製雷射雷達三維成像系統的旋轉矩陣r和平移矢量t表示如下：

式(13)與(14)中a、b、c分別是繞所述高精度三維掃描儀坐標系各軸逆時針旋轉的角度，x0、y0、z0分別是所述x、y、z三個方向上的位移，所述(x′i,y′i,z′i)t在所述自製雷射雷達三維成像系統中的坐標如下：

其中，求解所述自製雷射雷達三維成像系統點雲誤差模型中的模型參數，即所述鉛垂度誤差(α、θ)；所述自製雷射雷達三維成像系統點雲誤差模型可寫作如下形式：

所述測距誤差δli主要受所述自製雷射雷達三維成像系統中測距電路影響，在所述一維距離li處於一定範圍內時為一個已知常數；將所述(xi,yi,zi)t、所述(x′i,y′i,z′i)t、所述一維距離li、所述方位角和所述俯仰角代入式(15)與式(16)，基於最小二乘法求解3*n個非線性方程，可以確定所述旋轉矩陣r和所述平移矢量t(a，b，c,x0,y0,z0)與所述鉛垂度誤差(α、θ)共8個未知量。

其中，利用求解所得的所述鉛垂度誤差(α、θ)完善所述自製雷射雷達三維成像系統的點雲誤差模型，實現對所述自製雷射雷達三維成像系統鉛垂度誤差的點雲誤差校正；將所述鉛垂度誤差(α、θ)代入式(11)和式(12)，得到所述自製雷射雷達三維成像系統的點雲誤差(δx,δy,δz)t，在所述自製雷射雷達三維成像系統的所述目標點雲坐標(x,y,z)t基礎上，得到所述自製雷射雷達三維成像系統對所述鉛垂度誤差(α、θ)校正後的所述目標點雲坐標(x+δx,y+δy,z+δz)t。

其中，用於所述自製雷射雷達三維成像系統鉛垂度誤差點雲誤差校正的所述目標包含但不限於標靶球、平面反光標靶等所有可獲得所述目標上一點空間坐標的物體。

附圖說明

圖1是自製雷射雷達三維成像系統對目標掃描的空間示意圖；

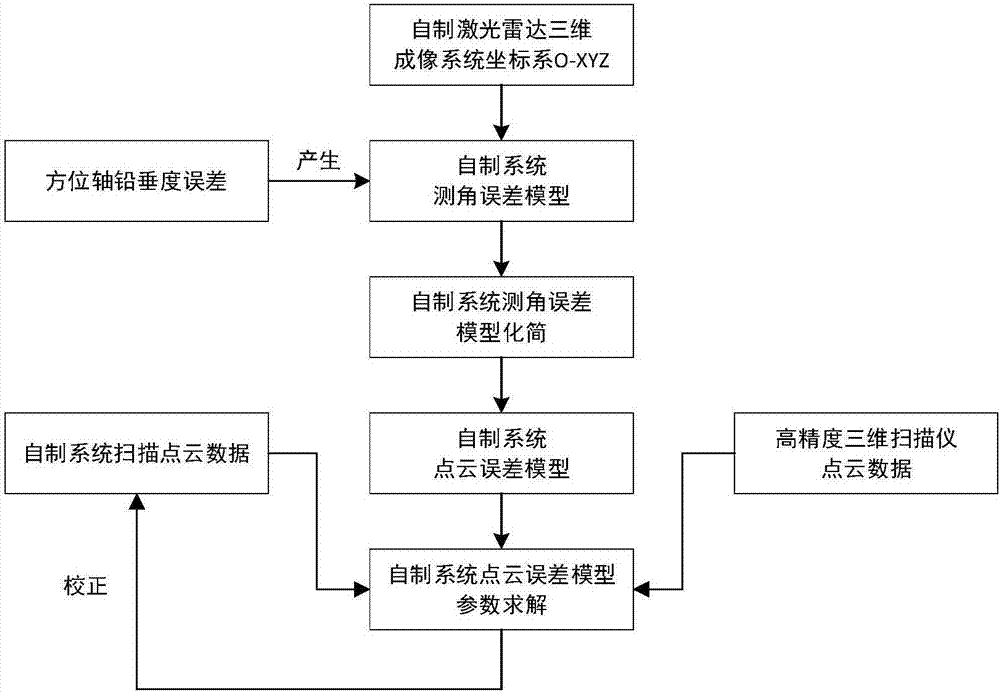
圖2是自制地基雷射雷達鉛垂度誤差的點雲誤差校正流程示意圖；

圖3是自製系統坐標系下方位軸的鉛垂度誤差示意圖；

圖4是自製系統全量程掃描過程中測角誤差變化的仿真結果；

圖5是自製系統測角誤差模型化簡前後測角誤差仿真的對比結果；

圖6是自製系統點雲誤差模型中參數確立的流程示意圖；

圖7是自製系統點雲誤差模型中參數確立的掃描方案示意圖；

具體實施方式

以下結合附圖對本發明專利的具體實施方式作進一步詳細描述。基於自制地基雷射雷達鉛垂度誤差的點雲誤差校正方法流程示意圖如圖2所示，先建立自製雷射雷達三維成像系統(713)理想坐標系o-xyz，由於實際情況下自製系統中實際方位軸z』軸(206)存在鉛垂度誤差(α、θ)(301、302)，在自製雷射雷達三維成像系統(713)坐標系下理論推導出鉛垂度誤差(α、θ)(301、302)對於自製雷射雷達三維成像系統(713)測角誤差的影響，得到自製雷射雷達三維成像系統(713)測角誤差模型。根據三角函數近似原則，對自製雷射雷達三維成像系統(713)測角誤差模型進行化簡。根據誤差傳遞原則，將自製雷射雷達三維成像系統(713)測角誤差模型轉化到直角坐標系下，得到自製雷射雷達三維成像系統(713)點雲誤差模型。利用自製雷射雷達三維成像系統(713)與高精度三維掃描儀(714)對相同標靶球(701-712)進行掃描，分別得到兩組目標點雲數據，在實現坐標系統一後將數據代入自製雷射雷達三維成像系統(713)點雲誤差(說明書表達式(15)與(16))中，求解模型參數，即鉛垂度誤差(α、θ)(301、302)，並利用此結果實現自製雷射雷達三維成像系統(713)點雲的誤差校正。故具體的實施方案可以分為四步：自製雷射雷達三維成像系統測角誤差模型的建立、自製雷射雷達三維成像系統測角誤差模型的化簡、自製雷射雷達三維成像系統點雲誤差模型的建立和模型的參數求解與校正。

(1)自製雷射雷達三維成像系統測角誤差模型的建立

自製雷射雷達三維成像系統(713)對目標(106)掃描的空間示意圖如圖1所示，自製雷射雷達三維成像系統(713)進行掃描時，入射光(105)經過光學系統(101)後入射至45°轉鏡(103)中心o點，該點作為坐標原點。電機(102)控制45°轉鏡(103)垂直旋轉，電機(102)轉軸即為俯仰軸，與x軸(201)重合，x軸(201)正方向與入射光(105)入射方向相同。同時雲臺(104)繞鉛垂軸水平旋轉，z軸(203)與鉛垂軸重合，且正方向豎直向上。建立右手坐標系，認為初始雷射出射方向為y軸(202)正方向，實現對三維空間的掃描。

自製雷射雷達三維成像系統(713)坐標系下方位軸鉛垂度誤差(301、302)存在的示意圖如圖1和圖3所示，實際情況下實際方位軸(z』軸)(206)與z軸(203)之間存在夾角α(301)，即所述實際方位軸(z』軸)(206)不鉛垂，且所述實際方位軸(z』軸)(206)在xoy平面上的投影與所述x軸(201)之間存在夾角θ(302)，從x軸正半軸起算，逆時針方向為正，範圍為0°至360°，建立了自製雷射雷達三維成像系統(713)的實際坐標系o-x』y』z』。目標物體(106)是一個標靶球，標靶球上任意一點為p點(107)，認為出射光線在空間中經過p點(107)，此時出射雷射的方位角(303)和俯仰角(304)分別測量為和o-x』y』z』坐標系下45°轉鏡(103)的法線矢量如下：

o-x』y』z』坐標系下入射光(105)矢量為由反射定律的矢量形式可以得到出射光矢量

將出射光矢量轉換到o-xyz坐標系下為根據球坐標與直角坐標之間的轉換關係，如式(9)，可求得方位角(303)與俯仰角(304)的真實值根據三角函數近似原則，方位角誤差與俯仰角誤差可以近似成如下形式：

最終建立的自製雷射雷達三維成像系統(713)測角誤差模型包括方位角誤差與俯仰角誤差誤差模型結果如下：

因此自製雷射雷達三維成像系統(713)測角誤差(方位角誤差俯仰角誤差)受鉛垂度誤差(α、θ)(301、302)以及方位角(303)、俯仰角(304)影響。假設自製雷射雷達三維成像系統(713)鉛垂度誤差(301、302)參量為α＝5"，θ＝80°，垂直掃描範圍為水平掃描範圍為自製雷射雷達三維成像系統(713)全量程掃描過程中測角誤差(方位角誤差俯仰角誤差)變化的仿真結果如圖4所示。結果表明：方位角誤差在水平與垂直掃描過程中均發生變化，在或2π、(303、304)處取得最大值，數量級為10-1；俯仰角誤差在垂直掃描過程中不變，在水平掃描過程中近似呈正弦變化，在或(303)處取得最大值，數量級為10-5。該仿真結果可以直觀地顯示自製雷射雷達三維成像系統(713)中存在一定鉛垂度誤差(α、θ)(301、302)時，整個掃描過程中測角誤差的變化情況。

(2)自製雷射雷達三維成像系統測角誤差模型的化簡

上述自製雷射雷達三維成像系統(713)測角誤差模型較為複雜，需要進行合理簡化。根據三角函數近似原則sinα＝α，cosα＝1，並且合理省略部分α的高次項，得到化簡後的自製雷射雷達三維成像系統(713)測角誤差模型如下：

假設鉛垂度誤差(301、302)參量為α＝5"，θ＝80°，垂直掃描範圍為水平掃描範圍為比較化簡前後的模型，自製雷射雷達三維成像系統(713)測角誤差模型化簡前後仿真的對比結果如圖5所示。結果表明：化簡前後方位角誤差與俯仰角誤差隨掃描過程測量值變化相同，模型化簡過程正確，將化簡後的模型作為自製雷射雷達三維成像系統(713)的測角誤差模型。

(3)自製雷射雷達三維成像系統點雲誤差模型的建立

自製雷射雷達三維成像系統(713)最終得到並顯示的是目標標靶球(106)的點雲數據，數據格式為直角坐標系下目標點(107)空間三維坐標(x,y,z)t(306)，坐標轉換的關係如式(9)，其中l是目標點的一維距離(305)的測量值，是目標方位角(303)的測量值，是俯仰角(304)的測量值。

由誤差傳遞公式，得到自製雷射雷達三維成像系統(713)點雲誤差模型如下：

其中δx、δy、δz分別為x、y、z軸(201-203)坐標分量誤差值，δl為系統測距誤差，在一定測距範圍內可視為定值，為系統方位角誤差，為系統俯仰角誤差，可由上述自製雷射雷達三維成像系統(713)測角誤差模型表示。

(4)模型的參數求解與校正

自製雷射雷達三維成像系統(713)點雲誤差模型中參數確立的流程示意圖如圖6所示，取n個標靶球(701-712)作為目標，分別用自製雷射雷達三維成像系統(713)與高精度三維掃描儀(714)對其進行掃描，可得到每個標靶球(701-712)上多點的點雲數據，利用最小二乘法對每個標靶球(701-712)上點雲進行空間擬合，分別得到自製雷射雷達三維成像系統(713)下的球心坐標(xi,yi,zi)t,(i＝1,2,…,n)和高精度三維掃描儀(714)下的球心坐標(x′i,y′i,z′i)t,(i＝1,2,…,n)。將(x′i,y′i,z′i)t,(i＝1,2,…,n)進行旋轉和平移轉化到自製雷射雷達三維成像系統(713)坐標系下，一起代入自製雷射雷達三維成像系統(713)點雲誤差表達式(15)和式(16)中，採用最小二乘法對模型參數進行求解，用得到鉛垂度誤差(α、θ)(301、302)實現自製雷射雷達三維成像系統(713)的點雲誤差校正。具體的掃描方案如下：

自製雷射雷達三維成像系統(713)點雲誤差模型中參數確立的掃描方案示意圖如圖7所示，取n＝12，即準備標靶球12個(701-712)，在室內空曠場地內任意布設，將自製雷射雷達三維成像系統(713)置於中心處，使標靶球(701-712)遍布自製雷射雷達三維成像系統(713)水平掃描範圍，高低遍布自製雷射雷達三維成像系統(713)垂直掃描範圍內，每個標靶球(701-712)與自製雷射雷達三維成像系統(713)距離大致相同，此時測距誤差為一個已知的常數。利用自製雷射雷達三維成像系統(713)對所有標靶球(701-712)進行掃描，經過球心擬合後得到全部標靶球(701-712)球心坐標(xi,yi,zi)t,(i＝1,2,…,12)，作為測量值，並求得每個標靶球(701-712)球心的一維距離li(305)、俯仰角(304)和方位角(303)。利用高精度三維掃描儀(714)進行二次掃描，得到所有標靶球(701-712)球心坐標(x′i,y′i,z′i)t,(i＝1,2,…,12)，通過旋轉和平移將其轉化到自製雷射雷達三維成像系統(713)坐標系下，作為真實值，旋轉矩陣r和平移矢量t如下：

式中a、b、c分別是繞高精度三維掃描儀(714)坐標系各軸逆時針旋轉的角度，x0、y0、z0分別是x、y、z(201-203)三個方向上的位移，自製雷射雷達三維成像系統(713)點雲誤差模型可寫作如下形式：

上述模型中有a,b,c,x0,y0,z0,α,θ共8個未知參數，將其中4個標靶球(701、704、707、710)的球心坐標代入式(19)，可得到12個非線性方程。首先假設不存在鉛垂度誤差(α、θ)(301、302)，即式(19)等號右側為0，代入標靶球(701、704、707、710)球心坐標數據，採用最小二乘法解非線性方程組可以求得a,b,c,x0,y0,z0的初始值，默認鉛垂度誤差(α、θ)(301、302)初始值為0。初始值確定後，採用最小二乘法求解8個未知參數，將鉛垂度誤差(α、θ)(301、302)代入式(11)和式(12)，得到系統點雲誤差(δx,δy,δz)t，利用剩餘8個標靶球(702、703、705、706、708、709、711和712)球心的坐標數據對模型進行檢驗，不斷修正模型，最終得到的模型可以實現自製雷射雷達三維成像系統(713)鉛垂度誤差(α、θ)(301、302)的點雲誤差校正，校正後的目標點雲坐標為(x+δx,y+δy,z+δz)t。

綜上所述，本發明提出一種基於自制地基雷射雷達鉛垂度誤差的點雲誤差校正方法，該方法主要針對自製雷射雷達三維成像系統45°轉鏡配合雲臺轉動的掃描方式，通過計算方位軸鉛垂度誤差對自製雷射雷達三維成像系統測角誤差的影響，建立自製雷射雷達三維成像系統點雲誤差模型，並採用高精度三維掃描儀的點雲坐標作為真實值求解鉛垂度誤差，從而實現對自製雷射雷達三維成像系統鉛垂度誤差目標點雲的誤差校正。本發明是一種從自製雷射雷達三維成像系統誤差源出發的、利用少量目標點即可實現的、理論性與邏輯性較強的系統點雲誤差校正方法，該方法適用於所有採用45°轉鏡配合雲臺轉動掃描方式的三維掃描系統。

以上所述，僅為本發明具體實施方法的基本方案，但本發明的保護範圍並不局限於此，任何熟悉本技術領域的人員在本發明公開的技術範圍內，可想到的變化或替換，都應涵蓋在本發明的保護範圍之內。因此，本發明的保護範圍應該以權利要求的保護範圍為準。所有落入權利要求的等同的含義和範圍內的變化都將包括在權利要求的範圍之內。