一種信道狀態不確定條件下分層異構網絡的穩健分層博弈學習資源分配方法與流程
2023-11-09 23:50:53
本發明涉及5G分層異構網絡的資源分配問題解決方案。該發明針對異構無線網絡在信道信息不完美條件下的幹擾管理問題,提出了一種基於魯棒雙層博弈的離散策略資源分配方案。屬於無線通信
技術領域:
。二
背景技術:
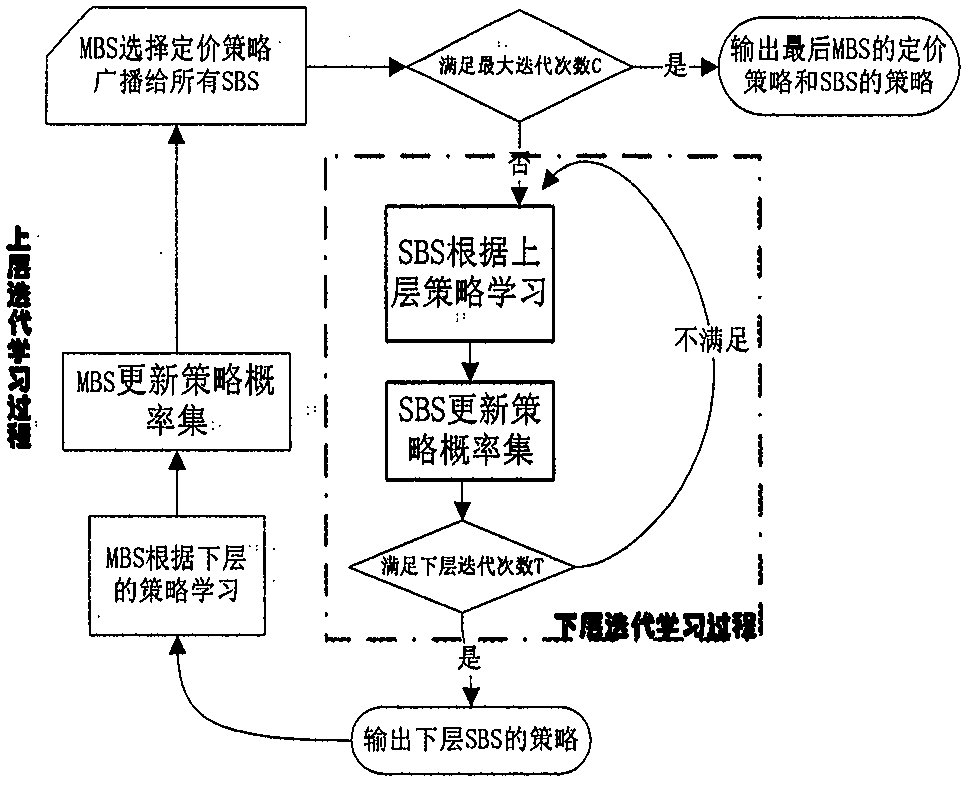
:隨著新媒體數據應用需求的不斷增長,5G蜂窩網絡相對於現在的4G蜂窩網在容量上要提高1000倍,密集組網技術將成為下一代通信的關鍵技術之一。通過在宏蜂窩基站(Macro-cellBaseStation,MBS)周圍布設小蜂窩基站(Small-cellBaseStation,SBS),能夠擴展覆蓋區域,改善能量效率,提高用戶傳輸速率,以達到提高用戶體驗的目的。異構雙層蜂窩網主要有兩種用頻方式:(1)正交獨享模式(split-spectrum),這種方式各級蜂窩相互之間無幹擾,管理簡單但是頻譜效率很低。(2)分享復用模式(shared-spectrum),這種方法可增加頻譜的空間重用效率,更適用於大規模布設的小微蜂窩網絡,但會引起小蜂窩與主蜂窩間的跨層幹擾以及小蜂窩間的同層幹擾,需要幹擾的控制協調。如果不進行適當的幹擾協調,會帶來基站間的嚴重幹擾和發射功率的巨大浪費。因此,幹擾控制協調問題成為了現階段異構無線網資源分配的難點。博弈論是一種用於處理參與者相互間利益決策的方法,適合解決由理性參與者組成的系統優化問題,可廣泛應用於解決多用戶網絡的資源分配問題,如功率和信道的分配。雙層斯坦伯格博弈(StackelbergGame)被廣泛應用於分析和解決分層無線網的資源分配問題。然而現有的博弈資源分配研究都是假設所有用戶和基站間信道狀態信息(ChannelStateInformation,CSI)己知,並據此做相應的決策。但是在實際情況下,特別在異構雙層網絡中,由於基站屬於不同的運營商,基站之間的信息交換很難實現,即便可以獲得,信道信息也具有時效性。另外,出於個人隱私和安全的考慮,基站在雙層網絡中並不願意形成聯盟交換信息,這樣要求協調所有基站的中心式資源分配模式很難落實。因此,如何分布式處理不完美信道信息條件下的異構雙層網絡資源分配是個棘手的問題。現有文獻大都是基於完美信道信息的假設,所有涉及的參數和目標函數都可以準確獲得。由於無線信道的隨機動態特性,現有模型中不同層級間的基站用戶完美獲取相互信息並不實際。但在不確定條件下,使用以往在完美信道信息條件下得到的資源分配策略很可能使實際系統的性能惡化。另外現有工作大都是考慮連續數值的資源分配問題。相比連續的資源分配策略,離散策略的資源分配方式可簡化傳輸設計和數據處理,降低基站之間的信息交換開銷,如在3GPPLTE蜂窩網絡中就只支持離散功率控制的下行傳輸,現有的離散策略選擇方法運算複雜度普遍較高,無法適應實時變化的環境和用戶的決策需要。三技術實現要素:本發明主要目的在於克服現有資源分配方式的上述缺點,提出了一種信道狀態不確定模型下分層異構微蜂窩網絡中的無線資源雙層分配優化框架及一種分布式分層學習算法。提出了方案以實現宏基站和微基站的均衡離散策略搜索。有效抑制由於信道狀態不確定引起的收益下降問題。本發明的目的是由以下技術方案實現的:本發明基於下行鏈路的OFDM分層蜂窩網絡,該網絡由一個宏基站和N個小蜂窩基站組成,如圖1所示。每個蜂窩間通過數字用戶線(DigitalSubscriberLine,DSL)連結,作為控制信道用來交換信息。每個基站以時分復用的方式服務多個用戶。宏基站和小蜂窩基站分享復用網絡頻譜資源。為便於分析,假設每個小蜂窩基站在一個時隙只服務一個小蜂窩用戶。因為小蜂窩基站與宏基站使用相同的頻譜,就不可避免的發生不同基站間的跨層和同層幹擾。為了保護宏基站內用戶的通信質量,我們使用幹擾價格對下層小蜂窩基站的發射功率加以約束,並限定小蜂窩基站對宏基站的累積幹擾必須小於門限值Z。這樣以來,如果下層小蜂窩基站的通信對宏基站造成影響,它就要為對宏基站帶來的幹擾付出代價,所以小蜂窩基站需要優化自己的功率策略。而上層宏基站希望在對其用戶的幹擾限定在滿足服務約束的條件下,儘可能提高對下層小蜂窩基站幹擾收費的總收益。我們採用基於斯坦伯格博弈的雙層構架。上層博弈參與者作為leader,具有強勢地位,首先做出決策並向下層廣播。下層參與者follower是跟隨關係,根據上層的決策被動做出回應,從可能的策略集中選擇對自己最有利的策略。本發明採用單leader多follower形式。MBS作為leader首先行動,發布單位幹擾定價。SBS作為follower,根據上層MBS的定價,選擇最優功率分配策略來最大化其效用。該效用體現博弈參與者對選擇策略的收益,可通過基於策略的函數來表示。該方法的具體步驟如下:1.下層小蜂窩效用分析和表示在異構的無線網絡中,出於理性自私,SBS間不會協商,都是獨立的選擇使自己收益最大的策略,從而構成了非合作博弈關係。我們定義下層用戶SBS的效用函數由速率容量收益、付出的能量代價和對上層的幹擾代價組成。由於是否考慮MBS對SBS幹擾,並不影響問題的分析過程。為便於處理,本發明不涉及宏蜂窩的功率控制問題。所以,下層用戶的收益與自己的發射功率、鄰居SBS對其的幹擾和信道狀態有關。對於下層小微蜂窩,SBSi接收到的信幹噪比可寫為:γi(pi,p-i)=pihiiΣjipjhji+σ0,i{1,2,...,N},---(1)]]>式(1)中σ0代表接收的高斯噪聲功率,pi表示下層SBSi的發射功率,p-i表示除了SBSi外的其他SBS的功率策略,hji表示SBSj對SBSi用戶幹擾的信道增益,i,j∈{1,2,...,N},N為SBS的總數,則代表使用同頻信道的其他基站對SBSi帶來的幹擾。下層SBSi的效用函數可以定義為:ui(pi,p-i,ui,λ0)=Wlog(1+γi(pi,p-i))-uipi-λ0gi0pi(2)式(2)由3部分組成,分別表示SBS的容量收益,功耗代價和SBS對MBS帶來的幹擾,其中W表示帶寬,gi0表示SBSi對MBS用戶的信道增益,ui是能耗單位定價,λ0單位幹擾定價,相當於SBS要為對MBS的幹擾付費。2.上層宏蜂窩效用分析和表示對於上層MBS,其目標是在自身能夠容忍幹擾的條件下(比如所有SBS對MBS宏蜂窩用戶的累積幹擾不超過門限Z),最大化下層SBS對其幹擾的累加付費收益。所以上層MBS的效用函數可以定義為:U0(λ0,pi)=ΣiNλ0gi0pi---(3)]]>式(3)中pi可以表示為關於幹擾定價的函數。它也是上下雙層策略選擇的博弈焦點,暗示了下層SBS發射多少功率與上層的幹擾定價有關。3.已知信道狀態信息時的上下層蜂窩的優化問題對於下層小蜂窩而言,如果SBS要增加其傳輸功率,雖然提高了信號傳輸速率的收益,但將會引起對MBS的幹擾和自身能量的消耗而付出更多的代價。所以下層用戶必須選擇合適的功率策略最大化自己的效用,以達到收益和代價的平衡。對於每個SBS用戶而言,問題可建模為:問題1:MBS要在其幹擾可承受的範圍內最大化自身收益,所以上層的目標可建立為帶約束優化問題,即:問題2:4.幹擾信道狀態信息不完全可知時的魯棒性優化問題由於SBS和MBS隸屬不同的私人或運營商,回程鏈路容量十分有限的,通常無法得到完美的CSI。另外SBS間也缺乏相應機制分享CSI。因此,本發明考慮更加實際的不完美信道信息條件,引入信道不確定模型描述無線信道的隨機動態性。假設基站只知道自己的信道增益hii,但並不確切知道同層幹擾的信道增益hji和跨層幹擾的信道增益gi0。我們把信道增益表示為標稱估計值和不確定值的求和形式,即本文從信道信息不確定引起的最差情況出發,將斯坦伯格博弈問題轉化為雙層的最大最小化問題。下層SBS的效用函數可轉化為:maxminUi(pi,p-i,ui,λ0)=Wlog(1+pihiiΣjipj(hji+Δhji)+σ0)-uipi-λ0(gi0+Δgi0)pi---(6)]]>類似的,上層MBS的效用函數轉化為:maxminU0(λ0,pi)=ΣiNλ0(gi0+Δgi0)pis.t.ΣiN(gi0+Δgi0)pi≤Z---(7)]]>利用柱形模型(column-wise)和柯西不等式,信道增益不確定分量的上界及由不確定所帶來的最大幹擾可分別表徵為:|Δgi0|≤εi0(8-1)ΣjipjΔhji≤Σji|pj|2Σji|Δhji|212≤jiΣjipj2---(8-2)]]>其中ε表示不確定上界。利用公式(8),原問題可轉化為在考慮信道最大不確定情況下的魯棒雙層博弈問題,即式(6)和式(7)的最大最小化問題可被簡化為:問題3:問題4:5.分布式雙層Q學習算法在發明所提的雙層博弈框架中,每個參與博弈的用戶都有有限離散策略集合。本發明將利用強化Q學習算法來找到均衡解。我們假設所有博弈參與人都是理性的,會選擇使其效用最大的最優策略。定義用戶i的可用策略集為|Si|表示策略集的個數。具體到上下層用戶,下層SBS用戶的策略集為上層MBS用戶的策略集為所有用戶的策略空間可表示為代表笛卡爾積。定義其在第t次迭代時,各策略概率矢量為需滿足每個用戶的策略集概率和這樣,用戶i的期望效用就可以表示為:ui(πit,π-it)=EUi|πit,π-it=Σs′SUi(s′)ΠiN∪{0}πi,ait---(11)]]>其中表示用戶i基於目前的策略概率集選出的策略。那麼對於上層MBS的最大化效用目標可寫為:問題5:相似的,對於下層SBS最大化其效用可寫為:問題6:通過上述分析,我們給出雙層強化學習算法的SE定義。定義2:當任意策略選擇同時滿足上下層基站效用和時,則策略選擇是雙層學習的穩定策略解。定理2:在上層MBS給定π0的情況下,下層SBS一定存在一個混合策略解(πi,π-i,π0)滿足從而得到下層的納什均衡。在Q學習過程中,用戶的策略被參數化為Q函數,它表示每個特定策略的相對效用。定義用戶i在第t次迭代時基於策略概率所選的策略的Q函數為通過用戶之間的策略和環境交互,得到每個策略的相應回報獎勵,更新Q函數。在選擇策略後,相應的Q值通過式(21)更新,Qit+1(si,ait+1)=(1-κit)Qit(si,ait)+κitui(si,ait,π-it),---(14)]]>其中代表學習速率,滿足是用戶i在第t次迭代選擇策略的期望回報,如式(15)所示。ui(si,ait,π-it)=Σa-itS-iUi(si,ait,S-it)ΠjN∪{0}/iπj,ajt,---(15)]]>其中且每個BS用戶根據式(15)的玻爾茲曼分布來更新其策略。πit(si,ai)=expQit(si,ait)/ψiΣaiSexpQit(si,ait)/ψi,---(16)]]>其中ψi>0是溫度係數,用來控制策略選擇是傾向探測還是利用。當ψi趨於0,表示用戶只利用,會選擇相應的策略去最大化Q值。相對地,當ψi趨於∞,表示用戶只探測,用戶的策略選擇是完全隨機的,用戶的策略概率分布滿足均勻分布。根據式(14)和(16),上層MBS通過迭代更新對應Q函數。假設上層MBS每c時段更新一次定價策略。在雙層學習迭代算法中,作為唯一的公共信息,上層的MBS首先向下層所有SBS發布定價。下層接收到幹擾價格後,通過學習算法找到各自的最優響應功率策略,然後在每個時間段終點反饋回上層MBS,以便上層MBS根據下層上報的功率策略信息更新自己的出價策略。算法是嵌套迭代循環方式。下層SBSi的Q函數通過式(17)更新,Qit+1(si,ait+1)=(1-κit)Qit(si,ait)+κitui(si,ait,s0,a0),---(17)]]>其中估計的期望效用可表示為:其中表示在一個時間段內上下層合併選擇為的次數。我們可看到上層MBS和下層SBS的更新是基於不同的時間單位的,下層用戶每T時隙更新迭代完成一次,而上層用戶c個時間段更新迭代完成一次,上下層用戶策略的更新都是基於對方迭代更新後的結果通過Q學習得到的。下層在每個時隙結束時執行式(17),完成其Q函數的更新。類似的,上層MBS用戶在每個時間段c結束時執行式(19),完成其Q函數的更新:Q0c+1(s0,a0)=(1-κ0)Q0c(s0,a0)+κ0u0c(s0,a0,π-icT)---(19)]]>在實際算法運行過程中,當用戶的策略集相對較大時,收斂的速度將指數增加,成為很大的短板。本發明所提算法充分利用每次的環境信息,在一次迭代更新所有策略的Q值,算法能很快收斂到一個純策略均衡點,具體步驟如表1所示。表1改進型雙層Q學習算法本發明的有益效果如下:在保護宏基站內用戶的通信質量的前提下,提出的異構雙層魯棒模型能有效抑制由於不確定度變化帶來的用戶收益減少的問題。所提算法能夠在較短時間收斂並獲取優越的策略選擇結果。四附圖說明圖1為下行鏈路的OFDM蜂窩網絡的系統示意圖;圖2為雙層Q學習算法流程圖;圖3為所建框架性能說明示意圖;五具體實施方式本發明實施例如圖1所示,該網絡由一個宏基站和2個小蜂窩基站組成。每個基站以時分復用的方式服務多個用戶。宏基站和小蜂窩基站分享復用網絡頻譜資源。為便於分析,假設每個小蜂窩基站在一個時隙只服務一個小蜂窩用戶。1)下層小蜂窩效用分析和表示ui(pi,p-i,ui,λ0)=Wlog(1+pihiiΣjipjhji+σ0)-uipi-λ0gi0pi]]>由3部分組成,分別表示SBS的容量收益,功耗代價和SBS對MBS帶來的幹擾,其中W表示帶寬,σ0代表接收的高斯噪聲功率,pi表示下層SBSi的發射功率,p-i表示除了SBSi外的其他SBS的功率策略,hji表示SBSj對SBSi用戶幹擾的信道增益,則代表使用同頻信道的其他基站對SBSi帶來的幹擾。gi0表示SBSi對MBS用戶的信道增益,ui是能耗單位定價,λ0單位幹擾定價,相當於SBS要為對MBS的幹擾付費。下層用戶必須選擇合適的功率策略最大化自己的效用,以達到收益和代價的平衡。對於每個SBS用戶而言,問題可建模為:問題1:2)上層宏蜂窩效用分析和表示u0(λ0,pi)=ΣiNλ0gi0pi]]>MBS要在其幹擾可承受的範圍內最大化自身收益,所以上層的目標可建立為帶約束優化問題,即:問題2:3)幹擾信道狀態信息不完全可知時的魯棒性優化問題本發明利用信道不確定模型描述無線信道的隨機動態性。基站可通過信道測量技術(channel-qualityindicatormeasure)獲得自己的信道增益hii,但並不確切知道同層幹擾的信道增益hji和跨層幹擾的信道增益gi0。我們把信道增益表示為標稱估計值和不確定值的求和形式,即本文從信道信息不確定引起的最差情況出發,將斯坦伯格博弈問題轉化為雙層的最大最小化問題。並利用柱形模型(column-wise)和柯西不等式,信道增益不確定分量的上界及由不確定所帶來的最大幹擾可分別表徵為:|Δgi0|≤εi0ΣjipjΔhji≤Σji|pj|2Σji|Δhji|212≤jiΣjipj2]]>其中ε表示不確定上界。利用以上公式,原問題可轉化為在考慮信道最大不確定情況下的魯棒雙層博弈問題,建模問題1,2的最大最小化問題可被簡化為:問題3:問題4:4)分布式雙層Q學習算法假設SBS1和SBS2對MBS用戶的標稱信道增益分別為g10=0.2,g20=0.3,歸一化SBS對其自身用戶的信道增益為h1,1=h2,2=1,下層SBS間的標稱幹擾信道增益分別是h1,2=h2,1=0.1。噪聲功率σ0=0.01dBmW。設MBS的幹擾價格策略集為π0=[2.5,3,3.5,4,4.5],SBS的功率分配策略集為其中SBS的最大傳輸功率pmax=100dBmW。設置每個時間段由T=100個時隙組成,上層迭代時間段數C=100。步驟1:開始上層循環,直到c=C最大時間段數。(初始化所有用戶Q函數為各策略等概率分布。)(1)在每個時間段開始,MBS根據其策略概率集π0,選擇一個定價策略並廣播給所有的下層SBS。步驟2:下層學習過程t=1:T(1)每個SBSi根據自己的策略概率集選擇各自功率策略si,ai。(2)每個SBSi根據反饋信息計算其效用並根據式更新其估計期望效用(3)每個SBSi根據式計算其他|Si|-1個策略的效用(4)每個SBSi根據式和式更新其Q值和策略概率集。(5)所有SBS把最後策略傳給MBS在T時隙結束。完成下層策略的迭代更新。步驟3:MBS計算其第c個時間段的效用步驟4:MBS根據式和式更新其Q值和策略概率集。步驟5:MBS根據其已更新的策略概率集選擇上層策略。完成上層策略的迭代更新。c=c+1,跳回到步驟1。迭代結束,輸出1個宏蜂窩和2個小蜂窩基站的相應最佳策略。當前第1頁1 2 3 
