用於計算結構的電磁散射性質和近似結構的重構的方法和設備與流程

2023-06-13 08:10:01 1

用於計算結構的電磁散射性質和近似結構的重構的方法和設備相關申請的交叉引用本申請要求2013年9月9日提交的美國臨時申請61/875,340的優先權，並且該申請通過引用全部合併於此。技術領域本申請涉及結構的電磁散射性質的計算。本發明可以例如在微觀結構的量測中應用，例如以評估光刻設備的臨界尺寸(CD)性能。

背景技術：
光刻設備是將期望的圖案施加到襯底上、通常是到襯底的目標部分上的機器。可以例如在集成電路(IC)的製造中使用光刻設備。在這種情況下，備選地稱作掩模或掩模版的圖案形成裝置可以用於生成待形成在IC的單個層上的電路圖案。該圖案可以被轉移到襯底(例如，矽晶片)上的目標部分(例如，包括裸片的一部分、一個或數個裸片)上。圖案的轉移典型地是憑藉到設置於襯底上的一層輻射敏感材料(抗蝕劑)上的成像來進行。一般情況下，單個襯底將含有相繼地被圖案化的相鄰目標部分的網絡。已知的光刻設備包括：所謂的步進器，其中通過使整個圖案一次曝光到目標部分上來輻照各目標部分；和所謂的掃描器，其中通過在給定方向(「掃描」方向)上憑藉輻射束掃描圖案同時同步地平行於或反向平行於該方向掃描襯底來輻照各目標部分。也可以通過將圖案壓印到襯底上而使圖案從圖案形成裝置轉移至襯底。為了監測光刻工藝，有必要測量被圖案化的襯底的參數，例如形成在其中或其上的相繼的層之間的重疊誤差。存在有用於進行在光刻工藝中形成的微觀結構的測量的各種技術，包括掃描電子顯微鏡和各種專用工具的使用。一種形式的專用檢查工具是其中輻射的光束被引導到襯底的表面上的目標上並且測量散射的或反射的光束的性質的散射儀。通過將光束的在由襯底反射或散射之前和之後的性質進行比較，可以確定襯底的性質。這可以例如通過將反射的光束與存儲在與已知襯底性質相關聯的已知測量的庫中的數據進行比較來完成。兩種主要類型的散射儀是已知的。光譜散射儀將寬頻帶輻射束引導到襯底上並且測量被散射到特定的窄角度範圍內的輻射的光譜(作為波長的函數的強度)。角分辨散射儀使用單色輻射束並測量作為角度的函數的散射的輻射的強度。更一般地，能夠將散射的輻射與在數學上從結構的模型預測的散射行為進行比較將是有用的，結構的模型可以自由地設定和變化直到預測的行為與來自真實樣本的觀察到的散射匹配。不幸的是，雖然如何通過數值程序對散射建模在原理上是已知的，但已知技術的計算負擔致使這樣的技術不實用，特別是如果期望實時重構的話，和/或當牽涉到的結構與在一維上周期性的簡單結構相比更加複雜時。CD重構屬於在逆散射的一般名稱下已知的一組問題，其中觀察到的數據和可能的物理狀況匹配。目的是找到引出儘可能密切地觀察到的數據的物理狀況。在散射測量的情況中，電磁理論(麥克斯韋方程)允許預測什麼將是針對給定物理狀況的測量出的(散射的)數據。這被稱為前向散射問題(forwardscatteringproblem)。逆散射問題現在是找到對應於實際測量出的數據的適當物理狀況，這典型地是高度非線性問題。為求解該逆散射問題，使用了使用許多前向散射問題的解的非線性求解器。在用於重構的已知手段中，非線性問題建立在三個要素上：·在測量出的數據與從估計的散射設定計算出的數據之間的差異的高斯-牛頓最小化；·在散射設定中的參數化形狀，例如接觸孔的半徑和高度；·每次參數更新時前向問題(例如，計算出的反射係數)的解中的充分高的準確度。對於1D-或2D-周期性結構(例如光柵)的CD重構，可以使用體積分法(VIM)以有效地計算出有關散射問題的解，如已在美國專利申請公開號US2011/0218789A1和美國專利申請公開號US2011/0098992A1中公開的，這些申請通過引用合併於此。對於在周期性的平面中的光譜展開的特定選擇造成在正交非周期性方向上的完全解耦模態的描述。採取各具有描述每個模式的波傳播的1D格林函數的一維積分方程的序列形式的該模態描述被離散或採樣以獲得數值方案。對於低階離散化方案，1D積分方程的結構導致用於矩陣-矢量乘積的數值上穩定且有效的O(N)算法，其中N是每個1D積分方程的樣本的數量。切比雪夫展開(Chebyshevexpansion)已知道了很長一段時間並且尤其是其與離散餘弦變換(DCT)的關係已被採用以產生用於包括微分方程和1D積分方程、例如[2,4,5]的一系列數值方法的有效的數值方案。使1D積分方程離散的低階展開的明顯缺點在於數值離散化誤差收斂為O(h2)，其中h是網格尺寸。對於沿著非周期性方向關于波長高的結構，許多樣本都需要達到可接受的準確度水平，這進而導致長的計算時間和大的存儲器要求。用以增加收斂率的手段接著引入具有高階多項式的較高階展開，這引出了包括切比雪夫多項式展開和勒讓德多項式展開(Legendrepolynomialexpansion)的偽譜方法。偽譜方法因其指數收斂而聞名。然而，利用該手段存在有兩點警告：高階展開引出有效的矩陣-矢量乘積嗎？；和，所得數值方案穩定嗎？切比雪夫展開由於離散餘弦變換(DCT)的使用而產生O(NlogN)的有效的矩陣-矢量乘積。然而，穩定性結果成了大問題、尤其是對於衰逝模式(evanescentmode)而言，例如[2]中呈現出的方案已發現對於上面提到的積分方程是高度不穩定的，如在本文中的圖16中圖示出的。在沒有用於穩定性的進一步措施的情況下，積分方程的所得線性系統具有非常高的條件數並因此不能被迭代地可靠求解。

技術實現要素：
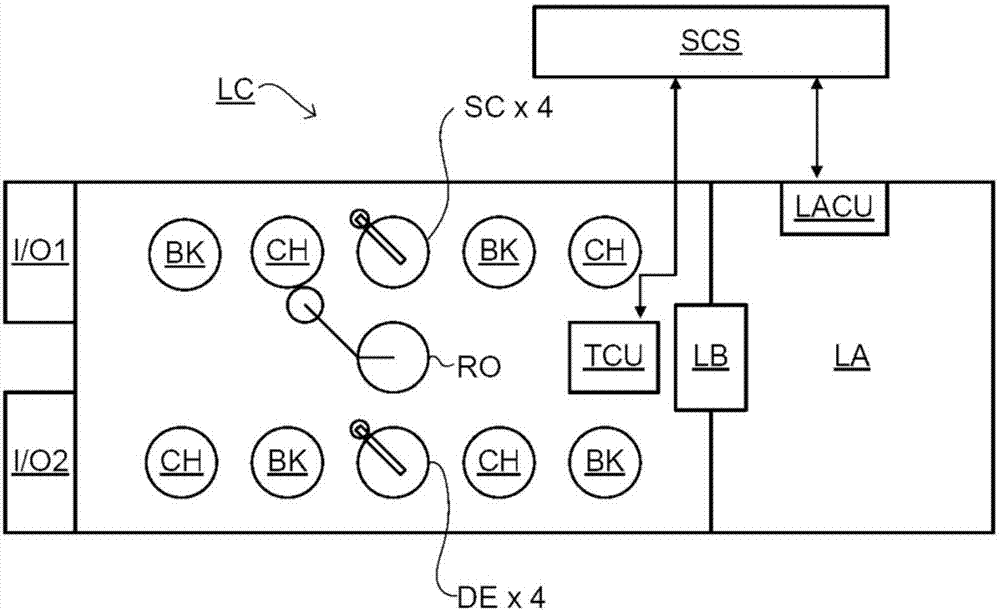
在半導體工藝的領域期望的是迅速地執行電磁散射性質的準確計算。根據本發明的第一方面，提供有一種計算結構的電磁散射性質的方法，該結構包括不同性質的材料並且該結構在至少一個橫向方向上是周期性的並在相對於至少一個橫向方向正交的方向上延伸，該方法包括：-通過針對在至少一個橫向方向上的多個模式中的每個相應模式執行在正交方向上的偽譜多項式展開乘以對於多個模式中的所有模式都使用在正交方向上的相同樣本點的1D格林函數的積分，針對多個模式在數值上求解用於電磁散射的體積分方程，其中積分通過求解方程的正則化線性系統來執行；和-使用數值求解的結果來計算結構的電磁散射性質。方法可以進一步包括如下步驟：-通過藉助限定擴展的正則化展開係數矢量(γ1,γ2)修改線性系統以補償易於發生與條件調節相關的誤差的展開係數而將方程的線性系統正則化；-求解在第一離散變換步驟與第二離散變換步驟之間的方程的正則化線性系統以計算出正則化展開係數矢量(γ1,γ2)的值；-將第二離散變換步驟應用於正則化展開係數矢量(γ1,γ2)的非擴展部分以計算出在正交方向上的樣本點處的正則化積分(H1(k)和H2(k))；和其中計算結構的電磁散射性質的步驟使用計算出的正則化積分(H1(k)和H2(k))。使方程的線性系統正則化的步驟可以包括生成在正交方向上的樣本點處的函數(F(k))，函數包括易於產生與條件調節相關的誤差的展開係數，使得線性系統的修改補償函數(F(k))，並且方法可以進一步包括在離散轉換步驟之後的、將正則化積分(H1(k)和H2(k))與正則化展開係數矢量(γ1,γ2)的擴展部分(γ1M+1,γ2M+1)乘以函數(F(k))組合以計算出在正交方向上的樣本點處的進一步的積分(G1(k)和G2(k))的步驟，並且其中計算結構的電磁散射性質的步驟可以使用計算出的進一步的積分(G1(k)和G2(k))。根據本發明的第二方面，提供有一種從由通過輻射照射對象而產生的檢測到的電磁散射性質重構對象的近似結構的方法，方法包括如下步驟：-估計至少一個結構參數；-從至少一個結構參數確定至少一個模型電磁散射性質；-將檢測到的電磁散射性質與至少一個模型電磁散射性質進行比較；和-基於比較的結果來確定近似對象結構，其中模型電磁散射性質使用根據任一前述權利要求的方法來確定。根據本發明的第三方面，提供有一種用於重構對象的近似結構的檢查設備，檢查設備包括：-照射系統，被配置成用輻射照射對象；-檢測系統，被配置成檢測由照射產生的電磁散射性質；和-處理器，被配置成：-估計至少一個結構參數；-從至少一個結構參數確定至少一個模型電磁散射性質；-將檢測到的電磁散射性質與至少一個模型電磁散射性質進行比較；和-從檢測到的電磁散射性質與至少一個模型電磁散射性質之間的差異來確定近似對象結構，其中處理器被配置成使用根據第一方面的方法來確定模型電磁散射性質。根據本發明的第四方面，提供有一種電腦程式產品，含有用於計算結構的電磁散射性質的計算機可讀指令的一個或多個系列，指令適於引起一個或多個處理器執行根據權利要求1至7中的任一個的方法。發明的進一步特徵和優點、以及發明的各種實施例的結構和操作在下面參照附圖詳細地進行描述。需要注意的是發明不限於在這裡所描述的特定實施例。一些實施例在這裡被呈現僅用於圖示性目的。附加實施例對於相關領域(多個)技術人員而言基於在這裡所含的教導是顯而易見的。附圖說明被包含在這裡並形成說明書的一部分的附圖圖示出本發明並且與描述一起進一步用於說明發明的原理並使得(多個)相關領域技術人員能夠做出並使用發明。圖1描繪了光刻設備。圖2描描繪了光刻單元或簇。圖3描繪了第一散射儀。圖4描描繪了第二散射儀。圖5描繪了使用用於從散射儀測量進行的結構的重構的本發明的實施例的第一示例過程。圖6描繪了使用用於從散射儀測量進行的結構的重構的本發明的實施例的第二示例過程。圖7描繪了可以根據本發明的實施例被重構的散射幾何結構。圖8描繪了背景的結構。圖9圖示出用以計算入射場與分層介質的相互作用的格林函數的使用。圖10是針對對比電流密度、電場或由電場和電通量密度的線性組合構成的矢量場求解對應於VIM公式的線性系統的高級方法的流程圖。圖11是根據本發明的實施例的針對電場使用VIM公式的更新矢量的計算的流程圖。圖12描繪了使用連續的矢量場以在數值上求解VIM公式的本發明的實施例；圖13是根據本發明的實施例的更新矢量的計算的流程圖；圖14描繪了根據本發明的實施例的求解具有對比源反演的VIM公式的方法。圖15是根據本發明的實施例的使用了具有對比源反演的VIM公式的更新矢量的計算的流程圖。圖16圖示出在對數刻度上的對應於針對一維電介質平板的VIM公式的離散版本的線性系統的條件數相對於傳播係數的實部乘厚度以及相對於展開的多項式次數PD。圖17A和圖17B是根據本發明的實施例的方法的流程圖。圖18以示意性形式描繪了配置有程序和數據以便執行根據本發明的方法的計算機系統。本發明的特徵和優點將從下面結合附圖時闡述的詳細描述中變得更加顯而易見，其中相似的參考字符始終標識出相應的元件。在附圖中，相似的參考數字一般指示出同樣的、功能上類似的和/或結構上類似的元件。元件首次出現所在的附圖用相應參考數字中的最左側位數指示出。具體實施方式該說明書公開了包含該發明的特徵的一個或多個實施例。所公開的實施例(多個)僅舉例說明了本發明。本發明的範圍不限於所公開的實施例(多個)。本發明由所附的權利要求限定。所描述的實施例和說明書中對「一個實施例」、「實施例」、「示例實施例」等的引用指示出所描述的實施例(多個)可以包括特定的特徵、結構或特性，但是每個實施例可以並不一定包括特定的特徵、結構或特性。此外，這樣的短語並不一定是指相同實施例。此外，當特定的特徵、結構或特性是與實施例有關地描述時，可以理解的是，與無論是否明確地描述的其他實施例有關地實現這樣的特徵、結構或特性是在本領域技術人員的知識內的。本發明的實施例可以在硬體、固件、軟體或它們的任何組合中實施。本發明的實施例也可以被實施為可由一個或多個處理器讀取和執行的存儲在機器可讀介質上的指令。機器可讀介質可以包括用於存儲或傳輸呈可由機器(例如，計算裝置)讀取的形式的信息的任何機構。例如，機器可讀介質可以包括只讀存儲器(ROM)；隨機存取存儲器(RAM)；磁碟存儲介質；光存儲介質；快閃記憶體裝置；電、光、聲或其他形式的傳播信號(例如，載波、紅外信號、數位訊號等)，及其他。此外，固件、軟體、例行程序、指令可以在這裡被描述為執行某些動作。然而，應該領會的是，這樣的描述僅為了方便並且這樣的動作事實上產生於執行固件、軟體、例行程序、指令等的計算裝置、處理器、控制器或其他裝置。然而，在更詳細地描述這樣的實施例之前，呈現出可以實施本發明的實施例的示例環境是有指導性的。圖1示意性地描繪了光刻設備。設備包括：照射系統(照射器)IL，被配置成調節輻射束B(例如，UV輻射或DUV輻射)；支撐結構(例如，掩模臺)MT，被構造成支撐圖案形成裝置(例如，掩模)MA並被連接至配置成根據某些參數將圖案形成裝置準確定位的第一定位器PM；襯底臺(例如，晶片臺)WT，被構造成保持襯底(例如，塗有抗蝕劑的晶片)W並被連接至配置成根據某些參數將襯底準確定位的第二定位器PW；和投影系統(例如，折射式投影透鏡系統)PL，被配置成將通過圖案形成裝置MA賦予輻射束B的圖案投影到襯底W的目標部分C(例如，包括一個或多個裸片)上。照射系統可以包括各種類型的光學部件，如折射型、反射型、磁性型、電磁型、靜電型或其他類型的光學部件，或者它們的任何組合，用於引導、成形或控制輻射。支撐結構支撐著圖案形成裝置、即支承其重量。它以取決於圖案形成裝置的定向、光刻設備的設計和諸如例如圖案形成裝置是否被保持在真空環境中等的其他條件的方式來保持圖案形成裝置。支撐結構可以使用機械的、真空的、靜電的或其他夾持技術來保持圖案形成裝置。支撐結構可以是例如可根據需要固定或可動的框架或臺。支撐結構可以確保圖案形成裝置例如相對於投影系統處於期望的位置。這裡關於術語「掩模版」或「掩模」的任何使用都可以視為與更上位的術語「圖案形成裝置」同義。這裡使用的術語「圖案形成裝置」應該廣義地解釋為是指可以用於在輻射束的截面中賦予輻射束以圖案以便在襯底的目標部分中創建出圖案的任何裝置。應該注意的是，賦予輻射束的圖案可以不是精確地對應於襯底的目標部分中的期望圖案，例如，如果圖案包括相移特徵或所謂輔助特徵的話。一般地，賦予輻射束的圖案將對應於諸如集成電路等的正在目標部分中創建的器件中的特定的功能層。圖案形成裝置可以是透射型的或反射型的。圖案形成裝置的示例包括掩模、可編程反射鏡陣列和可編程LCD面板。掩模是光刻中公知的，並且包括諸如二元、交替相移和衰減相移等的掩模類型，以及各種混合掩模類型。可編程反射鏡陣列的示例採用小反射鏡的矩陣布置，其中的每一個能夠單獨地傾斜以便沿不同方向反射進來的輻射束。傾斜的反射鏡在由反射鏡矩陣反射的在輻射束中賦予圖案。這裡使用的術語「投射系統」應該被廣義地解釋為涵蓋任何類型的投影系統，包括折射型、反射型、反射折射型、磁性型、電磁型和靜電型光學系統，或它們的任何組合，視正使用的曝光輻射或諸如浸沒液體的使用或真空的使用等的其他因素的情況而定。術語「投影透鏡」的任何使用在這裡可以視作與更上位的術語「投影系統」同義。如這裡所描繪的，設備是透射類型的(例如，採用透射式掩模)。備選地，設備可以是反射類型的(例如，採用如上面所提及的類型的可編程反射鏡陣列，或者採用反射式掩模)。光刻設備可以是具有兩個(雙級)或更多襯底臺(和/或兩個或更多的掩模臺)的類型的。在這樣的「多級」機器中，可以並行地使用附加的臺，或者可以在一個或多個臺上執行預備步驟同時一個或多個其他臺被用於曝光。光刻設備也可以是如下類型的：其中，襯底的至少一部分可以由具有相對高的折射率的液體、例如水覆蓋，以便填充投影系統與襯底之間的空間。浸沒液體也可以施加至光刻設備中的其他空間，例如在掩模與投影系統之間。浸沒技術是現有技術中公知的，用於增加投影系統的數值孔徑。如這裡使用的術語「浸沒」不意味著諸如襯底等的結構必須被沉浸在液體中，反而僅意味著在曝光期間在投影系統與襯底之間設有液體。參見圖1，照射器IL從輻射源SO接收輻射束。源和光刻設備可以是單獨的實體，例如當源是受激準分子雷射器時。在這樣的情況中，源不視為形成光刻設備的一部分，並且在包括了例如合適的引導反射鏡和/或擴束器的光束傳遞系統BD的幫助下使輻射束從源SO傳到照射器IL。在其他情況中，源可以是光刻設備的一體部分，例如當源是汞燈時。源SO和照射器IL以及如果需要的話與光束傳遞系統BD一起可以稱作照射系統。照射器IL可以包括用於調整照射光束的角強度分布的調整器AD。一般地，可以調整照射器的光瞳面中的強度分布的至少外徑向範圍和/或內徑向範圍(常分別稱作σ外和σ內)。另外，照射器IL可以包括諸如積分器IN和聚光器CO等的各種其他部件。照射器可以用於調節照射光束，以在其截面中具有期望的均勻性和強度分布。輻射束B入射在被保持在支撐結構(例如，掩模臺MT)上的圖案形成裝置(例如，掩模)MA上，並且通過圖案形成裝置而被圖案化。在橫穿過掩模MA之後，輻射束B通過投影系統PL，該投影系統使光束聚焦到襯底W的目標部分C上。在第二定位器PW和位置傳感器IF(例如，幹涉儀裝置、線性編碼器、2-D編碼器或電容傳感器)的幫助下，可以使襯底臺WT準確地移動，例如以便將不同的目標部分C定位在輻射束B的路徑上。類似地，第一定位器PM和另一位置傳感器(圖1中未明確描繪)可以用於將掩模MA相對於輻射束B的路徑準確地定位，例如在從掩模庫進行的機械檢索之後，或在掃描期間。一般情況下，掩模臺MT的移動可以在形成第一定位器PM的一部分的長行程模塊(粗略定位)和短行程模塊(精細定位)的幫助下實現。類似地，襯底臺WT的移動可以利用形成第二定位器PW的一部分的長行程模塊和短行程模塊來實現。在步進器(與掃描器相對)的情況中，掩模臺MT可以僅連接至短行程致動器，或者可以是固定的。掩模MA和襯底W可以利用掩模對準標記M1、M2和襯底對準標記P1、P2而對準。雖然如圖示出的襯底對準標記佔據了專用目標部分，但它們可以位於目標部分之間的空間中(這些被稱為劃線對準標記)。類似地，在超過一個的裸片設置於掩模MA上的情況下，掩模對準標記可以位於裸片之間。所描繪的設備可以以下面的模式中的至少一個使用：1.在步進模式中，使掩模臺MT和襯底臺WT保持基本靜止，而將賦予輻射束的整個圖案一次投影到目標部分C上(即，單次靜態曝光)。接著使襯底臺WT在X和/或Y方向上移位使得不同的目標部分C能夠被曝光。在步進模式中，曝光場的最大尺寸限制了在單次靜態曝光中成像的目標部分C的尺寸。2.在掃描模式中，同步地掃描掩模臺MT和襯底臺WT而同時將賦予輻射束的圖案投影到目標部分C上(即，單次動態曝光)。襯底臺WT相對於掩模臺MT的速度和方向可以由投影系統PL的(縮小)放大率和圖像反轉特性來確定。在掃描模式中，曝光場的最大尺寸限制了單次動態曝光中的目標部分的寬度(在非掃描方向上的)，而掃描運動的長度確定了目標部分的高度(在掃描方向上的)。3.在另一模式中，使掩模臺MT保持基本靜止地保持著可編程的圖案形成裝置，並且在將賦予輻射束的圖案投影到目標部分C上的狀態下移動或掃描襯底臺WT。在該模式中，一般採用脈衝輻射源，並且在襯底臺WT的每次移動之後或在掃描期間的相繼的輻射脈衝之間根據需要更新可編程的圖案形成裝置。該操作模式可以容易地應用於使用諸如上面所提及的類型的可編程反射鏡陣列等的可編程圖像形成裝置的無掩模光刻。也可以採用上面描述的使用模式的組合和/或變化或者完全不同的使用模式。如圖2所示，光刻裝置LA形成有時也稱作光刻單元或簇的光刻單元LC的一部分，該光刻單元LC還包括用以在襯底上執行曝光前和後工藝的設備。傳統上，這些設備包括用以沉積抗蝕劑層的旋塗器SC、用以使已曝光的抗蝕劑顯影的顯影器DE、激冷板CH和烘烤板BK。襯底機械手或機器人RO從輸入/輸出埠I/O1、I/O2拾取襯底、使它們在不同工藝設備之間移動並接著傳遞至光刻設備的進料臺LB。經常總稱為軌道的這些裝置在軌道控制單元TCU的控制之下，該軌道控制單元TCU自身由監督控制系統SCS控制，該監督控制系統SCS還憑藉光刻控制單元LACU控制著光刻設備。因此，可以操作不同設備以使生產量和處理效率最大化。為了使通過光刻設備被曝光的襯底正確且一致地曝光，期望檢查已曝光的襯底以測量諸如隨後的層之間的重疊誤差、線厚度、臨界尺寸(CD)等的性質。如果檢測到誤差，則可以對隨後的襯底的曝光度進行調整，尤其是如果檢查可以即刻且快速地完成足以使相同批次的其他襯底仍然待曝光的話。還有，已經被曝光的襯底可以被剝離並重新加工—以提高產率—或丟棄，由此避免在已知會有缺陷的襯底上執行曝光。在襯底的僅一些目標部分有缺陷的情況中，可以僅在良好的那些目標部分上執行進一步的曝光。檢查設備用於確定襯底的性質，並且特別是確定不同襯底或相同襯底的不同層的性質從層到層是如何變化的。檢查設備可以一體化到光刻設備LA或光刻單元LC內或者可以是獨立的裝置。為了使得能夠實現最迅速的測量，期望的是檢查設備在曝光之後立即測量在已曝光的抗蝕劑層中的性質。然而，抗蝕劑中的潛像具有非常低的對比度—在抗蝕劑的已曝光於輻射的部分與未曝光的那些部分之間在反射率上僅有非常小的差異—並且不是所有檢查設備都具有用以進行潛像的有用測量的充分的敏感度。因此可以在曝光後烘烤步驟(PEB)之後進行，該曝光後烘烤步驟習慣上是在已曝光的襯底上所進行的第一步驟並且增加抗蝕劑的已曝光和未曝光部分之間的對比度。在該階段，抗蝕劑中的圖像可以被稱作半潛。也可以進行已顯影的抗蝕劑圖像的測量—此時抗蝕劑的已曝光的或者未曝光的部分已被去除—或者在諸如蝕刻等的圖案轉移步驟之後進行。後一可能性限制了有缺陷襯底的重新加工的可能性但仍然可以提供有用信息。圖3描繪了可以在本發明的實施例中使用的散射儀。它包括將輻射投影到襯底W上的寬頻帶(白光)輻射投影器2。反射的輻射被傳至光譜儀檢測器4，其測量鏡面反射的輻射的光譜10(作為波長的函數的強度)。從該數據，可以通過處理單元PU、例如傳統上通過嚴格耦合波分析(RCWA)和非線性回歸或者如圖3的底部所示通過與模擬光譜的庫進行的比較來重構引出檢測到的光譜的結構或輪廓。一般情況下，對於重構，結構的一般形式是已知的並且從做出結構所使用的工藝的知識假設一些參數，僅留下結構的幾個參數待由散射測量數據確定。這樣的散射儀可以被配置為正入射散射儀或斜入射散射儀。可以在本發明的實施例中使用的另一散射儀被示出在圖4中。在該裝置中，由輻射源2發射出的輻射使用透鏡系統12被聚焦通過幹涉濾波器13和偏振器17、由部分反射表面16反射並且憑藉具有高數值孔徑(NA)、優選至少0.9並且更優選至少0.95的顯微鏡物鏡15被聚焦到襯底W上。浸沒式散射儀可以甚至具有有著超過1的數值孔徑的透鏡。反射的輻射接著透射通過部分反射表面16進入檢測器18內以便使散射光譜被檢測。檢測器可以位於在透鏡系統15的焦距上的背投影光瞳平面11中，然而光瞳平面可以替代地利用輔助光學器件(未示出)被重新成像到檢測器上。光瞳平面是其中輻射的徑向位置限定入射的角度並且角位置限定輻射的方位角度的平面。檢測器優選為二維檢測器，使得襯底目標30的二維角散射光譜可以被測量。檢測器18可以例如是CCD或CMOS傳感器的陣列，並且可以使用例如每幀40毫秒的積分時間。參考光束經常例如用於測量入射輻射的強度。要做到這一點，當輻射束入射在分束器16上時，它的一部分透射通過分束器作為朝向參考反射鏡14的參考光束。參考光束接著被投影到相同檢測器18的不同部分上。一組幹涉濾波器13是可用的以選出在比方說405nm至790nm或甚至更低、如200nm至300nm的範圍中的所感興趣的波長。幹涉濾波器可以是可調諧的而不是包括一組不同的濾波器。可以使用光柵代替幹涉濾波器。檢測器18可以以單個波長(或窄波長範圍)測量散射光的強度、以多個波長單獨地測量強度或測量在波長範圍之上集成的強度。此外，檢測器可以單獨地測量橫向磁與橫向電偏振光的強度和/或橫向磁與橫向電偏振光之間的相位差。使用寬頻帶光源(即，具有寬範圍的光頻率或波長的光源—並因此是寬範圍的顏色)是可能的，其給出了大的集光率，從而允許了多個波長的混合。寬頻帶中的多個波長優選地各具有Δλ的帶寬和至少2Δλ(即，帶寬的兩倍)的間距。輻射的數個「源」可以是使用纖維束已分裂開的擴展輻射源的不同部分。以該方式，可以並行地以多個波長測量角分辨散射光譜。3-D光譜(波長和兩個不同的角度)可以被測量，其含有與2-D光譜相比更多的信息。這允許更多信息被測量，這增加了量測過程穩健性(robustness)。這在EP1,628,164A中更詳細地進行了描述。襯底W上的目標30可以是光柵，其被印刷成使得在顯影之後，條紋由實的抗蝕劑線形成。條紋可以備選地被蝕刻到襯底內。該圖案對光刻投影設備、特別是投影系統PL中的色差敏感，並且照射對稱性和這樣的像差的存在將使它們自身顯現在被印刷的光柵上的變化中。於是，被印刷的光柵的散射測量數據被用於重構光柵。光柵的諸如線寬和形狀等的參數可以從印刷步驟和/或其他散射測量過程的知識被輸入至由處理單元PU執行的重構過程。建模如上所述，目標是在襯底的表面上。該目標經常採取在光柵中的一系列的線或者2-D陣列中的大致矩形結構的形狀。量測中的嚴格光學衍射理論的目的是有效地計算從目標反射的衍射光譜。換言之，針對CD(臨界尺寸)均勻性和重疊量測得到目標形狀信息。重疊量測是其中兩個目標的重疊被測量以便確定襯底上的兩個層是否對準的測量系統。CD均勻性是簡單地光柵在光譜上的均勻性的測量以確定光刻設備的曝光系統是如何起作用的。具體地，CD或臨界尺寸是被「寫入」襯底上的對象的寬度並且是光刻設備在物理上能夠在襯底上寫入的限制。與諸如目標30等的目標結構的建模及其衍射性質結合地使用上面所描述的散射儀中的一個，可以以若干方式來執行結構的形狀和其他參數的測量。在由圖5表示的第一類型的過程中，計算出基於目標形狀(第一候選結構)的第一估計的衍射圖案並且與觀察到的衍射圖案進行比較。接著使模型的參數系統地變化並且在一系列的迭代中重新計算出衍射，以生成新的候選結構並因此獲得最佳擬合。在由圖6表示的第二類型的過程中，事先計算出針對許多不同候選結構的衍射光譜，以創建衍射光譜的「庫」。接著將從測量目標觀察到的衍射圖案與計算出的光譜的庫進行比較以找到最佳擬合。兩種方法可以一起使用：可以從庫得到粗略擬合，隨後通過迭代過程找到最佳擬合更詳細地參見圖5，將簡要描述執行目標形狀和/或材料性質的測量的方式。目標將對於該描述被假設為一維(1-D)結構。在實踐中它可以是一維的，並且處理將相應地進行調節。在步驟502中，使用諸如上面所描述的那些等的散射儀來測量襯底上的實際目標的衍射圖案。該測量出的衍射圖案被轉發至諸如計算機等的計算系統。計算系統可以是上面提及的處理單元PU，或者它可以是單獨的設備。在步驟503中，建立在若干參數pi(p1、p2、p3等等)方面限定目標結構的參數化模型的「模型選配方案」。這些參數可以在1D周期性結構中例如表示側壁的角度、特徵的高度或深度、特徵的寬度。目標材料和底下的層的性質也用諸如折射率(在散射測量輻射束中存在的特定的波長處)等的參數表示。下面將給出特定示例。重要的是，雖然目標結構可以由描述其形狀和材料性質的幾十個參數限定，但模型選配方案會將這些參數中的許多限定為具有固定值，而其他的是可變或「浮動」參數，用於以下過程步驟的目的。此外下面我們描述做出固定和浮動參數之間的選擇所使用的過程。此外，我們將引入其中可以準許參數變化而沒有完全獨立的浮動參數的方式。為了描述圖5的目的，僅可變參數被視作參數pi。在步驟504中：通過設定用於浮動參數的初始值pi(0)(即，p1(0)、p2(0)、p3(0)等等)估計模型目標形狀。將在某些預定範圍內生成各浮動參數，如選配方案中限定的。在步驟506中，例如使用諸如RCWA等的嚴格光學衍射方法或者麥克斯韋方程的其他任何求解器，將表示估計形狀的參數與模型的不同元件的光學性質一起用於計算散射性質。這給出了估計目標形狀的估計或模型衍射圖案。在步驟508和510中，接著將測量出的衍射圖案與模型衍射圖案進行比較，並且它們的類似之處和差異用於計算出針對模型目標形狀的「評價函數」。在步驟512中，假設評價函數指示出模型在它準確地表示實際目標形狀之前需要改進，估計新的參數p1(1)、p2(1)、p3(1)等并迭代反饋到步驟506中。重複步驟506至512。為了幫助搜索，步驟506中的計算可以進一步生成評價函數的偏導數，指示出增加或減小參數將使評價函數在參數空間中的該特定的區域中增加或減小時所採用的靈敏度。評價函數的計算和導數的使用一般是本領域已知的，並且將不會在這裡詳細描述。在步驟514中，當評價函數指示出該迭代過程已收斂在具有期望準確度的解上時，將當前估計參數報告作為實際目標結構的測量。該迭代過程的計算時間很大程度上由所使用的前向衍射模型來確定，即利用嚴格光學衍射理論從估計目標結構進行的估計模型衍射圖案的計算。如果要求更多參數，那麼有更多的自由度。計算時間在原理上以自由度的數量的冪增加。在506計算出的估計或模型衍射圖案可以以各種形式表達。如果以與步驟510中生成的測量出的圖案相同的形式表達計算出的圖案，則使比較簡化。例如，模型化光譜可以很容易與由圖3的設備測量出的光譜進行比較；模型化光瞳圖案可以很容易與由圖4的設備測量出的光瞳圖案進行比較。從圖5向前遍及該描述，將在使用圖4的散射儀的假設下使用術語「衍射圖案」。本領域技術人員將容易使教導適於不同類型的散射儀，或者甚至其他類型的測量儀器。圖6圖示出備選的示例過程，其中事先計算出針對不同估計目標形狀(候選結構)的多個模型衍射圖案並且存儲在庫中用於與真實測量進行比較。下面的原理和術語與用於圖5的過程相同。圖6的過程的步驟是：在步驟602中，執行生成庫的過程。可以針對各類型的目標結構生成單獨的庫。庫可以由測量設備的用戶根據需要生成，或者可以由設備的供應商預先生成。在步驟603中，建立在若干參數pi(p1、p2、p3等等)方面限定目標結構的參數化模型的「模型選配方案」。迭代過程的考慮類似於步驟503中的那些。在步驟604中，例如通過生成所有參數的隨機值，來生成參數p1(0)、p2(0)、p3(0)的第一集合等，各參數都在其值的預期範圍內。在步驟606中，計算出模型衍射圖案並存儲在庫中，表示從由參數表示的目標形狀所預期的衍射圖案。在步驟608中，生成參數p1(1)、p2(1)、p3(1)等的新集合。步驟606、608重複數十、數百或甚至數千次，直到包括所有存儲的模型化衍射圖案的庫被判定充分完成。各存儲的圖案表示多維參數空間中的樣本點。庫中的樣本應該以充分的密度填充樣本空間，使得任何真實衍射圖案都將被充分密切地被表示。在步驟610中，在生成庫之後(雖然可以在之前)，將真實目標30放置在散射儀中並測量出其衍射圖案。在步驟612中，將測量出的圖案與存儲在庫中的模型化圖案進行比較以找到最佳匹配圖案。可以與庫中的每一個樣本進行比較，或者可以採用更系統的搜索策略，以降低計算負擔。在步驟614中，如果找到匹配，那麼用於生成匹配的庫圖案的估計目標形狀可以被確定為近似對象結構。對應於匹配的樣本的形狀參數被輸出作為測量出的形狀參數。匹配過程可以直接在模型衍射信號上執行，或者它可以在被優化用於快速評估的替代模型上執行。在步驟616中，可選地，使用最近的匹配樣本作為起始點，並且使用細化過程以得到用於報告的最終參數。該細化過程可以包括例如與圖5中示出的那個非常類似的迭代過程。是否需要細化步驟616對於實施者是個選擇的問題。如果庫被非常密集地採樣，那麼迭代細化可以不需要，因為總會找到良好的匹配。另一方面，這樣的庫可能對於實際使用太大。實用的解決方案因此是使用庫搜索參數的粗略集合，隨後是使用評價函數以確定參數的更準確集合的一次或多次迭代，以報告具有期望準確度的目標襯底的參數。當執行附加迭代時，將是添加計算出的衍射圖案及相關聯的經過細化的參數集合作為庫中的新條目的選項。以該方式，可以初始使用庫，這基於相對小的計算工作量，但這構建了使用細化步驟616的計算工作量的較大庫。無論使用哪種方案，所報告的可變參數中的一個或多個的值的進一步細化也可以基於多個候選結構的匹配的優度得到。例如，最終報告的參數值可以通過兩個或多個候選結構的參數值之間的插值產生，假設這些候選結構的兩者或所有都具有高的匹配分數。該迭代過程的計算時間很大程度上由在步驟506和606的前向衍射模型來確定，即利用嚴格光學衍射理論從估計目標形狀進行的估計模型衍射圖案的計算。對於2D周期性結構的CD重構，在前向衍射模型中常使用RCWA，而微分方法、體積分方法(VIM)、有限差分時域(FDTD)和有限元法(FEM)也已有報導。如例如用在RCWA和差分方法中的傅立葉級數展開也可以通過採用完美匹配層(PML)或者用以模仿朝向無限接近在其上使用傅立葉展開的單位單元的邊界的輻射的其他類型的吸收邊界條件而用於解析非周期性結構。體積分方法RCWA的主要問題之一是它要求用於2D周期性結構的大量的中央處理單元(CPU)時間和存儲器，因為一個序列的特徵值/特徵矢量問題需要求解和串接。對於FDTD和FEM，CPU時間典型地也是太高。已知的體積分方法(如美國專利號6,867,866B1和美國專利號7,038,850B2中所公開的)或者基於展現出相對於網格細化的緩慢收斂的全空間離散化方案，或者基於展現出相對于越來越多的諧波的差的收斂的光譜離散化方案。作為可替代方案，提出了包含啟發式方法以改善收斂的光譜離散化方案。對於VIM而言必須求解的線性系統與RCWA相比大得多，但是如果它以迭代方式求解，則與數個矢量的存儲一起僅需要矩陣-矢量乘積。因此，存儲器使用典型地比用於RCWA的低得多。潛在瓶頸是矩陣-矢量乘積自身的速度。如果在VIM中應用Li規則、也稱作傅立葉因子分解規則，那麼矩陣-矢量乘積將會歸因於數個逆子矩陣的存在而慢得多。備選地，Li規則可以忽略並且FFT可以被用於獲得快速矩陣-矢量乘積，但差的收斂的問題依然存在。圖7示意性地圖示出可以根據本發明的實施例被重構的散射幾何結構。襯底702是在z方向上分層的介質的較低部分。示出了其他層704和706。在x和y上周期性的二維光柵708被示出在分層介質的頂部。還示出了x、y和z軸710。入射場712與結構702至708相互作用並被它們散射，從而造成反射場714。因此結構在至少一個方向x、y上是周期性的並且包括不同性質的材料，以便在包括了不同材料之間的材料邊界處的入射電磁場分量Einc和散射電磁場分量ES的總和的電磁場Etot上引起間斷。圖8示出背景的結構並且圖9示意性地圖示出可以用於計算入射場與分層介質的相互作用的格林函數。在圖8和圖9中，分層介質702至706對應於與圖7中相同的結構。在圖8中，也連同入射場712示出了x、y和z軸710。還示出了直接反射場802。參照圖9，點源(x』，y』，z』)904表示格林函數與生成場906的背景的相互作用。在該情況中，因為點源904在頂部層706的上方，所以有來自706與周圍介質的頂部接口的僅一個背景反射908。如果點源在分層介質內，那麼將會有在上、下方向兩者上的背景反射(未示出)。待求解的VIM公式是Jc(x',y',z')＝χ(x',y',z')Etot(x',y',z')(0.2)在該方程中，入射場Einc是已知的入射的角度、偏振和幅值的函數，Etot是未知的並且計算解所針對的總電場，Jc是對比電流密度，是格林函數(3×3矩陣)，χ是由jω(ε(x,y,z,)-εb(z))給出的對比度函數，其中ε是結構的介電常數並且εb是背景介質的介電常數。χ在光柵外是零。格林函數是已知的並且針對包括702至706的分層介質可計算。格林函數示出了在xy平面中的卷積和/或模態分解(m1,m2)並且在中沿著z軸的佔優勢的計算負擔是卷積。對於離散化，總電場在xy平面中以布洛赫/弗洛凱模式(Bloch/Floquetmode)展開。與χ的乘法變成：(a)在xy平面中的離散卷積(2DFFT)；和(b)在z上的乘積。在xy平面中的格林函數相互作用是每個模式的相互作用。對應於均質背景介質的在z上的格林函數相互作用是可以利用具有複雜性O(NlogN)的一維(1D)FFT執行的卷積。備選地，但圖中未示出，在z上的格林函數可以通過採用具有複雜性O(N)的憑藉在z上的向上和向下遞推關係的其半可分離(semi-separability)性質來計算。通過將已經計算出的結果的一部分重新使用作為用於均質背景介質的相互作用的一部分，可以添加來自在光柵上方和下方的分層介質的反射的貢獻。xy中的模式的數量是M1M2，並且z中的樣本的數量是N。有效的矩陣-矢量乘積具有複雜性O(M1M2Nlog(M1M2N))並且存儲複雜性是O(M1M2N)。使用基於克雷洛夫子空間方法(Krylovsubspacemethod)、例如BiCGstab(l)(穩定雙共軛梯度法)的迭代求解器來執行對於Ax＝b的VIM解方法，BiCGstab(l)典型地具有步驟：將殘餘誤差限定為rn＝b–Axn憑藉殘餘誤差計算出更新矢量(多個)vn更新解：xn+1＝xn+αnvn更新殘餘誤差rn+1＝rn-αnAvn圖10是求解對應於VIM公式的線性系統的高級方法的流程圖。這是通過在數值上求解體積分計算出結構的電磁散射性質的方法。在最高級，第一步驟是預處理1002，包括讀取輸入並準備FFT。下一步驟是計算出解1004。最後，執行在其中計算出反射係數的後處理1006。步驟1004包括也示出在圖10的右手側的各種步驟。這些步驟是計算入射場1008、計算格林函數1010、計算更新矢量1012、更新解與殘餘誤差(例如，使用BiCGstab)1014和測試看看是否達到收斂1016。如果未達到收斂，則控制環路返回至作為更新矢量的計算的步驟1012。圖11圖示出根據本發明的實施例的使用了體積分方法的在對應於圖10的步驟1012的計算更新矢量中的步驟，該方法是通過在數值上求解針對電場E的體積分方程計算出結構的電磁散射性質的方法。步驟1102是在四維(4D)陣列中重組矢量。在該陣列中第一維度具有三個元素Ex、Ey和Ez。第二維度具有針對m1的所有值的元素。第三維度具有針對m2的所有值的元素。第四維度具有針對z的所有值的元素。因此4D陣列存儲了總電場(Ex,Ey,Ez)(m2,m2,z)的光譜(在xy平面中)表示。在圖11中從步驟1102下降的三個並行的虛線箭頭對應於通過針對各層z而執行的步驟1104至1110進行的三個2D陣列的處理，每個陣列分別針對Ex、Ey和Ez。這些步驟執行電場(Ex,Ey,Ez)(m2,m2,z)的光譜(在xy平面中)表示與材料性質的卷積以計算出對應於下面的方程(0.2)的對比電流密度(m1,m2,z)的光譜(在xy平面中)表示。詳細地，步驟1104牽涉到取出三個2D陣列(二維是針對m1和m2)。在步驟1106中，將2DFFT針對三個陣列中的每一個前向計算成空間域。在步驟1108中，將三個陣列中的每一個乘以通過傅立葉表示的截短被過濾的對比度函數χ(x,y,z)的空間表示。在步驟1110中完成卷積，其中2DFFT後向到產生光譜對比電流密度(m1,m2,z)的光譜(在xy平面中)域。在步驟1112中將計算出的光譜對比電流密度放回到4D陣列中。接著針對各模式(即，在相同時間針對z中的所有樣本點)，執行步驟1114至1122。從步驟1116旁邊下降的三個虛線箭頭對應於計算積分項，該積分項是背景與自身是由總電場的與結構的相互作用而產生的對比電流密度的相互作用。這已知是使用光譜域(相對於z方向)中的乘法通過(m1,m2,z)與空間(相對於z方向)格林函數的卷積來執行。然而，根據本發明的實施例，偽譜多項式展開乘以1D格林函數的積分通過求解方程的正則化的線性系統來執行。可以求解兩個正則化的系統：一個用於向上積分並且一個用於向下積分。在兩倍大的一個矩陣方程下可以帶來兩個非耦合的系統。方程的線性系統可以通過藉助限定擴展的正則化展開係數矢量修改線性系統以補償易於發生與條件調節相關的誤差的展開係數而被正則化。使方程的線性系統正則化可以包括生成在正交方向上的樣本點的函數F(k)，函數包括易於發生與條件調節相關的誤差的展開係數，使得線性系統的修改補償了函數F(k)。詳細地，在步驟1114中，取出光譜對比電流密度(m1,m2,z)作為針對x、y和z中的每一個的三個1D陣列。步驟1116至步驟1120牽涉到在第一和第二離散變換步驟1116與1120之間將方程的正則化線性系統求解1118成正則化展開係數矢量γ的值。包括步驟1116至1120的虛線方框1150對應於參照提供了更詳細的描述的圖17A和圖17B所描述的步驟。在步驟1122中，添加相對於z在空間域中的背景反射(參見圖9中的908)。背景反射與格林函數的該分離是傳統技術並且步驟可以通過添加軼-1投影來執行，如本領域技術人員應該領會的。當處理各模式時，接著在步驟1124中將如此計算出的針對總電場(Ex,Ey,Ez)(m2,m2,z)的更新矢量放回到4D陣列中。下一步驟是在矢量中重組4D陣列1126，該步驟與「在4D陣列中重組矢量」的步驟1102的不同之處在於它是反向運算：使各一維索引與四維索引唯一地相關。最後在步驟1128中，從輸入矢量中減去來自步驟1126的矢量輸出，對應於方程(0.1)的右手側中的減法。輸入矢量是在圖11中的步驟1102中進入的並且含有(Ex,Ey,Ez)(m1,m2,z)的輸入矢量。利用圖11中所描述的方法的問題在於它導致差的收斂。該差的收斂由介電常數上的並行跳動和針對截短的傅立葉空間表示的對比電流密度引起。如上面所討論的，在VIM方法中Li逆規則不適於克服收斂問題，因為在VIM中逆規則的複雜性由於VIM數值求解中所需的非常大量的逆運算而導致非常大的計算負擔。通過引用合併於此的美國專利申請公開號US2011/0218789A1公開了一種克服了由並行跳動引起的收斂問題而不用訴諸如Li所描述的逆規則的使用的方式。通過避免逆規則，US2011/0218789A1的手段不用犧牲用於在VIM手段中以迭代方式求解線性系統所要求的矩陣-矢量乘積的效率。US2011/0218789A1公開了在計算結構的電磁散射性質的體積分方法(VIM)中的改進的收斂通過在數值上求解針對矢量場F而不是電場E的體積分方程來獲得。矢量場F可以通過基的改變而與電場E相關，並且可以在電場E具有間斷的材料邊界處是連續的。矢量場F的卷積使用根據有限勞倫規則的卷積算子(根據有限離散卷積運算)來執行，這允許了憑藉1D和/或2DFFT(快速傅立葉變換)的有效矩陣-矢量乘積。可逆的基卷積與改變算子C被配置成通過執行根據周期性結構的材料和幾何性質的基的改變將矢量場F變換成電場E。在求解了針對矢量場F的體積分之後，附加的後處理步驟可以用於從矢量場F得到電場E。矢量場F可以通過使用法向-矢量場n濾除連續分量而由電場E與電通量密度D的場分量的組合構成。改進的體積分方法可以被包含到用於重構對象的近似結構的量測工具中的前向衍射模型內、例如以評估光刻設備的臨界尺寸(CD)性能。圖12圖示出使用連續矢量場在數值上求解VIM公式的本發明的實施例。這牽涉到針對通過基的改變與電場E相關的矢量場F在數值上求解體積分方程，矢量場F在一個或多個材料邊界處是連續的，以便確定矢量場F的近似解。矢量場F通過相對於至少一個方向x，y的至少一個有限傅立葉級數來表示，並且在數值上求解體積分方程的步驟包括通過矢量場F與基卷積與改變算子C的卷積來確定電場E的分量，和通過矢量場F與卷積算子M的卷積來確定電流密度J。基卷積與改變算子C是可逆的並且包括在至少一個方向x、y上的結構的材料和幾何性質，並且被配置成通過執行根據材料和幾何性質的基的改變而將矢量場F變換成電場E。卷積算子M包括在至少一個方向x、y方向上的結構的材料和幾何性質。電流密度J可以是對比電流密度並且通過相對於至少一個方向x、y的至少一個有限傅立葉級數來表示。卷積使用諸如從包括第一傅立葉變換(FFT)和數論變換(NTT)的集合中選出的一個等的變換來執行。基卷積與改變算子C和卷積算子M根據有限離散卷積運算，以便產生有限結果。圖12示出了針對中間矢量場F求解VIM系統的步驟1202，以及用以通過矢量場F的近似解與基卷積與改變算子C的卷積而得到總電場E的後處理步驟1204。卷積可以使用諸如從包括快速傅立葉變換(FFT)和數論變換(NTT)的集合中選出的一個等的變換來執行。圖12還在右手側示出了執行有效矩陣-矢量乘積1206至1216以迭代地求解VIM系統的示意性圖示。這起始於步驟1206中的中間矢量場F。第一次設定此F，它可以從零開始。在此初始步驟之後，通過迭代求解器和殘餘引導F的估計。接下來，使用憑藉針對z方向上的各樣本點的2DFFT的基卷積與改變算子C與中間矢量場F的卷積來計算出1208總電場E。基卷積與改變算子C被配置成將中間矢量場F的基變換成總電場E的基。還有，對比電流密度J是在步驟1210中使用材料卷積算子M與中間矢量場F的卷積而計算出。步驟1210是利用憑藉2DFFT執行的卷積而針對z中的各樣本點而執行。在步驟1212中，計算出在格林函數G與對比電流密度J之間的相互作用和軼-1投影以產生散射電場Es。運算1214將兩個計算出的結果Es從E中減去以得到Einc的近似值1216。因為步驟1206至1216產生更新矢量，於是後處理步驟1204被用於產生總電場E的最終值。與單獨的後處理步驟1204不同，所有更新矢量的總和可以在步驟1208處被記錄以便計算出總電場E。然而，此手段增加了方法的存儲要求，而後處理步驟1204與迭代步驟1206至1216相比在存儲或處理時間上成本低。因此，在圖12的左手側上，指定出對應於光譜VIM的線性系統。線性系統憑藉迭代求解器和圖12的右手側上的流程圖中指定出的VIM的有效矩陣-矢量乘積來求解。本發明的實施例關係到矩陣-矢量乘積流程圖的右手側上的方塊1212「計算Es＝-G*J」。該方塊評估歸因於對比電流密度J的散射電場Es。根據本發明的實施例，在該方塊中，偽譜多項式展開乘以1D格林函數的積分通過求解方程的正則化線性系統來執行。以與參照圖11所討論的方式相同的方式，可以求解兩種正則化系統：一個用於向上積分並且一個用於向下積分。可以在兩倍大的一個矩陣方程下帶來兩個未耦合的系統。方程的線性系統可以通過藉助限定擴展的正則化展開係數矢量修改線性系統以補償易於發生與條件調節相關的誤差的展開係數而被正則化。使方程的線性系統正則化可以包括生成在正交方向上的樣本點的函數F(k)，函數包括易於發生與條件調節相關的誤差的展開係數，使得線性系統的修改補償了函數F(k)。矩陣-矢量乘積的該部分的計算是基於在(非均勻)切比雪夫柵格上採樣的針對量J的切比雪夫展開乘以用於1D亥姆霍茲方程(Helmholtzequation)的1D格林函數的閉合形式解析積分。憑藉用於閉合切比雪夫規則的離散餘弦變換(DCT)(即，I型DCT)，將J的採樣值變換成用於切比雪夫展開的係數。隨後，通過求解解析正則化線性系統將展開積分，其中在這裡所描述的解析正則化是第一次用於計算傅立葉積分的應用。後一步驟造成表示與格林函數積分之後的結果的用於新切比雪夫展開的係數的集合。作為最終步驟，在相同的非均勻切比雪夫柵格上評估展開。虛線方塊1250對應於由參照圖13描述的虛線方框1350所圍成的步驟和參照圖17A和圖17B描述的步驟。與以前的手段的明顯差異在於這裡所描述的實施例可以不只是解決單個1D積分方程，而且可以解決1D積分方程或單個積分的完整系統，對此耦合歸因於在縱向方向上在相同柵格上評估出的場-材料相互作用而發生。縱向方向是正交於結構是周期性所在的橫向方向(例如x，y)的「非周期性」或「正交」方向。這裡所描述的實施例在相同時間在用於所有模式的一個算法內解決了效率和穩定性兩者。圖13是基於US2011/0218789A1的公開的根據本發明的實施例的更新矢量的計算的流程圖。圖13的流程圖對應於圖12的右手側(步驟1206至1216)。在步驟1302中，在4D陣列中重組矢量。接著針對z中的各樣本點執行步驟1304至1318。在步驟1304中，從4D陣列中取出三個2D陣列。這三個2D陣列(Ft1,Ft2,Fn)(m1,m2,z)分別對應於連續矢量場F的兩個切向分量Ft1、Ft2和法向分量Fn，各分量具有對應於m1和m2的兩個維度。因此矢量場F通過使用法向-矢量場n濾除電磁場E的相切於至少一個材料邊界的連續分量並且還濾除電磁通量密度D的垂直於至少一個材料邊界的連續分量而由電磁場E與相應電磁通量密度D的場分量的組合構成。在步驟1306中，用(Ft1,Ft2,Fn)(m1,m2,z)表示的光譜連續矢量場的卷積起始於用(Ft1,Ft2,Fn)(x,y,z)表示的在步驟1306中的2DFFT前向的針對三個陣列中的每一個到空間域內的計算。在步驟1308中，將從步驟1306得到的傅立葉變換(Ft1,Ft2,Fn)(x,y,z)在空間域中乘以空間乘法算子C(x,y,z)。在步驟1310中，將在步驟1308中得到的乘積通過2DFFT後向變換成光譜域。接著在步驟1312處將光譜總電場(Ex,Ey,Ez)放回4D陣列中。此外，將副本反饋前向至下面討論的減法運算1322。在步驟1314中，將從步驟1306得到的傅立葉變換(Ft1,Ft2,Fn)(x,y,z)在空間域中乘以乘法算子M。在步驟1316中通過2DFFT後向將在步驟1314中的計算的乘積變換成光譜域以產生用(m1,m2,z)表示的光譜對比電流密度。在步驟1318中將光譜對比電流密度放回4D陣列中。為了完成已知入射電場Einc的近似值的計算，以與參照圖11中的相應識別編號的步驟所描述的方式相同的方式、通過步驟1114至1122針對各模式m1、m2計算出格林函數與背景的相互作用。如參照圖11所描述的，步驟1116至1120牽涉到在第一與第二離散變換步驟1116與1120之間求解1118方程的正則化線性系統以計算出正則化展開係數矢量γ的值。因此包括步驟1116至1120的虛線方框1350對應於參照提供了更詳細描述的圖17A和圖17B描述的步驟。在步驟1320中，將背景與光譜對比電流密度J的光譜格林函數的相互作用的結果放回4D陣列中。最後，在步驟1322中，利用從由步驟1312前向反饋的總電場中減去步驟1320的結果的減法來完成已知入射電場Einc的近似值的計算，並且最終步驟1314在矢量中重組4D陣列。這意味著4D陣列的每一個四維索引與矢量的一維索引唯一地相關。通過引用合併於此的美國專利US2013/0066597A1公開了一種適於在量測應用中重構光柵輪廓的對比-源反演(CSI)算法。實施例牽涉到在數值上求解針對電流密度J的體積分方程。它通過E與J的線性組合的連續分量的選擇而採用與電場ES相關的矢量場FS和電流密度J的隱式構造，矢量場F在一個或多個材料邊界處連續，以便確定電流密度J的近似解。矢量場F用相對於至少一個方向x、y的至少一個有限傅立葉級數來表示，並且數值上求解體積分方程的步驟包括通過矢量場F與卷積算子M的卷積來確定電流密度J的分量。卷積算子M包括在x、y方向上的結構的材料和幾何性質。電流密度J可以用相對於x、y方向的至少一個有限傅立葉級數來表示。此外，連續分量可以使用作用於電場E和電流密度J的卷積算子PT和Pn來提取。圖14圖示出基於US2013/0066597A1的公開的本發明的另一實施例。圖14示出通過採用使用連續分量提取算子形成的中間矢量場F來求解針對電流密度J的VIM系統的步驟1402，以及用以通過使格林函數算子作用於電流密度J得到總電場E的後處理步驟1404。圖14還在右手側示出了執行有效矩陣-矢量乘積1406至1420以迭代地求解VIM系統的示意性圖示。這起始於步驟1406中的電流密度J。第一次設定此J，它可以從零開始。在此初始步驟之後，通過迭代求解器和殘餘引導J的估計。在步驟1408中，計算出在格林函數G與對比電流密度J之間的相互作用和軼-1投影以產生散射電場Es。根據本發明的實施例，通過求解方程的正則化線性系統來執行偽譜多項式展開的積分。以與參照圖11和圖12所討論的方式相同的方式，可以求解兩個正則化系統：一個用於向上積分並且一個用於向下積分。可以在兩倍大的一個矩陣方程下帶來兩個非耦合的系統。方程的線性系統可以通過藉助限定擴展的正則化展開係數矢量修改線性系統以補償易於發生與條件調節相關的誤差的展開係數而被正則化。使方程的線性系統正則化可以包括生成在正交方向上的樣本點的函數F(k)，函數包括易於發生與條件調節相關的誤差的展開係數，使得線性系統的修改補償了函數F(k)。虛線方框1450對應於由參照圖15描述的虛線方框1550所圍住的步驟和參照圖17A和圖17B所描述的步驟。還有，在步驟1414中使用與作用於散射電場Es和電流密度J的兩個連續分量提取算子PT和Pn的卷積來計算出中間矢量場F。因此第一連續分量提取算子PT在步驟1410中被用於提取電磁場Es的連續分量，並且第二連續分量提取算子Pn在步驟1412中被用於提取按比例縮放的電磁通量密度Ds的連續分量。在步驟1416中，場-材料相互作用算子(M)在提取出的連續分量上運算。步驟1414表示從在步驟1410中得到的電磁場的連續分量與在步驟1412中得到的按比例縮放的電磁通量密度的連續分量形成在材料邊界連續的上矢量場Fs。確定對比電流密度的分量的步驟1416通過使用場-材料相互作用算子M在矢量場Fs上運算來執行。步驟1410至1416是利用憑藉FFT執行的卷積針對z中的各樣本點而執行。卷積可以使用諸如從包括快速傅立葉變換(FFT)和數論變換(NTT)的集合中選出的一個等的變換來執行。運算1418將兩個計算出的結果Js從J中減去以得到1420中的與入射電場Einc相關的Jinc的近似值。因為步驟1406至1420產生更新矢量，於是後處理步驟1404被用於產生總電場E的最終值。與單獨的後處理步驟1404不同，所有更新矢量的總和可以在步驟1408處被記錄以便計算出散射電場Es並且後處理步驟變成僅僅將入射電場Einc添加至散射電場。然而，此手段增加了方法的存儲要求，而後處理步驟1404與迭代步驟1406至1420相比在存儲或處理時間上成本低。圖15是基於US2013/0066597A1的根據本發明的實施例的更新矢量的計算的流程圖。圖15的流程圖對應於圖14的右手側(步驟1406至1420)。在步驟1502中在4D陣列中重組矢量。隨後，以與參照圖11中編號1114至1124和圖13中編號1114至1320的相應步驟所描述的方式相同的方式通過步驟1504至1514針對各模式m1、m2計算出格林函數與背景的相互作用。如參照圖11和圖13所描述的，步驟1116至1120牽涉到在第一與第二離散變換步驟1116與1120之間求解1118方程的正則化線性系統以計算出正則化展開係數矢量γ的值。因此包括步驟1116至1120的虛線方框1150對應於參照提供了更詳細描述的圖17A至圖17B描述的步驟。接著針對z中的各樣本點(也就是，針對各層)，執行步驟1516至1530。在步驟1516中，從4D陣列中取出三個2D陣列。這三個2D陣列(Ex,Ey,Ez)(m1,m2,z)對應於散射電場E的笛卡爾分量，各分量具有對應於m1和m2的兩個維度。用(Fx,Fy,Fz)(m1,m2,z)表示的連續矢量場的卷積起始於用(Ex,Ey,Ez)(m1,m2,z)表示的在步驟1518中的2DFFT前向的針對三個陣列中的每一個到空間域內的計算。在步驟1520中，將從步驟1518得到的傅立葉變換(Ex,Ey,Ez)(x,y,z)在空間域中乘以空間乘法算子MPT(x,y,z)，這具有兩個功能：首先通過應用切向投影算子PT濾除散射電場的連續分量，由此產生了連續矢量場F的切向分量，並且其次通過將連續矢量場F與僅關於散射場的對比電流密度J聯繫起來的對比度函數M執行乘法。在步驟1514處將放回4D陣列中的散射場(Ex,Ey,Ez)(m2,m2,z)反饋到如上面所討論的步驟1516和如下面所討論的步驟1522兩者內。在步驟1522中，針對z中的各樣本點(也就是，針對各層)，將散射電通量密度D的按比例縮放的版本形成為從步驟1514得到的散射電場與從取出三個2D陣列之前的步驟1502前向反饋到的對比電流密度的按比例縮放的總和，對應於在光譜域中的D的笛卡爾分量。在步驟1524中，執行這些陣列的2DFFT，產生了在空間域中的笛卡爾分量(Dx,Dy,Dz)(x,y,z)。在步驟1526中，將這些陣列在空間域中乘以乘法算子MPn，這具有兩個功能：首先按比例縮放的通量密度的連續的法向矢量被濾除並且產生連續矢量場F的法向分量，並且其次通過將連續矢量場F與僅關於散射場的對比電流密度J聯繫起來的對比度函數M執行乘法。接著在步驟1528中，將步驟1520與1526的結果組合以產生針對連續矢量場F的所有分量、即切向和法向分量的運算MF的近似值。接著在步驟1530中通過2DFFT後向將MF變換成光譜域以產生用MF(m1,m2,z)表示的光譜對比電流密度的近似值。在步驟1532中，將與散射場相關的所得的光譜對比電流密度返回4D陣列中，並且隨後在步驟1534中轉換回矢量。這意味著使4D陣列的每一個四維索引與矢量的一維索引唯一地相關。最後在步驟1530中，利用從由步驟1502的輸入前向反饋到的總對比電流密度中減去步驟1534的結果的減法來完成與入射電場Jinc相關的已知對比電流密度的近似值的計算。切比雪夫插值算法在實施例中，解決了在計算電磁散射性質的體積分方法中的一維積分方程的序列的沿著縱向非周期性(z)方向上的離散。最初，已利用用於展開對比-電流密度的局部分段線性基函數和用於測試而匹配的點將這些積分方程離散。該手段的優點在於，當採用1D格林函數的半可分離性時導致O(N)的簡單且低複雜性的算法，或者當採用卷積性質時導致O(NlogN)的簡單且低複雜性的算法，其中N是基函數和樣本點的數量。此外，在z方向上的光柵的幾何結構可以由切片建立並且可以對每個切片處理離散。然而，缺點在於，沿著z方向的插值誤差的收斂歸因於分段線性展開函數而限於第二階。這是與其中針對各模式的行為在具有從特徵值分解得出的傳播係數的指數函數方面在解析上是已知的RCWA相比。由於我們不想在體積分方法中引入昂貴的特徵值計算，所以我們在尋找一種在維持用於一維積分方程的序列的低複雜性矩陣-矢量乘積的狀態下導致插值誤差的快速收斂的可替代方案。得到對於插值的較高階收斂的自然方式是使用較高階的多項式基。然而在沿著這些線推理時應該牢記兩個方面。首先，為了得到較高階收斂，待插值的函數應該充分地正則以允許高階插值，即，函數應該可連續微分至在插值的整個區間上充分高的次數。在體積分方法中，這意味著高階插值僅在每個切片被應用，因為對比電流密度的作為在積分方程中的插值函數的光譜分量可以橫跨切片邊界展現出數種間斷。第二方面在於，插值和與插值核、即光譜格林函數的積分應該產生針對相應矩陣-矢量乘積的低複雜性算法。對於低階分段線性展開，這是簡單的，因為各基函數的受限的支持產生低階遞推關係，即，可以憑藉幾個乘法和已經計算出的函數值及積分函數值的添加從一個樣本點積分至下一個。對於較高階多項式，這典型地不是這樣的情況，因為插值點沿著整個插值區間擴散。因此，需要另一機制產生低複雜性矩陣-矢量乘積。這裡所使用的機制在於，可以在與一維格林函數核積分之前和之後的正交多項式的展開係數之間導出僅牽涉到幾個(和固定數量的)以前計算出的係數和權重的短遞推關係，並且多項式的加權和可以憑藉低複雜性算法在恰當選出的特定點處進行評估。特別地，我們選擇可以通過與快速傅立葉變換(FFT)直接相關的離散餘弦變換(DCT)在所謂的切比雪夫節點處被評估的第一種切比雪夫多項式的基。格林函數與積分方程在體積分方法中，要求將表示為jm(z)的對比電流密度的光譜分量與一維格林函數核以及其相對於z的第一和第二導數積分，即，其中i∈{x,y,z}表示對比電流密度的笛卡爾分量，n∈{0,1,2}表示相對於z的微分的階數，並且(微分之後)z呈現獨立於m的預定離散值。這些積分可以被改寫為積分的線性組合其中z∈[a,b]。這些積分方程核所屬的核的類是所謂的半可分離核。這些積分也承擔對沃特拉(Volterra)積分方程的強相似性。由於在向上和向下積分上的積分的分裂，指數函數上的絕對值可以被去除，這產生了表達式雖然現在可以將exp(±γmz)帶到積分外，但在數值意義上實施這一步時需要小心，因為γm可能很大並且是正的而z呈現[a,b]中的值，這可能會造成用於指數的非常大或非常小的數量。第一種切比雪夫多項式上的準備工作為了函數的插值已相當多地使用了第一種切比雪夫多項式，由此形成了所謂的偽譜方法的子類。偽譜方法對於在非常平滑的函數上的相對於插值誤差的其高階收斂是已知的。此外，切比雪夫多項式形成了具有使得它們展現出呈連續函數形式和呈離散(採樣的)函數形式兩者的正交性的特殊性質的正交多項式的集合。它們把這些性質歸功於在以連續和離散傅立葉變換採用時它們與傅立葉展開的親密關係，對於該傅立葉展開連續和離散的正交關係也成立。階數n＝0,1,2,.的第一種切比雪夫多項式Tn(x)在區間x∈[-1,1]上限定為Tn(x)＝cos(narccos(x)).(6)雖然該限定可以擴展超過區間[-1,1]，但我們不需要擴展的限定。對於相對於x的導數，我們容易導出以下關係第一種切比雪夫多項式的限定還允許通過x＝cos(t)的代換在連續情況中的正交關係的直接導出，即利用該正交關係，可以在區間x∈[-1,1]上建立在第一種切比雪夫多項式方面的函數的展開，即其中展開係數得到為其中已假設積分和求和的順序例如因為均勻的收斂而可以互換並且其中是諾依曼符號(Neumannsymbol)。諾依曼符號的存在激發了幾位作者引入Σ'記法，即為了以後方便，將在區間[-1,1]上的在第一種切比雪夫多項式方面的指數函數的展開給出為其中In(q)是階數n且自變數q的第一種修正貝塞爾函數。該展開從用於第一種貝塞爾函數和切比雪夫多項式與餘弦之間的關係的生成函數得出[5]。除了多項式之間的上面的連續正交性質，在多項式之間還有離散正交性質。接著在所謂切比雪夫節點處對切比雪夫多項式進行採樣，該所謂切比雪夫節點可以以兩種不同方式來限定：閉合規則和開放規則。閉合的切比雪夫節點被限定為多項式(1-x2)T′N(x)的N+1個零，其中單引號指示出相對於x的導數，即在該情況中，切比雪夫節點包括限定的域的邊界，即±1。這些切比雪夫節點可以被採用作為在切比雪夫高斯-羅巴託求積規則(ChebyshevGauss-Lobattoquadraturerules)中的橫坐標或樣本點。鑑於包含域的端點，這些規則被稱為「閉合求積規則」，參見[1]和[4，第106至112頁]。這些節點引出了離散正交關係針對m,n≤N，其中由於我們將對每個切片應用切比雪夫展開並且由於我們已經具有一種憑藉在各切片的頂部和底部採樣的場值使來自各個切片的響應耦合的機制，所以我們的關注點在於閉合規則、即包括區間[-1,1]的端點的切比雪夫節點的應用，並且我們將假設使用對應於閉合規則的節點。在該部分的末尾，針對所謂「開放規則」的情況給出了簡要概述。離散正交關係可以用於基於在切比雪夫節點的樣本f(xk)來構造f(x)的N階函數插值，即其中由於在切比雪夫節點的插值性質。針對上面的閉合規則的正交關係的展開產生因此展開係數可以被確定為後一公式可以解釋為I型離散餘弦變換(DCT-I)。該解釋非常重要，因為DCT在作用於含有針對k＝0,...,N的採樣的函數值f(xk)的長度N+1的數量上的DCT的一個應用上都產生針對n＝0,...,N的展開係數此外，DCT由於其與快速傅立葉變換(FFT)的關係因此是針對恰當選出的N的值的O(NlogN)的低複雜性算法。事實上，長度N+1的DCT-I精確地等效於(高達2的整體比例因子)具有偶對稱的2N個實數的FFT。結果，2N必須具有在小的素數上的因子分解以便產生有效算法。DCT-I例如已在軟體包FFTW中被實施。值得一提的是，I型DCT是其自己的逆向的按比例縮放的版本。這意味著樣本點值f(xk)可以憑藉DCT-I從展開係數再生。在利用切比雪夫多項式求和中的乘法因子1/dn的存在在一些文獻中用雙引號表示，即在下面相對於開放切比雪夫節點給出一些評論。可以將開放切比雪夫節點限定為TN+1的N+1個零，其不包括域的端點，如其引出了正交關係針對m,n0時算法的準確度和穩定性會發生什麼。據觀察，當γ的實部增加時或者當γ具有非零實部並且平板的厚度增加時，收斂率依然是指數的但相關聯的線性系統的條件數迅速地增加，如圖16所示。當在模擬中使用體積分方法考慮到的衰逝模式的數量增加時，迭代求解器需要許多迭代來收斂，即使針對相對低的對比。當模式的數量更進一步增加時，迭代求解器不能收斂。這些成果清楚地指示出歸因於所提出的算法的病態性(ill-conditioning)，因為之前對於使用分段線性展開時的同樣的低對比情況從來沒有發生過這樣的迭代收斂問題。此外，存在著如下理論結果：其表明包括分段線性展開和由切比雪夫多項式進行的展開在內的一般插值方法產生了具有接近連續公式化的條件調節的條件調節的積分方程，該連續公式化典型地被恰當地條件調節用於這裡所討論的種類的積分方程。因此插值自身不會引起病態性。結果，核的展開必須以某種方式負責，這與使核指數形式地迅速增加和衰變的擔憂相一致。解析積分算法在[2]中所提出的手段的最吸引人的性質在於，相對於格林函數的矩陣-矢量乘積由於DCT的應用和呈所謂左和右光譜積分矩陣[2]形式的隨後矩陣-矢量運算的稀疏性而具有低的計算成本。乍一看，不清楚這樣的性質是否可以通過訴諸將切比雪夫多項式和格林函數的乘積積分的另一手段來保持，因為矩陣-矢量乘積的結構取決於[2]中所提出的核展開。然而，為了洞察到在前述部分中指出的不穩定性的根源，我們將通過導出精確積分過程來繼續並且同時我們將表明所得的算法仍然是低複雜性的。類比於方程(1)，我們將未知的電流密度在次數M的一般多項式PM(z)方面展開並且考慮不定積分∫PM(z)exp(γz)dz＝QM(z)exp(γz),(28)其中Qm(z)再次是次數m的多項式。公式通過重複的部分積分得到。從計算點的角度看，關鍵點是使Qm(z)的係數與Pm(z)的係數相關，並且具有在z的值的範圍上的多項式Pm(z)和Qm(z)的迅速評估。多項式Pm和Qm的迅速評估可以通過將多項式寫入作為切比雪夫多項式的總和並且同時將z的值限制為如與在上面關於切比雪夫多項式的初步討論所指示出的呈DCT形式的下面的求積規則的橫坐標中的那些而得到。為了能夠應用切比雪夫多項式的性質，重點是首先通過引入下面的縮放比例將所感興趣的區間、即z∈[a,b]按比例縮放至t∈[-1,1]我們通過將按比例縮放的多項式Pm和Qm在切比雪夫多項式方面展開並且我們將方程(28)重寫為其中我們想要找到作為q和αn、n∈{0,...,M}的函數的所有βm。所需求的關係可以通過將上面的方程相對於t進行微分來找到，即因此我們具有多項式方程通過應用關係(2)並且隨後相對於t進行積分，我們獲得了其中C表示歸因於不定積分的積分常數。注意，用於T0(t)的係數歸於積分常數C而不能確定並且因此T0(t)已從上面的方程中去除。通過將係數與相等的切比雪夫多項式組成組，我們獲得了線性方程的集合這些線性關係可以在矩陣方程方面被總結為其中和上面的矩陣方程產生了在矩陣UM和DM兩者都高度稀疏並因此求解線性方程的集合的相關複雜性至少在原理上會是低複雜性、即O(N)的意義上的在矢量αM與βM的係數之間的適當的關係。乍一看，求解線性系統由於UM是上三角形矩陣而通過執行往回代換非常簡單地完成。不幸的是，矩陣是UM極端病態的並且結果在矢量βM中的所得係數歸因於四捨五入而極端不可靠。進一步的調查顯示，UM的病態性是歸因於可以變得任意小的單個奇異值。病態性也許用簡單的解析示例更好地來說明：該示例清楚地表明了用於使多項式階數減小的係數的幅值的極端增加。因此如果解析結果表明該類型的爆發(blow-up)，則矩陣UM必須是固有病態的，因為係數的生長由UM的逆向的範數界定。另一方面，如果如在數個數值測試中所觀察到的，病態性僅與單個奇異矢量相關，那麼應該可以將線性系統(40)分裂成恰當條件調節的系統和少量病態性的系統。就本身而言，系統的病態性部分仍然可以引出數值不穩定性，但如果能夠顯示總解的該分量並不顯著地為針對整體積分方程的最終解做出貢獻，那麼仍然存在有用於積分方程的穩定、恰當條件調節並且有效的數值算法的希望。為了表明病態性的根源，我們將方程(40)中的系統的第一列和最後一行分開並且我們將系統重寫為其中BR是由UM通過去除第一列和最後一行而得到，DR是由DM通過去除最後一行而得到，並且βR是由βM通過去除第一行、即取出β0而得到。數值測試顯示BR是恰當條件調節的矩陣並因此我們可以假設可以以穩定的方式計算出。注意，BR是三對角矩陣並因此計算BR的LU分解是O(N)運算並且在LU矩陣上的隨後的前向和後向代換由於這些矩陣是雙對角的事實也是O(N)的。因此計算對於形式BRx＝y的方程的解在複雜性上是O(N)的。上面的系統在逆向方面的解通過如下方程給出其中ek是第k個單位矢量、即除了在第k個條目以外到處都具有零的矢量。現在通過使用範數估計和與DR是具有小範數的線性算子的觀察可以容易地看出，上面的幅值β0必須對數值計算中的不穩定性負責。事實上，內積在M>>1時變得極小。與β0的大幅值對應的矢量是並且矢量自身由於BR的條件調節而可以被可靠地計算出。讓我們現在在區間[-1,t]上以及-1<tq的時修正貝塞爾函數的指數衰變顯示λ可以變得相當大，所以需要小心地進行數值實施。γM+1的限定在方程的集合中引入了一個額外的自由度、即γM+1，因為方程(56)中的λ與γM+1之間的連接事實上是系統方程(53)的最後一個方程。通過在方程(53)中替代關係(55)和(56)，我們獲得了對於γM+1成立的線性系統其中原始系統的最後一個方程由於方程(56)已被去除，並且該方程由針對方程(51)中的貝塞爾函數的遞推關係得出。線性系統(57)是針對M+2未知數的M+1方程的集合、即γ0,...,γM+1。結果，存在有固定確定未知數中的一個的自由。雖然在[5]中給出了對此的建議，其中較小矩陣需要以更複雜的簿記(bookkeeping)為代價被LU因子分解，但通過前述部分激發了我們的選擇並且我們將設定γ0＝0,(59)這實質上將右手側上的矩陣的第一列去除。針對γM+1的所得系統於是是這密切地類似於前述部分中的正則化系統。如此得到的矩陣方程已發現對於q的大範圍的真實和複雜值被恰當地條件調節，除了q非常接近零之外。後一情況可以通過將方程的整個集合乘以q來處理。此外，方程(60)中的線性系統的解由於矩陣A(-q)的三對角本質而有效地得到，該矩陣A(-q)利用有效前向和後向代換算法產生了雙對角LU因子，如例如LAPACK(線性代數包)中實施的。避免減去求和中的消去我們現在回到在區間[-1,t]上的原始積分並且在γM+1方面具有-1<t|q|就展現出作為M的函數的指數生長。為了進一步調查因子FA(-q,t)，我們回到方程(16)。針對在切比雪夫多項式方面的指數函數的該表示可以用於導出針對FA(t)的可替表示達，還參見[5]，對於FA(-q,t)的後一表示，我們現在包括1/IM+1(-q)，即由於序列Im(q)典型地是指數衰變序列，所以我們可以預料級數收斂非常快並且我們注意到序列的第一項的幅值由一界定。結果，作為M的函數的1/IM+1(-q)的指數增加憑藉該表示被成功地抑制。與[5]相對，我們對於FA(-q,t)總是使用後一表示，因為我們已得出經驗它總是穩定的。缺點是該貢獻必須被預先計算出而前一表示容易被包括在其他求和中。剩下的任務現在是對於t的給定值實際地計算出上面的表示(63)的級數，即做到這一點的有效方式是採用Clenshaw遞推公式[3，第172至177頁]。雖然貝塞爾函數和切比雪夫多項式兩者可以被選擇為用於遞推的基，但我們採用了在Clenshaw算法中的用於切比雪夫多項式的遞推，而貝塞爾函數的比率已在早期步驟中基於方程式(51)的後向遞推關係、即米勒算法被生成為其中針對N的RN(z)＝0的起始值比在求和中考慮到的修正貝塞爾函數的最大階數大至少20倍。為了獲得求和所需的比率，即對於m≥M+1的Im(-q)/IM+1(-q)，我們注意到這些比率可以通過使比率Rm(z)以遞歸的方式相乘而得到，即積分的採樣在整個過程中的最終步驟是將來自電流密度的展開係數的映射引入離散變量的新集合。這是能夠構造有限線性系統、即在(1)中的考慮下的用於積分的矩陣-矢量乘積所需要的。基本上，有可以遵循的兩個手段。第一個是將整個積分近似為僅切比雪夫多項式的總和，這意味著(61)中的三項中的兩個需要在切比雪夫多項式方面進行近似，即本質上是exp[-q(1+t)]和FA(-q,t)。第二手段是在規定點tk對積分採樣，使得可以獲得切比雪夫多項式的總和的有效計算。由於我們不妨將切比雪夫展開與已經在體積分方法中起作用的空間採樣手段合併，所以可以方便地選擇第二手段、即對積分採樣。針對採樣點tk的選擇應該由離散餘下變換的應用得到，因為這是用以同時評估在樣本範圍上的切比雪夫多項式的加權和的最有效的方式。這留下兩個可能性：開放原則或閉合原則，如第2部分中說明的。從前述討論可以容易地看出，端點t＝±1也存在於求和中，這意味著閉合規則是最方便的選擇。閉合原則與DCT-I一致，如方程(23)中，並且樣本點通過方程(17)給出，即FFTW中的DCT-I的精確限定和實施由如下方程給出其中DCTI[f(tk)](m)是f(tk)的DCT-I的第m個元素，並且dk已在方程(19)中被限定為在整體算法中，現在有要求DCT-I的兩個步驟。第一個是當方程(31)中的展開係數αm必須由對比電流密度ji(z)的在切比雪夫節點處的採樣值確定時。通過限定，我們假設我們具有展開其中和從方程(22)中的關係我們具有並因此這意味著係數DCTI[j(zk)](M)必須乘以1/2。要求DCT-I的第二步驟是當方程(1)中的積分G1(z)和G2(z)的切比雪夫展開的係數gm已計算出並且展開需要在切比雪夫節點zk處被評估時，即其中全矩陣-矢量乘積現在讓我們回到在(1)中限定的原始積分G1(z)和G2(z)並且總結至此所採取的步驟。計算由需要執行一次的準備階段和可能作為矩陣-矢量乘積執行許多次的執行階段組成。準備階段由下面的步驟組成:1.將區間[a,b]按比例縮放至[-1,1]並且將γm按比例縮放至q，如在方程(4)中。2.選擇切比雪夫展開的最大階數：M。3.將長度M+1的DCT-I初始化。4.如方程(17)中計算針對閉合原則的切比雪夫節點：tk。5.在方程(60)中計算三對角矩陣A(-q)的元素。6.使用LAPACK計算A(-q)的LU因子分解。7.如5.1部分中說明的使用Clenshaw算法在方程(63)中計算函數F(k)＝FA(-q,tk)/IM+1(-q)。8.計算函數v1(k)＝exp[-q(1+tk)]和v2(k)＝exp[-q(1-tk)]這裡需要注意的是，對於積分G2，需要矩陣A(q)，但是我們可以為此利用A(-q)的LU分解，因為A(q)＝-A(-q)T。類似地，對於G2我們需要A(q,tk)/IM+1(q)＝FA(-q,-tk)/IM+1(-q)＝F(M-k)並且v1(k)和v2(k)的角色互換，因為在節點處的反對稱性tk＝-tM-k。執行階段由下面的步驟組成：1.憑藉DCT-I如方程(76)中計算電流密度的展開係數αm。2.利用方程(42)中限定的DM計算DMαM。3.使用A(-q)的預先計算的LU因子，計算矢量和的係數作為方程(60)的解，即A(-q)γ1＝DMαM,(79)A(q)γ2＝DMαM,(80)4.限定和5.計算和6.計算7.計算由在矢量j中組織的電流密度的樣本生成G1(k)和G2(k)的兩個矩陣-矢量乘積可以被緊湊地寫作線性運算的序列。為了使記法容易，引入四個附加線性算子，例如對於任意矢量p＝(p0,...,pM)T我們限定CMp＝DCTI[pm],(81)SMp＝(0,p0,...,pM-2,2pM-1)T,(83)PMp＝pM,(84)P0p＝p0,(85)即，CM現在表示I型DCT，NM是對角歸一化矩陣，SM是與乘法組合的移位矩陣，並且PM是篩出矢量的最後條目的投影算子。SM的矩陣表示通過式(86)給出和P0與PM的矩陣是P0＝(1,0,…,0)PM＝(0,…,0,1)(87)利用這些限定，我們可以將針對G1＝(G1(0),...,G1(M))T和G2＝(G2(0),...,G2(M))T的矩陣-矢量乘積表達為其中我們已引入了識別算子IM和矢量F1＝(F(0),...,F(M))T與F2＝(F(M),...,F(0))T。伴隨矩陣-矢量乘積在前述部分中所引入的線性算子的幫助下，可以容易地構造出兩個矩陣-矢量乘積的伴隨。在正式意義上，線性運算的順序需要逆向並且各算子必須用其伴隨替換。起始於方程(88)中的用於G1的表示並且用上標H表示伴隨，我們獲得了其中後一等式是IM和NM的自伴隨和矩陣CM、DM、SM、P0、PM是實值並因此它們的伴隨等於它們的移項的觀察的結果。各個矩陣的伴隨或移項中的所有都容易建立和編程。唯一更多牽涉到的伴隨是A-H(-q)的，但是這可以憑藉採用A(-q)的LU因子分解(憑藉zgttrf得到)的LAPACK例程zgttrs來執行，並因此相應的矩陣-矢量乘積可憑藉該例程是得到。最後，方程(89)中用於G2的表示的伴隨產生注意，矩陣A-H(q)＝-A-H(-q)並因此與LAPACK例程zgttrs組合的A(-q)的LU分解可以被用於執行伴隨矩陣-矢量乘積的該部分。連接多個切片切比雪夫展開最好在方程(1)中的對比電流密度jm(z)的所有分量都可連續地微分至非常高的階數時工作。在這種情況下，插值估計顯示出切比雪夫展開的近似上的誤差隨著多項式的線性增加的階數而成指數減小。然而，對比電流密度的可微性取決於光柵的幾何結構及其材料成分。當材料成分在縱向、非周期性坐標z的某值處急劇改變時或者當光柵的幾何結構展現出扭結或間斷時，對比電流密度潛在地不連續或者具有不連續的一階導數。在間斷或不連續導數的情況中的切比雪夫展開的差的收斂可以通過使用於對比-電流密度的展開的區間分裂成較小子區間或者切片來減輕，使得對比-電流密度在各切片的內部上可連續地微分至高階。假如我們預料到在z＝a1處的間斷，那麼將區間[a,b]分區成切片[a,a1]和[a1,b]。於是在各切片上限定了用於對比-電流密度的單獨的切比雪夫展開，並且如方程(1)中給出的將對比-電流密度與格林函數一起積分的以前描述的方法可以在每個切片上執行。備選地，可以選擇在一個子區間上採用切比雪夫展開並且在另一子區間上採用另一類型的展開、例如分段展開。還有，在這樣的情況中，可以在每個切片上採用已經文檔記錄的積分方法並且有待回答的唯一問題是如何將貢獻從一個切片耦合至另一個。為了回答該問題，我們將注意力集中在方程(1)中的積分G1(z)上，因為手段對於G2(z)類似。對於兩個切片、即區間[a,a1]和[a1,b]的情況，我們有以下兩種情況要考慮：觀察坐標z處於區間[a,a1]中或區間(a1,b]中。前一情況在兩個切片之間不產生耦合，因為積分的區間起始於z＝a並因此該情況可以通過用於一個切片的積分的原始方法來處理。對於情況z∈(a1,b]，我們將積分G1(z)重寫為上面的最終表達顯示兩個切片之間的耦合採取指數函數乘已經從跨越切片[a,a1]的積分得到的已經計算出的常數G1(a1)的形式。第二積分是跨越單個切片的標準積分，這在以前已經進行了討論。因此兩個或多個切片之間的耦合是簡單地添加演變作為觀察點z乘從以前的切片的端點已經計算出的貢獻的指數函數的額外項。當在切片[a1,b]上使用切比雪夫展開時，那麼已經在以第7部分中限定的矢量v1(k)的形式計算出的上面的結果中的所要求的指數函數和來自切片[a,a1]的附加貢獻可以容易地與全矩陣-矢量乘積的執行階段的在步驟6中的常數H1(0)合併，以達到在浮動點運算的數量上的最大效率。在上面描述的實施例中，切比雪夫展開已被用作用於在計算電磁散射性質的體積分方法中所使用的對比電流密度的展開的沿著縱向非周期性(z)方向的分段線性展開的可替代方案。對於數值穩定性，正則化步驟可以用於計算格林函數與對比電流密度的切比雪夫展開的相互作用。所得的算法在數值上穩定並且有效、即O(NlogN)，其中N是沿著z的樣本點的數量。數值測試顯示，在體積分方法中的切比雪夫展開展現出反射係數的指數收斂。作為結果，當與體積分方法中的分段線性展開相比時，尤其是當在分段線性展開的情況中每個切片的樣本的數量大時，切比雪夫展開是有競爭力的並且經常在計算時間方面更快。這是當切片相對於(局部)波長厚時發生。需要許多分段線性樣本的另一情況是當橫向方向上的傅立葉模式的數量高時。第二個效果在於，當需要較少樣本時體積分方法的存儲器要求將會降低。也可以與現有的分段線性展開並排地、和/或與具有不同係數的切比雪夫展開並排地、和/或與勒讓德展開並排地實施切比雪夫展開，以這樣的方式使得可以對各切片單獨地進行針對特定的展開的選擇。這允許了使用不同的展開。例如，分段線性展開對於具有非常少的樣本的薄切片最適宜，而切比雪夫展開在切片厚時最有效。在切比雪夫展開的情況中的針對每個切片的樣本數量的選擇應該反映出DCT在其相應的FFT的長度可因子分解成小素數、即典型地2、3和5時最有效。圖17A和圖17B是根據本發明的實施例的方法的流程圖。圖17A和圖17B的步驟可以用如分別在圖11、圖13和圖15中的1150(步驟1116至1120)、1350(步驟1116至1120)和1550(步驟1506至1510)那樣用虛線方框識別出的步驟取代。這些步驟在更一般情況下如分別在圖12和圖14中的1250和1450那樣用虛線方框識別出。實施例是計算結構的電磁散射性質的方法，結構包括不同性質的材料並且結構在至少一個橫向方向上是周期性的並且在相對於至少一個橫向方向正交的方向、在該示例中是z方向上延伸。方法牽涉到：通過針對在至少一個橫向方向上的多個模式中的每個相應模式執行在正交方向上的偽譜(在該示例中是切比雪夫)多項式展開乘以對於多個模式所有模式都使用正交方向上的相同樣本點的1D格林函數的積分，針對多個模式在數值上求解用於電磁散射的體積分方程，其中積分通過求解方程的正則化線性系統來執行。圖17A和圖17B中的步驟是：在步驟1702中，設定特定用於各模式的展開。在步驟1704中，通過如下方法正則化：生成包括易於發生與條件調節相關的誤差的係數的在z上的樣本點(切比雪夫降低)處的函數F(k)，並且通過限定正則化的向上/向下展開係數矢量γ1＝(γ11..γ1M,γ1M+1)和γ2＝(γ21..γ2M,γ2M+1)修改線性系統以補償F(k)。因此方程的線性系統通過藉助限定擴展的正則化展開係數矢量(γ1,γ2)修改線性系統以補償易於發生與條件調節相關的誤差的展開係數而被正則化。在該示例中的術語「擴展的」包括添加行至矢量並去除矢量的第一條目。本領域技術人員將領會的是擴展是在正則化方案的情況下完成，並且它是意味著通過擴展進行的信息的引入或在解中保持信息的能力。可選地，將方程的線性系統正則化的步驟可以包括生成在正交方向上的樣本點處的函數(F(k))，函數包括易於發生與條件調節相關的誤差的展開係數，使得線性系統的修改補償函數(F(k))。可選地，在正交方向上的樣本點處的函數(F(k))的生成使用遞推公式。在步驟1706中，使用在z上的樣本點(切比雪夫節點)處的電流密度(m1,m2,z)的採樣值的離散變換(當使用切比雪夫展開時是DCT)來計算(切比雪夫)展開係數矢量αM。在步驟1708中，使用(切比雪夫)展開係數矢量來αM計算光譜差異化的對比電流密度矢量DMαM。在步驟1710中，通過向上/向下求解橫跨z域的方程的正則化線性系統以計算出正則化展開係數矢量γ1和γ2來執行針對對比電流密度乘1D格林函數的向上/向下組分(對應於A(-q)和A(q))的(切比雪夫)展開的積分。因此方程的正則化線性系統在第一與第二離散變換步驟之間求解以計算出正則化展開係數矢量(γ1,γ2)的值。在步驟1712中，從計算出的正則化展開係數矢量γ1和γ2中分離出不同部分。1714和1716示出不同部分。在1714中，示出了非擴展的向上和向下部分和在實踐中，這些部分的分離可以通過複製儲存了矢量γ1和γ2的陣列並修改陣列來完成。在該示例中，各陣列的最後條目被去除並且被複製到用於步驟1716的存儲中並且第一條目被設為零。雖然這裡選擇了零，但可以使用其他值。可以插入額外的條目以便使矢量具有用於矩陣乘法的正確長度。在1716中，示出了向上和向下計算出的條目γ1M+1和γ2M+1。在未使用F(k)的實施例中，這些條目可以被丟棄(並且甚至不分離出)。在步驟1718中，使用正則化展開係數矢量γ1和γ2的非擴展向上和向下部分和的第二離散變換(當使用切比雪夫展開時是DCT)來計算在z上的樣本點處的正則化積分H1(k)和H2(k)。因此第二離散變換步驟被應用於正則化展開係數矢量(γ1,γ2)的非擴展部分以計算出在正交方向上的樣本點處的正則化積分(H1(k)、H2(k))。在未使用F(k)並且條目γ1M+1和γ2M+1被丟棄的實施例中，在該階段可以執行正則化積分H1(k)和H2(k)的線性組合以計算出在沒有反射時的在z域中的散射電磁場該結果等效於如分別在圖11、圖13和圖15中的1150、1350和1550所識別出的步驟的結果。因此通過將圖17A和圖17B的以上步驟插入如參照圖11至圖15所描述的體積分方法內，可以使用數值求解的結果、在該示例中使用計算出的正則化積分(H1(k)和H2(k))來計算出結構的電磁散射性質。在使用F(k)並且條目γ1M+1和γ2M+1未丟棄的實施例中，代替正則化積分H1(k)和H2(k)的線性組合，步驟1720和1722可以被用於進一步改進性能。在步驟1720中，將正則化積分H1(k)和H2(k)與條目γ1M+1和γ2M+1乘以包括易於發生與條件調節相關的誤差的係數的函數F(k)組合以計算出在z上的樣本點處的最終積分G1(k)和G2(k)。因此方法可以在離散變換步驟之後進一步包括將正則化積分(H1(k)和H2(k))與正則化展開係數矢量(γ1,γ2)的擴展部分(γ1M+1,γ2M+1)乘以函數(F(k))組合以計算出在正交方向上的樣本點處的進一步的積分(G1(k)和G2(k))的步驟。在步驟1722中，執行最終積分G1(k)和G2(k)的線性組合以計算出在沒有反射時的在z域中的散射電磁場該結果等效於如分別在圖11、13和15中的1150、1350和1550所識別出的步驟的結果。通過將包括步驟1720和1722的圖17A和圖17B的以上步驟插入如參照圖11至圖15所描述的體積分方法內，可以使用計算出的進一步的積分來計算出結構的電磁散射性質。在參照圖17A和圖17B所描述的實施例中，偽譜多項式展開是切比雪夫展開、離散變換是離散餘弦變換並且在正交方向上的樣本點是切比雪夫節點。此外，切比雪夫節點包括積分被執行所跨越的在正交方向上的域的端點。切比雪夫展開具有在特定柵格上的樣本與DCT之間的關係，因此可以使用FFT有效地實施。在另一實施例中，偽譜多項式展開是勒讓德展開並且離散變換是離散勒讓德變換。具有正則化的所提出的偽譜多項式展開產生較短的計算時間並且要求用於在波長方面高的光柵的較少存儲器。對於高達大約0.2波長高的光柵，計算時間上的增益相對低，即2的因子，但是對於具有數個波長的高度的光柵、例如在用於極紫外(EUV)光刻的量測中所使用的光柵來說，可以獲得在計算時間上的15至20的因子的改進。關於存儲器，增益直接與所要求的樣本的數量成正比，即已觀察到從8的因子到超過20的因子的內側節省。此外，這裡所描述的實施例在光柵的特定的部分(例如薄層)可以用低階展開被展開並且在波長方面長的其他部分以偽譜多項式展開被展開的意義上可以與已經現有的低階展開(例如分段線性)組合。這產生了利用各展開的強項的整體算法。圖18以示意性形式示出配置有為了執行根據本發明的實施例的方法的程序和數據的計算機系統。計算機系統包括中央處理單元(CPU)1802和用於存儲在程序執行期間的程序指令1806和數據1808的隨機存取存儲器(RAM)1804。計算機系統還包括用於存儲在程序執行之前和之後的程序指令和數據的盤存儲1810。程序指令1806包括離散餘弦變換(DCT)例程1812、矩陣乘法函數1814、諸如加法和減法1816和陣列組織函數1818等的其他算數函數。數據1808包括在VIM系統的解的計算期間使用的4D陣列1820和2D陣列1822。用於輸入和輸出的其他傳統計算機部件未示出。在本發明的實施例中，傅立葉級數展開可以通過採用完美匹配層(PML)或者用以模仿朝向無限接近在其上使用傅立葉展開的單位單元的邊界的輻射的其他類型的吸收邊界條件而用於解析非周期性結構。本發明的實施例可以根據參照圖5和圖6所描述的重構方法來實施以提供從由通過輻射照射對象而產生的檢測到的電磁散射性質重構對象的近似結構的方法。本發明的實施例可以通過在參照圖3和圖4所描述的處理單元PU上實施這裡所描述的方法以提供用於重構對象的近似結構的檢查設備來實施。參照圖3、圖4和圖18所描述的處理器可以在含有用於計算結構的電磁散射性質的計算機可讀指令的一個或多個序列的電腦程式的控制下操作，指令適於引起一個或多個處理器執行這裡所描述的方法。雖然可能在該正文中對IC的製造中的檢查設備的使用進行了特定參考，但應該理解的是，這裡所描述的檢查設備可以具有其他應用，如集成光學系統的製造、用於磁疇存儲器、平板顯示器、液晶顯示器(LCD)、薄膜磁頭等的引導和檢測圖案。本領域技術人員將領會的是，在這樣的可替代應用的情況下，本文中的術語「晶片」或「裸片」的任何使用可以被視作分別與更上位的術語「襯底」或「目標部分」同義。這裡提到的襯底可以在曝光之前或之後在例如軌道(典型地將一層抗蝕劑施加至襯底並使經過曝光的抗蝕劑顯影的工具)、量測工具和/或檢查工具中進行處理。在適用時，本文中的公開可以應用於這樣的和其他襯底處理工具。此外，襯底可以被處理超過一次，例如以便創建多層IC，使得這裡所使用的術語襯底也可以是指已經含有多個經過處理的層的襯底。上面描述的根據本發明的實施例的方法可以被包含到前向衍射模型內，用於從由通過輻射照射對象而產生的諸如衍射圖案等的檢測到的電磁散射性質來重構對象(不限於1D周期性的)的近似結構，如上面參照圖5和圖6所描述的。上面參照圖3和圖4所描述的處理單元PU可以被配置成使用該方法來重構對象的近似結構。雖然可能已在上面對在光學光刻的情況下的發明的實施例的使用進行了特定參考，但應該領會的是，發明可以在任何應用、例如壓印光刻中使用，並且只要情況允許並不限於光學光刻。在壓印光刻中，圖案形成裝置中的拓撲限定了創建在襯底上的圖案。可以將圖案形成裝置的拓撲按壓到供給至襯底的一層抗蝕劑內，隨之通過施加電磁輻射、熱、壓力或其組合使抗蝕劑固化。在抗蝕劑固化之後，將圖案形成裝置從抗蝕劑上移走，在其中留下圖案。這裡所使用的術語「輻射」和「光束」涵蓋所有類型的電磁輻射，包括紫外(UV)輻射(例如，具有或大約365nm、355nm、248nm、193nm、157nm或126nm的波長)和極紫外(EUV)輻射(例如，具有在5nm至20nm的範圍內的波長)，以及諸如粒子束或電子束等的粒子束。術語「透鏡」只要情況允許可以是指包括折射型、反射型、磁性型、電磁型和靜電型光學部件在內的各種類型的光學部件中的任一個或組合。術語「電磁」涵蓋電的和磁的。術語「電磁散射性質」涵蓋反射和透射係數及散射測量參數，包括光譜(如作為波長的函數的強度)、衍射圖案(作為位置/角度的函數的強度)和橫向磁的與橫向電的偏振光的相對強度和/或在橫向磁的與橫向電的偏振光之間的相位差。衍射圖案自身可以例如使用反射係數進行計算。因此，雖然關於反射散射描述了本發明的實施例，但發明也適用於透射散射。術語「正則化」是指引入附加信息以便解決不適定問題(ill-posedproblem)或防止過度擬合的過程。雖然已在上面描述的發明的特定實施例，但應該領會的是，發明可以以除了所描述的以外的方式實踐。例如，發明可以採取含有描述了如上面所公開的方法的計算機可讀指令的一個或多個序列的電腦程式或者其中存儲有這樣的電腦程式的數據存儲介質(例如，半導體存儲器、磁或光碟)的形式。需要領會的是，詳細描述部分並且不是發明內容和摘要部分意在用於解釋權利要求。發明內容和摘要部分可以陳述如發明人所設想出來的本發明的一個或多個但不是所有示例性實施例，並因此不意在以任何方式限制本發明和隨附權利要求。上面已在圖示出指定功能及其關係的實施的功能構造塊的幫助下描述了本發明。這些功能構造塊的界限為了描述方便在這裡被任意進行了限定。可以限定可替代的界限，只要指定功能及其關係被適當地執行。特定實施例的上述描述如此充分地揭示了發明的一般性質以至於其他人可以通過應用本領域技術內的知識容易地在無需過度實驗的情況下為各種應用修改和/或改寫這樣的特定實施例，而不會脫離本發明的一般概念。因此，這樣的改寫或修改意在落入基於這裡所呈現出的教導和指導的所公開的實施例的等效方式的含義和範圍內。需要理解的是，本文中的措辭或術語是為了描述的目的並且不是限制性的，使得本說明書的術語或措辭應當由技術人員根據教導和指導來解釋。本發明的寬度和範圍不應該受上面描述的示例性實施例中的任一個限制，而是應該根據下面的權利要求及其等效方式來限定。參考文獻[1]L.M.Delves和J.L.Mohamed，積分方程的計算方法，劍橋大學出版社，1985年。[2]S.-Y.Kang、I.Koltracht和G.Rawitscher，具有間斷核的積分方程的-Clenshaw-Curtis求積法，計算數學，72:729–756，2002年3月。[3]W.H.Press、S.A.Teukolsky、W.T.Vetterling和B.P.Flannery，Fortran77中的數值選配方案：科學計算領域，劍橋大學出版社，第二版，1992年。[4]A.Quarteroni和A.Valli，偏微分方程的數值近似，斯普林格計算數學系列，斯普林格，1994年。[5]T.Hasegawa和T.Torii，通過切比雪夫級數展開的振蕩函數的不定積分，計算與應用數學學報，17:21–29，1987年。