一種基於時空動態耦合的三維溫度傳感數據分析方法與流程
2023-06-05 05:03:21 5
本發明提供一種三維溫度場的動態數據分析方法,具體涉及一種基於時空動態耦合的三維溫度傳感數據分析方法,屬於工業工程領域。
背景技術:
溫度場的動態數據分析技術在工程領域發揮著重要作用,對提高產品質量、提升系統性能等工程任務提供重要信息。近年來,這項技術引起科研與工程人員的廣泛關注,已經在生態、氣象、衛生保健、糧食倉儲等工程領域得到應用。溫度場的動態數據分析技術能為複雜系統的監控提供全面、準確的信息,達到提高系統性能或服務質量的效果。同時,該技術有助於工程結構的優化設計,實現節約資源、降低成本的目標。
溫度場的動態數據分析技術旨在實現對溫度場的準確估計。傳統的溫度場估計方法是一種基於熱傳遞原理的仿真方法。文獻[1]~[2]中記載,該方法考慮影響溫度場的變化的外部因素,如環境因素、內部傳熱機制,通過給定初始溫度和邊界條件,建立三維熱力學模型,實現對三維動態溫度場的估計。然而,溫度場的變化不僅受到外部因素的影響,還受到內部因素及其他多種不確定因素的影響。溫度場可以被視為一個隨著時空變化的複雜的傳熱系統。傳統的溫度場估計方法僅能刻畫在理想狀態下溫度場變化的輪廓和趨勢。對於溫度場中經常出現的由內部因素引起的局部溫度變化,該方法不再適用。因此,傳統的溫度場估計方法誤差較大,無法提供高精度的溫度場信息。
隨著時代的發展,無線傳感器技術被廣泛應用於工程領域(如文獻[3])。該技術通過無線傳感器採集溫度數據,並利用這些數據建立溫度場估計模型。由於傳感器配置成本的限制,目前在溫度場中安裝的傳感器數目較少,通過傳感器只能獲取一少部分稀疏的觀測數據。觀測數據的稀疏性會導致溫度場估計模型精確度大大降低。同時,由傳感器採集的溫度數據存在測量誤差,同樣會降低溫度場估計模型的精確度。因此,僅依靠無線傳感器技術與數學模型相結合的方法無法實現對溫度場的精準估計。
此外,作為一個複雜的傳熱系統,三維溫度場相鄰位置或相鄰時刻的溫度數據存在時間和空間的相關性,且溫度數據的時、空相關性是相互作用的,即數據間既存在時間相關性、空間相關性,又存在時空相關性。現有的研究對溫度場這一特性的描述多是在時間和空間相關性是相互獨立的假設條件下進行的,沒有考慮數據的時空相關性,難以實現對三維動態溫度場的時空相關性進行考量和估計。
參考文獻
[1]d.wangandx.zhang,「apredictionmethodforinteriortemperatureofgrainstorageviadynamicsmodel:asimulationstudy」,proceed-ingsofieeeinternationalconferenceofautomationscienceandengineering,pp.1477-1483,2015.
[2]c.jia,d.sunandc.cao,「finiteelementpredictionoftransienttemperaturedistributioninagrainstoragebin」,journalofagriculturalengineeringresearch,vol.76,no.4,pp.323–330,2000.
[3]y.ding,e.a.elsayed,s.kumara,j.lu,f.niuandj.shi,「distributedsensingforqualityandproductivityimprovements」,ieeetransactionsonautomationscienceandengineering,vol.3,no.4,pp.344–359,2006.
技術實現要素:
針對上述現有技術存在的不足,本發明提供一種基於時空動態耦合的三維溫度傳感數據分析方法,在混合效應模型的框架下,將反映傳熱機理的溫度場物理模型與基於時空相關性的統計模型相結合,實現對三維動態溫度場的估計。通過本發明能夠解決目前在工程領域中存在的由於傳感器數據不足無法獲得準確、全面溫度場信息的問題,可以得到溫度場的全面而準確的信息,為工程領域中監控、決策等措施提供依據。
本發明提供的技術方案如下:
一種基於時空動態耦合的三維溫度傳感數據分析方法,利用反映傳熱機理的溫度場物理模型與基於時空相關性的統計模型,建立混合效應模型,對三維溫度傳感數據進行分析,獲得三維空間位置上的動態溫度值(即任一空間位置或任一時刻溫度值);包括如下步驟:
1)利用溫度場物理模型與基於時空相關性的統計模型,建立混合效應模型框架,三維溫度場某時空點的溫度值包括表示溫度場的全局溫度變化的均值函數項、表示溫度場的局部溫度變化的局部變化項和表示由隨機或不可控因素引起的溫度變化的隨機噪聲項;
建立混合效應模型框架如下:
假設y(s,t)表示三維溫度場在時空點(s,t)的溫度值,s和t分別表示空間和時間的自變量,混合效應模型的框架為:
y(s,t)=μ(s,t)+w(s,t)+∈(s,t)(式1)
其中,μ(s,t)表示在時空點(s,t)處的均值函數項,用來刻畫溫度場的全局溫度變化情況;w(s,t)表示在時空點(s,t)處的局部變化項,用來刻畫溫度場的局部溫度變化情況;∈(s,t)表示在時空點(s,t)處的隨機噪聲項,用來刻畫由隨機或不可控因素引起的溫度變化情況,通常假設其為白噪聲。下面,將分別對均值函數項μ(s,t)和局部變化項w(s,t)建立模型。
2)均值函數項μ(s,t)的建模,實現方法為:
b1.建立均值模型:
溫度場的變化通常是由環境因素引起的。本發明中,充分考慮環境因素的影響,在笛卡爾坐標系下,對均值函數項μ(s,t)建立三維非穩態傅立葉傳熱模型:
式2中,μ(x,y,z,t)表示在笛卡爾坐標系下的均值函數項,其中空間坐標s={x,y,z},x、y和z分別表示在x、y和z方向的坐標;ρ表示物質的密度,c表示物質的比熱容,λx,λy和λz分別表示在三維笛卡爾坐標系下物質沿x,y和z方向的熱導率。
b2.均值模型的求解
採用有限差分法,利用式3對式2求解:
其中,(i,j,k,m)表示坐標(x,y,z,t)對應的網格位置,δx,δy,δz和δt分別表示空間、時間方向的網格間隔。為保證這種數值解法的精確度,參數值的選取應保證給定初始溫度及邊界條件,採用有限差分法即可實現對均值函數的求解。
3)局部變化項w(s,t)的建模,實現方法為:
充分考慮溫度場的時空相關性,採用高斯隨機場與克裡金模型相結合的方法來刻畫溫度場的局部溫度變化。
c1.採用高斯隨機場確定模型框架
假設在時刻tm(m=1,2,…,m),局部溫度變化具有空間平穩性,採用高斯隨機場模型描述si點的溫度與其相鄰位置溫度的關係,即在給定si點相鄰位置溫度值的條件下,si點的溫度與服從於正態分布:
其中,sj~si表示si和sj在高斯隨機場中處於相鄰位置,ωij(tm)表示在tm時刻的空間權重參數,σ2(si,tm)表示條件方差。
c2.採用克裡金模型確定權重參數
採用克裡金模型,通過式5確定權重參數ωij(tm):
其中,c(si,sj)表示si與sj的協方差矩陣,c(sj,sj)表示sj之間的協方差矩陣。協方差矩陣由協方差函數確定,協方差函數的表達式如式6:
其中sp和sq分別表示p和q點處的空間坐標,在笛卡爾坐標系下,sp={xp,yp,zp}和sq={xq,yq,zq};為在tm時刻下協方差函數的參數,將η={{η(t1),η(t2),…,{η(tm)}記為協方差參數。
c3.協方差參數求解
在初始時刻t1,採用極大似然估計方法求解協方差參數。為了刻畫溫度場的時間相關性,採用貝葉斯估計方法對t2到tm時刻的協方差參數進行更新。假設已知t1到tm-1時刻的協方差參數及溫度數據(m=2,…,m),通過式7得到tm時刻協方差參數的預測分布:
p(η(tm)|y(s,t1:m-1))=∫p(η(tm)|η(tm-1))p(η(tm-1)|y(s,t1:m-1))dη(tm)(式7)
其中,p(η(tm)|y(s,t1:m-1))表示在已知t1到tm-1時刻溫度數據y(s,t1:m-1)的條件下,tm時刻的協方差參數η(tm)的概率密度;p(η(tm)|η(tm-1))表示在已知tm-1時刻的協方差參數η(tm-1)的條件下,tm時刻的協方差參數η(tm)的概率密度;p(η(tm-1)|y(s,t1:m-1))表示在已知t1到tm-1時刻溫度數據y(s,t1:m-1)的條件下,tm-1時刻的協方差參數η(tm-1)的概率密度。
再通過式8,利用tm時刻的溫度數據實現協方差參數的更新,即求協方差參數的後驗概率密度分布p(η(tm)|y(s,t1:m)):
其中,
p(y(s,tm)|y(s,t1:m-1))=∫p(y(s,tm)|η(tm))p(η(tm)|y(s,t1:m-1))dη(tm)(式9)
p(y(s,tm)|η(tm))表示在tm時刻的協方差參數η(tm)的條件下,y(s,tm)的概率密度。由於參數的分布是非正態的,因此採用粒子濾波方法實現貝葉斯估計的迭代計算。
4)時空溫度場估計,實現方法為:
參數估計之後,給定觀測數據,通過式10實現對溫度場中任何位置的溫度值的估計:
其中,在tm時刻點的溫度估計值。
與現有技術相比,本發明的有益效果是:
本發明提供一種基於時空動態耦合的三維溫度傳感數據分析方法,利用反映傳熱機理的溫度場物理模型與基於時空相關性的統計模型,建立混合效應模型,對三維溫度傳感數據進行分析,獲得三維溫度場中任一空間位置的動態溫度值(即任一空間位置或任一時刻溫度值)。通過本發明所提供的技術方案,將反映傳熱機理的溫度場物理模型與基於時空相關性的統計模型相結合,建立混合效應模型,實現對三維動態溫度場的估計,為溫度場的實時監控提供準確、全面的信息,有助於實現溫度場中傳感器的最優配置,達到降低成本、節約能源的效果。
附圖說明
圖1是本發明提供的基於時空動態耦合的三維溫度傳感數據分析方法的流程框圖。
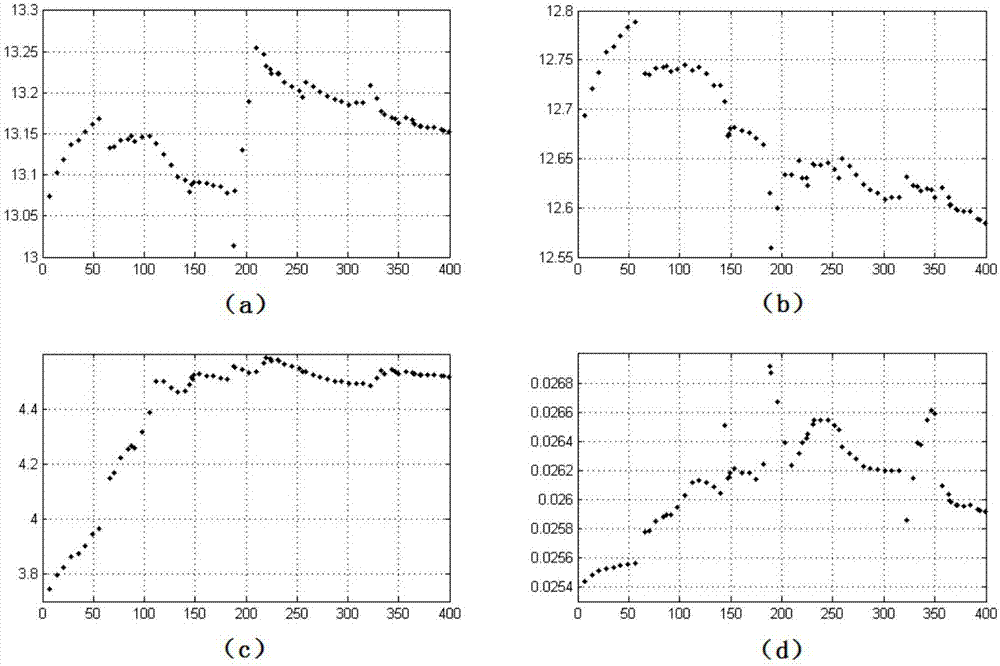
圖2是本發明實施例的協方差參數估計結果;
其中,橫坐標為時間,單位為天;縱坐標為協方差參數值;(a)為參數ax的估計值;(b)為參數ay的估計值;(c)為參數az的估計值;(d)為參數的估計值。
圖3是本發明實施例的糧食溫度場的估計結果;
其中,圖例中數字是採樣點的空間坐標。
具體實施方式
下面結合附圖,通過實施例進一步描述本發明,但不以任何方式限制本發明的範圍。
本發明提供一種基於時空動態耦合的三維溫度傳感數據分析方法,在混合效應模型的框架下,將反映傳熱機理的溫度場物理模型與基於時空相關性的統計模型相結合,實現對三維動態溫度場的估計。通過本發明能夠解決目前在工程領域中存在的由於傳感器數據不足無法獲得準確、全面溫度場信息的問題,可以得到溫度場的全面而準確的信息,為工程領域中監控、決策等措施提供依據。
圖1是本發明提供的基於時空動態耦合的三維溫度傳感數據分析方法的流程框圖。實施例設定溫度場範圍為(-50℃,50℃),利用傳感器採集溫度數據,採集時間間隔為7天,採集得到的觀測數據表示為yd(s,t)。利用本發明方法對三維溫度傳感數據進行分析的具體實施方式如下。
1)根據研究對象的溫度場的特徵,建立混合效應模型。
研究對象可以是工程領域中任何與溫度場有關的物質溫度場,例如倉儲中的糧食溫度場,某一地區的環境溫度場,人體體溫場。混合效應模型的框架如下:假設y(s,t)表示三維溫度場在時空點(s,t)的溫度值,s和t分別表示空間和時間的自變量,混合效應模型的框架為:
y(s,t)=μ(s,t)+w(s,t)+∈(s,t)(式1)
其中,μ(s,t)表示在時空點(s,t)處的均值函數項,用來刻畫溫度場的全局溫度變化情況;w(s,t)表示在時空點(s,t)處的局部變化項,用來刻畫溫度場的局部溫度變化情況;∈(s,t)表示在時空點(s,t)處的隨機噪聲項,用來刻畫由隨機或不可控因素引起的溫度變化情況,通常假設其為白噪聲。下面,將分別對均值函數項μ(s,t)和局部變化項w(s,t)建立模型。
2)均值函數項μ(s,t)的建模
充分考慮研究對象的物理屬性,建立均值模型並求解。
b1.均值模型的建立
溫度場的變化通常是由環境因素引起的。本發明中,充分考慮環境因素的影響,在笛卡爾坐標系下,對均值函數項μ(s,t)建立三維非穩態傅立葉傳熱模型:
式2中,μ(x,y,z,t)表示在笛卡爾坐標系下的均值函數項,其中空間坐標s={x,y,z},x、y和z分別表示在x、y和z方向的坐標;ρ表示物質的密度,c表示物質的比熱容,λx,λy和λz分別表示在三維笛卡爾坐標系下物質沿x,y和z方向的熱導率。
b2.均值模型的求解
採用有限差分法對式2求解,實現方法為:
其中(i,j,k,m)表示坐標(x,y,z,t)對應的網格位置,δx,δy,δz和δt分別表示空間、時間方向的網格間隔。為保證這種數值解法的精確度,參數的選取應保證給定初始溫度值及邊界溫度值,採用有限差分法即可實現對均值函數的求解。
均值模型是基於研究對象的物理意義建立的,不涉及溫度場的觀測數據,用於描述理想狀態下溫度場的全局變化。
3)局部變化項w(s,t)的建模
充分考慮溫度場的時空相關性,結合高斯隨機場與克裡金模型建立局部溫度變化模型。
c1.高斯隨機場確定模型框架
假設在時刻tm(m=1,2,…,m),局部溫度變化具有空間平穩性,採用高斯隨機場模型描述si點的溫度與其相鄰位置溫度的關係,即在給定si點相鄰位置溫度值的條件下,si點的溫度與服從於正態分布:
其中,sj~si表示si和sj在高斯隨機場中處於相鄰位置,ωij(tm)表示在tm時刻的空間權重參數,σ2(si,tm)表示條件方差。
c2.克裡金模型確定權重參數
採用克裡金模型確定權重參數ωij(tm),實現方法為:
其中,ωij(tm)表示si點相對其所有相鄰位置sj的權重參數,c(si,sj)表示si與sj的協方差矩陣,c(sj,sj)表示sj之間的協方差矩陣。協方差矩陣是由協方差函數計算得到,協方差函數的表達式如下:
其中sp和sq分別表示p和q點處的空間坐標,在笛卡爾坐標系下,sp={xp,yp,zp}和sq={xq,yq,zq};為在tm時刻下協方差函數的參數,將η={{η(t1),η(t2),…,{η(tm)}記為協方差參數。
c3.協方差參數求解
在初始時刻t1,使用t1時刻的觀測數據yd(s,t1),採用極大似然估計方法求解協方差參數。為了刻畫溫度場的時間相關性,採用貝葉斯估計方法對t2到tm時刻的協方差參數進行更新。假設已知t1到tm-1時刻的協方差參數及觀測數據yd(s,t1:m-1)(m=2,…,m),通過式7得到tm時刻協方差參數的預測分布:
p(η(tm)|yd(s,t1:m-1))=∫p(η(tm)|η(tm-1))p(η(tm-1)|yd(s,t1:m-1))dη(tm)(式7)
其中,p(η(tm)|yd(s,t1:m-1))表示在已知t1到tm-1時刻觀測數據yd(s,t1:m-1)的條件下,tm時刻的協方差參數η(tm)的概率密度;p(η(tm)|η(tm-1))表示在已知tm-1時刻的協方差參數η(tm-1)的條件下,tm時刻的協方差參數η(tm)的概率密度;p(η(tm-1)|yd(s,t1:m-1))表示在已知t1到tm-1時刻觀測數據yd(s,t1:m-1)的條件下,tm-1時刻的協方差參數η(tm-1)的概率密度。
再通過式8,利用tm時刻的觀測數據yd(s,tm)實現協方差參數的更新,即求協方差參數的後驗概率密度分布p(η(tm)|yd(s,t1:m)):
其中:
p(yd(s,tm)|yd(s,t1:m-1))=∫p(yd(s,tm)|η(tm))p(η(tm)|yd(s,t1:m-1))dη(tm)(式9)
p(yd(s,tm)|η(tm))表示在tm時刻的協方差參數η(tm)的條件下,yd(s,tm)的概率密度。由於參數的分布是非正態的,因此採用粒子濾波方法實現貝葉斯估計的迭代計算。
4)估計得到時空溫度場中任何位置的溫度
協方差參數估計之後,給定觀測數據yd(s,t),便可實現對溫度場中任何位置的溫度的估計。
其中,在tm時刻點的溫度估計值。
下面通過實例對本發明做進一步說明。
實施例:
以中國華中地區某一國家儲備糧庫為例,建立倉儲過程中三維糧食溫度場的估計模型。糧溫數據是通過溫度傳感器採集得到,記為觀測數據yd(s,t),s∈s,t∈t,其中s表示觀測數據的空間自變量s的取值範圍,t表示觀測數據的時間自變量t的取值範圍。在本例中,s的定義如下:糧食溫度場的規格為26m*46m*6m,傳感器的布局為在長、寬方向相鄰傳感器的間隔為5m,在高度方向相鄰傳感器的間隔為1.8m。t的定義如下:糧溫數據的採樣時間為2012年1月31日至2013年3月4日,每隔7天採集一組傳感器數據,共73組數據。
下面建立三維動態糧食溫度場估計模型:
(1)建立混合效應模型的框架
假設y(s,t)表示三維溫度場在時空點(s,t)的溫度值,s和t分別表示空間和時間的自變量,混合效應模型的框架為
y(s,t)=μ(s,t)+w(s,t)+∈(s,t)(式1)
其中,μ(s,t)表示在時空點(s,t)處的均值函數項,用來刻畫溫度場的全局溫度變化情況;w(s,t)表示在時空點(s,t)處的局部變化項,用來刻畫溫度場的局部溫度變化情況;∈(s,t)表示在時空點(s,t)處的隨機噪聲項,用來刻畫由隨機或不可控因素引起的溫度變化情況,通常假設其為白噪聲。下面,將分別對均值函數項μ(s,t)和局部變化項w(s,t)建立模型。
(2)均值函數μ(s,t)模型的建立與求解
糧食溫度場的變化與外界環境溫度及糧食自身傳熱有關。在此,外界環境溫度對糧食溫度的影響,在笛卡爾坐標系下,對均值函數項μ(s,t)建立三維非穩態傅立葉傳熱模型:
式2中,μ(x,y,z,t)表示在笛卡爾坐標系下的均值函數項,其中空間坐標s={x,y,z},x、y和z分別表示在x、y和z方向的坐標;ρ表示物質的密度,c表示物質的比熱容,λx,λy和λz分別表示在三維笛卡爾坐標系下物質沿x,y和z方向的熱導率。本例中的糧食品種為小麥,其密度ρ為750kg/m2,比熱容c為0.15w/(m·k),熱導率λx,λy,λz為2000j/(kg·k)。
採用有限差分法對上述傅立葉傳熱模型求解,實現方法為:
其中,(i,j,k,m)表示時空坐標(x,y,z,t)對應的網格位置,δx,δy,δz和δt分別表示時空方向的網格間隔,即δx=0.5m,δy=0.5m,δz=0.3m,δt=24h。給定初始糧食溫度及邊界條件的溫度值(糧倉邊界溫度的變化是由外界環境溫度引起的),採用有限差分法即可實現對均值函數的求解。
(3)局部變化項w(s,t)的建立與協方差參數求解
高斯隨機場確定模型框架為:假設在時刻tm(m=1,2,…,m),局部溫度變化具有空間平穩性,採用高斯隨機場模型描述si點的溫度與其相鄰位置溫度的關係,即在給定si點相鄰位置溫度值的條件下,si點的溫度與服從於正態分布:
其中,sj~si表示si和sj在糧倉中的距離最近的傳感器的位置,ωij(tm)表示在tm時刻的空間權重參數,σ2(si,tm)表示條件方差。
採用克裡金模型確定權重參數ωij(tm),實現方法為:
其中,ωij(tm)表示si點相對其在糧倉中的距離最近的傳感器的位置sj的權重參數,c(si,sj)表示si與sj的協方差矩陣,c(sj,sj)表示sj之間的協方差矩陣。協方差矩陣是由協方差函數計算得到,協方差函數的表達式如下:
其中sp和sq分別表示p和q點處的空間坐標,在笛卡爾坐標系下,sp={xp,yp,zp}和sq={xq,yq,zq};為在tm時刻下協方差函數的參數,將η={{η(t1),η(t2),…,{η(tm)}記為協方差參數。
在初始時刻t1,使用t1時刻的觀測數據yd(s,t1),採用極大似然估計方法求解協方差參數。為了刻畫溫度場的時間相關性,採用貝葉斯估計方法對t2到tm時刻的協方差參數進行更新。假設已知t1到tm-1時刻的協方差參數及觀測數據yd(s,t1:m-1)(m=2,…,m),通過式7得到tm時刻協方差參數的預測分布:
p(η(tm)|yd(s,t1:m-1))=∫p(η(tm)|η(tm-1))p(η(tm-1)|yd(s,t1:m-1))dη(tm)(式7)
其中,p(η(tm)|yd(s,t1:m-1))表示在已知t1到tm-1時刻觀測數據yd(s,t1:m-1)的條件下,tm時刻的協方差參數η(tm)的概率密度;p(η(tm)|η(tm-1))表示在已知tm-1時刻的協方差參數η(tm-1)的條件下,tm時刻的協方差參數η(tm)的概率密度;p(η(tm-1)|yd(s,t1:m-1))表示在已知t1到tm-1時刻觀測數據yd(s,t1:m-1)的條件下,tm-1時刻的協方差參數η(tm-1)的概率密度。
再通過式8,利用tm時刻的觀測數據yd(s,tm)實現協方差參數的更新,即求協方差參數的後驗概率密度分布p(η(tm)|yd(s,t1:m)):
其中:
p(yd(s,tm)|yd(s,t1:m-1))=∫p(yd(s,tm)|η(tm))p(η(tm)|yd(s,t1:m-1))dη(tm)(式9)
p(yd(s,tm)|η(tm))表示在tm時刻的協方差參數η(tm)的條件下,yd(s,tm)的概率密度。由於參數的分布是非正態的,因此採用粒子濾波方法實現貝葉斯估計的迭代計算。協方差參數估計的結果如圖2所示。
(4)時空溫度場估計
協方差參數估計之後,給定觀測數據yd(s,t),便可實現對溫度場中任何位置的溫度的估計。
其中,在tm時刻點的溫度估計值。圖3為糧食溫度變化曲線,列舉了一部分糧食溫度場的估計結果,其中,圖例中數字是採樣點的空間坐標。圖3表明,任一空間位置的溫度是隨著時間發生動態變化的,且相鄰空間位置的溫度變化規律相近。
需要注意的是,公布實施例的目的在於幫助進一步理解本發明,但是本領域的技術人員可以理解:在不脫離本發明及所附權利要求的精神和範圍內,各種替換和修改都是可能的。因此,本發明不應局限於實施例所公開的內容,本發明要求保護的範圍以權利要求書界定的範圍為準。
