一種基於蝙蝠算法的光譜變量選擇方法與流程

2023-10-23 00:11:07 2

本發明屬於分析化學領域的無損分析技術，具體涉及一種基於蝙蝠算法的光譜變量選擇方法。

背景技術：

光譜分析技術如紫外光譜、紅外光譜、拉曼光譜、近紅外光譜等具有分析速度快、靈敏度高等優勢，已廣泛地應用於石油、農業、醫藥、化工、環境和生物等許多領域。但是複雜樣品的光譜存在噪聲、背景以及信號重疊等問題，因此須藉助於化學計量學方法才能進行定性定量分析。常規的建模方法是對所有的光譜數據都進行建模，但是光譜數據一般存在成百上千的變量，且並不是所有變量都能提供有用信息，故而會影響預測模型的質量，導致其預測能力下降，因此，需要在建模之前進行變量選擇。

傳統的變量選擇方法主要包括基於智能優化算法的方法以及基於統計學的方法。前者主要有模擬退火算法、遺傳算法、蟻群算法、粒子群算法、人工魚群算法等，儘管模擬退火算法和遺傳算法具有相當強的搜索能力，但它們也存在需要大量參數、較長搜索時間以及容易陷入局部最優等缺陷。後者主要有無信息變量消除法(Uninformative Variable Elimination，UVE)、蒙特卡羅-無信息變量消除法(Monte Carlo-Uninformative Variable Elimination，MC-UVE)、隨機檢驗-偏最小二乘法(Randomization Test-Partial Least Square，RT-PLS)等。無信息變量消除法採用留一法交叉驗證來獲取變量穩定性值，該過程除需多次反覆運算外，還需引入與原始光譜所包含變量數目相等的隨機噪聲變量，所以當數據集數目較大時，該方法存在計算效率低，耗時長等缺點。因此，還需要進一步發展高效準確的變量選擇方法。

蝙蝠算法(BA)是劍橋大學Xin-she Yang教授於2010年提出的元啟發式優化算法，其具有理論方法簡單、設置參數少、編碼實現易的特點，算法通過模擬蝙蝠的覓食以及回聲定位行為，改變頻率、響度和脈衝發射率，進行最佳解的搜索，直到目標達到或停止條件得到滿足。蝙蝠算法在工業上常用於連續優化問題，然光譜數據都是離散的數據點，因而傳統連續優化的蝙蝠算法無法直接應用於光譜變量選擇。本發明對蝙蝠算法進行離散化，並應用於光譜數據的變量選擇，用偏最小二乘回歸(PLS)建立模型，從而提出了一種基於蝙蝠算法的光譜變量選擇方法。既簡化了模型，又提高了模型的預測精度。

技術實現要素：

本發明的目的是針對上述存在的問題，對蝙蝠算法進行離散化，並應用於光譜數據的變量選擇，用PLS對所選擇的變量建立模型，從而達到簡化模型及改善模型預測能力的目的。

為實現本發明所提供的技術方案包括以下步驟：

1)採集一定數目樣品的光譜，用常規方法測定樣品中被測成分的含量；採用一定的分組方式，將數據集劃分為訓練集和預測集。

2)將訓練集的整個光譜範圍劃分為若干個子區間，蝙蝠個體用一串二進位碼表示，對應子區間的選擇與否用「1」與「0」表示。

3)利用公式(1)和(2)將蝙蝠個體位置進行離散化。

其中，t表示迭代次數，k表示維數，vi表示速度，xi表示蝙蝠的位置。

4)對蝙蝠算法的初始化參數進行優化，依次優化迭代次數、響度以及脈衝頻率、蝙蝠數目。

首先對迭代次數進行優化。固定蝙蝠數目、響度和頻度，迭代次數從1變化到500，間隔為10，計算不同迭代次數下的預測均方根誤差。預測均方根誤差最小值對應的迭代次數為最佳迭代次數。

其次對響度和頻度進行優化。迭代次數採用最佳值，蝙蝠數目固定為某個值，響度和頻度分別從0.1變化到0.9，間隔為0.1，採用兩個循環，計算不同響度和頻度下的預測均方根誤差。預測均方根誤差最小值對應的響度和頻度為最佳響度和頻度。

最後對蝙蝠數目進行優化。迭代次數、響度、頻度採用最佳值，蝙蝠數目從10變化到40，間隔為5，計算不同蝙蝠數目下的預測均方根誤差。預測均方根誤差最小值對應的蝙蝠數目為最佳蝙蝠數目。

5)利用優化好的參數，採用蝙蝠算法進行變量區間選擇，輸出最佳的光譜子區間組合。

6)利用所選擇的變量區間，建立PLS模型，將預測集中相應的被選擇的變量區間代入PLS模型中，進行預測。

本發明提出的Bat-PLS方法既簡化了模型，又有效地改善了模型的預測能力，進而提高了模型的預測精度。

附圖說明

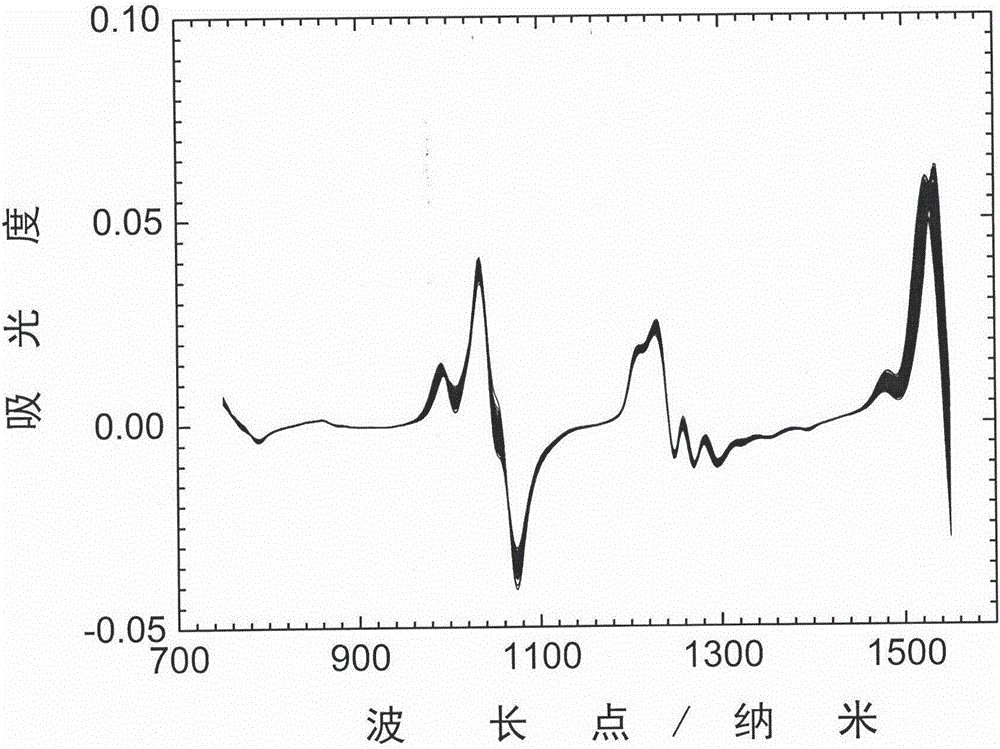
圖1是柴油近紅外數據的光譜圖

圖2是柴油近紅外數據的預測均方根誤差隨迭代次數變化圖

圖3是柴油近紅外數據的蝙蝠數目優化圖

圖4是柴油近紅外數據蝙蝠算法變量選擇方法保留的波長點分布圖

圖5是小麥近紅外數據的光譜圖

圖6是小麥近紅外數據的預測均方根誤差隨迭代次數變化圖

圖7是小麥近紅外數據的蝙蝠數目優化圖

圖8是小麥近紅外數據蝙蝠算法變量選擇方法保留的波長點分布圖

圖9是血液近紅外數據的光譜圖

圖10是血液近紅外數據的預測均方根誤差隨迭代次數變化圖

圖11是血液近紅外數據的蝙蝠數目優化圖

圖12是血液近紅外數據蝙蝠算法變量選擇方法保留的波長點分布圖

圖13是三元調和油近紅外數據的光譜圖

圖14是三元調和油近紅外數據的預測均方根誤差隨迭代次數變化圖

圖15是三元調和油近紅外數據的蝙蝠數目優化圖

圖16是三元調和油近紅外數據蝙蝠算法變量選擇方法保留的波長點分布圖

具體實施方式

為更好地理解本發明，下面結合實施例對本發明做進一步地詳細說明，但是本發明要求保護的範圍並不局限於實施例所表示的範圍。

實施例1：

本實施例應用於近紅外光譜分析，對柴油密度進行測定。具體步驟如下：

1)採集263個柴油密度的近紅外光譜數據，波長範圍為750-1550nm，包括401個波長點，採用網站(http://www.eigenvector.com/Data/SWRI)上對數據集的劃分，將142個樣品用作訓練集，剩餘121個樣品用作預測集。圖1顯示了該數據的近紅外光譜。

2)將訓練集中的401個波長點每10個波長點劃分為1個子區間，共分為40個子區間，最後一個點忽略，蝙蝠個體用40個二進位碼表示，對應子區間的選擇與否用「1」與「0」表示。

3)利用公式(1)和(2)將蝙蝠個體位置進行離散化。

其中，t表示迭代次數，k表示維數，vi表示速度，xi表示蝙蝠的位置。

4)對蝙蝠算法的初始化參數進行優化，依次優化迭代次數、響度以及脈衝頻率、蝙蝠數目。

首先對迭代次數進行優化。固定蝙蝠數為30，響度、頻度均固定為0.5，迭代次數從1變化到500，間隔為10，計算不同迭代次數下的預測均方根誤差。圖2顯示了預測均方根誤差隨著迭代次數的變化，從圖中可以看出，起初隨著迭代次數的增加，預測均方根誤差總體是減小的，當迭代次數大於20之後，隨著迭代次數的增加，預測均方根誤差值趨於平穩，因此，取25為最佳迭代次數。

其次對響度和頻度進行優化。迭代次數採用最佳值25，蝙蝠數目固定為30，響度和頻度從0.1變化到0.9，間隔為0.1，採用兩個循環，計算不同響度和頻度下的預測均方根誤差。預測均方根誤差最小值對應的響度和頻度分別為0.3，0.5。因此最佳響度、頻度分別為0.3，0.5。

最後對蝙蝠數目進行優化。迭代次數採用最佳值25，響度和頻度分別採用最佳值0.3，0.5，蝙蝠數目從10變化到40，間隔為5，計算不同迭代次數下的預測均方根誤差。圖3是柴油近紅外數據的蝙蝠數目優化圖，從圖中可以看出，預測均方根誤差最小值對應的蝙蝠數目為20。因此最佳蝙蝠數目為20。

5)利用優化好的參數：最佳迭代次數為25，最佳響度和頻度分別為0.3和0.5，最佳蝙蝠數目為20。採用蝙蝠算法進行變量區間選擇，輸出最佳的光譜子區間組合。

6)利用所選擇的變量區間(如圖4所示)，建立PLS模型，將預測集中相應的被選擇的變量區間代入PLS模型中，進行預測。

表1顯示了柴油近紅外數據採用不同建模方法的預測結果。從表中可以看出，僅由PLS單一建模的預測均方根誤差值最高，UVE-PLS、MC-UVE-PLS以及RT-PLS算法優化結果相差不大，Bat-PLS預測均方根誤差值最小，相關係數最大。因此，蝙蝠算法變量選擇要優於其他變量選擇方法。

表1 柴油近紅外數據採用不同建模方法的預測結果

實施例2：

本實施例應用於近紅外光譜分析，對小麥組分含量進行測定。具體步驟如下：

1)採集231個小麥樣品的近紅外光譜數據，波長範圍400-2498nm，採樣間隔為2nm，共1050個波長點，根據網上(http//www.graincanada.gc.ca/Quality/Wheat/classes-e.htmo)對數據集的劃分，775個樣品用作訓練集，剩餘107個樣品用作預測集。圖5顯示了該數據的近紅外光譜圖。

2)將訓練集中的1050個波長點按每10個波長點劃分為1個子區間，共分為105個子區間，蝙蝠個體用105個二進位碼表示，對應子區間的選擇與否用「1」與「0」表示。

3)利用公式(1)和(2)將蝙蝠個體位置進行離散化。

其中，t表示迭代次數，k表示維數，vi表示速度，xi表示蝙蝠的位置。

4)對蝙蝠算法的初始化參數進行優化，依次優化迭代次數、響度以及脈衝頻率、蝙蝠數目。

首先對迭代次數進行優化。固定蝙蝠數為30，響度、頻度均固定為0.5，迭代次數從1變化到500，間隔為10，計算不同迭代次數下的預測均方根誤差。圖6顯示了預測均方根誤差隨著迭代次數的變化，從圖中可以看出，隨著迭代次數的增加，預測均方根誤差值是不斷減小的，但是由於迭代次數的限制，當迭代次數為500的時候仍然沒有達到最小值，又由於實驗設備的限制，取500為最佳迭代次數。

其次對響度和頻度進行優化。迭代次數採用最佳值500，蝙蝠數目固定為30，響度和頻度從0.1變化到0.9，間隔為0.1，採用兩個循環，計算不同響度和頻度下的預測均方根誤差。預測均方根誤差最小值對應的響度和頻度分別為0.3，0.4。因此最佳響度、頻度分別為0.3，0.4。

最後對蝙蝠數目進行優化。迭代次數採用最佳值500，響度和頻度分別採用最佳值0.3，0.4，蝙蝠數目從10變化到40，間隔為5，計算不同迭代次數下的預測均方根誤差。圖7是近紅外數據的蝙蝠數目優化圖，從圖中可以看出，預測均方根誤差最小值對應的蝙蝠數目為15。因此最佳蝙蝠數目為15。

5)利用優化好的參數：最佳迭代次數為500，最佳響度和頻度分別為0.3和0.4，最佳蝙蝠數目為15。採用蝙蝠算法進行變量區間選擇，輸出最佳的光譜子區間組合。

6)利用所選擇的變量區間(如圖8所示)，建立PLS模型，將預測集中相應的被選擇的變量區間代入PLS模型中，進行預測。

表2顯示了小麥近紅外數據的採用不同建模方法的預測結果。從表中可以看出，僅由PLS單一建模的效果最差，UVE-PLS、MC-UVE-PLS以及RT-PLS算法相較於PLS的優化結果好了一倍，這三種方法中，RT-PLS建模的效果相對來說差點，但Bat-PLS預測均方根誤差值最小，相關係數最大。因此，蝙蝠算法變量選擇要優於其他變量選擇方法。

表2 小麥近紅外數據的採用不同建模方法的預測結果

實施例3：

本實施例應用於近紅外光譜分析，對血液中血紅蛋白含量進行測定。具體步驟如下：

1)採集231個血液中血紅蛋白含量的近紅外光譜數據，波長範圍1100-2498nm，採樣間隔為2nm，包括701個波長點，光譜採用NIR systems spectrometer model 6500光譜儀測定，根據網站(http://www.idrc-chambersburg.org/shootout2010.html)上對數據集的劃分，將143個樣品用作訓練集，剩餘47個樣品用作預測集。圖9顯示了該數據的近紅外光譜圖。

2)將訓練集中的701個波長點按每10個波長點劃分為1個子區間，共分為70個子區間，最後一個點忽略，蝙蝠個體用70個二進位碼表示，對應子區間的選擇與否用「1」與「0」表示。

3)利用公式(1)和(2)將蝙蝠個體位置進行離散化。

其中，t表示迭代次數，k表示維數，vi表示速度，xi表示蝙蝠的位置。

4)對蝙蝠算法的初始化參數進行優化，依次優化迭代次數、響度以及脈衝頻率、蝙蝠數目。

首先對迭代次數進行優化。固定蝙蝠數為30，響度、頻度均固定為0.5，迭代次數從1變化到500，間隔為10，計算不同迭代次數下的預測均方根誤差。圖10顯示了預測均方根誤差隨著迭代次數的變化，從圖中可以看出，隨著迭代次數的增加，預測均方根誤差是階段性減小的，當迭代次數為170左右時，預測均方根誤差值趨於平穩，因此，取170為最佳迭代次數。

其次對響度和頻度進行優化。迭代次數採用最佳值170，固定蝙蝠數目為30，響度和頻度從0.1變化到0.9，間隔為0.1，採用兩個循環，計算不同響度和頻度下的預測均方根誤差。預測均方根誤差最小值對應的響度和頻度分別為0.4，0.1。因此最佳響度、頻度分別為0.4，0.1。

最後對蝙蝠數目進行優化。迭代次數採用最佳值170，響度和頻度分別採用最佳值0.4，0.1，蝙蝠數目從10變化到40，間隔為5，計算不同迭代次數下的預測均方根誤差。圖11是血液近紅外數據的蝙蝠數目優化圖，從圖中可以看出，預測均方根誤差最小值對應的蝙蝠數目為25。因此最佳蝙蝠數目為25。

5)利用優化好的參數：最佳迭代次數為170，最佳響度和頻度分別為0.4和0.1，最佳蝙蝠數目為25。採用蝙蝠算法進行變量區間選擇，輸出最佳的光譜子區間組合。

6)利用所選擇的變量區間(如圖12所示)，建立PLS模型，將預測集中相應的被選擇的變量區間代入PLS模型中，進行預測。

表3顯示了血液近紅外數據採用不同建模方法的預測結果。從表中可以看出，UVE+PLS方法所得的預測均方根誤差值最大，PLS、MC-UVE+PLS以及RT+PLS算法的預測均方根誤差值稍小一點，Bat-PLS預測均方根誤差值最小，相關係數最大。因此，蝙蝠算法變量選擇要優於其他變量選擇方法。

表3 血液近紅外數據採用不同建模方法的預測結果

實施例4：

本實施例應用於近紅外光譜分析，對三元調和油組分含量進行測定。具體的步驟如下：

1)配置含有大豆油、香油與稻米油的三元調和油樣品50個，其中稻米油、大豆油的濃度範圍為0.05～2.5，間隔為0.05。使用近紅外分光光度計(TJ270-60，天津市拓普儀器有限公司)進行NIR數據測量，波長範圍為800～2500nm，採樣間隔為1nm，共1701個波長點。採用KS方法對數據集進行劃分，將33個樣品用作訓練集，剩餘17個樣品用作預測集。圖13顯示了三元調和油近紅外數據的光譜圖。

2)將訓練集中的1701個波長點按每10個波長點劃分為1個子區間，共分為170個子區間，最後一個點忽略，蝙蝠個體用170個二進位碼表示，對應子區間的選擇與否用「1」與「0」表示。

3)利用公式(1)和(2)將蝙蝠個體位置進行離散化。

其中，t表示迭代次數，k表示維數，v1表示速度，x1表示蝙蝠的位置。

4)對蝙蝠算法的初始化參數進行優化，依次優化迭代次數、響度以及脈衝頻率、蝙蝠數目。

首先對迭代次數進行優化。固定蝙蝠數為30，響度、頻度均固定為0.5，迭代次數從1變化到500，間隔為10，計算不同迭代次數下的預測均方根誤差。圖14顯示了預測均方根誤差隨著迭代次數的變化，從圖中可以看出，隨著迭代次數的增加，預測均方根誤差是不斷減小的，迭代次數將近500時達到最小值，由於實驗設備的限制，因此取500為最優迭代次數。

其次對響度和頻度進行優化。迭代次數採用最佳值500，固定蝙蝠數目為30，響度和頻度從0.1變化到0.9，間隔為0.1，採用兩個循環，計算不同響度和頻度下的預測均方根誤差。預測均方根誤差最小值對應的響度和頻度分別為0.2，0.3。因此最佳響度、頻度分別為0.2，0.3。

最後對蝙蝠數目進行優化。迭代次數採用最佳值500，響度和頻度分別採用最佳值0.2，0.3，蝙蝠數目從10變化到40，間隔為5，計算不同迭代次數下的預測均方根誤差。圖15是三元調和油近紅外數據的蝙蝠數目優化圖，從圖中可以看出，預測均方根誤差最小值對應的蝙蝠數目為30。因此最佳蝙蝠數目為30。

5)利用優化好的參數：最佳迭代次數為500，最佳響度和頻度分別為0.2和0.3，最佳蝙蝠數目為30。採用蝙蝠算法進行變量區間選擇，輸出最佳的光譜子區間組合。

6)利用所選擇的變量區間(如圖16所示)，建立PLS模型，將預測集被選擇的相應變量區間代入PLS模型中，進行預測。

表4顯示了三元調和油近紅外數據採用不同建模方法的預測結果。從表4可以看出，除了Bat-PLS算法所得的預測均方根誤差值明顯小一些，PLS、UVE-PLS、MC-UVE-PLS以及RT-PLS算法所得預測均方根誤差值相差並不太大。因此，蝙蝠算法變量選擇要優於其他變量選擇方法。

表4 三元調和油近紅外數據採用不同建模方法的預測結果