一種實驗模態頻率的丟失辨識及預估方法與流程
2023-10-25 17:03:32 2
本發明涉及一種實驗模態頻率的丟失辨識及預估方法,屬於機械振動技術領域。
背景技術:
通過實驗測量獲得對象的實驗模態頻率的過程中,如果激勵點或拾振點位於某一階模態振型的節點處,亦或是實驗測量平臺系統的噪音對某一階模態頻率具有明顯的幹擾效應,都會引起實驗模態頻率階數丟失的情況發生。
目前,實驗模態頻率階數丟失的解決方案主要有兩種,一種是在對象上採用多點激勵並多點拾取的措施,該方法能夠避免實驗模態頻率階數的丟失,但該方法適用於大中型結構,且需要較大的激勵能量的情況,同時該方法中的各激勵器需反覆調試,致使調試效率低,設備成本高,另一種是將計算模態振型與實驗模態振型進行振型相關性分析,該方法能夠辨識實驗模態頻率丟失的階數,但該方法中的計算量大,計算時間長,致使該方法對實驗模態頻率丟失階數的辨識效率低。
技術實現要素:
本發明正是為了克服上述現有技術的不足而提供的一種實驗模態頻率的丟失辨識及預估方法
本發明的目的是提供一種實驗模態頻率的丟失辨識及預估方法,依據計算模態頻率與實驗模態頻率具有強的正相關性,將實驗模態頻率與相應的計算模態頻率進行相關性分析,進而辨識實驗模態頻率丟失的階數,同時預估相應丟失的實驗模態頻率。該方法克服了多點激勵多點拾取中設備成本高,調試效率低的問題,也克服了計算模態振型與實驗模態振型振型相關性分析中的計算量大,計算時間長,辨識效率低的問題。
本發明是通過如下技術方案來實現的:
一種實驗模態頻率的丟失辨識及預估方法,包括如下步驟:
步驟1在有限元軟體中,導入加載對象的有限元模型;
步驟2在有限元軟體中,設置有限元模型的楊氏模量Ey;
步驟3在有限元軟體中,計算對象的各階模態頻率w1y,w2y……wny;
步驟4通過實驗平臺,測出對象的各階模態頻率w1c,w2c……wnc;
步驟5辨識丟失的實驗模態頻率階數;
步驟6預估丟失的實驗模態頻率。
其中辨識丟失的實驗模態頻率階數的具體步驟包括:
5.1計算k,其中k=w1c/w1y;
5.2令w1=w1c,wj為對象的各階模態頻率,j為對象各階模態頻率的下標號,wic為測出對象的各階模態頻率,i為測出對象各階模態頻率的下標號,wpy為計算對象的各階模態頻率,p為計算對象各階模態頻率的下標號,其中j,i,p均為整數,2≤j,2≤i≤n,2≤p≤z,令j=2,i=2,p=2;
5.3計算m,Δm,b,Δb,其中,
5.4判斷Δm,Δb的大小關係
若Δm≤Δb,則未丟失該階實驗模態頻率,即wj=wic,判斷i是否等於n,若i≠n,則i加1,j加1,p加1,否則輸出對象的各階模態頻率wj,其中n為通過實驗平臺測出對象的模態頻率最大階數,同時捨棄剩餘未使用的計算對象的各階模態頻率;
若Δm>Δb,則為丟失該階實驗模態頻率,即wj=0,判斷i是否等於n,若i≠n,則j加1,p加1,否則輸出對象的各階模態頻率wj,其中n為通過實驗平臺測出對象的模態頻率最大階數,同時捨棄剩餘未使用的計算對象的各階模態頻率;
5.5重複步驟5.3-5.4。
其中預估丟失的實驗模態頻率的具體步驟包括:
6.1依據輸出的wj=0,讀取丟失的相應實驗模態頻率wt,wt+1,wt+2……wt+r以及相鄰的實驗模態頻率wt-1,wt+r+1,其中,t,t+1,t+2……t+r為丟失的實驗模態頻率的下標,t-1,t+r+1為相鄰的實驗模態頻率的下標;
6.2對丟失的實驗模態頻率進行賦值,即wt=uw(t)y,wt+1=uw(t+1)y,wt+2=uw(t+2)y……wt+r=uw(t+r)y,其中u為待求係數,等式右端的t,t+1,t+2……t+r為相應的計算對象各階模態頻率的下標;
6.3構造關於待求係數u的函數f(u),即並求解f(u)最小值時的u;
6.4將所求的係數u代入到步驟302中的等式中,即可預估丟失的實驗模態頻率wt,wt+1,wt+2……wt+r。
本發明具有以下有益效果:
1、能夠減少實驗設備的調試量,提升實驗設備的調試效率;
2、對實驗設備要求低,能夠降低實驗測量成本;
3、能夠減少計算量和計算時間,提高實驗模態頻率丟失階數的辨識效率;
4、能夠預估相應丟失的實驗模態頻率。
附圖說明
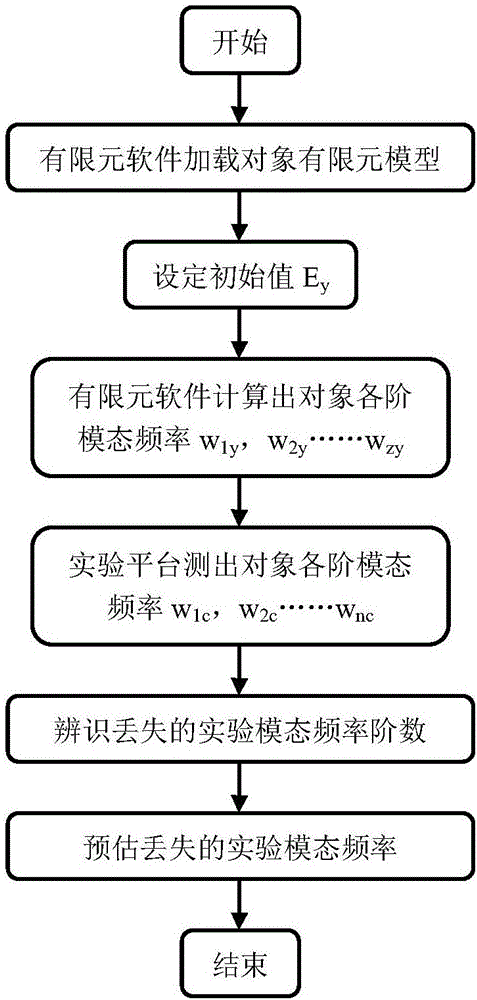
圖1為實驗模態頻率的丟失辨識及預估方法示意圖;
圖2為辨識丟失的實驗模態頻率階數流程圖;
圖3為預估丟失的實驗模態頻率流程圖。
具體實施方式
下面結合附圖和實施例,對本發明作進一步說明,但本發明的內容並不限於所述範圍。
實施例1:如圖1所示,一種實驗模態頻率的丟失辨識及預估方法,包括如下具體步驟:
步驟1在有限元軟體中,導入加載對象的有限元模型;
步驟2在有限元軟體中,設置有限元模型的楊氏模量Ey;
步驟3在有限元軟體中,計算對象的各階模態頻率w1y,w2y…,wpy,…wzy,其中z為通過有限元軟體計算出對象的模態頻率最大階數;
步驟4通過實驗平臺,測出對象的各階模態頻率w1c,w2c…,wic,…wnc,其中n為通過實驗平臺測出對象的模態頻率最大階數,且n≤z;
步驟5辨識丟失的實驗模態頻率階數
如圖2所示,5.1計算k,其中k=w1c/w1y;
5.2令w1=w1c,wj為對象的各階模態頻率,j為對象各階模態頻率的下標號,wic為測出對象的各階模態頻率,i為測出對象各階模態頻率的下標號,wpy為計算對象的各階模態頻率,p為計算對象各階模態頻率的下標號,其中j,i,p均為整數,2≤j,2≤i≤n,2≤p≤z,令j=2,i=2,p=2;
5.3計算m,Δm,b,Δb,其中,
5.4判斷Δm,Δb的大小關係
若Δm≤Δb,則未丟失該階實驗模態頻率,即wj=wic,判斷i是否等於n,若i≠n,則i加1,j加1,p加1,否則輸出對象的各階模態頻率wj,其中n為通過實驗平臺測出對象的模態頻率最大階數,同時捨棄剩餘未使用的計算對象的各階模態頻率;
若Δm>Δb,則為丟失該階實驗模態頻率,即wj=0,判斷i是否等於n,若i≠n,則j加1,p加1,否則輸出對象的各階模態頻率wj,其中n為通過實驗平臺測出對象的模態頻率最大階數,同時捨棄剩餘未使用的計算對象的各階模態頻率;
5.5重複步驟5.3-5.4。
步驟6預估丟失的實驗模態頻率
如圖3所示,6.1依據輸出的wj=0,讀取丟失的相應實驗模態頻率wt,wt+1,wt+2……wt+r以及相鄰的實驗模態頻率wt-1,wt+r+1,其中,t,t+1,t+2……t+r為丟失的實驗模態頻率的下標,t-1,t+r+1為相鄰的實驗模態頻率的下標;
6.2對丟失的實驗模態頻率進行賦值,即wt=uw(t)y,wt+1=uw(t+1)y,wt+2=uw(t+2)y……wt+r=uw(t+r)y,其中u為待求係數,等式右端的t,t+1,t+2……t+r為相應的計算對象各階模態頻率的下標;
6.3構造關於待求係數u的函數f(u),即並求解f(u)最小值時的u;
6.4將所求的係數u代入到步驟302中的等式中,即可預估丟失的實驗模態頻率wt,wt+1,wt+2……wt+r。
實施例2:步驟1在有限元軟體中,導入加載對象的有限元模型。
步驟2在有限元軟體中,設置有限元模型的楊氏模量Ey=1010Pa。
步驟3在有限元軟體中,計算對象的各階模態頻率w1y=10.2Hz,w2y=15.4Hz,w3y=22.6Hz,w4y=32.1Hz,w5y=53.6Hz,w6y=66.7Hz,w7y=72.6Hz。
步驟4通過實驗平臺,測出對象的各階模態頻率w1c=101.3Hz,w2c=153.6Hz,w3c=319.7Hz,w4c=535.5Hz,w5c=666.6Hz。
步驟5辨識丟失的實驗模態頻率階數
5.1令w1=w1c,j=2,i=2,p=2,其中wj為對象的各階模態頻率,j為對象各階模態頻率的下標號,i為測出對象各階模態頻率的下標號,p為計算對象各階模態頻率的下標號;
5.2按照實施例1中的公式計算k,k=w1c/w1y=101.3/10.2=9.93;
5.3計算m,Δm,b,Δb,m=w2c/w2y=153.6/15.4=9.97,Δm=∣9.97-9.93∣/9.93=0.004,b=153.6/22.6=6.8,Δb=∣6.8-9.93∣/9.93=0.315;
5.4判斷Δm,Δb的大小關係
Δm<Δb,則未丟失該階實驗模態頻率,即w2=w2c,其中i=2還沒有取到n即5,所以繼續i加1,j加1,p加1,取j=3,i=3,p=3;
計算新的m,Δm,b,Δb,m=319.7/22.6=14.14,Δm=(14.14-9.93)/9.93=0.42,b=319.7/32.1=9.96,Δb=(9.96-9.93)/9.93=0.003;
新的Δm>Δb,則為丟失該階實驗模態頻率,即w3=0,進一步的,j=4,p=4,繼續計算直到停止。
步驟6預估丟失的實驗模態頻率
6.1依據輸出的w3=0,讀取丟失的相應實驗模態頻率w3,以及相鄰的實驗模態頻率w2=153.6Hz,w4=319.7Hz;
6.2對丟失的實驗模態頻率進行賦值,即w3=uw(3)y=22.6uHz,其中u為待求係數;
6.3構造關於待求係數u的函數f(u),f(u)=(22.6u-22.6k)2,求解f(u)最小值時的u=9.93;
6.4將所求的係數u代入到6.2中的等式中,即可預估丟失的實驗模態頻率w3=226.1Hz。
