一種臨時仰拱或橫撐的受力與變形分析方法與流程
2023-10-27 03:11:15 4
本發明涉及隧道工程領域,具體涉及一種臨時仰拱或橫撐的受力與變形分析方法。
二、
背景技術:
:
設置臨時仰拱或橫撐是軟弱地層隧道常用的一種圍巖大變形控制措施。設置臨時仰拱或橫撐,及時封閉支護結構,不僅可以迅速抑制圍巖的收斂變形,而且可以分擔初支鋼架拱腳的地基荷載從而減小隧道的拱部沉降和地表沉降。目前關於臨時仰拱或橫撐的應用報導已有很多,在作用效果上也進行了一些研究,但現有研究結論只是普遍肯定了臨時仰拱在抑制圍巖收斂變形方面的作用效果,而關於臨時仰拱或橫撐在分擔鋼架拱腳地基荷載以及減小隧道沉降等施工中同樣值得關注的方面,現有的研究均未曾涉及。此外,我國現行的相關隧道設計規範均未給出臨時仰拱或橫撐的力學計算模型和相應的受力分析方法,導致臨時仰拱或橫撐在設計時只能憑經驗選取設計參數。隨著大跨度軟弱地層隧道的不斷湧現,臨時仰拱或橫撐必將大量使用。考慮到隧道臨時仰拱或橫撐與永久仰拱施工工藝和所受支承條件的不同,在缺乏施工經驗的情況下,尋求一種適用於臨時仰拱或橫撐的受力與變形分析方法、為設計提供理論依據成為當務之急。
三、
技術實現要素:
本發明的提供一種臨時仰拱或橫撐的受力與變形分析方法。
為實現上述目的,本發明採用的技術方案為:一種臨時仰拱或橫撐的受力與變形分析方法,其特徵在於:所述的方法步驟為:
步驟1):建立臨時仰拱或橫撐的彈性地基圓弧曲梁模型;
步驟2):根據步驟1)建立的臨時仰拱或橫撐的彈性地基圓弧曲梁模型,,建立臨時仰拱或橫撐的撓曲微分方程,經求解得到臨時仰拱或橫撐撓度、彎矩、剪力、軸力和截面轉角的一般表達式;
步驟3):根據步驟2)得到的臨時仰拱或橫撐撓度、彎矩、剪力、軸力和截面轉角的一般表達式,利用進一步求得臨時仰拱或橫撐在兩端作用相同剪力、彎矩以及軸力時任意截面的內力和變形表達式;
步驟4):根據步驟3)所得臨時仰拱或橫撐在兩端承受相同剪力、彎矩以及軸力時任意截面的內力和變形表達式,進一步得到臨時仰拱或橫撐與鋼架整體求解中所需的鋼架拱腳處的各單位變位和載變位;
步驟5):根據步驟4)所得鋼架拱腳處的各單位變位和載變位,採用力法求解得到鋼架拱頂以及拱腳處的多餘未知力;
步驟6):根據步驟5)得到的鋼架拱頂以及拱腳處的多餘未知力,確定作用於臨時仰拱或橫撐兩端的剪力、彎矩和軸力值;
步驟7):利用步驟6)得到的臨時仰拱或橫撐兩端的剪力、彎矩和軸力值以及步驟3)得到的臨時仰拱或橫撐在兩端分別承受相同剪力、彎矩以及軸力時任意截面的內力和變形表達式,得到在拱部鋼架傳遞的荷載作用下臨時仰拱或橫撐任意截面的撓度、轉角、彎矩、剪力和地基反力值,最終完成臨時仰拱或橫撐的受力與變形分析。
所述步驟1)建立的臨時仰拱或橫撐彈性地基曲梁模型應該滿足以下條件:
A:臨時仰拱或橫撐為彈性地基上的圓弧曲梁,所受徑向地基反力服從溫克爾假定;
B:臨時仰拱或橫撐為彈性體,服從胡克定律;
C:臨時仰拱或橫撐厚度相比圓弧半徑很小,屬於薄梁。
與現有技術相比,本發明具有如下優點和效果:
本發明結合臨時仰拱或橫撐的具體施工工藝,通過考慮拱部鋼架與臨時仰拱仰拱或橫撐以及拱腳下伏地基的共同承載和協調變形,提供一種適用於臨時仰拱或橫撐的受力與變形分析方法,為臨時仰拱或橫撐設計提供理論依據,避免了臨時仰拱或橫撐在設計時僅憑經驗選取設計參數而存在的盲目性。
四、附圖說明:
圖1為臨時仰拱或橫撐力學計算模型及其受力分析方法流程圖;
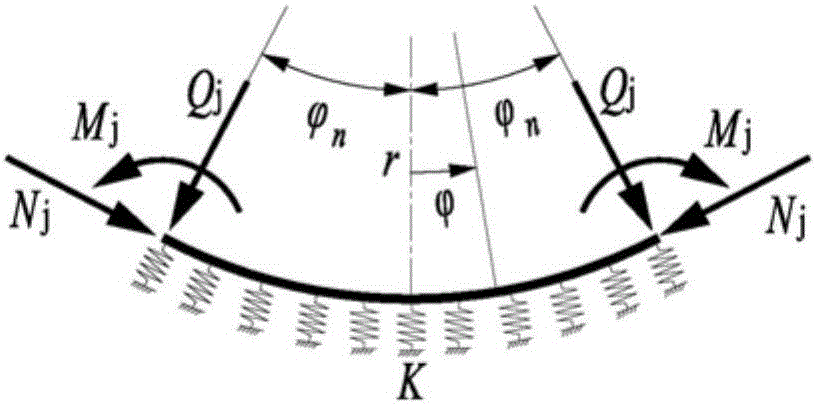
圖2為臨時仰拱或橫撐力學計算模型示意圖;
圖3為臨時仰拱或橫撐微段的受力平衡示意圖;
圖4為臨時仰拱或橫撐兩端作用相同彎矩示意圖;
圖5為臨時仰拱或橫撐兩端作用相同剪力示意圖;
圖6為臨時仰拱或橫撐兩端作用相同軸力示意圖;
圖7為鋼架與臨時仰拱或橫撐的力法基本體系示意圖;
五、具體實施方式
下面結合具體的實施方式來對本發明的技術方案做進一步的詳細說明:
一種臨時仰拱或橫撐的受力與變形分析方法步驟為:
步驟1):建立臨時仰拱或橫撐的彈性地基圓弧曲梁模型;
步驟2):根據步驟1)建立的臨時仰拱或橫撐的彈性地基圓弧曲梁模型,,建立臨時仰拱或橫撐的撓曲微分方程,經求解得到臨時仰拱或橫撐撓度、彎矩、剪力、軸力和截面轉角的一般表達式;
步驟3):根據步驟2)得到的臨時仰拱或橫撐撓度、彎矩、剪力、軸力和截面轉角的一般表達式,利用進一步求得臨時仰拱或橫撐在兩端作用相同剪力、彎矩以及軸力時任意截面的內力和變形表達式;
步驟4):根據步驟3)所得臨時仰拱或橫撐在兩端承受相同剪力、彎矩以及軸力時任意截面的內力和變形表達式,進一步得到臨時仰拱或橫撐與鋼架整體求解中所需的鋼架拱腳處的各單位變位和載變位;
步驟5):根據步驟4)所得鋼架拱腳處的各單位變位和載變位,採用力法求解得到鋼架拱頂以及拱腳處的多餘未知力;
步驟6):根據步驟5)得到的鋼架拱頂以及拱腳處的多餘未知力,確定作用於臨時仰拱或橫撐兩端的剪力、彎矩和軸力值;
步驟7):利用步驟6)得到的臨時仰拱或橫撐兩端的剪力、彎矩和軸力值以及步驟3)得到的臨時仰拱或橫撐在兩端分別承受相同剪力、彎矩以及軸力時任意截面的內力和變形表達式,得到在拱部鋼架傳遞的荷載作用下臨時仰拱或橫撐任意截面的撓度、轉角、彎矩、剪力和地基反力值,最終完成臨時仰拱或橫撐的受力與變形分析。
所述步驟1)建立的臨時仰拱或橫撐彈性地基曲梁模型應該滿足以下條件:
A:臨時仰拱或橫撐為彈性地基上的圓弧曲梁,所受徑向地基反力服從溫克爾假定;
B:臨時仰拱或橫撐為彈性體,服從胡克定律;
C:臨時仰拱或橫撐厚度相比圓弧半徑很小,屬於薄梁。
實施例:
如圖1所示,首先建立臨時仰拱(橫撐)的彈性地基曲梁模型,端部受到拱部鋼架傳遞的彎矩Mj、剪力Qj和軸力Nj,同時受到下伏地基的反力,如圖2所示,並滿足以下條件:
(1)臨時仰拱(橫撐)為彈性地基上的圓弧曲梁,所受徑向地基反力服從溫克爾假定;
(2)臨時仰拱(橫撐)為彈性體,服從胡克定律;
(3)臨時仰拱(橫撐)厚度相比圓弧半徑很小,屬於薄梁。
在圓弧坐標系下,從臨時仰拱(橫撐)上截取曲率半徑為r的任意微段,在和截面上分別附以剪力Q和Q+dQ、彎矩M和M+dM、軸力N和N+dN以及地基反力pdx,各力的正方向如圖3中所示。根據直徑方向和切向方向的受力平衡以及微段的力矩平衡,可得如下三個平衡方程:
dM=Qdx (3)
將p=Kb0y,分別代入式(1)~(3),可得
式(3)對x再求一階導數,有
將式(5)代入式(6),可得
利用式(3),式(7)進一步表示為:
對梁撓曲時彈性曲線的微分方程
分別求一階和三階導數,有
先將式(10)代入式(8),然後再將式(8)代入式(11)可得:
上式為臨時仰拱(橫撐)視為彈性地基圓弧曲梁時的基本微分方程。作變量代換,令則式(12)可進一步表示為:
式(13)的通解可表示為
其中:
將式(14)代入式(1)~(3)和式(9),可得臨時仰拱(橫撐)任一截面的彎矩、剪力及軸力表達式如下:
設坐標原點處截面的轉角為θ0,則臨時仰拱(橫撐)任一截面的轉角可表示為:
由於臨時仰拱(橫撐)的半徑r較大,一般均滿足可視為平曲梁。此時有,α*≈β*≈rλ*=ρ,其中相應地,撓曲時的微分方程(式(9))可近似表示為:
進一步可得
進而由公式(4)可得:
若取對稱軸為豎向坐標軸,則在對稱軸截面處有:和由式(14)和(16)可進一步表示為:α*C2+β*C3=0,β*C2-α*C3=0,可得C2=C3=0。
那麼,臨時仰拱(橫撐)為平曲梁時撓度的一般表達式可簡化表示為:
臨時仰拱為平曲梁時彎矩的一般表達式可簡化表示為:
臨時仰拱為平曲梁時剪力的一般表達式可簡化表示為:
臨時仰拱為平曲梁時軸力的一般表達式可簡化表示為:
N=rKb0C0 (25)
在對稱情況下,在截面處有θ0=0和u0=0,進而將式(23)代入式(18)可得臨時仰拱為平曲梁時截面轉角的一般表達式為:
下面根據臨時仰拱(橫撐)撓度、彎矩、剪力、軸力和截面轉角的一般表達式,進一步求得臨時仰拱(橫撐)在兩端作用相同剪力、彎矩以及軸力時任意截面的內力和變形表達式。
(1)兩端作用相同彎矩
當臨時仰拱(橫撐)兩端作用相同彎矩時,如圖4所示,根據兩端邊界條件:可得:
進而可得:
(2)兩端作用相同剪力
當臨時仰拱(橫撐)兩端作用相同剪力時,如圖5所示,根據兩端邊界條件:可得:
進而可得:
(3)兩端作用相同軸力
當臨時仰拱(橫撐)兩端作用相同軸力時,如圖6所示,根據兩端邊界條件:和可得:C1=0,C4=0。
進而可得:
臨時仰拱(橫撐)作為平曲梁,根據以上分析,當兩端同時作用有相同彎矩Mj、剪力Qj和軸力Nj時,利用疊加原理可求得式(22)~(26)中的未知係數為:
由於鋼架是彈性固定在臨時仰拱(橫撐)兩端的,在鋼架與臨時仰拱(橫撐)的整體求解過程中,須考慮兩者連接處的變形協調性。臨時仰拱作為平曲梁,其軸力對自身變形的影響非常小而可以忽略,鋼架各拱腳的水平位移和豎向位移可近似取為臨時仰拱(橫撐)端部撓度的水平分量和豎向分量。鑑此,根據臨時仰拱(橫撐)在兩端承受相同剪力、彎矩等時任意截面的內力和變形表達式,可得到臨時仰拱(橫撐)與鋼架整體求解中所需的鋼拱腳處的各單位變位和載變位為:
其中對於淺埋無偏壓隧道有
對於深埋隧道有
所述β1L、β1R、u1L和u1R分別為左、右拱腳截面處同時作用單位力矩時所引起的左、右拱腳截面轉角和水平位移;所述v1L為左、右拱腳截面處同時作用單位力矩時左拱腳截面處的豎向位移;所述β2L、β2R、u2L和u2R分別為左、右拱腳截面處同時作用單位水平力時所引起的左、右拱腳截面轉角和水平位移;所述v2L為左、右拱腳截面處同時作用單位水平力時左拱腳截面處的水平位移;所述β3L、β3R、u3L和u3R分別為左、右拱腳截面處同時作用單位豎向力時所引起的左、右拱腳截面轉角和水平位移;所述v3L為左、右拱腳截面處同時作用單位豎向力時左拱腳截面處的豎向位移;所述βpL、βpR、upL和upR分別為圍巖荷載所引起的左、右拱腳截面轉角和水平位移;所述vpL為圍巖荷載作用下左拱腳截面處的豎向位移;所述q0為隧道總的豎向圍巖荷載,單位為N/m,可按相關隧道設計規範中淺埋隧道和深埋隧道的圍巖壓力計算公式分別進行計算;η為作用於鋼架上的圍巖荷載比例;γ為圍巖容重,單位為N/m3;λ為側壓力係數;l為上臺階開挖跨度,單位為m;f為臨時仰拱(橫撐)上方的隧道開挖高度,單位為m;為臨時仰拱(橫撐)端部相對於隧道中線的夾角,單位為°。
根據鋼架拱腳處的各單位變位和載變位(式(40)~(51)),並採用力法可求得鋼架拱頂以及拱腳處的多餘未知力(見圖7)為:
其中
式中
對於淺埋無偏壓隧道有
對於深埋隧道有
所述多餘未知力X1為鋼架拱頂截面的彎矩,單位為N·m;所述多餘未知力X2為鋼架拱頂截面的軸力,單位為N;所述多餘未知力X3為臨時仰拱(橫撐)支護下鋼架拱腳的地基反力,單位為N;所述Af為鋼架拱腳與基底的接觸面積,單位為m2;所述R為隧道拱部半徑,單位為m;EsIs為鋼架的抗彎剛度,單位為N·m2;所述δ11、δ12、δ21和δ22為鋼架拱腳剛性固定時,X1、X2作用下拱頂截面處分別沿X1、X2方向產生的單位位移;所述Δ1p、Δ2p分別為圍巖荷載作用下鋼架拱腳剛性固定時拱頂截面處分別沿X1、X2方向產生的位移。
在求得鋼架拱頂以及拱腳的多餘未知力X1、X2和X3後,即可確定拱部鋼架作用於臨時仰拱(橫撐)兩端的剪力、彎矩和軸力值分別為:
其中對於淺埋隧道有
對於深埋隧道有
利用上述過程求得的臨時仰拱(橫撐)兩端的剪力值和彎矩值(式(63))以及臨時仰拱(橫撐)任意截面的撓度、轉角、彎矩、剪力和地基反力表達式(式(22)~(26)),得到在拱部鋼架傳遞的荷載作用下臨時仰拱(橫撐)任意截面的撓度、轉角、彎矩、剪力和地基反力值,最終完成臨時仰拱(橫撐)的受力與變形分析。
