往復式發動機的曲軸的製作方法
2023-11-06 11:59:17 8
本發明涉及一種搭載在汽車用發動機、船舶用發動機、發電機等通用發動機這樣的往復式發動機上的曲軸。
背景技術:
往復式發動機為了將活塞在缸體(氣缸)內的往復運動轉換為旋轉運動而輸出動力,需要曲軸。曲軸大致區分為利用模鍛製造的曲軸和利用鑄造製造的曲軸。特別是在要求高強度和高剛度的情況下,大多使用那些特性優異的前者的鍛造曲軸。
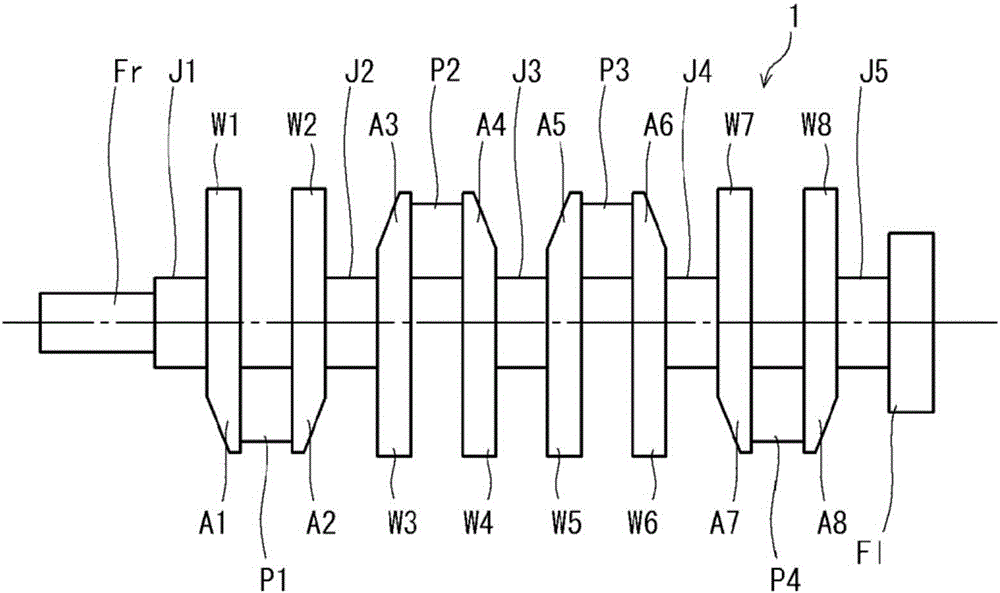
圖1是示意地表示通常的曲軸的一例子的側視圖。圖1所示的曲軸1搭載在四缸發動機上,其包括五個軸頸部J1~J5、四個銷部P1~P4、前端部Fr、凸緣部Fl以及分別將軸頸部J1~J5和銷部P1~P4相連的八塊曲臂部(以下也簡稱作「臂部」)A1~A8。該曲軸1在八塊臂部A1~A8上均一體地具有平衡配重部(以下也簡稱作「配重部」)W1~W8,被稱作四缸-八平衡配重的曲軸。
以下,在分別統稱軸頸部J1~J5、銷部P1~P4、臂部A1~A8以及配重部W1~W8時,將軸頸部的附圖標記記為「J」,將銷部的附圖標記記為「P」,將臂部的附圖標記記為「A」,將配重部的附圖標記記為「W」。將銷部P和與該銷部P相連的一組臂部A(包含配重部W)也統稱作「曲拐(日文:スロー)」。
軸頸部J、前端部Fr以及凸緣部Fl與曲軸1的旋轉中心配置在同軸上。銷部P自曲軸1的旋轉中心偏心活塞衝程的一半距離地配置。軸頸部J利用滑動軸承支承在發動機體上,成為旋轉中心軸。在銷部P上利用滑動軸承連結有連接杆(以下也簡稱作「連杆」)的大端部,在該連杆的小端部利用活塞銷連結有活塞。
在發動機中,在各缸體內燃料爆發。因該爆發而產生的燃燒壓力帶來活塞的往復運動,轉換為曲軸1的旋轉運動。此時,燃燒壓力經由連杆作用於曲軸1的銷部P,並經由與該銷部P相連的臂部A傳遞到軸頸部J。由此,曲軸1一邊反覆彈性變形一邊旋轉。
在用於支承曲軸的軸頸部的軸承上存在潤滑油。與曲軸的彈性變形相對應,軸承內的油膜壓力和油膜厚度與軸承載荷和軸頸部的軸心軌跡互相關聯地變化。而且,與軸承處的軸頸部的表面粗糙度和軸瓦的表面粗糙度相對應,不僅產生油膜壓力,也發生局部的金屬接觸。為了防止由油耗盡引起的軸承燒粘並且防止局部的金屬接觸,確保油膜厚度是重要的。其原因在於,對燃料消耗性能產生影響。
此外,由於由曲軸的旋轉引起的彈性變形和在軸承內的空隙中移動的軸頸部的軸心軌跡引起旋轉中心的偏離,因此,對發動機振動(支座振動)產生影響。而且,該振動在車身中傳播,對車廂內的噪音、乘坐舒適性產生影響。
為了提升這樣的發動機性能,曲軸尋求剛度較高且不易變形。不僅如此,曲軸還尋求輕量化。
對曲軸負載筒內壓力(缸體內的燃燒壓力)的載荷,此外還負載旋轉離心力的載荷。為了施加相對於這些載荷的變形阻力,謀求提升曲軸的扭轉剛度和彎曲剛度。在曲軸的設計過程中決定軸頸部的直徑、銷部的直徑、活塞衝程等這樣的主要規格。在決定了主要規格之後,臂部的形狀設計成為剩下的設計區域。因此,利用臂部的形狀設計同時提升扭轉剛度和彎曲剛度首先成為重要的要素。這裡所說的臂部,像上述那樣,嚴格地講是限定於將軸頸部和銷部相連的區域的長圓形狀(日文:小判形狀)的部分,是不包含平衡配重部的區域的部分。
另一方面,曲軸需要使靜態平衡和動態平衡均衡的質量分配。其目的在於,在運動力學上作為旋轉體能夠進行流暢的旋轉。為了取得這些靜態平衡和動態平衡,相對於根據彎曲剛度和扭轉剛度的要素所決定了的臂部側的質量,在輕量化的基礎上調整配重部側的質量成為重要的要素。
對於靜態平衡而言,針對臂部和配重部的各部分的質量矩(質量×重心半徑),將這些值的全部之和調整為零。此外,對於動態平衡而言,以曲軸的旋轉軸的某一點為基準,將從該基準點到各部分的重心的軸向距離乘以各部分的質量矩(質量×重心半徑×軸向距離),將這些值的全部之和調整為零。
而且,為了在一曲拐內(與一缸相對應的曲軸的區域)取得相對於燃燒壓力載荷的平衡而調整平衡率。平衡率是曲軸的配重部側的質量矩相對於包含銷部(嚴格地講也包含連杆的一部分)的臂部側的質量矩的比例。該平衡率被調整為處於某個恆定範圍內。
謀求提高曲軸的臂部的剛度和輕量化處於折衷的關係,但為了同時達到兩者的要求,一直以來提出了各種與臂部形狀相關的技術。作為以往技術存在下述的內容。
日本專利第4998233號公報(專利文獻1)公開了一種臂部:在臂部的銷部側的表面和軸頸部側的表面的、連結軸頸部的軸心和銷部的軸心的直線(以下也稱作「臂部中心線」)上集中地設有較大地凹入的凹槽。專利文獻1所公開的臂部意在輕量化和提升剛度。軸頸部側表面的凹槽有助於通過質量的減少實現輕量化,而且,該凹槽周圍的厚壁部有助於提升扭轉剛度。但是,鑑於在臂部中心線上集中地存在較大地凹入的凹槽,在實際的狀況中不太能夠期待提升彎曲剛度。
日本特表2004-538429號公報(專利文獻2)、日本特表2004-538430號公報(專利文獻3)、日本特開2012-7726號公報(專利文獻4)以及日本特開2010-230027號公報(專利文獻5)公開了在臂部的軸頸部側的表面的、臂部中心線上設有較大較深地凹入的孔部的臂部。在專利文獻2~5所公開的臂部中,也能夠謀求輕量化和提升扭轉剛度。但是,鑑於在臂部中心線上存在較大較深地凹入的孔部,在實際的狀況中彎曲剛度下降。
現有技術文獻
專利文獻
專利文獻1:日本專利第4998233號公報
專利文獻2:日本特表2004-538429號公報
專利文獻3:日本特表2004-538430號公報
專利文獻4:日本特開2012-7726號公報
專利文獻5:日本特開2010-230027號公報
技術實現要素:
發明要解決的問題
確切地講,採用所述專利文獻1~5所公開的技術,能夠謀求曲軸的輕量化和提升扭轉剛度。但是,在這些以往技術中,曲軸的彎曲剛度的提升存在極限,強烈地盼望其技術革新。
本發明即是鑑於這樣的實際情況而完成的,其目的在於提供一種在謀求曲軸的輕量化和提升扭轉剛度的同時、能夠謀求提升彎曲剛度的往復式發動機的曲軸。
用於解決問題的方案
作為本發明的一個技術方案的往復式發動機的曲軸包括成為旋轉中心軸的軸頸部、相對於該軸頸部偏心的銷部、將所述軸頸部和所述銷部相連的曲臂部、以及與所述曲臂部一體的平衡配重部。所述曲軸搭載在往復式發動機上,經由連接杆在從活塞銷的軸心朝向所述銷部的軸心的方向上對所述銷部負載由燃燒壓力引起的載荷。
在所述曲臂部的所述軸頸部側的表面上,在沿著該表面的輪廓的邊緣部的內側沿著該邊緣部具有凹部。所述凹部相對於將所述銷部的軸心和所述軸頸部的軸心連結的臂部中心線為非對稱。
在由所述燃燒壓力引起的對所述銷部負載的所述載荷成為最大的時刻,所述曲臂部的彎曲剛度成為最大。
上述的曲軸能夠設為所述曲臂部的所述邊緣部的厚度相對於所述臂部中心線為非對稱的結構。
在上述的曲軸中,優選設為下述的結構。
在將所述臂部中心線作為分界地將所述曲臂部劃分為左右的臂部部分時,
在所述曲臂部的與所述臂部中心線垂直的各截面中的、比所述銷部的軸心靠外側的各截面中,被負載所述最大的所述載荷的一側的所述臂部部分的截面慣性矩大於與被負載所述最大的所述載荷的一側相反的那一側的所述臂部部分的截面慣性矩,
在所述曲臂部的與所述臂部中心線垂直的各截面中的、比所述銷部的軸心靠內側的各截面中,與被負載所述最大的所述載荷的一側相反的那一側的所述臂部部分的截面慣性矩大於被負載所述最大的所述載荷的一側的所述臂部部分的截面慣性矩。
在該曲軸的情況下,能夠設為這樣的結構:
在比所述銷部的軸心靠外側的所述各截面中,被負載所述最大的所述載荷的一側的所述臂部部分的最大厚度大於與被負載所述最大的所述載荷的一側相反的那一側的所述臂部部分的最大厚度,
在比所述銷部的軸心靠內側的所述各截面中,與被負載所述最大的所述載荷的一側相反的那一側的所述臂部部分的最大厚度大於被負載所述最大的所述載荷的一側的所述臂部部分的最大厚度。
此外,在上述的曲軸的情況下,也能夠設為這樣的結構:
在比所述銷部的軸心靠外側的所述各截面中,被負載所述最大的所述載荷的一側的所述臂部部分的寬度大於與被負載所述最大的所述載荷的一側相反的那一側的所述臂部部分的寬度,
在比所述銷部的軸心靠內側的所述各截面中,與被負載所述最大的所述載荷的一側相反的那一側的所述臂部部分的寬度大於被負載所述最大的所述載荷的一側的所述臂部部分的寬度。
發明的效果
採用本發明的曲軸,在反映了實際狀態的條件下,在臂部的軸頸部側的表面形成有相對於臂部中心線非對稱的凹部。由此,臂部的邊緣部被厚壁化,該邊緣部的內側利用凹部被薄壁化。進而該凹部的內側的中央部被厚壁化,因此,臂部的彎曲剛度上升,與此同時臂部的輕量化和扭轉剛度上升。
附圖說明
圖1是示意地表示通常的曲軸的一例子的側視圖。
圖2是用於說明臂部的彎曲剛度的評價方法的示意圖。
圖3是用於說明臂部的扭轉剛度的評價方法的示意圖,圖3的(a)表示一曲拐的側視圖,圖3的(b)表示其軸向觀察時的主視圖。
圖4是表示在從材料力學上扭轉剛度的觀點出發將臂部視為單純的圓板的情況下的典型例的圖,圖4的(a)表示矩形截面圓板,圖4的(b)表示凸型截面圓板,圖4的(c)表示凹型截面圓板。
圖5是表示在從材料力學上彎曲剛度的觀點出發使臂部的截面形狀單純化並將臂部視為單純的梁的情況下的典型例的圖,圖5的(a)表示矩形截面梁,圖5的(b)表示凸型截面梁,圖5的(c)表示凹型截面梁。
圖6是與截面形狀相應地歸納與彎曲剛度和扭轉剛度直接相關聯的截面慣性矩和截面極慣性矩的大小關係的圖。
圖7是表示四循環發動機的筒內壓力曲線的圖。
圖8是表示在由燃燒壓力引起的負載成為最大的時刻曲軸的臂部和連杆的幾何學關係的圖。
圖9是表示在燃燒壓力的負載成為最大的時刻曲軸轉角θ和最大載荷負載角α之間的相互關係的圖。
圖10是表示在燃燒壓力的負載成為最大的時刻曲軸的臂部和連杆的幾何學關係的另一例子的圖。
圖11是表示材料力學的梁理論中的梁形狀的一例子的圖,圖11的(a)表示矩形梁,圖11的(b)表示輕量化梁。
圖12是表示利用圖11的(b)所示的輕量化梁的概念做成的左右非對稱的臂部形狀的圖,圖12的(a)表示立體圖,圖12的(b)和圖12的(c)分別表示與臂部中心線垂直的剖視圖。
圖13是表示將臂部形狀設計為在由燃燒壓力引起的載荷成為最大時臂部的彎曲剛度成為最大的圖。
圖14是表示本實施方式的曲軸的臂部形狀的一例子的圖。
圖15是表示本實施方式的曲軸的臂部形狀的另一例子的圖。
圖16是表示本實施方式的曲軸的臂部形狀的另一例子的圖。
圖17是表示本實施方式的曲軸的臂部形狀的另一例子的圖。
圖18是表示以往的曲軸的臂部形狀的一例子的圖。
具體實施方式
以下,詳細地說明本發明的往復式發動機的曲軸的實施方式。
1.在曲軸的設計中應考慮的基本技術
1-1.臂部的彎曲剛度
圖2是用於說明臂部的彎曲剛度的評價方法的示意圖。如圖2所示,就曲軸的各曲拐而言,因缸體內的爆發而產生的燃燒壓力的載荷F經由連杆負載於銷部P。此時,由於各曲拐利用軸承支承兩端的軸頸部J,因此,載荷F從銷部P經由臂部A傳遞到軸頸軸承。由此,臂部A成為3點彎曲的載荷負載狀態,對臂部A作用彎矩M。隨之,在臂部A中,在板厚方向的外側(軸頸部J側)產生壓縮應力,在板厚方向的內側(銷部P側)產生拉伸應力。
在將銷部P和軸頸部J的各直徑作為設計規格並對其進行了決定的情況下,臂部A的彎曲剛度依賴於各曲拐的臂部形狀。配重部W對於彎曲剛度幾乎沒有幫助。此時,如下述的算式(1)所示,銷部P的軸向中央的燃燒壓力負載方向上的位移u與對銷部P負載的燃燒壓力的載荷F成正比,與彎曲剛度成反比。
u∝F/(彎曲剛度)…(1)
1-2.臂部的扭轉剛度
圖3是用於說明臂部的扭轉剛度的評價方法的示意圖。圖3的(a)表示一曲拐的側視圖,圖3的(b)表示該一曲拐的軸向觀察時的主視圖。由於曲軸以軸頸部J為中心地進行旋轉運動,因此,如圖3所示產生扭矩T。因此,需要提高臂部A的扭轉剛度。其目的在於,相對於曲軸的扭轉振動不引起共振而確保流暢的旋轉。
在將銷部P和軸頸部J的各直徑作為設計規格並對其進行了決定的情況下,臂部A的扭轉剛度依賴於各曲拐的臂部形狀。配重部W對於扭轉剛度幾乎沒有幫助。此時,如下述的算式(2)所示,軸頸部J的扭轉角γ與扭矩T成正比,與扭轉剛度成反比。
γ∝T/(扭轉剛度)…(2)
2.本實施方式的曲軸
2-1.用於提升臂部剛度的見解
像上述那樣,配重部對彎曲剛度和扭轉剛度幾乎沒有幫助。因此,在本實施方式中,提出了輕量且彎曲剛度和扭轉剛度同時上升的臂部形狀。
2-1-1.提升扭轉剛度的基本形狀
在此,基於材料力學的理論對用於提升扭轉剛度的典型的形狀進行研究。就所述圖3所示的臂部A而言,為了維持重量並提升扭轉剛度,增大極慣性矩的做法是有效的。
圖4是表示在從材料力學上扭轉剛度的觀點出發將臂部視為單純的圓板的情況下的典型例的圖。圖4的(a)表示矩形截面圓板,圖4的(b)表示凸型截面圓板,圖4的(c)表示凹型截面圓板。在任一個圖中均是上層表示立體圖,下層表示剖視圖。圖4的(a)所示的矩形截面圓板、圖4的(b)所示的凸型截面圓板以及圖4的(c)所示的凹型截面圓板的各重量相同。即,這些圓板的截面形狀為矩形、凸型以及凹型而互不相同,但它們的體積相同。
具體地講,圖4的(a)所示的矩形截面圓板的截面形狀為矩形,厚度是H0,直徑是B0。圖4的(b)所示的凸型截面圓板的截面形狀是中央部與外周部相比突出的凸型,最外周的直徑是B0。該中央部突出部分的厚度是H2,直徑是B2,該外周部的厚度是H1。另一方面,圖4的(c)所示的凹型截面圓板的截面形狀是中央部與外周部相比凹入的凹型,最外周的直徑是B0。該中央部的厚度是H1,凹坑的深度是H3,凹坑的直徑是B3。
在使重量相同的條件下查驗這些圓板的扭轉剛度的大小關係。一般來講,根據材料力學的理論,在扭轉剛度、極慣性矩以及扭轉角之間存在用下述的算式(3)~算式(5)表示的關係。根據這些算式的關係,增大極慣性矩的做法對於提升扭轉剛度是有效的。
扭轉剛度:G×J/L…(3)
極慣性矩:J=(π/32)×d4…(4)
扭轉角:γ=T×L/(G×J)…(5)
在算式(3)~算式(5)中,L是軸向長度,G是橫向彈性模量,d是圓棒的半徑,T是扭矩。
在圖4所示的3種圓板中,重量相同這樣的條件的意思是指體積相同這樣的條件。因此,這3種圓板的各尺寸參數存在下述的算式(6)的關係。
(π/4)×B0×B0×H0=(π/4)×(B0×B0×H1+B2×B2×H2)=(π/4)×{B0×B0×(H1+H3)-B3×B3×H3)}…(6)
而且,考慮到厚度,用下述的算式(7)~算式(9)表示3種圓板各自的極慣性矩。
矩形截面圓板的極慣性矩:
J(A)=(π/32)×H1×B04…(7)
凸型截面圓板的極慣性矩:
J(B)=(π/32)×(H1×B04+H2×B24)…(8)
凹型截面圓板的極慣性矩:
J(C)=(π/32)×{(H1+H3)×B04-H3×B34}…(9)
根據這些算式(7)~算式(9),矩形截面圓板的極慣性矩J(A)、凸型截面圓板的極慣性矩J(B)以及凹型截面圓板的極慣性矩J(C)的大小關係如下述的算式(10)所示。
J(B)<J(A)<J(C)…(10)
該算式(10)是根據材料力學在理論上導出的結論。定性地講,根據在距扭轉的中心的距離較遠的部位配置有較多構件的截面形狀的方式極慣性矩升高這樣的材料力學的考察,能夠理解該結論。
例如作為相同重量的條件、即滿足上述算式(6)的條件的實例,考慮如下地設定各尺寸參數的情況。
B0=100mm、H0=20mm、H1=10mm、H2=H3=20mm、B2=B3=100/√2=70.71mm。
在該實例的情況下,根據上述算式(7),如利用下述的算式(11)所示那樣求出矩形截面圓板的極慣性矩J(A)。
J(A)=1.96×108…(11)
根據上述算式(8),如利用下述的算式(12)所示那樣求出凸型截面圓板的極慣性矩J(B)。
J(B)=1.47×108…(12)
根據上述算式(9),如利用下述的算式(13)所示那樣求出凹型截面圓板的極慣性矩J(C)。
J(C)=2.45×108…(13)
根據這些算式(11)~算式(13),在數值上能夠確認上述算式(10)的關係成立。
因而,可以說,相對於扭轉載荷,按照凸型截面圓板、矩形截面圓板以及凹型截面圓板的順序扭轉剛度升高,凹型截面圓板是最優選的形狀。
2-1-2.提升彎曲剛度的基本形狀
在此,基於材料力學的理論對用於提升彎曲剛度的典型的形狀進行研究。就所述圖2所示的臂部A而言,為了維持重量並提升彎曲剛度,增大相對於彎曲的截面慣性矩的做法是有效率的。
圖5是表示在從材料力學上彎曲剛度的觀點出發使臂部的截面形狀單純化並將臂部視為單純的梁的情況的典型例的圖。圖5的(a)表示矩形截面梁,圖5的(b)表示凸型截面梁,圖5的(c)表示凹型截面梁。在任一個圖中,均是上層表示立體圖,下層表示剖視圖。圖5的(a)所示的矩形截面梁、圖5的(b)所示的凸型截面梁以及圖5的(c)所示的凹型截面梁的各重量相同。即,這些梁的截面形狀為矩形、凸型以及凹型而互不相同,但這些截面的面積相同。
具體地講,圖5的(a)所示的矩形截面梁的截面形狀為矩形,厚度是H0,寬度是B3。圖5的(b)所示的凸型截面梁的截面形狀是中央部與兩側部相比突出的凸型,整個寬度是B3。該中央部的厚度是H2,寬度是B2,該兩側部分別是厚度為H1,寬度為B1/2。另一方面,圖5的(c)所示的凹型截面梁的截面形狀是中央部與兩側部相比凹入的凹型,整個寬度是B3。該中央部的厚度是H1,寬度是B1,該兩側部分別是厚度為H2,寬度為B2/2。
在使重量相同的條件下查驗這些梁的剛度相對於彎曲載荷的大小關係。一般來講,根據材料力學的理論,用下述的算式(14)~算式(16)表示矩形梁的彎曲剛度和截面慣性矩之間的關係。根據算式(14)~算式(16)的關係,增大截面慣性矩的做法會提高彎曲剛度。
彎曲剛度:E×I…(14)
截面慣性矩:I=(1/12)×b×h3…(15)
撓曲位移:u=k(M/(E×I))…(16)
在算式(14)~算式(16)中,b是寬度,h是厚度,E是縱向彈性模量,M是彎矩,k是形狀係數。
在圖5所示的3種梁中,重量相同這樣的條件的意思是指體積彼此相同、即截面的面積彼此相同這樣的條件。因此,與這3種梁的各尺寸參數相關地存在下述的算式(17)的關係。
B3×H0=(H2×B2+B1×H1)=(H2×B2+B1×H1)…(17)
而且,用下述的算式(18)~算式(20)表示3種梁各自的截面慣性矩。
矩形截面梁的截面慣性矩:
I(D)=(1/12)×B3×H03…(18)
凸型截面梁的截面慣性矩:
I(E)=1/3×(B3×E23-B1×H33+B2×E13)…(19)
在算式(19)中,
E2為「(B2×H22+B1×H12)/{2×(B2×H2+B1×H1)}」,
E1為「H2-E2」,
H3為「E2-H1」。
凹型截面梁的截面慣性矩:
I(F)=1/3×(B3×E23-B1×H33+B2×E13)…(20)
在算式(20)中,
E2為「(B2×H22+B1×H12)/{2×(B2×H2+B1×H1)}」,
E1為「H2-E2」,
H3為「E2-H1」。
上述算式(19)和上述算式(20)的形式相同。這是表示在重量相同這樣的條件下凸型截面梁的截面慣性矩I(E)和凹型截面梁的截面慣性矩I(F)相同。
總而言之,矩形截面梁的截面慣性矩I(D)、凸型截面梁的截面慣性矩I(E)以及凹型截面梁的截面慣性矩I(F)的大小關係如下述的算式(21)所示。
I(D)<I(E)=I(F)…(21)
該算式(21)是根據材料力學在理論上導出的結論。定性地講,根據在距彎曲的中立面的距離較遠的部位配置有較多構件的截面形狀的方式截面慣性矩升高這樣的材料力學的考察,能夠理解該結論。
例如作為相同重量的條件、即滿足上述算式(17)的條件的實例,考慮如下地設定各尺寸參數的情況。
B1=B2=50mm、B3=100mm、H0=20mm、H1=10mm、H2=30mm。此時,E1=12.5mm、E2=17.5mm、H3=7.5mm。
在該實例的情況下,根據上述算式(18),如利用下述的算式(22)所示那樣求出矩形截面梁的截面慣性矩I(D)。
I(D)=6.67×104…(22)
根據上述算式(19),如利用下述的算式(23)所示那樣求出凸型截面梁的截面慣性矩I(E)。
I(E)=2.04×105…(23)
根據上述算式(20),如利用下述的算式(24)所示那樣求出凹型截面梁的截面慣性矩I(F)。
I(F)=2.04×105…(24)
根據這些算式(22)~算式(24),在數值上能夠確認上述算式(21)的關係成立。
因而,可以說,相對於彎曲載荷,凸型截面梁和凹型截面梁具有同等的彎曲剛度,與矩形截面梁相比,使臂部的局部厚壁化這樣的凸型截面梁或者凹型截面梁的彎曲剛度較高,是優選的形狀。
2-1-3.提升彎曲剛度和扭轉剛度的基本形狀的歸納
圖6是與截面形狀相應地歸納與彎曲剛度和扭轉剛度直接相關聯的截面慣性矩和極慣性矩的大小關係的圖。在圖6中,用將矩形截面作為基準「1」的比例針對所述圖4和圖5所示的矩形截面、凸型截面以及凹型截面的每個截面形狀表示極慣性矩和截面慣性矩。
如圖6所示,若截面形狀是凸型或者凹型,則彎曲剛度升高,另一方面,若截面形狀是凹型,則扭轉剛度升高。通過將這些截面形狀組合起來,彎曲剛度和扭轉剛度均上升。因此,為了同時提升彎曲剛度和扭轉剛度,將臂部的截面形狀設計為將凸型和凹型組合而成的形狀的做法是有效的。即,使沿著臂部的輪廓的邊緣部厚壁化,使該邊緣部的內側薄壁化。而且,使作為該薄壁化的部分的內側的中央部(在臂部中心線上靠軸頸部的部分)厚壁化。通過使自臂部的扭轉中心較遠的邊緣部厚壁化的同時使其內側薄壁化,能夠實現輕量化並將扭轉剛度確保得較高。臂部的邊緣部的厚壁化有助於確保彎曲剛度。此外,臂部的中央部的厚壁化有助於確保彎曲剛度。
2-2.用於依據實際狀態提升臂部剛度的想法
圖7是表示四循環發動機的筒內壓力曲線的圖。如圖7所示,在將曲軸的銷部達到壓縮工序的上止點的位置(曲軸轉角θ是0°)作為基準時,在壓縮工序上止點之後立即產生爆發。因此,筒內壓力(缸體內的壓力)在曲軸轉角θ為約8°~20°的時刻成為最大的燃燒壓力。對曲軸負載圖7所示的筒內壓力(燃燒壓力)的載荷,此外還負載旋轉離心力的載荷。此時,在曲軸轉角θ為約8°~20°的時刻,最大的燃燒壓力經由連杆被負載在曲軸的銷部。在曲軸的設計過程中,為了獲得相對於由該最大燃燒壓力引起的載荷的變形阻力,提升彎曲剛度以及扭轉剛度、與此同時減輕重量成為目標。
圖8是表示在由燃燒壓力引起的負載成為最大的時刻曲軸的臂部和連杆的幾何學關係的圖。如圖8所示,燃燒壓力對於銷部P的負載方向是從活塞銷的軸心(連杆4的小端部4S的軸心4Sc)朝向銷部P的軸心Pc的方向。因此,由最大燃燒壓力引起的最大載荷Fmax並不是沿著將銷部P的軸心Pc和軸頸部J的軸心Jc連結的臂部中心線Ac的方向負載在臂部A上,而是沿著相對於該臂部中心線Ac傾斜的方向負載在臂部A上。即,反映實際狀態地對曲軸轉角θ為約8°~20°的狀態的臂部A負載最大載荷Fmax。即,在相對於臂部中心線Ac以角度α傾斜的方向上負載最大載荷Fmax。
以下,將由燃燒壓力引起的載荷對於臂部A的負載方向(從活塞銷的軸心朝向銷部的軸心的方向)與臂部中心線Ac的交叉角也稱作載荷負載角β。在載荷負載角β中,曲軸轉角θ為約8°~20°且負載由最大燃燒壓力引起的最大載荷Fmax的時刻的載荷負載角也稱作最大載荷負載角α。
圖9是表示在燃燒壓力的負載成為最大的時刻曲軸轉角θ和最大載荷負載角α之間的相互關係的圖。如所述圖7所示,與彎曲載荷相關,氣缸內的燃燒壓力顯示最大值的是曲軸自壓縮工序上止點稍稍旋轉且曲軸轉角θ為約8°~20°的時刻。
如圖8所示,臂部A在相對於臂部中心線Ac以最大載荷負載角α傾斜的方向上承受由最大燃燒壓力引起的最大載荷Fmax。利用由負載最大燃燒壓力的時刻的曲軸轉角「θ」、活塞衝程Ls的一半(銷部P的軸心Pc和軸頸部J的軸心Jc之間的距離)「Ls/2」、以及連杆4的小端部4S的軸心4Sc(活塞銷的軸心)和銷部P的軸心Pc之間的距離「Lc」這一角兩邊決定的三角形的外角求出該最大載荷負載角α。即,臂部A承受相對於臂部中心線Ac以比曲軸轉角θ(約8°~20°)大一些的最大載荷負載角α(約十度~二十多度)傾斜的彎曲載荷(參照圖9)。
圖10是表示在燃燒壓力的負載成為最大的時刻曲軸的臂部和連杆的幾何學關係的另一例子的圖。圖10所示的發動機中,軸頸部J的軸心Jc的位置(曲柄旋轉軸)偏移地配置在自缸體中心軸線稍稍偏離的位置。或者,雖然軸頸部J的軸心Jc的位置配置在缸體中心軸線上,但是活塞銷的軸心的位置偏移地配置在自缸體中心軸線稍稍偏離的位置。在這種情況下,在幾何學上考慮到與在所述圖8中說明的方式同樣的三角形和偏移量Lo地求出最大載荷負載角α。
2-2-1.本實施方式的曲軸的概要
像上述那樣,最大的彎曲載荷沿相對於臂部中心線以最大載荷負載角α傾斜的方向負載在臂部上。著眼於這一點,以下表示將自輕量且剛度較高的梁的形狀使臂部形狀成為左右非對稱的做法是有效的。
圖11是表示材料力學的梁理論中的梁形狀的一例子的圖。圖11的(a)表示矩形梁,圖11的(b)表示輕量化梁。利用材料力學上的梁理論單純化地考慮臂部。就承受彎曲載荷的梁而言,剛度較高、變形較小、最輕量的二維的梁形狀(板厚t恆定)並不是圖11的(a)所示那樣的、板寬B恆定的矩形梁,而是圖11的(b)所示那樣的、板寬B從載荷點朝向固定端而單調地增大的輕量化梁。
圖12是表示利用圖11的(b)所示的輕量化梁的概念做成的左右非對稱的臂部形狀的圖。圖12的(a)表示立體圖,圖12的(b)和圖12的(c)表示與臂部中心線垂直的剖視圖。圖12所示的臂部形狀的概念還根據上述算式(21)所表示的彎曲剛度升高的結果反映了圖5的(b)的凸型形狀。在此,圖12的(b)表示比銷部的軸心靠外側的截面、即自銷部的軸心靠與軸頸部相反側的截面。圖12的(c)表示比銷部的軸心靠內側的截面、即自銷部的軸心靠軸頸部的截面。所述圖8和圖10所示那樣的、在相對於臂部中心線Ac以最大載荷負載角α傾斜的方向上負載最大的彎曲載荷的臂部A視為圖12的(a)所示那樣多個板厚t的梁堆疊合成的結構。只要將該多個梁的截面形狀設為圖11的(b)所示那樣的、板寬B朝向固定端單調地增加的輕量化梁,就能夠得到最輕量且剛度較高的臂部A。
若如圖12的(a)所示以與臂部中心線Ac垂直的平面切斷該臂部A,則根據幾何學的關係,該截面如圖12的(b)和圖12的(c)所示以臂部中心線Ac為分界地成為左右非對稱的形狀。即,臂部A以臂部中心線Ac為分界地被劃分為左右的臂部部分Ar、Af,右側的臂部部分Ar和左側的臂部部分Af相對於臂部中心線Ac為非對稱。
通過這樣相對於以最大載荷負載角α對臂部A負載的最大彎曲載荷將臂部A做成左右非對稱的形狀,輕量且有效率地剛度升高。臂部A的非對稱形狀考慮有很多。例如,只要以如圖13所示使載荷負載角β作為參數變化且在該載荷負載角β為最大載荷負載角α的時刻(即由燃燒壓力引起的載荷的負載成為最大的時刻)彎曲剛度成為最大的方式將臂部A設計為左右非對稱的形狀,就能夠實現沒有多餘部分的最有效率的輕量化。由此,臂部A最輕量且成為高剛度,能夠最大限度地發揮曲軸的性能。
另外,此時,還優選的是,如圖12的(b)所示,在比銷部的軸心靠外側的截面中,左側的臂部部分Af的截面慣性矩大於右側的臂部部分Ar的截面慣性矩,該左側為被負載最大載荷的一側,該右側為與被負載最大載荷的一側相反的那一側。與此同時,優選的是,如圖12的(c)所示,在比銷部的軸心靠內側的截面中,右側的臂部部分Ar的截面慣性矩大於左側的臂部部分Af的截面慣性矩,該右側為與被負載最大載荷的一側相反的那一側,該左側為被負載最大載荷的一側。
依據以上內容,本實施方式的曲軸在臂部A的軸頸部J側的表面上,在沿著該表面的輪廓的邊緣部的內側沿著該邊緣部形成有凹部。這是遵照上述算式(10)所表示的結果、為了提高扭轉剛度而反映了凹型形狀的曲軸。而且,在反映載荷負載的實際狀態的條件下,該凹部相對於臂部中心線Ac為非對稱。由此,臂部A的形狀相對於臂部中心線Ac成為左右非對稱的形狀。即,臂部A的形狀設為在由燃燒壓力引起的對銷部P負載的載荷成為最大的時刻彎曲剛度成為最大的形狀。由此,臂部的凹部外側的邊緣部被厚壁化,該邊緣部的內側利用凹部被薄壁化。進而,該薄壁化的部分的內側被厚壁化。因此,彎曲剛度上升,與此同時能夠謀求輕量化和提升扭轉剛度。
2-2-2.臂部的形狀例
圖14是表示本實施方式的曲軸的臂部形狀的一例子的圖。圖15是表示其另一例子的圖。圖16和圖17是表示其又一例子的圖。圖17是表示以往的曲軸的臂部形狀的一例子的圖。在圖14~圖18中的任一個圖中,均是各圖的(a)表示一曲拐的立體圖,各圖的(b)表示各圖的(a)中的與臂部中心線垂直的C-C』位置的剖視圖。而且,各圖的(c)表示各圖的(a)中的與臂部中心線垂直且與C-C』位置不同的D-D』位置的剖視圖。在此,各圖的(b)所示的C-C』位置是比銷部的軸心靠外側的位置。此外,各圖的(c)所示的D-D』位置是比銷部的軸心靠內側的位置。
圖14、圖15、圖16及圖17所示的臂部A在軸頸部J側的表面形成有凹部10。具體地講,臂部A具有沿著軸頸部J側的表面輪廓的邊緣部11。凹部10在該邊緣部11的內側沿著該邊緣部11形成。
特別是,分別形成在將臂部中心線Ac作為分界的右側的臂部部分Ar和左側的臂部部分Af上的凹部10的形狀互不相同。具體地講,為了在由燃燒壓力引起的對銷部P負載的載荷成為最大的時刻臂部A的彎曲剛度成為最大,凹部10相對於臂部中心線Ac設為左右非對稱。由此,臂部A相對於臂部中心線Ac為左右非對稱形狀。並且,如各圖的(b)所示,在比銷部P的軸心靠外側的截面中,左側的臂部部分Af的截面慣性矩大於右側的臂部部分Ar的截面慣性矩,該左側為被負載最大載荷的一側,該右側為該左側的相反側。與此同時,如各圖的(c)所示,在比銷部P的軸心靠內側的截面中,右側的臂部部分Ar的截面慣性矩大於左側的臂部部分Af的截面慣性矩,該右側為與被負載最大載荷的一側相反的那一側,該左側為該右側的相反側。
在圖14所示的臂部A中,邊緣部11的厚度相對於臂部中心線Ac為對稱。此外,右側的臂部部分Ar中的邊緣部11的厚度Bar和左側的臂部部分Af中的邊緣部11的厚度Baf相等。取而代之,左側的臂部部分Af在比銷部P的軸心靠外側的截面中,其中央部的最大厚度Bbf大於右側的臂部部分Ar的最大厚度Bbr(參照圖14的(b))。另一方面,在比銷部P的軸心靠內側的截面中,其中央部的最大厚度Bbf小於右側的臂部部分Ar的最大厚度Bbr(參照圖14的(c))。
在圖15所示的臂部A中,邊緣部11的厚度相對於臂部中心線Ac為非對稱。此外,右側的臂部部分Ar中的邊緣部11的厚度Bar與左側的臂部部分Af中的邊緣部11的厚度Baf不同。具體地講,左側的臂部部分Af在比銷部P的軸心靠外側的截面中,其邊緣部11的厚度Baf大於右側的臂部部分Ar的邊緣部11的厚度Bar(參照圖15的(b))。另一方面,在比銷部P的軸心靠內側的截面中,其邊緣部11的厚度Baf小於右側的臂部部分Ar的邊緣部11的厚度Bar(參照圖15的(c))。此外,左側的臂部部分Af的邊緣部11的厚度Baf大於中央部的最大厚度Bbf。該關係在比銷部P的軸心靠外側的截面和比銷部P的軸心靠內側的截面中均成立。在右側的臂部部分Ar中,也同樣是臂部Ar的邊緣部11的厚度Bar大於中央部的最大厚度Bbr。該關係在比銷部P的軸心靠外側的截面和比銷部P的軸心靠內側的截面中均成立。
圖16所示的臂部A是將圖15所示的臂部A變形而成的。不同點如下。就圖16所示的臂部A而言,在比銷部P的軸心靠外側的截面中,左側的臂部部分Af的寬度Wf大於右側的臂部部分Ar的寬度Wr(參照圖16的(b)),在比銷部P的軸心靠內側的截面中,左側的臂部部分Af的寬度Wf小於右側的臂部部分Ar的寬度Wr(參照圖16的(c))。
圖17所示的臂部A是將圖16所示的臂部A變形而成的。不同點如下。在圖17所示的臂部A中,邊緣部11的厚度和中央部的最大厚度相對於臂部中心線Ac為對稱。
另一方面,圖18所示的以往的臂部A沒有形成凹部,是將臂部中心線Ac作為分界地左右對稱形狀。
這樣,在圖14~圖17所示的本實施方式的曲軸中,與圖18所示的以往的曲軸相比較,臂部A是在反映實際狀態的條件下形成的。具體地講,臂部A的邊緣部11在臂部A的整個區域內被厚壁化。該邊緣部11的內側利用凹部10被薄壁化。進而,該薄壁化的部分的內側的中央部被厚壁化。其結果,曲軸能夠謀求輕量化和提升扭轉剛度,與此同時能夠謀求提升彎曲剛度。
此外,本發明並不限定於上述的實施方式,能夠在不脫離本發明主旨的範圍內進行各種變更。例如,本發明的曲軸將搭載在所有的往復式發動機上的曲軸作為對象。即,發動機的缸數除了四缸之外,也可以是一缸、兩缸、三缸、六缸、八缸以及十缸中的任一種,也可以更多。發動機氣缸的排列也並不特別拘於直列配置、V型配置、相對配置等。發動機的燃料也並不拘於汽油、柴油、生物燃料等種類。此外,發動機也包含將內燃機和電動馬達複合而成的混合動力發動機。
產業上的可利用性
本發明能夠有效地應用於搭載在所有的往復式發動機上的曲軸。
附圖標記說明
1、曲軸;J、J1~J5、軸頸部;Jc、軸頸部的軸心;P、P1~P4、銷部;Pc、銷部的軸心;Fr、前端部;Fl、凸緣部;A、A1~A8、曲臂部;Ac、臂部中心線;Ar、右側的臂部部分;Af、左側的臂部部分;W、W1~W8、平衡配重部;4、連接杆;4S、小端部;4Sc、小端部的軸心(活塞銷的軸心);10、凹部;11、邊緣部。
