一種兩軸車輛質心高度的靜態測量方法與流程
2023-10-18 11:04:09 1
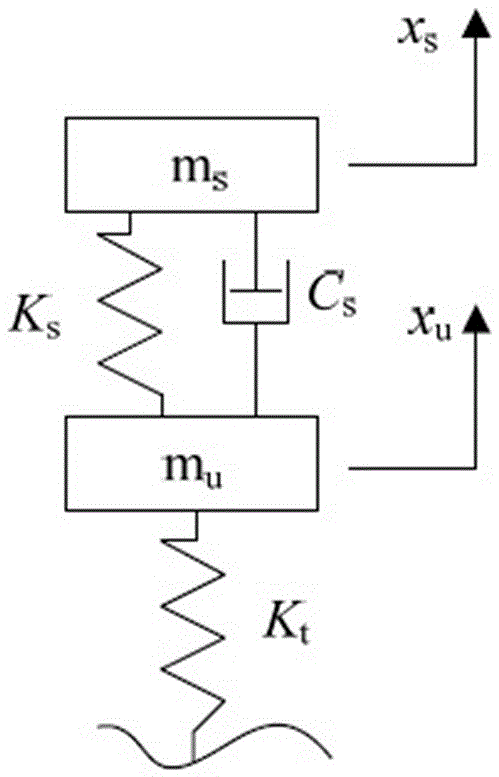
本發明屬於車輛測量技術領域,具體涉及一種兩軸車輛質心高度的靜態測量方法的專利申請。
背景技術:
汽車質心高度是汽車動力控制中的一個重要參數,其對汽車的側傾穩定性、操縱穩定性有著非常重要的作用。特別是罐車、泵車及 SUV 等質心較高的車輛,在極限工況下極易側翻,且側翻事故的危害程度通常極大。
配置主動側傾控制系統的現代車輛往往需要準確測量質心高度,由於質心高度的測量是最為重要但又最為不易測量的參數之一,因此對汽車質心高度的精確測量具有重要的應用意義。
目前,國內外測定汽車質心高度的方法主要有搖擺法、質量反應法、劃線法等靜態測量法和動態測量法等。現有的靜態測量方法,往往需要固定懸架,因而使得測量過程較為費時費力,並且固定不牢時會產生測量誤差,並且這種測定方法無法測量簧載質量和非簧載質量的質心位置;而採用動態法測量時往往需要昂貴的傳感器和採集處理系統,並且易於受信號噪聲的影響,使得測量精度不高。因此研究、開發一種測量精度較好、成本較低、且測定較為快速的汽車質心高度測量方法,具有重要的實用意義。
技術實現要素:
本發明的目的是提供一種車輛質心高度靜態精確測量方法,從而較好解決現有車輛質心靜態測量中需要固定懸架、無法區分測量簧載質量和非簧載質量質心位置、費時費力等弊端。
本申請所採取的技術方案詳述如下。
一種兩軸車輛質心高度的靜態測量方法,該方法包括如下步驟:
(1)首先,確保測試路面水平,然後根據被測車輛輪距和軸距擺放好軸重儀;車輛駛入軸重儀後,熄火發動機,並將車輛掛空擋和駐車檔;
通過鉛錘儀或鋼直尺分別在前輪接地點、輪心及翼子板處用記號筆標註點 A、Of 和 Pf,並確保這三點在一條直線上;
同樣在後輪接地點、輪心及翼子板處標註出點 B、Or和 Pr,測出或根據汽車出廠參數確定軸距 L;
記錄如下測量數據:前輪壓扁半徑 AOf、前輪中心到前標記點 Pf距離 OfPf、後輪壓扁半徑 BOr、後輪中心到後標記點 Pr 的距離 OrPr;
(2)首先,根據前後軸重儀的讀數,分別記錄為 Nf 和 Nr,根據下述公式計算得出整車質量,計算公式為:
m=(Nf+Nr)/g,
式中,g 為重力加速度;
其次,根據力矩平衡方程,確定整車質心距前軸距離:
;
最後,設整車質心為點 O,通過鉛錘儀在車身上畫出一鉛垂線 OC,即該鉛垂線通過整車質心O,質心高度 hx即為待測參數;
(3)通過滾下法進行偏頻實驗,具體為:
將汽車駛上臺階,熄火發動機,停車掛空擋,將汽車從臺階上推下,推下時應儘量保證左右車輪同時落地,在車身處和輪心處布置加速度傳感器;
考慮到輪胎徑向剛度遠大於懸架剛度,可將單軸兩自由度垂直振動模型簡化為單軸單自由度振動模型,這樣便於利用後續步驟識別出前、後軸的簧載質量msf和msr;
(4)根據車身處加速度時域曲線,可以得到系統有阻尼振蕩周期 Td,第 i 個波峰幅值 Ai,第 i+n個波峰幅值 Ai+n;
根據如下公式求得阻尼比ξ:
;
根據如下公式求得固有頻率ωn:
;
懸架彈簧剛度係數 Ks根據如下方法測量獲得:改變前軸或後軸載荷,測得輪心與車身標記點之間距離變化獲得;
然後根據如下公式求得前後軸的簧載質量 msf 和 msr:
;
再求得整車簧載質量:ms=msf+msr;
根據質量平衡原理,求出整車簧載質量ms質心距後軸的距離Lsr :
;
設簧載質心為 Os,待求參數整車簧載質心高度hs;
(5)求出非簧載質量mu:
mu=m-ms;
設非簧載質量 mu質心為 Ou,且該點必在直線 OsO 上;
根據質量平衡原理,計算獲得非簧載質量質心 Ou 距前軸的距離 Luf :
;
計算獲得非簧載質量 mu的質心高度hu:
;
即,下一步通過實驗確定兩個未知量 hx和 hs 的值即可;
(6)通過舉升機構託起前軸重儀一定高度Δ,並通過式如下公式計算出汽車傾斜角度α:
;
考慮到駐車安全性,車輛傾斜角度不宜超過 30%;
讀出前後軸重儀讀數 Nfi和 Nri;
記錄如下測量數據:
前輪壓扁半徑 AOfi、前輪中心到前標記點 Pfi距離 OfiPfi,後輪壓扁半徑 BOri、後輪中心到後標記點 Pri距離 OriPri;
計算獲得汽車前輪壓扁半徑變化量Δrfi=AOfi -AOf;
計算獲得前軸懸架高度變化量Δsfi=OfiPfi-OfPf;
計算獲得後輪壓扁半徑變化量Δrri=AOri -AOr;
計算獲得後軸懸架高度變化量Δsri=OriPri-OrPr;
進而做出因輪胎壓扁半徑變化引起的非簧載質量質心高度變化量Δhui的幾何圖,並得出:
;
做出因懸架變形引起的簧載質量質心高度變化量Δhsi的幾何關係圖,並得出:
;
做出因非簧載質量質心高度變化Δhui 和簧載質量質心高度變化Δhsi引起的整車質心高度變化Δhxi的幾何關係圖,並得出:
;
即,前軸舉升時整車質心高度為 hxi=hx+Δhxi;
(7)對前輪接地點取矩,得出前軸舉升時的力矩平衡方程:
;
解此方程,得質心高度 hxi:
;
並最終得到車輛水平放置時的質心高度:
;
該式裡含有未知量 hs;為此,須再改變一次車輛傾斜角度,並另外得到一個車輛水平放置時的質心高度h′x的表達式,並有:
hx=h′x,
根據該式可求出未知量 hs,然後把 hs代入hx或h′x即可。
考慮到測量誤差,為提高測量精度,可進行多次實驗;同時為了提高測量精度和實驗安全,抬升車輛時傾斜角度不宜過小和過大,可分別選擇 10º、15º、20º、25º,最後取平均值得出‾hx,即為車輛質心高度近似真值。
應用本申請時,首先根據車輛軸荷發生變化時,輪胎壓扁半徑和懸架發生變形,簧載質量和非簧載質量質心高度發生變化,採用劃線法測算出各自變化量;然後根據車輛處於不同傾斜角度與前後軸載荷間關係,根據力矩均衡原理和質量平衡原理,確定各變化量之間的幾何關係,並對車輛的前輪與地面的接觸點取矩,建立力矩平衡方程,得出車輛水平放置狀態下的整車質心高度、簧載和非簧載質量質心高度。
本發明區別於現有靜態車輛質心高度測量方法,本發明不需要固定懸架,只需要多測量幾個尺寸,就可以避免固定懸架帶來的繁重的勞動和安全事故,也可以減小由於固定不牢而產生的測量誤差,同時還可以得出簧載質量和非簧載質量質心位置。測量方法簡單、經濟、精確,廣泛適用於兩軸車輛。
附圖說明
圖 1 汽車水平放置時實驗示意圖;
圖 2 二自由度模型;
圖 3 單自由度模型;
圖 4 車身響應曲線;
圖 5 汽車傾斜放置時實驗示意圖;
圖 6 因輪胎壓扁變形引起的非簧載質量質心高度變化幾何關係;
圖 7 因懸架變形引起的簧載質量質心高度變化量Δhsi 幾何圖;
圖 8 因非簧載質量和簧載質量質心高度變化引起的整車質心高度變化幾何關係圖。
具體實施方式
下面結合實施例對本申請做進一步的解釋說明。
實施例1
本申請所提供的兩軸車輛質心高度的靜態測量方法,該方法包括如下步驟:
(1)首先,確保測試路面水平,然後根據被測車輛輪距和軸距擺放好軸重儀;車輛駛入軸重儀後,熄火發動機,並將車輛掛空擋和駐車檔;
通過鉛錘儀或鋼直尺分別在前輪接地點、輪心及翼子板處用記號筆標註點 A、Of 和 Pf,並確保這三點在一條直線上;
同樣在後輪接地點、輪心及翼子板處標註出點 B、Or和 Pr,測出或根據汽車出廠參數確定軸距 L;
如圖1所示,記錄如下測量數據:前輪壓扁半徑 AOf、前輪中心到前標記點 Pf距離 OfPf、後輪壓扁半徑 BOr、後輪中心到後標記點 Pr 的距離 OrPr。
(2)首先,根據前後軸重儀的讀數,分別記錄為 Nf 和 Nr,根據下述公式計算得出整車質量,計算公式為:
m=(Nf+Nr)/g,
式中,g 為重力加速度;
其次,根據力矩平衡方程,確定整車質心距前軸距離:
;
最後,設整車質心為點 O,通過鉛錘儀在車身上畫出一鉛垂線 OC,即該鉛垂線通過整車質心O,質心高度 hx即為待測參數。
(3)通過滾下法進行偏頻實驗,具體為:
將汽車駛上臺階,熄火發動機,停車掛空擋,將汽車從臺階上推下,推下時應儘量保證左右車輪同時落地,在車身處和輪心處布置加速度傳感器;
考慮到輪胎徑向剛度遠大於懸架剛度,可將單軸兩自由度垂直振動模型(如圖2所示)簡化為單軸單自由度振動模型(如圖3所示)。
(4)根據車身處加速度時域曲線(如圖4所示),可以得到系統有阻尼振蕩周期 Td,第 i 個波峰幅值 Ai,第 i+n個波峰幅值 Ai+n;
根據如下公式求得阻尼比ξ:
;
根據如下公式求得固有頻率ωn:
;
懸架彈簧剛度係數 Ks根據如下方法測量獲得:改變前軸或後軸載荷,測得輪心與車身標記點之間距離變化獲得;
然後根據如下公式求得前後軸的簧載質量 msf 和 msr:
;
再求得整車簧載質量:ms=msf+msr;
根據質量平衡原理,求出整車簧載質量ms質心距後軸的距離Lsr :
;
設簧載質心為 Os,待求參數整車簧載質心高度hs。
(5)求出非簧載質量mu:
mu=m-ms;
設非簧載質量 mu質心為 Ou,且該點必在直線 OsO 上;
根據質量平衡原理,計算獲得非簧載質量質心 Ou 距前軸的距離 Luf :
;
計算獲得非簧載質量 mu的質心高度hu:
;
即,下一步通過實驗確定兩個未知量 hx和 hs 的值即可。
(6)通過舉升機構託起前軸重儀一定高度Δ,並通過式如下公式計算出汽車傾斜角度α(如圖5所示):
;
考慮到駐車安全性,車輛傾斜角度不宜超過 30%;
讀出前後軸重儀讀數 Nfi和 Nri;
記錄如下測量數據:
前輪壓扁半徑 AOfi、前輪中心到前標記點 Pfi距離 OfiPfi,後輪壓扁半徑 BOri、後輪中心到後標記點 Pri距離 OriPri;
計算獲得汽車前輪壓扁半徑變化量Δrfi=AOfi -AOf;
計算獲得前軸懸架高度變化量Δsfi=OfiPfi-OfPf;
計算獲得後輪壓扁半徑變化量Δrri=AOri -AOr;
計算獲得後軸懸架高度變化量Δsri=OriPri-OrPr;
進而做出因輪胎壓扁半徑變化(如圖6所示)引起的非簧載質量質心高度變化量Δhui的幾何圖,並得出:
;
做出因懸架變形(如圖7所示)引起的簧載質量質心高度變化量Δhsi的幾何關係圖,並得出:
;
做出因非簧載質量質心高度變化(如圖8所示)Δhui 和簧載質量質心高度變化Δhsi引起的整車質心高度變化Δhxi的幾何關係圖,並得出:
;
即,前軸舉升時整車質心高度為 hxi=hx+Δhxi;
(7)對前輪接地點(如圖5所示)取矩,得出前軸舉升時的力矩平衡方程:
;
解此方程,得質心高度 hxi:
;
並最終得到車輛水平放置時的質心高度:
;
該式裡含有未知量 hs;為此,須再改變一次車輛傾斜角度,並另外得到一個車輛水平放置時的質心高度h′x的表達式,並有:
hx=h′x,
根據該式可求出未知量 hs,然後把 hs代入hx或h′x即可。
為提高測量精度,可進行多次實驗;同時為了提高測量精度和實驗安全,抬升車輛時傾斜角度不宜過小和過大,可分別選擇 10º、15º、20º、25º,最後取平均值得出‾hx。
