一種監測GIS局部放電的超高頻傳感器布點方法與流程
2024-02-07 11:31:15 1
本發明屬於局部放電在線監測領域,特別涉及一種監測gis局部放電的超高頻傳感器布點方法。
背景技術:
特高頻(ultra-high-frequency,uhf)檢測法是一種利用特高頻傳感器的局放檢測技術。gis內部結構等同於一個同軸波導結構,在局部放電發生時非常有利於電磁波的傳播,這種方法的檢測頻段為300~3000mhz,通過內置或外置的特高頻傳感器接收到的由gis腔體洩露出來的局部放電電磁波信號進行檢測。一般在現場進行局部放電測量時,環境的幹擾頻段通常小於300mhz。檢測特高頻的電磁波可以有效防止電暈等幹擾,具有高靈敏度和高信噪比的有點,並且通過傳感器接收到電磁波信號的時間差就能實現對放電的定位,特高頻法要優於傳統的檢測方法。
特高頻傳感器的響應速度和靈敏性是進行特高頻定位的關鍵,影響傳感器效果的因素主要包括傳感器的類型、空間布局和檢測頻帶等。通過特高頻法進行局部放電的三維空間定位一般需要3個及以上的傳感器,通常把多個傳感器稱為傳感器陣列。特高頻傳感器的空間布局是進行定位計算的關鍵,對定位的精確度至關重要。傳感器布置不合理,定位準確度會下降甚至失效。在每個結點都布置監測裝置是不經濟的。因此,在考慮gis拓撲結構的基礎上,引出了局部放電測量點的優化布置問題。
如何根據電磁波信號與局部放電源的關係特性和電磁波的傳播特性,探索特高頻傳感器在gis內部的位置布點原則是研究的關鍵問題之一。
技術實現要素:
本發明所要解決的技術問題是解決gis現場局放實時監測中在每個節點都布置超高頻傳感器是很不經濟的這一問題,在考慮gis拓撲結構的基礎上,提出了局部放電測量點的優化布置的超高頻傳感器布點方法。
本發明為解決上述技術問題採用以下技術方案
一種監測gis局部放電的超高頻傳感器布點方法,具體包含如下步驟:
步驟1,將gis的各個節點進行編號,將各個節點間的拓撲關係、線路長度繪製成表格;
步驟2,根據各個節點間的拓撲關係畫出此gis的無向圖;
步驟3,計算各線路對所有節點的臨界點,並利用臨界點對整個gis分段,進而獲取0-1規劃模型;
步驟4,計算傳播路徑矩陣,並將其代入0-1規劃模型;
步驟5,採用matlab的bintprog函數求解代入傳播路徑矩陣的0-1規劃模型,解得配置向量,得出需要布置傳感器的節點。
作為本發明一種監測gis局部放電的超高頻傳感器布點方法的進一步優選方案,在步驟3中,所述臨界點為局放源產生的電磁波分別經過線路兩端到達傳感器的距離相等的點。
作為本發明一種監測gis局部放電的超高頻傳感器布點方法的進一步優選方案,在步驟3中,所述臨界點的具體計算如下:
其中,為區域線路l對於第k個節點的傳感器的臨界點,為區段始端i到第k個節點的傳感器最短距離,為區段末端j到第k個節點的傳感器最短距離,ll為區域線路l的總長度。
作為本發明一種監測gis局部放電的超高頻傳感器布點方法的進一步優選方案,在步驟4中,所述傳播路徑矩陣g具體如下:
其中,n為區段內節點數,r為臨界點將整個系統分成的區段數,以表示第l條線路上放電電磁波到達第k個節點,通過線路首端和末端的情況,即:表示經過首端i端,為0表示不經過;表示經過末端j端,為0表示不經過。
作為本發明一種監測gis局部放電的超高頻傳感器布點方法的進一步優選方案,在步驟2中,所述0-1規劃模型具體如下:
s.t.g2r×nxn×1≥i2r×1
b2n×nxn×1=b2n×1
其中,n為區段內節點數,wt=[w1,w2,...,wn]為權重向量,表示每個節點安裝測量裝置的傾向,取(0,1)之間的值,xt=[x1,x2,x3…,xn]為所要求的配置向量,值為1的表示需要配置傳感器,為0的表示不需要配置;r為臨界點將整個系統分成的區段數,g為上面提到的傳播路徑矩陣,b和b分別為係數矩陣和右端向量,若第k個節點能安裝傳感器,則b(k,k)=1,b(k)=1;否則b(k+n,k)=1,b(k)=0。
有益效果
本發明採用以上技術方案與現有技術相比,具有以下技術效果:
1.本發明所提及的布點方法針對於現在gis現場實時監測時需要在每一段間隔的節點處布置超高頻傳感器的問題,提出了一種監測gis局部放電的超高頻傳感器布點方法;
2.本發明適用於複雜拓撲結構的gis,保護範圍無死區,定位準確,且不需要在gis的每一個節點設置超高頻傳感器,節約時間和成本,可以利用大量現有的投運檢測設備,實現簡單,具有較強的經濟性和較好的實用價值。
附圖說明
圖1是本發明線路臨界點示意圖。
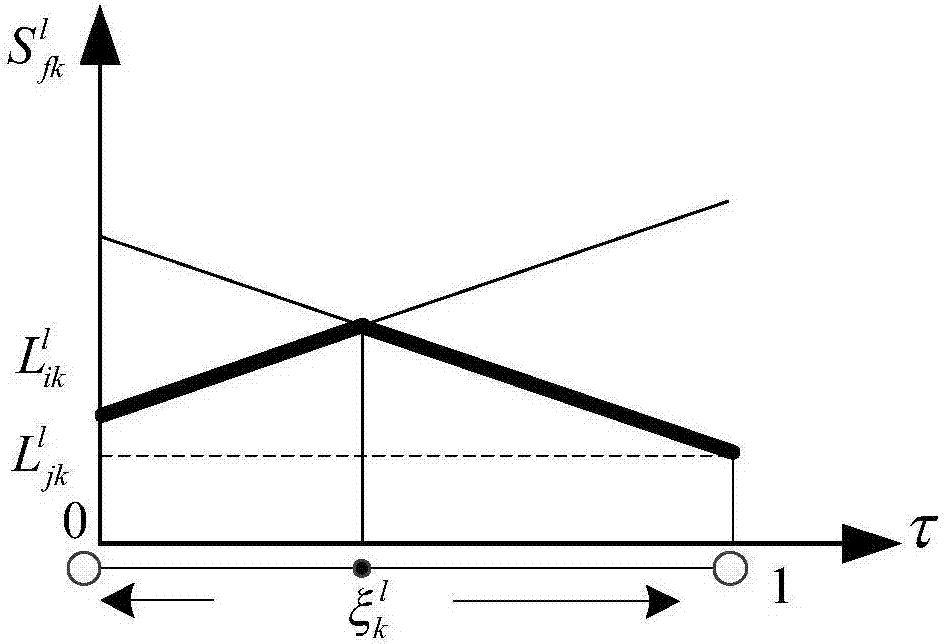
圖2是本發明函數圖像;
圖3是本發明gis系統拓撲結構的無向圖;
圖4本發明具體實施方案流程圖。
具體實施方式
下面結合附圖對本發明的技術方案做進一步的詳細說明:
1.一種監測gis局部放電的超高頻傳感器布點方法,如圖4所示,包含以下步驟:
(1)將gis各個節點編號,節點間的拓撲關係、線路長度繪製成表格,根據節點間的拓撲關係畫出此gis系統的無向圖。
(2)計算各線路對所有節點的臨界點,並利用臨界點對整個gis系統分段,最終求解得到0-1規劃模型。
2.1以xk作為節點是否安裝傳感器的標誌,
其中,1≤k≤n,n為節點總數。
以表示第l區段的放電點f產生的電磁波到達節點k的最短距離即:
其中,1≤l≤m,m為gis區段總數,τ為放電點到始端距離佔整段線路長度的比例,i、j分別表示線路l的始端和末端。又可表示為:
以表示第l條線路上放電電磁波到達第k個節點,通過線路端點的情況即:
根據以上分析,第l條線路完全可測的必要條件是,對於1≤k≤n,至少有一個為1,至少有一個為1。這樣就能保證線路l放電電磁波能從線路兩端分別到達一對傳感器。對於所有線路,都滿足此條件時,則整個系統是完全可測的。因此,可以將系統的最大可觀性問題抽象成0-1規劃模型:
2.2一個gis區段可以解得n個臨界點,即一個節點對應一條區段的一個臨界點,將它們從小到大排序,即有
某些臨界點的值可能相等,即一個臨界點值對應多個節點,取唯一的值並重新排序:
記錄每個臨界點值對應的節點,並放入集合ks中,1≤s≤n,n<n。系統的臨界點圖如圖1所示,0、1代表區段首端和末端。一般情況下即區段l始端到對端的最短距離經過本線路,如果經過相鄰線路,則會出現臨界點最小值和最大值不為0和1的情況。臨界點將每個區段分成n+1個子區間,即若或則區間或長度為0。
2.3對於任意的1<s≤n,區間內放電電磁波到達k1,k2,…ks-1中的節點經過末端j距離更近,到達ks,ks+1,…kn中的節點經過始端i更近,因此總能經過線路兩端到達不同的節點。於是,若k中的節點都安裝傳感器,則區間是完全可觀的。如果區間內的放電電磁波均從i端離開到達k中的節點,為不可測區間。同理如果為不可測區間。因此,線路ij完全可觀的充分必要條件是且
2.4假設這些臨界點將整個系統分成r個小區段,從每個小區段向整個系統看去,區段內的電磁波到達所有節點的路徑便都能知曉。如果將這些區段都看作新的線路,那麼便是可求得的。新系統的不隨放電位置的變化而變化,而是確定的,因此模型(5)便有唯一解。將(0-1)規劃模型表示成矩陣形式:
其中,n為區段內節點數,xt=[x1,x2,...,xn]為待求解的配置向量,wt=[w1,w2,...,wn]為權重向量,表示每個節點安裝測量裝置的傾向,取(0,1)之間的值。第二個不等式表示電磁波到達安裝了傳感器的節點的路徑至少有一對經過區段兩端,r為臨界點將整個系統分成的區段數,所以i=[1,1,...,1]t。第三個等式約束條件約束了某些節點不能安裝節點或者必須安裝節點,若節點k已安裝傳感器,則b(k,k)=1,b(k)=1;若節點k不能安裝傳感器則b(k+n,k)=1;b,b其他元素為0。
為每個區段電磁波到達各個節點的傳播路徑矩陣。
(3)通過優化配置可以達到所有節點都安裝測量裝置的同等的可觀測範圍,即最大可觀性。
所述的臨界點為:如圖2所示,分析始端和末端路徑的圖像。由公式(3)和(4)得
由公式(9),圖像取兩條線段的交點以下部分,即粗實線部分。將兩條線段的交點定義為臨界點令兩條傳播路徑距離相等,即:
解得的
其中,為第l區段的放電點f產生的電磁波到達節點k的最短距離,即為圖像中兩條路徑的分界點,i和j分別為線路的首端和末端,為區域線路l對於第k個節點的傳感器的臨界點,和分別為區段始端i和末端j到第k個節點的傳感器最短距離,ll為區域線路l的總長度。
即為圖像中兩條路徑的分界點,當時,電磁波到達第k個測量點從線路兩端傳播的距離相等,當區間放電時,電磁波經過線路首端,當區間放電時,電磁波經過線路末端,因此可得下式:
進而有:
至此,通過臨界點便確定了電磁波到達每個節點的傳播路徑,而是可以容易求得的。因此,可看作關於τ的分段函數,分段點就是臨界點
所述的優化配置為:通過計算傳播路徑矩陣g,帶入的優化的0-1規劃模型(8),採用matlab的bintprog函數求解此0-1規劃問題,從而得到沒有盲區的gis超高頻傳感器布點模型。
本發明提出一種監測gis局部放電的超高頻傳感器布點方法,下面將參照附圖對本發明方法進行說明。現以一個模型為例進行分析:
將gis各個節點編號,節點間的拓撲關係、線路長度如表1所示。
表1
根據節點間的拓撲關係畫出此gis系統的無向圖,如圖3所示。
由無向圖可看出,系統有兩個相切的環形結構,因此是有可能存在檢測盲區的。在已知線路長度和系統拓撲的情況下,由式(11)不難計算各線路對所有節點的臨界點。各條線路最小與最大臨界點值如表2所示。
表2
可見,所有線路的最小和最大臨界點值均是0和1,因此,這些線路都是完全可測的,不存在盲區。
假設此gis系統沒有安裝傳感器,將權重向量wt內的值全部取1,計算傳播路徑矩陣g,帶入本文的優化的0-1規劃模型(8),採用matlab的bintprog函數求解此0-1規劃問題。最終解得配置向量為x=[1,0,0,0,0,1,0,0,0,0,1,0,0,0,0,0,0,1,0,0,0,0,0,0,1,0,0,0,0],即需要配置傳感器的節點為1,6,11,18,25。將這些點用深色圓圈標註,如圖3所示。可見,終端節點均需要配置傳感器。
