一種高精度星敏感器安裝矩陣在軌實時校準方法與流程
2024-03-06 22:05:15 2
本發明涉及一種高精度星敏感器安裝矩陣在軌實時校準方法。
背景技術:
星敏感器作為目前精度最高的姿態敏感器在航天任務中得到了廣泛應用。傳統星敏感器星光來自單一視場,受視場限制,星間角距較小,導致解算出的光軸方向姿態角精度比另外兩軸姿態角精度低一個數量級,導致三軸姿態精度不一致。當雜散光進視場,或者受空間輻射影響時可能無法穩定可靠的輸出姿態。
為了進一步提高星敏感器的性能,近年來國外出現了多視場星敏感器的概念。如法國sodern公司的hydra星敏感器,美國ball公司的fsc-701星敏感器,日本三菱電機的sis星敏感器以及德國jena-optroni公司的astro-aps星敏感器。與單視場星敏感器相比,對多個視場的觀測信息融合處理,擴大了視場角,提高了光軸方向的精度,使多探頭星敏感器三軸精度一致,可靠性更高。
在多視場觀測信息融合過程中,涉及到各探頭之間的空間關係轉換,探頭之間的安裝矩陣準確與否對最終的融合姿態精度起到決定性作用。在太空飛行器發射之前,通過安裝裝調已經確定了星敏感器各探頭之間的空間關係。受太空飛行器發射過程中的振動,以及在軌熱環境等因素的影響,各探頭的安裝關係並非常值。因此,實時校準探頭之間的安裝關係成為保證多探頭星敏感器精度的關鍵。
星矢量融合需要對不同探頭測量坐標系下的定姿星做空間配準,安裝矩陣的準確性直接影響了融合姿態的精度。由各探頭輸出的四元數直接解算出的實測安裝關係包含了不同頻率的誤差成分,因此不能簡單的做濾波去噪,如果不作處理直接採用該值,測量誤差會導致融合結果無法達到要求。
技術實現要素:
本發明提供一種高精度星敏感器安裝矩陣在軌實時校準方法,可以在軌實時校準補償衛星的結構變形對探頭之間安裝矩陣的影響,具有很強的跟蹤能力和自適應性,用於多探頭星敏感器視場融合中的空間配準,提高融合姿態的精度。
為了達到上述目的,本發明提供一種高精度星敏感器安裝矩陣在軌實時校準方法,包含以下步驟:
步驟s1、解算實測安裝關係四元數;
步驟s2、對安裝關係四元數的矢量部分進行濾波校準;
步驟s3、採用校準後的安裝關係四元數解算安裝矩陣。
在步驟s1中,選定探頭a為基準頭部,由實時輸出的探頭a,探頭b的四元數qa,qb解算探頭a和探頭b之間的實測安裝關係四元數qba:
實測安裝關係四元數qba表示為:
由於四元數的自由度為3,只對其矢部q濾波平滑;
取線性離散系統狀態為則系統方程為:
式中,k為離散時間;系統在時刻k的狀態矢量xk∈r3;yk∈r3為對應狀態的觀測矢量;wk~n(0,qk)為高斯分布的過程激勵噪聲;vk~n(0,rk)為高斯觀測噪聲;d為狀態轉移矩陣;g為觀測矩陣;由於建立的是線性模型,這裡d和g取為三階單位陣。
所述的步驟s2中,對安裝關係四元數的矢量部分進行濾波校準的方法包含以下步驟:
步驟s2.1、輸入線性離散系統狀態量的初始值x0和協方差的初始值p0;
地面安裝裝調時得到安裝關係四元數初值,x0取其矢部,p0任取一量級小於單位陣的非零對角陣;
步驟s2.2、進行狀態一步預測:
xk|k-1=dxk-1(4)
步驟s2.3、計算量測殘差:
vk=yk-gxk|k-1(5)
步驟s2.4、判斷系統是否發散,若收斂判據成立,說明濾波正常,進行步驟s2.5,若收斂判據不成立,說明濾波發散,進行步驟s2.6;
所述的收斂判據為:
式中,γ為儲備係數(γ≥1),γ=1是最嚴格的收斂判據;
步驟s2.5、令衰減因子λk=1,同時由量測殘差在線估計測量噪聲協方差r,進行步驟s2.7
式中,dk=(1-b)/(1-bk+1),b為遺忘因子,一般取0.95~0.99;
步驟s2.6、更新衰減因子,進行步驟s2.7;
步驟s2.7、一步預測協方差陣:
式中,q為過程激勵噪聲協方差;
步驟s2.8、計算增益:
kk=pk|k-1gt(r+gpk|k-1gt)-1(9)
步驟s2.9、更新狀態方程:
xk=xk|k-1+kkvk(10)
步驟s2.10、更新協方差陣:
pk=(i3×3-kkg)pk|k-1(11)。
所述的步驟s2.6中,更新衰減因子的方法具體包含以下步驟:
步驟s2.6.1、根據量測殘差實時調整衰減因子:
步驟s2.6.2、判斷衰減因子是否滿足lk≤ω,其中,ω是星敏運行角速度,若是,進行步驟s2.6.4,若否,進行步驟s2.6.3;
步驟s2.6.3、令lk=lk/10,進行步驟s2.6.2;
步驟s2.6.4、令λk=1+lk,若λk>λmax,取λk=λmax,λmax為設定的衰減因子最大值。
所述的步驟s3中,採用校準後的安裝關係四元數解算安裝矩陣的方法包含以下步驟:
步驟s3.1、獲得濾波校準後的安裝關係四元數的矢量部分:
步驟s3.2、解算安裝關係四元數的標量部分:
若q0<0,則否則
步驟s3.3、根據安裝關係四元數解算安裝矩陣:
轉換矩陣cba由下式解得:
本發明在無準確先驗信息的條件下,通過量測殘差序列給出濾波收斂判據,若收斂,衰減因子取1,並在線估計參數r,以避免收斂判據失效,若發散,實時解算衰減因子,調整當前拍在濾波過程中的權重,可有效解決因模型不準確導致的濾波性能下降甚至發散問題,本發明對安裝矩陣進行實時校準補償,不需存儲大量的量測信息,本發明直接對安裝關係四元數的矢部進行濾波,而不是三軸歐拉角,避免了反三角解算引入的誤差。
附圖說明
圖1是本發明提供的一種高精度星敏感器安裝矩陣在軌實時校準方法的流程圖。
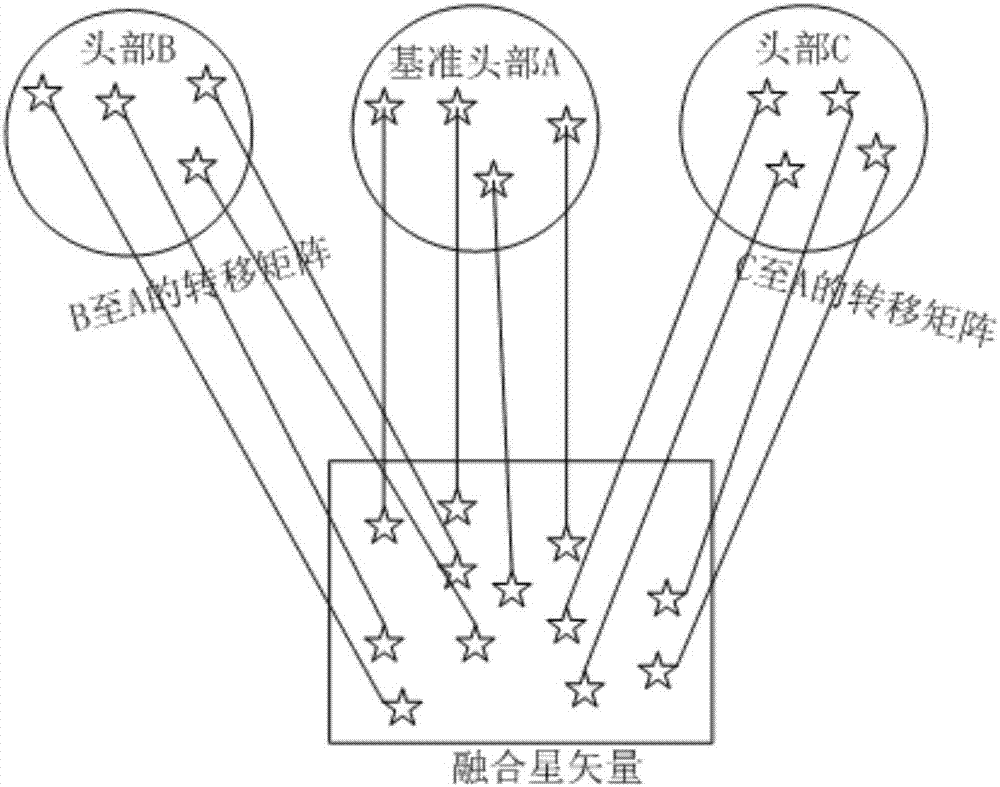
圖2是集中式星矢量融合示意圖。
圖3是對安裝關係四元數的矢量部分進行濾波校準的方法的流程圖。
圖4是參數q取不同值時的濾波結果。
圖5是更新衰減因子的流程圖。
圖6是採用校準後的安裝關係四元數解算安裝矩陣的流程圖。
具體實施方式
以下根據圖1~圖6,具體說明本發明的較佳實施例。
考慮到星敏感器在軌運行期間,受空間熱環境影響,結構發生變形,本發明基於四元數自適應卡爾曼濾波原理(以下簡稱q-akf),根據量測殘差實時調整當前拍在濾波中的權重,避免因模型不準導致濾波性能下降甚至發散的問題。
如圖1所示,本發明提供一種高精度星敏感器安裝矩陣在軌實時校準方法,包含以下步驟:
步驟s1、解算實測安裝關係四元數;
步驟s2、對安裝關係四元數的矢量部分進行濾波校準;
步驟s3、採用校準後的安裝關係四元數解算安裝矩陣。
如圖2所示,是集中式星矢量融合示意圖,在步驟s1中,選定探頭a為基準頭部,由實時輸出的探頭a,探頭b的四元數qa,qb解算探頭a和探頭b之間的實測安裝關係四元數qba:
由於結構變形量較小,在短時間內(10~20min以內)也可認為不變,因此可建立線性離散卡爾曼kalman濾波模型對安裝矩陣進行實時校準;
實測安裝關係四元數qba可表示為:
由於四元數的自由度為3,所以可只對其矢部濾波平滑;
取線性離散系統狀態為則系統方程為:
式中,k為離散時間;系統在時刻k的狀態矢量xk∈r3;yk∈r3為對應狀態的觀測矢量;wk~n(0,qk)為高斯分布的過程激勵噪聲;vk~n(0,rk)為高斯觀測噪聲;d為狀態轉移矩陣;g為觀測矩陣;由於建立的是線性模型,這裡d和g取為三階單位陣。
如圖3所示,所述的步驟s2中,對安裝關係四元數的矢量部分進行濾波校準的方法包含以下步驟:
步驟s2.1、輸入線性離散系統狀態量的初始值x0和協方差的初始值p0;
地面安裝裝調時得到安裝關係四元數初值,x0取其矢部,p0任取一量級小於單位陣的非零對角陣;
步驟s2.2、進行狀態一步預測:
xk|k-1=dxk-1(4)
步驟s2.3、計算量測殘差:
vk=yk-gxk|k-1(5)
步驟s2.4、判斷系統是否發散,若收斂判據成立,說明濾波正常,進行步驟s2.5,若收斂判據不成立,說明濾波發散,進行步驟s2.6;
所述的收斂判據為:
式中,γ為儲備係數(γ≥1),γ=1是最嚴格的收斂判據;
步驟s2.5、令衰減因子λk=1,同時,為了避免因參數r的取值不合理導致收斂判據失效,由量測殘差在線估計測量噪聲協方差r,進行步驟s2.7
式中,dk=(1-b)/(1-bk+1),b為遺忘因子,一般取0.95~0.99;
步驟s2.6、更新衰減因子,進行步驟s2.7;
步驟s2.7、一步預測協方差陣:
pk|k-1=d(λk*pk-1)dt+q(8)
式中,q為過程激勵噪聲協方差,該參數被用來表示狀態轉換矩陣與實際過程之間的誤差,因為無法直接觀測到過程信號,所以q的取值是很難確定的,無在軌數據支撐條件下,參數q無法準確估計,如圖4所示,在q取值接近於真實值和小於真實值的條件下,安裝矩陣三軸歐拉角總能收斂於參考值,q越接近於真實值收斂速度越快,當q過大時,融合姿態精度降低,所以q取值不宜過大;
步驟s2.8、計算增益:
kk=pk|k-1gt(r+gpk|k-1gt)-1(9)
式中,r為測量噪聲協方差,濾波器實際實現時,測量噪聲協方差一般可以觀測得到;
若星敏感器高頻誤差為expect_error角秒,測量噪聲協方差r可由下式求出:
步驟s2.9、更新狀態方程:
xk=xk|k-1+kkvk(10)
步驟s2.10、更新協方差陣:
pk=(i3×3-kkg)pk|k-1(11)。
如圖5所示,所述的步驟s2.6中,更新衰減因子的方法具體包含以下步驟:
步驟s2.6.1、根據量測殘差實時調整衰減因子:
步驟s2.6.2、判斷衰減因子是否滿足lk≤ω,其中,ω是星敏運行角速度(ω的單位為度/秒),若是,進行步驟s2.6.4,若否,進行步驟s2.6.3;
由於結構變形量與溫度變化量成正比,星敏運行角速率ω與溫度變化率成正比;
步驟s2.6.3、令lk=lk/10,進行步驟s2.6.2;
步驟s2.6.4、令λk=1+lk,若λk>λmax,取λk=λmax,λmax為設定的衰減因子最大值。
如圖6所示,所述的步驟s3中,採用校準後的安裝關係四元數解算安裝矩陣的方法包含以下步驟:
步驟s3.1、獲得濾波校準後的安裝關係四元數的矢量部分:
步驟s3.2、解算安裝關係四元數的標量部分:
若q0<0,則否則
步驟s3.3、根據安裝關係四元數解算安裝矩陣:
轉換矩陣cba可由下式解得:
本發明在無準確先驗信息的條件下,通過量測殘差序列給出濾波收斂判據,若收斂,衰減因子取1,並在線估計參數r,以避免收斂判據失效,若發散,實時解算衰減因子,調整當前拍在濾波過程中的權重,可有效解決因模型不準確導致的濾波性能下降甚至發散問題,本發明對安裝矩陣進行實時校準補償,不需存儲大量的量測信息,本發明直接對安裝關係四元數的矢部進行濾波,而不是三軸歐拉角,避免了反三角解算引入的誤差。
本發明可以在軌實時校準補償衛星的結構變形對探頭之間安裝矩陣的影響,具有很強的跟蹤能力和自適應性,用於多探頭星敏感器視場融合中的空間配準,提高融合姿態的精度。
儘管本發明的內容已經通過上述優選實施例作了詳細介紹,但應當認識到上述的描述不應被認為是對本發明的限制。在本領域技術人員閱讀了上述內容後,對於本發明的多種修改和替代都將是顯而易見的。因此,本發明的保護範圍應由所附的權利要求來限定。
