基於集成變量選擇型偏最小二乘回歸的軟測量方法與流程

2024-03-25 03:19:05

本發明涉及一種工業過程軟測量方法，尤其是涉及一種基於集成變量選擇型偏最小二乘回歸的軟測量方法。

背景技術：

在現代流程工業過程中，實時測量與監控產品的質量指標或其他某些能間接反映產品質量的指標是保證產品質量穩定性的最直接最簡單的途徑。相比於溫度、流量、壓力等容易測量的數據信息而言，這些能直接或間接反映產品質量信息的關鍵變量通常不是那麼容易獲取的。以液體產品的濃度為例，獲取濃度信息可通過在線分析儀實時測量，也可通過人工採集液體樣本進行離線分析，兩種手段各有優劣。在線分析儀雖能保證實時測量到的質量信息，但設備價格高昂，而且後期維護成本較高。離線分析手段所需設備價格低廉，但會造成嚴重的滯後，無法及時反映當前質量狀況。在這種背景下，軟測量技術應運而生，其基本思想在於：先利用生產過程歷史數據建立回歸模型，後在線利用與之相關的其他容易測量的變量(如溫度、壓力、流量等)，估計出該難以測量變量的數值以便實時監控產品的質量信息。

查閱已有的文獻與專利，可以發現實施軟測量的方法主要有：統計回歸法、神經網絡、支持向量回歸等。通常來講，在數據量非常充分以及非線性特性很強的條件下，利用神經網絡或支持向量回歸建立相應的軟測量模型，通常能取得較好的軟測量效果，但是這類方法在模型更新時會受限於訓練耗時大的問題。相比之下，統計回歸法所需的數據量較小，而且訓練時間很短，可較好的適應於模型更新，已越來越多地被應用在軟測量建模領域。偏最小二乘回歸(partialleastsquareregression，plsr)是最常用的統計回歸算法，各種改進舉措層出不窮。plsr算法旨在最大化輸入數據與輸出數據間的協方差，這裡的輸入數據通常是歷史資料庫中容易測量的數據(如溫度、壓力、流量等)，而輸出數據一般是直接或間接反映產品質量信息的測量數據(如濃度、成分比等)。然而，若是輸入數據中包含了很多與輸出不怎麼相關的幹擾變量的測量數據，plsr模型的回歸擬合精度會受到很大影響。由於軟測量方法通常針對的都是數據，直接通過數據剔除與輸出不相關的測量變量是非常困難的。若是依賴生產機理或操作人員經驗，那麼相應的plsr模型建立方法不具備通用性，而且對機理知識或經驗的正確性要求也非常高。

為此，科研文獻中出現了很多關於輸入數據變量選擇的方法以改進plsr模型的回歸精度，較常見的有回歸係數plsr法(β-plsr)、變量重要性plsr法(vip-plsr)、無益變量剔除plsr法(uve-plsr)等。不同的選擇方法揭示訓練數據不同的潛在特徵，但直至目前為止，還沒有文獻或專利直接證明哪種變量選擇方法無論針對何種工業對象的採樣數據始終是最佳的。針對某一個工業過程對象，確定哪種方法最合適實際上只有通過數據驗證才能知曉。考慮到現代流程工業的時變特性，環境以及設備狀態在不斷變化，相應採樣數據的特徵同樣是在變化的。可能某一段時間類採樣數據適合於某種變量選擇法，而另一時間段的採樣數據卻適合於使用另外一種變量選擇方法。因此，工業過程的時變特性給變量選擇型plsr方法的適用性提出了新的挑戰。因此，丞待設計出一種能應對這種數據變化特性的變量選擇型plsr軟測量方法。

技術實現要素：

本發明所要解決的主要技術問題是：在實際應用中，很難確定哪種變量選擇型plsr方法最適合於為當前數據建立軟測量模型。為此，本發明提供一種基於集成變量選擇型偏最小二乘回歸的軟測量方法。該方法首先同時使用多種變量選擇方法建立一個集成變量選擇型plsr模型。其次，在線實施軟測量時，利用該集成變量選擇型plsr模型計算得到多個輸出估計值。最後，通過加權計算得到最終的輸出估計值。

本發明解決上述技術問題所採用的技術方案為：一種基於集成變量選擇型偏最小二乘回歸的軟測量方法，包括以下步驟：

(1)利用集散控制系統收集工業生產過程中容易測量的數據組成軟測量模型的輸入訓練數據矩陣x∈rn×m，並對其進行標準化處理使各個過程變量的均值為0，標準差為1，得到新數據矩陣其中，n為訓練樣本數，m為過程測量變量數，r為實數集，rn×m表示n×m維的實數矩陣。

(2)採用離線分析手段獲取與輸入訓練數據x相對應的產品質量數據組成輸出訓練數據y∈rn×1，計算向量y的均值μ與標準差ε，並對其進行標準化處理得到新數據向量

(3)利用plsr算法建立輸入數據與輸出之間的回歸模型。

(4)分別實施β-plsr、vip-plsr、和uve-plsr方法，建立相應的軟測量模型。

(5)利用β-plsr、vip-plsr、和uve-plsr模型計算對應於輸出的估計值y1，y2，y3，並將其組成新的輸入矩陣z＝[y1，y2，y3]∈rn×3。

(6)再次利用plsr算法建立新輸入z與輸出之間的回歸模型其中，b＝[b1，b2，b3]∈r3×1為回歸係數向量，元素b1，b2，b3分別為β-plsr、vip-plsr、和uve-plsr模型的權值。

(7)收集新的容易測量的數據xt∈rm×l，並對其進行與x相同的標準化處理得到下標號t表示當前最新採樣時刻。

(8)分別利用β-plsr、vip-plsr、和uve-plsr模型計算得到t時刻的輸出估計值

(9)通過加權法計算t時刻的輸出估計值那麼t採樣時刻的質量指標的最終估計值為

與現有技術方法相比，本發明方法的主要優勢在於：同時建立了三個不同的變量加權型plsr軟測量模型，並通過加權的方式集成得到最終的輸出估計值，在線實施軟測量值時不再拘泥於單個的變量加權型plsr模型，而是採用多個軟測量模型集成的方式，巧妙地避免了確定哪種變量選擇型plsr方法最適合於為當前數據建立軟測量模型這一難題。此外，本發明方法通過plsr算法計算出來的回歸係數向量來對各模型輸出估計值進行適當加權，不僅不需要反覆驗證某個變量選擇方法的適用性，而且還可以進一步地提高軟測量模型的精度。可以說，本發明方法是在已有工作的基礎上，利用集成建模思路有效地提升變量選擇型plsr方法用於軟測量建模的適用性。

附圖說明

圖1為本發明方法的實施流程圖。

圖2為plsr算法迭代求取回歸模型的流程示意圖。

具體實施方式

下面結合附圖對本發明方法進行詳細的說明。

如圖1所示，本發明涉及了一種基於集成變量選擇型偏最小二乘回歸的軟測量方法，該方法的具體實施步驟如下所示：

步驟1：利用集散控制系統收集工業生產過程中容易測量的數據組成軟測量模型的輸入訓練數據矩陣x∈rn×m，並對其進行標準化處理使各個過程變量的均值為0，標準差為1，得到新數據矩陣其中，n為訓練樣本數，m為過程測量變量數，r為實數集，rn×m表示n×m維的實數矩陣。

步驟2：採用離線分析手段獲取與輸入訓練數據x相對應的產品質量數據組成輸出訓練數據y∈rn×l，計算向量y的均值μ與標準差ε，並對其進行標準化處理得到新向量

步驟3：利用plsr算法建立輸入數據與輸出之間的回歸模型，如下所示：

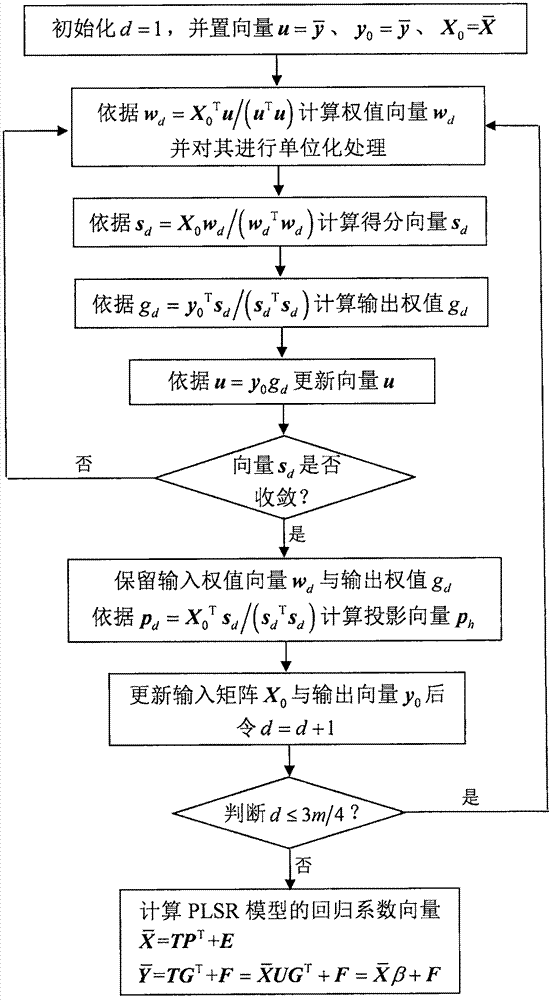
其中，為plsr模型中d個得分向量組成的矩陣，p∈rm×d與g∈rl×d分別為輸入與輸出數據的載荷矩陣，r∈rn×m與f∈rn×l分別為輸入與輸出數據的模型誤差，u∈rm×d為投影變換矩陣，β＝ugt為回歸係數向量，上標號t表示矩陣或向量的轉置。plsr算法的實施流程如圖2所示，具體操作步驟如下所示：

①初始化d＝1，並設置向量向量和矩陣

②依據公式wd＝x0tu/(utu)計算輸入權值向量wd，並用公式wd＝wd/||wd||單位化向量wd；

③依據公式sd＝x0wd/(wdtwd)計算得分向量sd；

④依據公式gd＝y0tsd/(sdtsd)計算輸出權值gd；

⑤依據公式u＝y0gd更新向量u；

⑥重複②～⑤直至sd收斂(即向量sd中各元素不再變化)；

⑦保留輸入權值向量wd與輸出權值gd，並依據公式pd＝x0tsd/(sdtsd)計算投影向量ph；

⑧依據如下兩式更新輸入矩陣x0與輸出向量y0：

x0＝x0-sdpdt(2)

y0＝y0-sdgd(3)

⑨令d＝d+1後，若d≤3m/4，重複②～⑧求解下一個wd、gd、和pd；若d＞3m/4，則執行⑩；

⑩將得到的所有輸入權值向量組成矩陣w＝[w1，w2，…，wd]、所有輸出權值向量組成行向量g＝[g1，g2，…，gd]、以及所有投影向量組成矩陣p＝[p1，p2，…，pd]，那麼plsr模型中的投影變換矩陣為u＝w(ptw)-1，d個得分向量組成的矩陣為回歸係數向量為β＝ugt＝w(ptw)-1gt。

步驟4：分別實施β-plsr、vip-plsr、和uve-plsr方法，建立相應的軟測量模型，具體的操作步驟如下所示：

實施β-plsr方法的具體步驟為：

①對回歸係數向量β中各元素求取絕對值得到新向量b，並計算向量b的均值，記為α；

②找出向量b中大於α的元素，並將相應的位置標號存放於位置標號集θ1中；

③根據記錄的位置標號θ1，從輸入數據矩陣中選取相應的列組成新的輸入數據矩陣x1；

④利用plsr算法建立輸入x1與輸出之間的回歸模型，並記錄相應的回歸係數向量β1；

實施vip-plsr方法的具體步驟為：

①初始化h＝1；

②根據如下所示公式計算輸入數據矩陣中第h個變量的重要性，即：

其中，wj，h表示向量wj中的第h個元素，符號||||表示計算向量的長度。

③判斷h＜m？若是，置h＝h+1後，若返回②計算下一個變量的重要性；若否，執行下一步驟④；

④找出向量v＝[v1，v2，…，vm]中大於1的元素，並將相應的位置標號存放於位置標號集θ2中；

⑤根據記錄的位置標號θ2，從輸入數據矩陣中選取相應的列組成新的輸入數據矩陣x2；

⑥利用plsr算法建立輸入x2與輸出之間的回歸模型，並記錄相應的回歸係數向量β2；

實施uve-plsr方法的具體步驟為：

①隨機產生一個n×m的數據矩陣n，矩陣n中各元素都是在區間[0，1]上均勻分布的隨機數；

②對矩陣n中各列進行標準化處理得到並將數據矩陣與組成新的輸入數據矩陣

③利用plsr算法建立輸入與輸出之間的回歸模型，並記錄相應的回歸係數向量

④將向量中前1至m個元素組成向量b1，第m+1至第2m個元素組成向量b2，並記錄向量b2中元素絕對值最大的數為δ；

⑤找出向量b1中絕對值大於δ的元素，並將相應的位置標號存放於位置標號集θ3中；

⑥根據記錄的位置標號θ3，從輸入數據矩陣中選取相應的列組成新的輸入數據矩陣x3；

⑦利用plsr算法建立輸入x3與輸出之間的回歸模型，並記錄相應的回歸係數向量β3；

步驟5：按照如下所示公式，分別利用β-plsr、vip-plsr、和uve-plsr模型中的回歸係數向量β1，β2，β3計算對應於輸出的估計值，分別記做y1，y2，y3，即：

yk＝xkβk(5)

上式中，下標號k＝1，2，3。並將其組成新的輸入矩陣z＝[y1，y2，y3]∈rn×3。

步驟6：再次利用plsr算法建立新輸入z與輸出之間的回歸模型其中，b＝[b1，b2，b3]∈r3×1為回歸係數向量，元素b1，b2，b3分別為β-plsr、vip-plsr、和uve-plsr模型的權值。值得指出的是，利用plsr算法建立z與之間的回歸模型的具體實施過程與步驟3相似，這裡不再贅述。

步驟7：收集新的容易測量的數據xt∈rm×l，並對其進行與x相同的標準化處理得到下標號t表示當前最新採樣時刻。

步驟8：依據位置標號集θ1，θ2，θ3分別從向量中選取相應的元素，對應組成新輸入向量x1，x2，x3；

步驟9：根據如下所示公式，利用β-plsr、vip-plsr、和uve-plsr模型中的回歸係數向量分別計算得到t時刻的輸出估計值即：

步驟10：通過加權法計算t時刻的輸出估計值那麼t採樣時刻的質量指標的最終估計值為

上述實施例只用來解釋本發明，而不是對本發明進行限制，在本發明的精神和權利要求的保護範圍內，對本發明做出的任何修改和改變，都落入本發明的保護範圍內。