峰值頻率檢測裝置、方法以及程序與流程
2023-11-01 17:30:30 1
本發明涉及功率譜最大的峰值頻率的檢測裝置、方法以及程序。
背景技術:
當將快速傅立葉轉換(FFT)的時間窗長度設為T0(s)、將採樣頻率設為fs(Hz)、將採樣數設為N(N是2的乘方的整數)時,則存在如下關係:
[算式1]
T0=N/fs。
時間窗長度的倒數f0(Hz)稱為頻率解析度,為如下關係:
[算式2]
f0=1/T0。
在通過FFT對信號波進行頻率分析的情況下,時間窗長度是進行FFT的信號波的時間長度,頻率解析度是信號波頻率的最小解析度,即為頻率的檢測精度。以下,也將該時間窗長度稱為「進行FFT的信號波的截取時間」、「進行FFT的信號波的時間」等。[算式2]的意思是:FFT的時間窗長度與頻率解析度呈互反關係。該互反關係在頻率解析度小的頻率處影響顯著。例如,如果需要0.01(Hz)的頻率解析度,則必須對其倒數的100(s)期間的信號波進行FFT。此外,如果進行FFT的信號波的時間是0.01(s),則只能得到其倒數100(Hz)的頻率解析度。
當利用FFT時,該互反關係有時成為制約,為了避免互反關係的制約,想盡了各種辦法。例如,可想到如下方法:在對接收的信號波進行FFT,求出構成在頻域出現的頻譜的峰值頻率時,將時間窗長度T0固定為預定值,對從所接收的信號波以間隔T0而不相互重疊的方式錯開並截取的多個期間分別應用FFT(即,多次應用FFT),將求得的多個峰值頻率取平均。在該方法中,有時也能以高於通過一次FFT求得的頻率解析度f0的解析度(細頻率間隔)計算出峰值頻率。但是,存在如下問題:如果增加FFT的操作次數,則進行FFT的信號波的截取時間隨著其次數增加而變長。
需要說明的是,當對數字數據串應用FFT時,對於提供給FFT的樣本數N,可得到0到N-1的被賦予固定的頻率間隔(等於頻率解析度(f0))下的振幅的值的功率譜。將這些功率譜中與最大值的功率譜對應的頻率稱為峰值頻率。最大值的功率譜能通過公知的方法確定,例如,如果將1到N/2的功率譜逐個進行比較則能夠確定。此時,如果在p點功率譜最大,則峰值頻率fpk為fpk=p×f0。
在專利文獻1中,對如下方法進行了說明:同時滿足頻率解析度小於等於12(Hz)、進行FFT的信號波的截取時間小於等於10(ms)(相當於水中的位置解析度7.5m),並求出峰值頻率(參照該專利文獻1的[0023]~[0026]、[0089]~[0090]。需要說明的是,在[0097]之後的數值例中,從輸入信號波的截取時間變為5(ms),但理由不明。)。當以頻率解析度12(Hz)優先時,根據[算式2],截取時間為1/12(Hz)=83.3(ms)。另一方面,在應用FFT的情況下,由於要求其樣本數N是2的乘方,因此,在該專利文獻1中,將信號截取時間設為相當於N=1024的102.4(ms)(參照該專利文獻1的[0055])。為了將進行FFT的輸入信號波的截取時間設為102.4(ms),由於以獲得實際的數據的時間5(ms)是不夠的,因此對不夠的量102.4-5=97.4(ms)期間的部分附加零值數據,將加入該零值數據所得的數據串(時間長度102.4(ms)的部分)進行FFT,求出峰值頻率(參照該專利文獻1的[0103])。
在該專利文獻1記載的方法中,由於進行FFT的數據串中所含的有效數據串只不過是整體的約1/10(根據該專利文獻1的[0103],約1/20),因此,當使施加於在輸入信號波是模擬信號波時通常應用的A/D轉換而得到的數位訊號波的數字帶通濾波器(在該專利文獻1的圖7中,數字BPF62)提高階數並且為窄帶時,通過數字帶通濾波器後的信號遲鈍,而且有效數據數量減少,因此必須減緩數字帶通濾波器的濾波特性。就是說,在該專利文獻1中,由於絲毫沒有認識到難以避免時間長度短的輸入信號波的情況下的由幹擾噪聲引起的負面影響這一潛在問題,因此,對那樣的潛在問題的解決方案也沒有任何啟示和教導。
此外,在該專利文獻1的情況下,在進行FFT的數位訊號波(數字數據串)中,由於僅在應用FFT時所要求的時間窗長度約1/10(或者,約1/20)的長度的部分存在實際的數據,因此不得不產生大量的功率譜。在應用FFT的實際的信號波中包含幹擾噪聲的情況下,由於在峰值頻率的周邊進一步出現多餘的頻譜,因此存在難以確定峰值頻率的可能性。
如此,當求取輸入信號的峰值頻率時,為了避免互反關係的制約而進行了各種嘗試,但尚未找到常規的解決方法。
現有技術文獻
專利文獻
專利文獻1:日本特開2012-247302號公報
技術實現要素:
發明所要解決的問題
本發明的目的在於提供一種裝置、方法以及程序,所述裝置、方法以及程序能避免通過FFT進行頻率分析時成為制約的、存在於頻率解析度(f0)與時間窗長度(T0)之間的f0=1/T0這一互反關係,能以所希望的頻率解析度和所希望的時間窗長度來檢測信號波的峰值頻率。
用於解決問題的方案
(1)用於達成上述目的的峰值頻率檢測裝置是檢測規定的頻帶(fcl~fch)中功率譜最大的峰值頻率的峰值頻率檢測裝置,具備:n次方部,對數字數據串的各元素取n次方(n是大於等於2的整數);FFT部,將與對根據採樣頻率fs、頻率解析度ftg、時間窗長度Ttg確定的N(N是2的乘方的整數)個取n次方後的採樣頻率fs的數字數據串進行快速傅立葉轉換所得的功率譜的最大值對應的頻率作為虛擬峰值頻率導出;以及1/n倍部,將對所述虛擬峰值頻率取1/n倍後的值作為數字數據串的峰值頻率輸出,所述峰值頻率檢測裝置滿足:
n≥1/(ftg×Ttg)
fs/(n×ftg)≤N≤fs×Ttg
fs>2×n×fch。
需要說明的是,在本說明書中,fcl~fch是指大於等於fcl小於等於fch。
當假定作為頻率分析的對象的信號波y是具有單一頻率f(Hz)的[算式3]所示的正弦函數時,y的n次方(n是大於等於2的正整數)以[算式4]以及[算式5]表示。在[算式4]中n是奇數,在[算式5]中n是偶數。
[算式3]
y=sin(2πft)
[算式4]
[算式5]
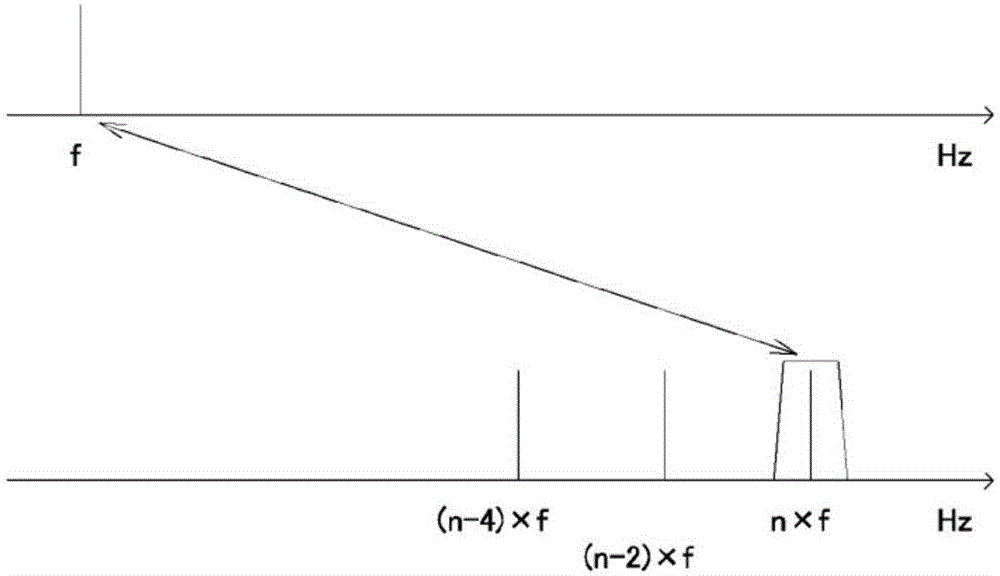
當對y取n次方(n=2,3,4,……)時,無論n是奇數還是偶數,[算式4]以及[算式5]都表示:出現頻率成分n×f,(n-2)×f,(n-4)×f,……。
因此,可以理解的是:如果能對y=sin(2πft)取n次方,並從此取n次方得到的信號波中提取頻率成分(n×f)的信號波,求出此信號波的峰值頻率,那麼如果對求得的頻率取1/n倍,則其與原信號波的頻率f對應。圖1示意性地表示了該關係。
在此,將使用於頻率分析的FFT的採樣頻率設為fs,將樣本數設為N。當將y=sin(2πft)進行該FFT並求取峰值頻率時,則該峰值頻率是f的計算值,此時的頻率解析度f0為:
[算式6]
f0=fs/N。
在此,當將頻率成分是(n×f)的正弦函數yn=sin(2πnft)進行具有與求出y的峰值頻率時相同值的fs和N的FFT並求取峰值頻率時,求得的yn的頻率fn』為(n×f)的計算值。在此,應該注意的是,該yn的頻率fn』是在與關於y的頻率解析度相同的頻率解析度f0的基礎上求得的。就是說,fn』的頻率解析度也是f0。因此,對fn』取1/n倍後的fn』/n是以頻率解析度f0/n求出y的頻率f。
因此,當將直接進行FFT求出y的頻率f時的頻率解析度設為f0,將時間窗長度設為T0,將根據yn求出y的頻率f時的頻率解析度設為fn,將時間窗長度設為Tn時,則如下關係成立:
[算式7]
fn=f0/n(n是大於等於2的整數)
[算式8]
Tn=T0
[算式9]
fn×Tn=(f0/n)×T0=1/n<1(n是大於等於2的整數)。
關於[算式9],在圖2中示出了n=2,3,4時和不進行乘方時的f0×T0=1的曲線圖。
當求取原信號波的峰值頻率時,頻率解析度ftg是用戶所希望的峰值頻率的頻率解析度。時間窗長度Ttg是用戶所希望的FFT的時間窗長度。ftg與Ttg可以獨立設定。
就是說,本發明是以滿足如下條件的方式對原信號波的峰值頻率進行計算的方法。
·峰值頻率的頻率解析度fn≤ftg
·FFT的時間窗長度Tn≤Ttg
為此,根據[算式9],需要滿足:
[算式10]
fn×Tn=1/n≤ftg×Ttg。
就是說,次方數n必須滿足:
[算式11]
n≥1/(ftg×Ttg)。
需要說明的是,n不限於2的乘方2,4,8,16,32,……,只要選自大於等於2的整數即可。因此,可以根據用途來選擇需要且足夠的最優值。即,根據本發明,能避免通過FFT進行頻率分析時成為制約的、存在於頻率解析度(f0)與時間窗長度(T0)之間的f0=1/T0這一互反關係,能以所希望的頻率解析度和所希望的時間窗長度來檢測信號波的峰值頻率。具體而言,即使在ftg×Ttg<1的範圍,也能以所希望的頻率解析度和所希望的時間窗長度來檢測信號波的峰值頻率。
如[算式9]所示,將對信號波取n次方後的數字數據串進行FFT的情況下的峰值頻率的頻率解析度fn、時間窗長度Tn有fn×Tn=1/n的關係,如果對此進行圖示,則如圖4所示。該圖4中所描繪的fn×Tn=1/n的曲線圖中的粗線部分為滿足ftg、Ttg要求的fn、Tn。
當將fn=ftg時的Tn設為Tmin時,則Tn的可取範圍為:
[算式12]
Tmin≤Tn≤Ttg。
另一方面,由於
[算式13]
ftg×Tmin=1/n
Tn=N/fs,
因此,
[算式14]
1/(n×ftg)≤N/fs≤Ttg。
在進行FFT的情況下,由於N必須是2的乘方,因此N的可取範圍為:
fs/(n×ftg)≤N≤fs×Ttg(N是2的乘方)。
假如在N不存在的情況下,增大n或增大fs、或者增大兩者,直至N存在。不過,根據FFT的採樣定理,必須滿足:
[算式15]
fs>2×n×fch。
在相應的N存在多個的情況下,無論採用哪個N都滿足所希望的頻率解析度ftg和所希望的時間窗長度Ttg。不過,N越小,FFT的計算量越少,因此通常最好採用最接近下式的N。
[算式16]
fs/(n×ftg)
如此,即使在ftg×Ttg<1的範圍,也能確定能以所希望的頻率解析度ftg、時間窗長度Ttg來檢測峰值頻率的次方數n、FFT的採樣頻率fs、FFT的樣本數N。需要說明的是,次方數n、fs、N的確定方法可以不按照上述過程。可以適當地應用數值反覆進行試錯直至滿足條件,或者製作簡單的程序來導出,使用什麼樣的方法都可以。
(2)用於達成上述目的的峰值頻率檢測裝置具備:第一數字帶通濾波器,提取所述規定的頻帶中所含的頻率的數字數據串,所述第一數字帶通濾波器的輸出可以輸入至所述n次方部。
當採用該構成時,由於能夠為了從包含各種頻率成分的信號中提取規定的頻帶的信號而簡化或省略前一階段的模擬濾波器,因此能縮小電路規模。
(3)用於達成上述目的的峰值頻率檢測裝置具備:間隔剔除部,將採樣頻率fis的數字數據串間隔剔除為1/r(r是大於等於2的整數),並將採樣頻率設為fs,所述間隔剔除部的輸出可以輸入至所述第一數字帶通濾波器。
當採用該構成時,即使在輸入至峰值頻率檢測裝置的數字數據串的採樣頻率大於fs的情況下,也能以所希望的頻率解析度ftg、時間窗長度Ttg來檢測峰值頻率。
(4)用於達成上述目的的峰值頻率檢測裝置具備:內插部,將接收數字數據串內插為g倍(g是大於等於2的整數),並將採樣頻率設為fs,所述內插部的輸出可以輸入至所述第一數字帶通濾波器。
當採用該構成時,即使在輸入至峰值頻率檢測裝置的數字數據串的採樣頻率小於fs的情況下,也能以所希望的頻率解析度ftg、時間窗長度Ttg來檢測峰值頻率。
(5)用於達成上述目的的峰值頻率檢測裝置具備:第二數字帶通濾波器,從取n次方後的N個所述數字數據串中提取第二頻帶中所含的數字數據串,由所述第二數字帶通濾波器提取的數字數據串被輸入至所述FFT部,所述第二頻帶可以是大致n×fcl~n×fch。
假設即使是僅具有單一頻率成分的數字數據串,當取n次方時,也具有多個頻率成分,因此在功率譜出現多個峰值,但所要檢測的峰值出現在與頻帶fcl~fch對應的n×fcl~n×fch。因此,通過提取n×fcl~n×fch的成分,能檢測規定的頻帶(fcl~fch)中功率譜最大的峰值頻率。需要說明的是,在能從多個峰值頻率中確定並選擇所要檢測的峰值頻率的情況下,也可以不使用第二數字帶通濾波器。
(6)用於達成上述目的的峰值頻率檢測裝置具備:間隔剔除部,將由所述第二數字帶通濾波器提取的數字數據串間隔剔除為1/r(r是大於等於2的整數),並將採樣頻率設為fs,所述間隔剔除部的輸出可以輸入至所述FFT部。
當採用該構成時,即使在輸入至峰值頻率檢測裝置的數字數據串的採樣頻率大於fs的情況下,也能以所希望的頻率解析度ftg、時間窗長度Ttg來檢測峰值頻率。
(7)在用於達成上述目的的峰值頻率檢測裝置中,具備:第一數字帶通濾波器,提取所述特定的頻帶中所含的頻率的數字數據串;第二數字帶通濾波器,從所述n次方部的輸出中提取第二頻帶中所含的數字數據串,所述第一數字帶通濾波器的輸出被輸入至所述n次方部,所述第二數字帶通濾波器的輸出被輸入至所述FFT部,所述第二頻帶可以是大致n×fcl~n×fch。
(8)用於達成上述目的的峰值頻率檢測裝置,代替所述n次方部,具備多重乘方部,所述多重乘方部具備k(k是大於等於2的整數)級乘方塊(j),所述乘方塊(j)具備:乘方部(j)(j=1,2,……,k),對所輸入的數字數據串取mj次方;以及數字帶通濾波器(j),從所述乘方部(j)的輸出中提取特定的頻帶fcl(j)~fch(j)的信號,可以是:
n=m1×m2×……×mk
fcl(j)≈(m1×m2×……×mj)×fcl
fch(j)≈m1×m2×……×mj)×fch。
在對數字數據串進行乘方的情況下,次方數越小,越能減少由乘方產生的多餘的頻率成分。多餘的頻率成分越少,越容易通過數字帶通濾波器來去除多餘的頻率成分。即,與能以一級的乘方部和第二數字帶通濾波器應對的次方數n的上限相比,能以將乘方部和數字帶通濾波器單元化並採用多級構成的方式應對的次方數n的上限更大。因此,通過採用該構成,能擴大可設定為次方數的n的範圍。
(9)用於達成上述目的的峰值頻率檢測裝置可以具備:操作部,受理用戶的指示;以及參數設定部,對根據所述指示的n、fs、N的至少任一個進行設定。
通過採用該構成,用戶無需以重複進行試錯的方式設定滿足下式的n、fs、N:
n≥1/(ftg×Ttg)
fs/(n×ftg)≤N≤fs×Ttg
fs>2×n×fch。
需要說明的是,權利要求所述各部的功能通過功能由構成自身確定的硬體資源、功能由程序確定的硬體資源、或它們的組合來實現。此外,這些各部的功能並不限於通過各自物理上相互獨立的硬體資源來實現。而且,本發明作為方法、作為電腦程式、作為電腦程式的記錄介質都成立。當然,此電腦程式的記錄介質既可以是磁記錄介質,也可以是光磁記錄介質,還可以是今後開發的任何記錄介質。
附圖說明
圖1是表示本發明的實施方式的頻譜的圖。
圖2是本發明的實施方式的曲線圖。
圖3是本發明的實施方式的框圖。
圖4是本發明的實施方式的曲線圖。
圖5是表示本發明的實施方式的頻譜的圖。
圖6是本發明的實施方式的框圖。
圖7是本發明的實施方式的波形圖。
圖8是本發明的實施方式的框圖。
圖9是本發明的實施方式的框圖。
圖10是本發明的實施方式的框圖。
圖11是本發明的實施方式的波形圖。
圖12是本發明的實施方式的波形圖。
圖13是本發明的實施方式的框圖。
圖14是本發明的實施方式的框圖。
圖15是本發明的實施方式的框圖。
圖16是本發明的實施方式的畫面構成圖。
具體實施方式
以下,參照附圖對本發明的實施方式進行說明。需要說明的是,將在各圖中對應的構成要素賦予相同的附圖標記,並省略重複的說明。
1、第一實施方式
在第一實施方式中,對峰值頻率檢測裝置和使用了該裝置的都卜勒測量儀進行說明,所述峰值頻率檢測裝置以滿足所希望的頻率解析度ftg和所希望的時間窗長度Ttg的方式對以採樣頻率fs進行了採樣的接收數字數據串的、由下限值fcl和上限值fch確定的頻帶fcl~fch中的峰值頻率f進行檢測。
如圖3所示,作為本發明的第一實施方式的峰值頻率檢測裝置1具備:第一數字帶通濾波器(BPF)部11、n次方部12、第二數字帶通濾波器(BPF)部13、FFT部14、以及1/n倍部15。
首先,對次方數n、使用於頻率分析的FFT的採樣頻率fs、使用於頻率分析的FFT的採樣數N的確定方法的過程進行說明。
(步驟1:確定次方數n)
首先,確定滿足n≥1/(ftg×Ttg)的條件的n(n是大於等於2的整數)。例如,將n設為滿足n≥1/(ftg×Ttg)的最小的整數,如果在後述的步驟3中N不存在,則可以使n增加1並重新計算,也可以從最初就設得較大。
(步驟2:選擇FFT的採樣頻率fs)
為了滿足採樣定理,以fs>2×n×fch的方式來選擇FFT的採樣頻率fs。
需要說明的是,在本實施方式中,輸入至峰值頻率檢測裝置1的數字數據串的採樣頻率為FFT的採樣頻率fs。在fs因電路上的制約等而不滿足上式的情況下,使用其他實施方式。
(步驟3:確定FFT的樣本數N)
接著,選擇滿足fs/(n×ftg)≤N≤fs×Ttg(N是2的乘方)的N。假如在N不存在的情況下,增大n或增大fs、或者增大兩者,直至N存在。不過,根據FFT的採樣定理,必須滿足:
fs>2×n×fch。
通過以上所說明的方法選擇的次方數n、fs、N設定於n次方部12以及FFT部14。此外,要檢測峰值頻率的頻帶的下限值fcl和上限值fch被設定為第一數字BPF11的截止頻率。此外,對於第二數字BPF13的截止頻率,設定要檢測峰值頻率的頻帶的下限值fcl和上限值fch的n倍的值。
(根據數字數據串計算峰值頻率)
當向設定了次方數n、fs、N的峰值頻率檢測裝置1輸入作為對象的數字數據串時,如下所述,以滿足所希望的頻率解析度ftg和所希望的時間窗長度Ttg的方式檢測出峰值頻率。
當作為對象的數字數據串輸入至峰值頻率檢測裝置1時,第一數字BPF11從數字數據串的大範圍的頻率成分中排除所設定的頻帶以外的多餘的直流成分、低頻成分、高頻成分,提取接近單一頻率f的頻率成分。
在作為要檢測峰值頻率的頻帶,fcl~fch過寬,其間存在多個大的功率譜的情況下,如圖5所示,較好的是:重新將fcl~fch設定得較窄,分數次求出峰值頻率。在圖5的例子中,fcl~fch表示最初的頻帶,f1、f2表示具有大功率譜的兩個頻率,fcl』~fch』表示變窄後的頻帶。需要說明的是,fcl』~fch』的間隔無需是固定的,如圖5所示,頻率越高,越可以擴大fcl』~fch』的間隔。
在此,將從第一數字BPF11通過後的數字數據串設為A(1):a0,a1,a2,…。在A(1)中,除了頻率f,還包含功率譜小的一些多餘的頻率成分。
接著,將該A(1)輸入n次方部12。在n次方部12中,將上述確定的n作為次方數對A(1)的各元素進行乘方。當將從n次方部12通過後的數字數據串設為B(n):b0,b1,b2,……時,則bi=(ai)n(i=0,1,2,3,4,……)。在B(n)中,還包含:頻率成分n×f,(n-2)×f,(n-4)×f,……這樣的功率譜小的多餘的低頻成分和高頻成分。
接著,將B(n)輸入第二數字BPF13,提取n×fcl~n×fch的頻帶的頻率成分。通過第二數字BPF13,能從B(n)的大範圍的頻率成分中排除多餘的低頻、高頻成分,並提取接近單一頻率的頻率成分。雖然第二數字BPF13的頻帶設成第一數字BPF11的頻帶的n倍的n×fcl~n×fch為好,但根據用途,稍微改變也沒有關係。將從第二數字BPF13通過後的數字數據串設為C(n):c0,c1,c2,……。在C(n)中,除了頻率n×f,還包含一些多餘的頻率成分。
在此,將輸入至峰值頻率檢測裝置1的數字數據串的採樣頻率fs設為fs>2×n×fch的理由是C(n)的頻帶的上限是n×fch。就是說,接收數字數據串的採樣頻率fs以滿足FFT的採樣定理為條件。
接著,將C(n)輸入FFT部14並計算出峰值頻率。在FFT部14中,以所設定的採樣頻率fs和樣本數N來對C(n)執行FFT,計算出峰值頻率。將從FFT部14輸出的峰值頻率設為(n×f』)。
接著,使從FFT部14輸出的峰值頻率(n×f』)通過1/n倍部15,求出f』。求得的f』為輸入至峰值頻率檢測裝置1的數字數據串的峰值頻率f的計算值。該f』是以滿足ftg、Ttg的方式計算出的。
如以上所說明,峰值頻率檢測裝置1能根據接收數字數據串,以所希望的頻率解析度ftg和所希望的時間窗長度Ttg來檢測峰值頻率。然後,由於峰值頻率檢測裝置1不進行近似計算,因此不存在計算出的峰值頻率的精度劣化。因此,能高精度地檢測峰值頻率。
圖6是表示組裝了峰值頻率檢測裝置1的都卜勒測量儀2的框圖。在都卜勒測量儀2中,具備:收發器21,其兼具向介質中發送信號波的功能和接收來自介質中的對象物的反射波的功能。收發器21介由收發切換電路22連接於發送電路23的輸出端和接收放大器24的輸入端。發送電路23生成發送頻率ftx的信號。在接收放大器24的輸出端設有將接收信號變頻為中間頻率信號的調製器25,本地振蕩頻率floc的信號從本地振蕩電路26供給至調製器25。調製器25的輸出、即中間頻率信號介由模擬濾波器27輸入至模擬/數字轉換器(A/D)28,從而以FFT所要求的採樣頻率被轉換為數位訊號。接著,該數位訊號輸入至峰值頻率檢測裝置1並通過FFT進行頻率分析,從峰值頻率檢測裝置1輸出峰值頻率。
在本實施例中,對在以下條件下檢測海水中的聲波的峰值頻率的方法進行說明。
海水中的聲波傳播速度C:1500m/s
發送頻率ftx:120kHz
本地發信頻率floc:137kHz
檢測最大速度(水平方向)V:15m/s
檢測速度精度(水平方向)V0:0.15m/s
檢測對象物的位置的精度(位置解析度)D0:7.5m
此外,設為聲波在相對於水平方向的傾斜方向(θ=60°)上進行信息收發。
在C>>V的情況下,都卜勒頻率fdop為:
[算式17]
由於檢測最大速度V是15m/s,因此:
[算式18]
都卜勒信號是120±1.2kHz的範圍,所觀測的頻帶的寬度Δfp為:
Δfp=2×1200Hz=2400Hz。
在此,中間頻率fmid設為floc-ftx=137-120=17kHz。
模擬濾波器27具有如下特性:
使fmid±(△fp/2)=17000±1200Hz的信號通過,在下一階段的A/D轉換器28不產生混疊(aliasing)。
由於檢測速度精度V0是0.15m/s,因此:
[算式19]
頻率解析度f0為12Hz。
由於檢測對象物的位置的精度(位置解析度)是7.5m,因此時間窗長度是作為往復7.5m的時間的、7.5×2/1500=10ms。
即使直接將模擬/數字轉換器(A/D)28的輸出進行FFT,也不能滿足該條件。其原因是,在頻率解析度是12Hz時,時間窗長度為1/12=83.3ms(>10ms),位置解析度為0.0833×1500/2=62.5m(>7.5m)。相反,當將時間窗長度設為10ms時,頻率解析度為1/0.01=100Hz(>12Hz)。
因此,通過具備n次方部12和1/n倍部15的峰值頻率檢測裝置1來求出峰值頻率。當將所希望的頻率解析度ftg設為12Hz,將所希望的時間窗長度Ttg設為10ms時,次方數n為:
n≥1/(ftg×Ttg)=1/(12×0.01)=8.3。在此,設為n=12。
接著,確定A/D轉換器28的採樣頻率fs。當第一數字BPF11的頻帶fcl~fch匹配17000±1200Hz時,fcl=15800Hz,fch=18200Hz。因此,A/D轉換器28的採樣頻率fs為:
fs>2×n×fch=2×12×18200=436800Hz,所以設為fs=510kHz。
根據fs/(n×ftg)≤N≤fs×Ttg,FFT的樣本數N是滿足510000Hz/(12×12Hz)=3541.7≤N≤510000Hz×0.01s=5100的2的乘方的整數。即,N=4096。
以這種方式確定採樣頻率fs和樣本數N,將從模擬/數字轉換器(A/D)28輸出的數字數據串輸入峰值頻率檢測裝置1。
需要說明的是,作為第一數字BPF11,例如,可以優選使用階數為8階且將截止頻率設定為fcl=15.8kHz、fch=18.2kHz的巴特沃斯型的IIR(Infinite impulse response:無限脈衝響應)濾波器。此外,作為第二數字BPF13,例如,可以優選使用階數為8階且將截止頻率設定為189.6kHz(12×fcl)以及218.4kHz(12×fch)的巴特沃斯型的IIR濾波器。
在此,將對象物的相對移動速度(水平方向)V設為V=10m/s,設為在相對於水平方向的傾斜方向(α=60°)上對聲波進行收發。
接收信號波的都卜勒頻率fdop為:
[算式20]
當將Sin{2π(17000+800)t}=Sin(2π17800t)假定為向採樣頻率510kHz的A/D轉換器28的輸入信號,製成偽數字數據串後,通過上述設定實際求取峰值頻率時,得到(12×f』)≈213662.1Hz。所求的f』為:f』=(12×f』)/12=213662.1/12≈17805.2Hz。f』是以滿足ftg的方式計算出的。實際上,對該數字數據串的測量誤差ε是ε=f』-fdop=17805.2-17800=5.2Hz,包括在±(ftg)/2=±6Hz以下。需要說明的是,由於頻率解析度f0時的峰值頻率為f0的間隔中最近的點,因此頻率解析度f0時的峰值頻率的誤差為±(f0/2)以下。
在本實施例中,將從第二數字BPF13輸出的數字數據串的實例在圖7中示出。在圖7中,T1是進行FFT的區間。T2是直至數字數據串的振幅穩定的區間。由於T1的元素數是4096個,因此T1的區間長度為4096/510000≈8.0ms,滿足所希望的時間窗長度Ttg=10ms。
需要說明的是,更優選將區間T2中振幅穩定後的數字數據串進行FFT。由於T2的元素數是約600個,因此T2的區間長度為600/510000≈1.2ms。即使是在這種情況下,由於將次方數n設定為較大的12,因此計算峰值頻率所需的數字數據串的時間長度是1.2+8.0=9.2ms,小於等於Ttg=10ms。需要說明的是,在本實施例中,即使將T2之後的4096個數字數據串進行FFT,計算結果也是f』≈17805.2Hz,得到相同值。
如此,通過增大次方數n,能輕鬆地滿足Ttg,增大第一數字BPF11、第二數字BPF13的階數使其陡峭,能抵抗外來噪聲。需要說明的是,可容易地理解的是:即使Ttg是5ms,通過增大次方數n,也能以所希望的頻率解析度ftg來進行頻率分析。
在此,對設置作為帶通濾波器的第一數字BPF11的理由進行說明。為了應用[算式4]以及[算式5],在取n次方之前,需要去除頻帶fcl~fch以外的多餘的直流成分、低頻成分、高頻成分。如果能通過模擬濾波器27來實現,則可以不需要第一數字BPF11。但是,這樣的模擬濾波器為高階且高精度,電路規模大,成本高。因此,模擬濾波器27採用在A/D轉換器28不產生混疊的程度的設計,頻帶fcl~fch的成分的提取採用能容易地實現高階且高精度的設計並且成本低的數字帶通濾波器才是上策。
2、第二實施方式
圖8是表示作為本發明的第二實施方式的峰值頻率檢測裝置3的構成的框圖。峰值頻率檢測裝置3為在峰值頻率檢測裝置1的第一數字BPF11之前追加有間隔剔除部16的構成。這是為了通過對A/D轉換後的數字數據串進行間隔剔除使其減少來降低採樣頻率。在輸入至峰值頻率檢測裝置3的數字數據串的採樣頻率fs高、次方數n和第一數字BPF11的截止頻率fch滿足fs>4×n×fch的情況下,優選應用第二實施方式。
在間隔剔除部16中,將數字數據串間隔剔除為1/r(r是大於等於2的整數),間隔剔除後的數字數據串為:
fs>2×n×fch。fs是間隔剔除後的採樣頻率。
對於間隔剔除為1/r,例如,以如下方式進行:將間隔剔除前的數字數據串設為P(1):p0,p1,p2,……,將間隔剔除後的數字數據串設為Q(1):q0,q1,q2,……時,進行qi=p(r×i)(i=0,1,2,3,4,……)。在r=2時,為q0=p0,q1=p2,q2=p4,q3=p6。
間隔剔除的方法可以是其他方法。例如,在r=2時,也可以採用q0=(p0+p1)/2,q1=(p2+p3)/2,q2=(p4+p5)/2,……等。
需要說明的是,在設為r=2時,不存在滿足fs/(n×ftg)≤N≤fs×Ttg(N是2的乘方)的N,也無法增大n的情況下,無法應用本實施例。該情況應用第一實施方式。
以下,對將本實施例的峰值頻率檢測裝置3應用於圖6所示的都卜勒測量儀2的情況進行說明。需要說明的是,下述數值數據以外所需的數值數據設為與第一實施方式的數值例相同。此外,為了簡化之後的說明,與第一實施方式相同,當將fs=510kHz的A/D轉換器28的採樣頻率設為10.2MHz時,輸入至間隔剔除部16的接收數字數據串的採樣頻率fis為10.2MHz。
在此,fis=10.2MHz>4×n×fch=4×12×18.2kHz=873.6kHz。另一方面,2×n×fch=2×12×18.2kHz=436.8kHz。因此,設為將接收數字數據間隔剔除為1/r=1/20。當將間隔剔除後的數字數據串的採樣頻率設為fs時,
fs=fis/r=10.2MHz/20=510kHz>436.8kHz。
當將間隔剔除前的數字數據串設為P(1):p0,p1,p2,……,將間隔剔除後的數字數據串設為Q(1):q0,q1,q2,……時,在間隔剔除部16中,進行q0=p0,q1=p20,q2=p40,q3=p60,……。
可以理解的是:該Q(1)與以採樣頻率fs=510kHz對輸入信號進行A/D轉換後的信號串同等。因此,FFT的採樣頻率fs為fs=510kHz。
與第一實施方式相同,在將y=sin(2π17800t)假定為向採樣頻率10.2MHz的A/D轉換器28的輸入信號,製成偽數據串後,以上述實施例的設定實際進行頻率分析的結果與第一實施方式的數值例相同,滿足ftg、Ttg。
3、第三實施方式
圖9是表示本發明的第三實施方式的峰值頻率檢測裝置4的構成的框圖。峰值頻率檢測裝置4為在第一實施方式的第二數字BPF13之後追加有間隔剔除部17的構成。對於第一數字BPF部11、n次方部12、第二數字BPF13,只不過是所輸入的數字數據的採樣頻率在第一實施方式中為fs而在此為fis,動作是相同的。在接收數字數據串的採樣頻率fs高、相對於次方數n和第一數字BPF11的截止頻率fch,fs>4×n×fch的情況下,為了削減計算量,一般應用第二實施方式為好。但是,即使是在本實施方式中,也能進行滿足所希望的時間窗長度ftg、所希望的時間窗長度Ttg的處理。
在間隔剔除部17中,在將接收數字數據串間隔剔除為1/r(r是大於等於2的整數),將間隔剔除後的數字數據串的採樣頻率設為fs時,
fs>2×n×fch。
間隔剔除後的數字數據串輸入至FFT部14,此後的處理與第一實施方式相同。
需要說明的是,在不滿足r≥2且fs/(n×ftg)≤N≤fs×Ttg(N是2的乘方)的情況下,無法應用本實施方式。該情況下,應用第一實施方式。
以下,對將本實施例的峰值頻率檢測裝置4應用於圖6所示的都卜勒測量儀2的情況進行說明。需要說明的是,下述數值數據以外所需的數值數據設為與第一實施方式的數值例相同。在A/D轉換器28的採樣頻率是10.2MHz的情況下,輸入至間隔剔除部17的接收數字數據串的採樣頻率fis為10.2MHz。
在此,fis=10.2MHz>4×n×fch=4×12×18.2kHz=873.6kHz。另一方面,2×n×fch=2×12×18.2kHz=436.8kHz。因此,設為將從第二數字BPF13通過後的數字數據間隔剔除為1/r=1/20。當將間隔剔除後的數字數據串的採樣頻率設為fs時,fs=fis/r=10.2MHz/20=510kHz>436.8kHz。FFT的採樣頻率fs為fs=510kHz。
與第一實施方式的數值例相同,在將y=sin(2π17800t)假定為向採樣頻率10.2MHz的A/D轉換器28的輸入信號,製成偽數字數據串後,以上述實施例的設定實際進行頻率分析的結果與第一實施方式的數值例相同,滿足ftg、Ttg。
4、第四實施方式
(以下,在申請時將段落號上調)圖10是表示作為本發明的第四實施方式的峰值頻率檢測裝置5的構成的框圖。峰值頻率檢測裝置5為在第一實施方式的數字BPF11之前追加有內插部18的構成。通過追加內插部18,能對A/D轉換後的數字數據串進行內插使其增加,由此提高採樣頻率。在輸入至峰值頻率檢測裝置5的數字數據串的採樣頻率fs低、相對於次方數n和第一數字BPF11的較高的截止頻率fch,2×fch<fs<2×n×fch的情況下,應用本實施方式。
在內插部18中,將接收數字數據串內插為g倍(g是大於等於2的整數),從而內插後的數字數據串的採樣頻率fs為fs>2×n×fch。例如,在將內插前的數字數據串設為U(1):u0,u1,u2,……,將內插後的數字數據串設為V(1):v0,v1,v2,……時,內插部18以如下方式進行內插:
vi=u0(i=0,1,2,3,……,(g-1))
vi=u1(i=g,g+1,g+2,g+3,……,(2g-1))
vi=u2(i=2g,2g+1,2g+2,2g+3,……,(3g-1))
……
在g=2時,v0=u0,v1=u0,v2=u1,v3=u1,v4=u2,v5=u2,……。內插的方法可以是其他方法。例如,在g=2時,也可以以如下方式進行內插:
v0=u0
v1=(u0+u1)/2
v2=u1
v3=(u1+u2)/2
v4=u2
v5=(u2+u3)/2
……
以下,對將本實施例的峰值頻率檢測裝置5應用於圖6所示的都卜勒測量儀2的情況進行說明。需要說明的是,下述數值數據以外所需的數值數據設為與第一實施方式的數值例相同。為了簡化說明,與第一實施方式相同,將fs=510kHz的A/D轉換器28的採樣頻率設為42.5kHz。此時,輸入至內插部18的接收數字數據串的採樣頻率fis為42.5kHz。該情況下,由於:
2×fch=2×18.2kHz=36.4kHz
2×n×fch=2×12×18.2kHz=436.8kHz
2×fch<fis<2×n×fch
因此應用本實施方式。
為了將接收數字數據串的採樣頻率擴大為大於等於436.8kHz,設成內插為g=12倍。當將內插後的數字數據串的採樣頻率設為fs時,
fs=fis×g=42.5kHz×12=510kHz>436.8kHz。
在將內插前的數字數據串設為U(1):u0,u1,u2,……,將內插後的數字數據串設為V(1):v0,v1,v2,……時,內插部18以如下方式進行內插:
v0~v11=u0
v12~v23=u1
v24~v35=u2
v36~v47=u3
……
當對內插後的數字數據串V(1)的例子進行圖示時,如圖11所示,呈階梯狀。圖11是將y=sin(2π17000t)假定為向採樣頻率42.5kHz的A/D轉換器28的輸入信號,在製成偽數字數據串後進行內插的例子。該V(1)的採樣頻率fs為510kHz。因此,此後的處理與圖10的構成的情況相同,將V(1)視為向第一數字BPF11輸入的採樣頻率fs的接收數字數據串,只要以相同的方法進行頻率分析即可。
與第一實施方式的數值例相同,將y=sin(2π17800t)假定為向採樣頻率42.5kHz的A/D轉換器28的輸入信號,在製成偽數字數據串後,以上述實施例的設定實際進行頻率分析的結果與第一實施方式的數值例相同,滿足ftg、Ttg。
在此,參照圖12,對將n次方部12之前的數字濾波器設為作為帶通濾波器的數字帶通濾波器的理由進行說明。
圖12A是向A/D轉換器28的輸入信號,設為:
y=sin(2π17000t)+2。
就是說,設為:殘留有未被模擬濾波器濾淨的直流成分2的、振幅1、頻率17kHz的sin波形。以採樣頻率為17kHz的2.5倍的42.5kHz對該輸入信號進行A/D轉換,其相當於輸入至峰值頻率檢測裝置1的數字數據串。
通過內插部18將該數字數據串擴大為12倍。圖12B是從內插部18輸出的數字數據串的例子。該數字數據串的採樣頻率變為相當於12×42.5kHz=510kHz。
圖12C是在使用了階數為8階且將截止頻率設定為fcl=15.8kHz、fch=18.2kHz的巴特沃斯型的IIR濾波器的情況下,從第一數字BPF部11輸出的數字數據串。第一數字BPF部11的輸出被消除了從內插部18輸出的多餘的直流成分、多餘的低頻成分、多餘的高頻成分,收斂後的波形成為接近sin波形的波形。
如此,如果預先通過第一數字BPF部11來限制頻帶,則在接下來的n次方部12取n次方時,能抑制[算式4]、[算式5]以外的頻率成分的產生。即,在n次方部12的前一階段具備數字帶通濾波器,由此即使數字數據串含有多餘的頻率成分也能應對。因此,能使前一階段的模擬濾波器27的性能要求降低至在下一階段的A/D轉換器28不產生混疊的程度,也能使A/D轉換器28的採樣頻率降低,因此能削減電路的規模和成本。
需要說明的是,截止頻率fcl、fch的數字帶通濾波器也可以採用將截止頻率fcl的數字高通濾波器與截止頻率fch的數字低通濾波器進行組合的構成。
5、第五實施方式
圖13是表示作為本發明的第五實施方式的峰值頻率檢測裝置6的構成的框圖。峰值頻率檢測裝置6是將第一實施方式的n次方部12和第二數字BPF13替換為多重乘方部19的裝置。
如圖14所示,多重乘方部19按照k級(k是大於等於2的整數)序號順序級聯有乘方塊(j),該乘方塊(j)包括:乘方部(j)(j=1,2,3,……,k),對數字數據串取mj次方(mj是大於等於2的整數);以及數字帶通濾波器(j)(BPF(j)),從乘方部(j)的輸出中提取特定的頻帶fcl(j)~fch(j)的信號。
乘方塊(j)的乘方部(j)的次方數mj以如下方式進行選擇:關於替換前的n次方部的次方數n,
n=m1×m2×……×mk成立。
此外,設定為:
fcl(j)≈(m1×m2×……×mj)×fcl
fch(j)≈(m1×m2×……×mj)×fch
在次方數mj是偶數的情況下,根據[算式5],當對y取mj次方時,產生直流成分。因此,需要數字BPF(j)能消除直流成分。
根據[算式4]、[算式5]可知:在對sin(2πft)取m次方的情況下,如果減小次方數m,則能減少所產生的小於等於(m-2)×f的頻率成分的數量。因此,更容易通過其後的數字BPF來抑制所需頻帶以外的頻率成分。因此,當應用本實施方式時,能應對至更高的次方數n。作為目標,在n次方部的次方數n大於16的情況下,考慮採用本實施方式為好。
在本實施方式中,與第一實施方式相同,也滿足所希望的頻率解析度ftg和所希望的時間窗長度Ttg。此外,在本實施方式中,未進行近似計算,因此也不存在所計算的峰值頻率的精度劣化。
在本實施方式中,由於將乘方部和第二數字BPF部設為多級構成,因此與第一實施方式相比計算量增加。但是,能夠滿足所希望的頻率解析度ftg和所希望的時間窗長度Ttg並且無精度劣化地對峰值頻率進行計算直至更高的次方數n這一優點彌補這些負面影響綽綽有餘。
以下,對將本實施例的峰值頻率檢測裝置6應用於圖6所示的都卜勒測量儀2的情況進行說明。需要說明的是,下述數值數據以外所需的數值數據設為與第一實施方式的數值例相同。為了簡化之後的說明,與第一實施方式相同,設為:n=12、fs=510kHz、N=4096、n=m1×m2。此外,設為:m1=4,m2=3。
在將y=sin(2π17800t)假定為向採樣頻率510kHz的A/D轉換器28的輸入信號並製成偽數字數據串後,向第一數字BPF11輸入,將第一數字BPF11的輸出設為A(1):a0,a1,a2,……。
在乘方部(1),對A(1)的各元素取4次方,將從乘方部(1)通過後的數字數據串設為B(4):b0,b1,b2,……。即,bi=(ai)4(i=0,1,2,3,4,……)。
使該B(4)從數字BPF(1)通過,並將從數字BPF(1)數字通過後的數字數據串設為C(4):c0,c1,c2,……。數字BPF(1)設為階數為8階且截止頻率63.2kHz(4×fcl)、72.8kHz(4×fch)的巴特沃斯型的IIR濾波器。
接著,在乘方部(2),對C(4)的各元素取3次方,將從乘方部(2)通過後的數字數據串設為D(12):d0,d1,d2,……。即,di=(ci)3(i=0,1,2,3,4,……)。
使該D(12)從數字BPF(2)通過,並將從數字BPF(2)通過後的數字數據串設為E(12):e0,e1,e2,……。數字BPF(2)設為階數為8階且截止頻率189.6kHz(4×3×fcl)、218.4kHz(4×3×fch)的巴特沃斯型的IIR濾波器。
關於該E(12),當以樣本頻率fs=510kHz、樣本數N=4096的FFT來求取頻率時,得出(12×f』)≈213662.1Hz。所求的f』為:f』=(12×f』)/12≈17805.2Hz。f』是以滿足ftg的方式計算出的。實際上,在此的相對於理論值f=17800Hz的誤差ε是:ε=f』-f=17805.2-17800=5.2Hz,包括在±(ftg)/2=±12/2=±6Hz。
此外,與第一實施方式相同,時間窗長度也是N/fs=4096/510kHz=8.0ms<Ttg=10ms,滿足所希望的時間窗長度Ttg。
6、第六實施方式
可以在此前所說明的峰值頻率檢測裝置1、3~6追加參數設定部。圖15是表示在第一實施方式的峰值頻率檢測裝置1追加了參數設定部20的構成的框圖。參數設定部20是具備處理器、存儲器、輸入輸出機構的計算機,根據使用了未圖示的鍵盤、滑鼠、觸控螢幕顯示器等未圖示的操作部的用戶的輸入,在峰值頻率檢測裝置1、3~6設定參數的值。參數如此前所說明,如下:
接收數字數據串的採樣頻率fis
數字數據串的採樣頻率fs
所希望的頻率解析度ftg
所希望的時間窗長度Ttg
n次方部的次方數n(n是大於等於2的整數)
第一數字BPF的頻帶大致fcl~fch(fcl<fch)
第二數字BPF的頻帶大致n×fcl~n×fch
FFT的採樣頻率fs
FFT的採樣數N
參數設定部20既可以將所述全部參數的數值與用戶可選擇的輸入值對應地預先存儲在存儲器中,並根據用戶的輸入值來進行設定,也可以將一部分參數的數值與用戶可選擇的輸入值對應地預先存儲在存儲器中,並根據用戶的輸入來進行設定,剩餘的參數根據所輸入的數值由處理器通過計算求出。
在本實施方式中,對用作調音輔助裝置的峰值頻率檢測裝置進行說明,所述調音輔助裝置使用戶僅輸入與頻率對應的音階序號,根據所輸入的音階序號從存儲器取得全部參數的數值並進行設定。即,參數設定部20從存儲器取得與音階序號1~88中任一個的輸入對應的參數的數值並進行設定。圖16是輸入音階序號狀態下的觸控螢幕顯示器的畫面構成圖的一個例子。全部參數的數值事先根據音階序號P全部確定並存儲在非易失性存儲器中。音階序號與平均律鋼琴的琴鍵對應,音階序號1與最低音的頻率對應,音階序號88與最高音的頻率對應。即,對於與音階序號P對應的頻率fp,由下述[算式21]確定的值被預先存儲在非易失性存儲器中。
[算式21]
然後,例如,相對於P=49(fp=442Hz)的各參數的數值以如下方式確定。
[算式22]
fs=24kHz
Ttg==(1/0.510913481)/10=0.195727855s
n=16
n×fc1=16×fc1=6870.673888Hz
n×fch=16×fch=7279·225418Hz
N=4096
需要說明的是,ftg是相當於fp的2音分(cent)的量的頻率。眾所周知,音分值是將兩個音之間的頻率比以對數形式表示的值,100音分相當於平均律12音階的半音。Ttg是時間窗長度(1/ftg)的1/10。fcl是fp的50音分下的頻率。fch是fp的50音分上的頻率。N必須是fs/(n×ftg)=24000/(16×0.5109)≈2936~fs×Ttg=24000×0.1957≈4697之間的2的乘方的整數。
如上所述,如果事先確定,參數設定部20就能根據音階序號P的輸入來設定全部參數的數值。通過使用如此設定的參數,能計算接收數字數據串的峰值頻率。需要說明的是,向峰值頻率檢測裝置1輸入的數字數據串既可以通過未圖示的話筒、A/D轉換器實時地依次輸入至峰值頻率檢測裝置1,也可以存儲於存儲器。
在設為P=49(fp=442Hz),並製成以採樣頻率24kHz對y=sin(2π442t)進行採樣的偽數字數據串後,實際進行頻率分析的結果是得到16×f』≈7072.2656Hz。所求的f』為f』=(16×f』)/16≈442.0166Hz。求得的峰值頻率的頻率解析度滿足所希望的頻率解析度ftg。實際上,在此的相對於理論值f=442Hz的誤差ε是ε=f』-f=442.0166-442=0.0166Hz,包括在±(ftg/2)=±0.5109/2≈±0.255Hz。此外,時間窗長度是N/fs=4096/24kHz=0.171s,滿足所希望的時間窗長度Ttg=0.195s。需要說明的是,求得的峰值頻率的輸出形式可以是單位Hz,也可以是相對於fp=442Hz的音分值(+0.065音分)。
7、效果
根據以上所說明的本發明的實施方式,能避免通過FFT進行頻率分析時成為制約的、存在於頻率解析度(f0)與時間窗長度(T0)之間的f0=1/T0這一互反關係的問題,能以所希望的頻率解析度ftg和所希望的時間窗長度Ttg來檢測信號波的峰值頻率。如果接收數字數據串的採樣頻率大於等於2×fch,則能計算峰值頻率。然後,由於無需進行近似計算、曲線擬合、取平均等處理,因此不存在峰值頻率的計算精度的劣化。
此外,即使在輸入信號包含多餘的頻帶的成分(直流成分、低頻成分,高頻成分)、或者S/N比差、或者幾乎沒有振幅的情況下,由於通過第一數字BPF、第二數字BPF來提取計算峰值頻率所需的頻帶的頻率成分,因此能毫無問題地計算出峰值頻率。因此,能降低峰值頻率檢測裝置的前一階段的硬體的要求規格,能謀求小型化、降低成本。具體而言,例如,相對於第一數字BPF的截止頻率fch,如果輸入信號的採樣頻率大於等於2×fch,則能計算峰值頻率,因此能降低前一階段的模擬濾波器、A/D轉換器等硬體的要求規格。此外,如果設定於乘方部的次方數n設定得較大,則能提高數字帶通濾波器的階數使其陡峭,抵抗外來噪聲。
8、其他實施方式
需要說明的是,本發明的技術範圍並不限定於上述實施例,在不脫離本發明主旨的範圍內可以進行各種變更。
例如,雖然舉例示出了IIR、巴特沃斯型、8階的數字BPF,但也可適當使用其他形式的數字BPF。例如,作為能優選使用的例子,可列舉出FIR(Finite impulse response:有限脈衝響應)、切比雪夫型等。階數也不限於8階。此外,截止頻率也是根據情況擴大或縮小提取範圍即可。此外,如果輸入信號是以0為中心振蕩的、幾乎沒有諧波成分的信號(就是說,接近單一頻率的sin曲線的信號),則可以將第一數字BPF設為低通濾波器。
此外,以反射回波中的都卜勒頻率的檢測、向調音輔助裝置的應用為例對本發明進行了說明,但本發明的應用範圍不限於此。一般情況下,本發明能廣泛應用於通過FFT進行信號波的峰值頻率的檢測的用途。
此外,上述實施方式的各功能部可以通過一個或多個LSI(Large Scale Integration:大規模集成電路)來實現,此外,多個功能部可以通過一個LSI來實現。此外,作為集成化的方法並不限定於LSI,也可以通過專用電路或通用處理器來實現。而且,可以在LSI製造後,利用可編程的FPGA(Field Programmable Gate Array:現場可編程門陣列)、可重新構成LSI內部的電路元件的連接或設定的可重構處理器(Reconfigurable Processor)。此外,如果通過半導體技術的進步或派生的其他技術,出現替代LSI的集成電路化的技術,當然也可以使用此技術來進行功能塊的集成化。
附圖標記說明:
1 峰值頻率檢測裝置
2 都卜勒測量儀
3 峰值頻率檢測裝置
4 峰值頻率檢測裝置
5 峰值頻率檢測裝置
6 峰值頻率檢測裝置
11 第一數字BPF部
12 n次方部
13 第二數字BPF部
14 FFT部
15 1/n倍部
16 間隔剔除部
17 間隔剔除部
18 內插部
19 多重乘方部
20 參數設定部
21 收發器
22 收發切換電路
23 發送電路
24 接收放大器
25 調製器
26 本地振蕩電路
27 模擬濾波器
28 A/D轉換器
