基於校驗矩陣的編解碼方法和裝置與流程

2023-10-11 13:53:54 1

本發明涉及通信技術領域，特別是涉及基於校驗矩陣的編碼方法和裝置以及基於校驗矩陣的解碼方法和裝置。

背景技術：

在數據通過通信鏈路傳輸的過程中，由於存在例如噪聲的幹擾因素，接收端接收到的數據存在一些錯誤的信息。為了實現數據的可靠傳輸，可以採用前向糾錯(Forward Error Correction，簡稱FEC)技術，以使得接收端能夠識別出接收到的錯誤信息。作為FEC技術的一種具體實現方式，低密度奇偶校驗碼(Low Density Parity Check Code，簡稱LDPC Code或LDPC碼)不但具有良好的理論性能而且也適於硬體實現。具體地，LDPC碼的理論性能是，LDPC不僅幾乎適用於所有的信道而且還能夠接近於香農限。LDPC碼適於硬體實現的原因在於，LDPC碼不僅解碼複雜度低，而且可並行實現。基於此，LDPC碼已被廣泛應用於多種通信協議中，如衛星數字視頻廣播DVB-S.2、寬帶無線接入協議IEEE802.16e以及乙太網規範10GBASE-T。

基於LDPC碼實現的數據傳輸具體包括如下步驟：當需要傳輸數據時，先採用預先構造的LDPC校驗矩陣對數據進行編碼從而得到編碼數據。然後，通過實際鏈路對編碼數據進行傳輸。接收端接收到編碼數據後，採用預先構造的LDPC校驗矩陣對編碼數據進行解碼從而得到所述數據。

在現有技術中，已經出現了一些能夠用於編碼和解碼的LDPC校驗矩陣。例如，一種現有的LDPC校驗矩陣H如下所示：

其中，LDPC校驗矩陣H由J個子矩陣H1、H2、……、Hj組成。LDPC校驗矩陣H是m×n維矩陣。子矩陣H1～Hj均是(m/J)×n維矩陣。在矩陣H 中，每行中元素「1」的數量為L，每列中元素「1」的數量為J。在子矩陣H1中，每行中元素「1」的數量為L，每列中元素「1」的數量為J，每行中的L元素「1」是連續的。子矩陣H2～Hj是分別對子矩陣H1進行列置換得到的。

需要說明的是，以LDPC校驗矩陣各行表示的校驗方程作為校驗節點，以LDPC校驗矩陣各列表示的變量作為變量節點，可以形成LDPC校驗矩陣的泰納圖(Tanner Graph，簡稱TG)，該TG的圍長(girth)表示該TG最短環的長度。發明人經過研究發現，現有技術中LDPC校驗矩陣對應的TG的圍長為4。當圍長等於4時，LDPC碼性能較低。具體來說，當傳輸中的LDPC碼的信噪比較低時，對接收到的LDPC碼進行解碼得到的數據的誤碼率較高。

技術實現要素：

本發明實施例提供一種基於校驗矩陣的編碼或者解碼方法，以及相關裝置，以解決現有技術中由於難以避免LDPC校驗矩陣的TG的圍長等於4而導致的LDPC碼性能較低的技術問題。

第一方面，本發明實施例提供了一種基於校驗矩陣的編碼方法，包括：

編碼器獲取數據；以及

所述編碼器通過利用LDPC校驗矩陣對所述數據進行編碼，生成編碼數據，所述LDPC校驗矩陣是基於矩陣H生成的，在矩陣H中，每行中元素「1」的數量為L，每列中元素「1」的數量為3，矩陣H為m×n維的矩陣；

m/3＝k×L且k為正整數，矩陣H由矩陣H1、矩陣H2和矩陣H3組成，矩陣H1構成矩陣H的第1行至第m/3行，矩陣H2構成矩陣H的第m/3+1行至第2m/3行，矩陣H3構成矩陣H的第2m/3+1行至第m行，矩陣H1、矩陣H2和矩陣H3均為(k×L)×(k×L2)維的矩陣；

其中，

在矩陣H1中，每行中元素「1」的數量等於L，每列中元素「1」的 數量等於1，每行中的L個元素「1」是連續的；

在矩陣H2中，每行中元素「1」的數量等於L，每列中元素「1」的數量等於1，矩陣H2由L個矩陣H4組成，矩陣H4為(k×L)×(k×L)維的對角陣，矩陣H4的主對角線上的元素都是「1」；

在矩陣H3中，每行中的元素「1」的數量為L，每列中的元素「1」的數量為1，矩陣H3包括k個矩陣H5，矩陣H5包括L個矩陣H6，矩陣H5為L×L2維的矩陣，矩陣H6為L×L維的對角陣，矩陣H6的主對角線上的元素都是「1」；

在矩陣H3中，所述k個矩陣H5之外的元素均為「0」，所述k個矩陣H5中第i個矩陣等於矩陣H3中第(i-1)×L+1行至i×L行與第(i-1)×L2+1列至第i×L2列對應的矩陣，i的取值範圍為1至k中的所有整數；

或者，

m/3＝k×L+r且k為正整數、r為1至L-1範圍內的正整數，矩陣H由矩陣H1』、矩陣H2』和矩陣H3』組成，矩陣H1』構成矩陣H的第1行至第m/3行，矩陣H2』構成矩陣H的第m/3+1行至第2m/3行，矩陣H3』構成矩陣H的第2m/3+1行至第m行，矩陣H1』、矩陣H2』和矩陣H3』均為(k×L+r)×(k×L2+r×L)維的矩陣；

其中，

在矩陣H1』中，每行中元素「1」的數量等於L，每列中元素「1」的 數量等於1，每行中的L個元素「1」是連續的；

在矩陣H2』中，每行中元素「1」的數量等於L，每列中元素「1」的數量等於1，矩陣H2』由L個矩陣H4』組成，矩陣H4』為(k×L+r)×(k×L+r)維的對角陣，矩陣H4』的主對角線上的元素都是「1」；

矩陣H3』是將矩陣H5』中第k×L2+b×L+c列與第b×L2+(c-1)×L+c列進行位置互換而得到的，b的取值範圍為0至r-1內的所有整數，c的取值範圍為1至L內的所有整數；

矩陣H5』中第1行至k×L行與第1列至k×L2列對應的矩陣等於矩陣H6』，矩陣H5』中第k×L+1行至第k×L+r行與第k×L2+1列至k×L2+r×L列對應的矩陣等於矩陣H7』，矩陣H5』中矩陣H6』和矩陣H7』之外的元素均為「0」；

矩陣H6』為(k×L)×(k×L2)維的矩陣，矩陣H7』為r×(r×L)維的矩陣，矩陣H6』等於矩陣H3，在矩陣H7』中，每行中元素「1」的數量為L，每列中元素「1」的數量等於1，每行的L個元素「1」是連續的。

在第一方面的第一種可能的實現方式中，所述LDPC校驗矩陣為矩陣H。

在第一方面的第二種可能的實現方式中，所述LDPC校驗矩陣是對矩陣H進行行置換和/或列置換而得到的。

第二方面，本發明實施例提供了一種基於校驗矩陣的解碼方法，包括：

解碼器獲取編碼數據；以及

所述解碼器通過利用LDPC校驗矩陣對所述編碼數據進行解碼，生成數據，所述LDPC校驗矩陣是基於矩陣H生成的，在矩陣H中，每行中元素「1」 的數量為L，每列中元素「1」的數量為3，矩陣H為m×n維的矩陣；

m/3＝k×L且k為正整數，矩陣H由矩陣H1、矩陣H2和矩陣H3組成，矩陣H1構成矩陣H的第1行至第m/3行，矩陣H2構成矩陣H的第m/3+1行至第2m/3行，矩陣H3構成矩陣H的第2m/3+1行至第m行，矩陣H1、矩陣H2和矩陣H3均為(k×L)×(k×L2)維的矩陣；

其中，

在矩陣H1中，每行中元素「1」的數量等於L，每列中元素「1」的數量等於1，每行中的L個元素「1」是連續的；

在矩陣H2中，每行中元素「1」的數量等於L，每列中元素「1」的數量等於1，矩陣H2由L個矩陣H4組成，矩陣H4為(k×L)×(k×L)維的對角陣，矩陣H4的主對角線上的元素都是「1」；

在矩陣H3中，每行中的元素「1」的數量為L，每列中的元素「1」的數量為1，矩陣H3包括k個矩陣H5，矩陣H5包括L個矩陣H6，矩陣H5為L×L2維的矩陣，矩陣H6為L×L維的對角陣，矩陣H6的主對角線上的元素都是「1」；

在矩陣H3中，所述k個矩陣H5之外的元素均為「0」，所述k個矩陣H5中第i個矩陣等於矩陣H3中第(i-1)×L+1行至i×L行與第(i-1)×L2+1列至第i×L2列對應的矩陣，i的取值範圍為1至k中的所有整數；

或者，

m/3＝k×L+r且k為正整數、r為1至L-1範圍內的正整數，矩陣H由矩陣H1』、矩陣H2』和矩陣H3』組成，矩陣H1』構成矩陣H的第1行至第m/3行，矩陣H2』構成矩陣H的第m/3+1行至第2m/3行，矩陣H3』構成矩陣H的第2m/3+1行至第m行，矩陣H1』、矩陣H2』和矩陣H3』均為(k×L+r)×(k×L2+r×L)維的矩陣；

其中，

在矩陣H1』中，每行中元素「1」的數量等於L，每列中元素「1」的數量等於1，每行中的L個元素「1」是連續的；

在矩陣H2』中，每行中元素「1」的數量等於L，每列中元素「1」的數量等於1，矩陣H2』由L個矩陣H4』組成，矩陣H4』為(k×L+r)×(k×L+r)維的對角陣，矩陣H4』的主對角線上的元素都是「1」；

矩陣H3』是將矩陣H5』中第k×L2+b×L+c列與第b×L2+(c-1)×L+c列進行位置互換而得到的，b的取值範圍為0至r-1內的所有整數，c的取值範圍為1至L內的所有整數；

矩陣H5』中第1行至k×L行與第1列至k×L2列對應的矩陣等於矩陣H6』，矩陣H5』中第k×L+1行至第k×L+r行與第k×L2+1列至k×L2+r×L列對應的矩陣等於矩陣H7』，矩陣H5』中矩陣H6』和矩陣H7』之外的元素均為「0」；

矩陣H6』為(k×L)×(k×L2)維的矩陣，矩陣H7』為r×(r×L)維的矩陣，矩陣H6』等於矩陣H3，在矩陣H7』中，每行中元素「1」的數量為L，每列中元素「1」的數量等於1，每行的L個元素「1」是連續的。

在第二方面的第一種可能的實現方式中，所述LDPC校驗矩陣為所述矩陣H。

在第二方面的第二種可能的實現方式中，所述LDPC校驗矩陣是對所述矩陣H進行隨機行置換和/或隨機列置換而得到的。

第三方面，本發明實施例提供了一種基於校驗矩陣的裝置，包括：

獲取單元，用於獲取數據；

生成單元，用於通過利用LDPC校驗矩陣對所述第一獲取單元獲取到的所述數據進行編碼，生成編碼數據，所述LDPC校驗矩陣是基於矩陣H生成的，在矩陣H中，每行中元素「1」的數量為L，每列中元素「1」的數量為3，矩陣H為m×n維的矩陣；

m/3＝k×L且k為正整數，矩陣H由矩陣H1、矩陣H2和矩陣H3組成，矩陣H1構成矩陣H的第1行至第m/3行，矩陣H2構成矩陣H的第m/3+1行至第2m/3行，矩陣H3構成矩陣H的第2m/3+1行至第m行，矩陣H1、矩陣H2和矩陣H3均為(k×L)×(k×L2)維的矩陣；

其中，

在矩陣H1中，每行中元素「1」的數量等於L，每列中元素「1」的數量等於1，每行中的L個元素「1」是連續的；

在矩陣H2中，每行中元素「1」的數量等於L，每列中元素「1」的數量等於1，矩陣H2由L個矩陣H4組成，矩陣H4為(k×L)×(k×L)維的對 角陣，矩陣H4的主對角線上的元素都是「1」；

在矩陣H3中，每行中的元素「1」的數量為L，每列中的元素「1」的數量為1，矩陣H3包括k個矩陣H5，矩陣H5包括L個矩陣H6，矩陣H5為L×L2維的矩陣，矩陣H6為L×L維的對角陣，矩陣H6的主對角線上的元素都是「1」；

在矩陣H3中，所述k個矩陣H5之外的元素均為「0」，所述k個矩陣H5中第i個矩陣等於矩陣H3中第(i-1)×L+1行至i×L行與第(i-1)×L2+1列至第i×L2列對應的矩陣，i的取值範圍為1至k中的所有整數；

或者，

m/3＝k×L+r且k為正整數、r為1至L-1範圍內的正整數，矩陣H由矩陣H1』、矩陣H2』和矩陣H3』組成，矩陣H1』構成矩陣H的第1行至第m/3行，矩陣H2』構成矩陣H的第m/3+1行至第2m/3行，矩陣H3』構成矩陣H的第2m/3+1行至第m行，矩陣H1』、矩陣H2』和矩陣H3』均為(k×L+r)×(k×L2+r×L)維的矩陣；

其中，

在矩陣H1』中，每行中元素「1」的數量等於L，每列中元素「1」的數量等於1，每行中的L個元素「1」是連續的；

在矩陣H2』中，每行中元素「1」的數量等於L，每列中元素「1」的數量等於1，矩陣H2』由L個矩陣H4』組成，矩陣H4』為(k×L+r)×(k×L+r) 維的對角陣，矩陣H4』的主對角線上的元素都是「1」；

矩陣H3』是將矩陣H5』中第k×L2+b×L+c列與第b×L2+(c-1)×L+c列進行位置互換而得到的，b的取值範圍為0至r-1內的所有整數，c的取值範圍為1至L內的所有整數；

矩陣H5』中第1行至k×L行與第1列至k×L2列對應的矩陣等於矩陣H6』，矩陣H5』中第k×L+1行至第k×L+r行與第k×L2+1列至k×L2+r×L列對應的矩陣等於矩陣H7』，矩陣H5』中矩陣H6』和矩陣H7』之外的元素均為「0」；

矩陣H6』為(k×L)×(k×L2)維的矩陣，矩陣H7』為r×(r×L)維的矩陣，矩陣H6』等於矩陣H3，在矩陣H7』中，每行中元素「1」的數量為L，每列中元素「1」的數量等於1，每行的L個元素「1」是連續的。

在第三方面的第一種可能的實現方式中，所述LDPC校驗矩陣為所述矩陣H。

在第三方面的第二種可能的實現方式中，所述LDPC校驗矩陣是對所述矩陣H進行隨機行置換和/或列置換而得到的。

第四方面，本發明實施例提供了一種基於校驗矩陣的裝置，包括：

獲取單元，用於獲取編碼數據；

生成單元，用於通過利用LDPC校驗矩陣對所述獲取模塊獲取到的所述編碼數據進行解碼，生成數據，所述LDPC校驗矩陣是基於矩陣H生成的，在矩陣H中，每行中元素「1」的數量為L，每列中元素「1」的數量為3；矩陣H為m×n維的矩陣；

m/3＝k×L且k為正整數，矩陣H由矩陣H1、矩陣H2和矩陣H3組成，矩陣H1構成矩陣H的第1行至第m/3行，矩陣H2構成矩陣H的第m/3+1行至第2m/3行，矩陣H3構成矩陣H的第2m/3+1行至第m行，矩陣H1、矩陣H2和矩陣H3均為(k×L)×(k×L2)維的矩陣；

其中，

在矩陣H1中，每行中元素「1」的數量等於L，每列中元素「1」的數量等於1，每行中的L個元素「1」是連續的；

在矩陣H2中，每行中元素「1」的數量等於L，每列中元素「1」的數量等於1，矩陣H2由L個矩陣H4組成，矩陣H4為(k×L)×(k×L)維的對角陣，矩陣H4的主對角線上的元素都是「1」；

在矩陣H3中，每行中的元素「1」的數量為L，每列中的元素「1」的數量為1，矩陣H3包括k個矩陣H5，矩陣H5包括L個矩陣H6，矩陣H5為L×L2維的矩陣，矩陣H6為L×L維的對角陣，矩陣H6的主對角線上的元素都是「1」；

在矩陣H3中，所述k個矩陣H5之外的元素均為「0」，所述k個矩陣H5中第i個矩陣等於矩陣H3中第(i-1)×L+1行至i×L行與第(i-1)×L2+1列至第i×L2列對應的矩陣，i的取值範圍為1至k中的所有整數；

或者，

m/3＝k×L+r且k為正整數、r為1至L-1範圍內的正整數，矩陣H由矩陣H1』、矩陣H2』和矩陣H3』組成，矩陣H1』構成矩陣H的第1行至第m/3行，矩陣H2』構成矩陣H的第m/3+1行至第2m/3行，矩陣H3』構成矩陣H的第2m/3+1行至第m行，矩陣H1』、矩陣H2』和矩陣H3』均為(k×L+r)×(k×L2+r×L)維的矩陣；

其中，

在矩陣H1』中，每行中元素「1」的數量等於L，每列中元素「1」的數量等於1，每行中的L個元素「1」是連續的；

在矩陣H2』中，每行中元素「1」的數量等於L，每列中元素「1」的數量等於1，矩陣H2』由L個矩陣H4』組成，矩陣H4』為(k×L+r)×(k×L+r)維的對角陣，矩陣H4』的主對角線上的元素都是「1」；

矩陣H3』是將矩陣H5』中第k×L2+b×L+c列與第b×L2+(c-1)×L+c列進行位置互換而得到的，b的取值範圍為0至r-1內的所有整數，c的取值範圍為1至L內的所有整數；

矩陣H5』中第1行至k×L行與第1列至k×L2列對應的矩陣等於矩陣H6』，矩陣H5』中第k×L+1行至第k×L+r行與第k×L2+1列至k×L2+r×L列對應的矩陣等於矩陣H7』，矩陣H5』中矩陣H6』和矩陣H7』之外的元素均為「0」；

矩陣H6』為(k×L)×(k×L2)維的矩陣，矩陣H7』為r×(r×L)維的矩陣，矩陣H6』等於矩陣H3，在矩陣H7』中，每行中元素「1」的數量為L，每列中元素「1」的數量等於1，每行的L個元素「1」是連續的。

在第四方面的第一種可能的實現方式中，所述LDPC校驗矩陣為所述矩陣H。

在第四方面的第二種可能的實現方式中，所述LDPC校驗矩陣是對所述矩陣H進行隨機行置換和/或列置換而得到的。

與現有技術相比，本發明實施例至少具有以下優點：

採用本發明實施例的技術方案，LDPC校驗矩陣是基於m×n維的矩陣H而生成的，矩陣H是由三個(m/3)×n維的子矩陣組成，在這三個子矩陣中，每行中元素「1」的數量為L，每列中元素「1」的數量為1，並且，以A表示矩陣中任意兩個同一行上的元素「1」之間間隔的元素數量，這三個子矩陣對應A的取值範圍是各不相同的，因此，矩陣H中任意兩行與任意兩列的四個交匯的元素處均至少存在一個「0」，可見，矩陣H對應的TG的圍長大於4，這就可以保證LDPC校驗矩陣對應的TG的圍長大於4，因此，採用這樣的LDPC校驗矩陣對數據進行編碼和解碼，當傳輸中的LDPC碼的信噪比比較低時，對接收到的LDPC碼進行解碼得到的數據的的誤比特率較低，因此，LDPC碼的性能得以提高。

附圖說明

為了更清楚地說明本發明實施例或現有技術中的技術方案，下面將對實施例或現有技術描述中所需要使用的附圖作簡單地介紹，顯而易見地，下面描述中的附圖僅僅是本申請中記載的一些實施例，對於本領域普通技術人員來講，還可以根據這些附圖獲得其他的附圖。

圖1為本發明實施例中一種LDPC校驗矩陣H與TG之間對應關係的示意圖；

圖2為本發明實施例中一種對應最小圍長的LDPC校驗H與TG的示意圖；

圖3為本發明實施例提供的一應用場景所涉及的系統框架示意圖；

圖4為本發明實施例中一種基於校驗矩陣的編碼方法的流程示意圖；

圖5為本發明實施例中一種矩陣H示例中元素排布的示意圖；

圖6為本發明實施例中一種矩陣H示例的構造示意圖；

圖7a為本發明實施例中構造一種矩陣H涉及到的矩陣示意圖；

圖7b為本發明實施例中構造一種矩陣H涉及到的矩陣示意圖；

圖8為本發明實施例中一種基於校驗矩陣的解碼方法的流程示意圖；

圖9為本發明實施例中一種基於校驗矩陣的裝置的結構示意圖；

圖10為本發明實施例中一種基於校驗矩陣的裝置的結構示意圖；

圖11為本發明實施例中一種編碼器的結構示意圖；

圖12為本發明實施例中一種解碼器的結構示意圖。

具體實施方式

為了使本技術領域的人員更好地理解本發明中的方案，下面將結合本發明實施例中的附圖，對本發明實施例中的技術方案進行清楚地描述。顯然，所描述的實施例僅是本發明一部分實施例，而不是全部的實施例。

需要說明的是，本申請提及的術語「交匯處」，是指同時位於矩陣中相交的某行和某列的元素的位置。每個交匯處由矩陣中的一個元素佔據。可以理解，矩陣中的一行與一列構成一個交匯處。矩陣中的兩行與兩列構成4個交匯處。此外，本申請中，對於一個矩陣一行來說，該行上任意兩個元素「1」之間的元素個數的取值範圍，稱之為該行的取值範圍。如果一個矩陣的每一行中任意兩個元素「1」之間的元素個數具有相同的取值範圍，則該取值範圍即稱之為該矩陣的取值範圍。例如，對於一個3行的矩陣來說，第1行中任意兩個元素「1」之間至少具有a個元素且至多具有b個元素，第2行中任意兩個元素「1」之間至少具有a個元素且至多具有b個元素，第3行中任意兩個元素「1」之間至少具有a個元素且至多具有b個元素，則第1、2、3行的取值範圍均為[a,b]，則該矩陣的取值範圍為[a,b]。

發明人經過研究發現，在現有技術中，組成LDPC校驗矩陣的多個子矩陣是由同一子矩陣經過隨機列置換而形成的，導致LDPC校驗矩陣對應的TG的圍長等於4。而LDPC碼的性能高低與LDPC校驗矩陣對應的TG的圍長有關，當LDPC校驗矩陣對應的TG的圍長等於4時，LDPC碼的性能較低，也即，當傳輸中的LDPC碼的信噪比比較低時，對接收到的LDPC碼進行解碼得到的數據的誤比特率就會比較高。

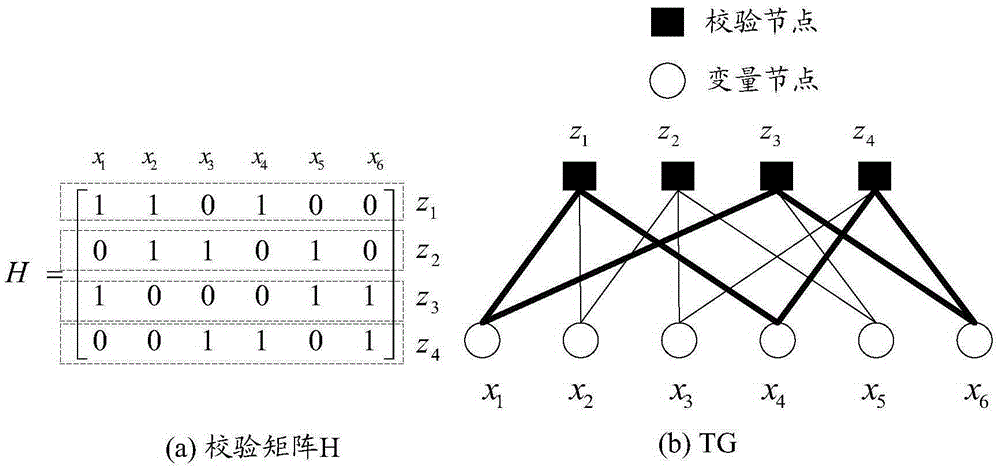
圖1所示的是LDPC校驗矩陣H與TG之間的對應關係。圖1包括(a)校驗矩陣H以及(b)TG。圖1所示的LDPC校驗矩陣H與圖1所示的TG是相 對應的。其中，該TG包括變量節點x1～x6和校驗節點z1～z4。可見，矩陣H的每一列分別對應TG上的一個變量節點，矩陣H的每一行分別對應TG的一個校驗節點。對於任意一個變量節點xi與任意一個校驗節點zj來說，如果矩陣H中xi所在列與zj所在行交匯處的元素為「1」，則TG上xi與zj是相連的(參見圖1中的(b)TG中的粗線)。如果矩陣H中xi所在列與zj所在行交匯處的元素為「0」，則TG上xi與zj是不相連的(參見圖1中的(b)TG中的細線)。

可以理解的是，如果要在TG上形成一個環，那麼這個環至少要包括兩個變量節點和兩個校驗節點，也就是說，TG理論上的最小圍長為4。圖2所示的是對應最小圍長的LDPC校驗矩陣H與TG。圖2包括(a)girth為4的校驗矩陣H和(b)girth 4的校驗矩陣所對應的TG。圖2所示的LDPC校驗矩陣H與圖2所示的TG是相對應的。在該矩陣H上，變量節點x1、x2所在的兩行與校驗節點z1、z2所在的兩列形成了四個交匯處，這四個交匯處的元素均為「1」。因此，在該TG上就形成了由兩個變量節點和兩個校驗節點構成的最短環。因此，該TG的圍長為4。由此可見，如果矩陣H上包含滿足如下第一約束條件的兩行與兩列，則該矩陣H對應的TG圍長即為4。所述第一約束條件為所述兩行與所述兩列的四個交匯處的元素都為「1」。如果矩陣H上每兩行與每兩列均滿足如下第二約束條件，則該矩陣H對應的TG圍長就大於4。所述第二約束條件為每兩行與每兩列的四個交匯處的元素均至少存在一個「0」。

在現有技術中，LDPC校驗矩陣H由多個子矩陣H1～HJ構成。在每個子矩陣的內部，每一列都只有一個元素「1」。因此，對於任一子矩陣內部的任意兩行來說，這兩行與任意兩列的四個交匯處的元素至少存在兩個「0」。但是，矩陣H2～HJ都是由子矩陣H1通過隨機列置換得到的，在這種構造下，對於矩陣H中來自兩個不同子矩陣的兩行來說，無法保證這兩行與矩陣H的任意兩列的四個交匯處的元素必然存在至少一個「0」，因此，現有技術無法保證LDPC校驗矩陣對應的TG的圍長大於4，從而導致了LDPC碼的性能低。

在本發明實施例中，為了提升LDPC碼的性能，提供了一種基於校驗矩陣的編解碼方法和裝置。其中，在用於編解碼的LDPC校驗矩陣中，任意兩行與任意兩列的四個交匯處的元素均至少存在一個「0」，從而保證LDPC校驗矩陣對應的TG的圍長大於4。

圖3為本發明實施例提供的技術方案的一種應用場景所涉及的系統框架示意圖。參見圖3，本發明實施例提供的技術方案可以應用到由編碼器301與解碼器302組成的系統中。在該系統中，編碼器301與解碼器302可以採用相同的LDPC校驗矩陣實現數據編碼和數據解碼。具體地，編碼器301對於獲取到的數據，可以通過利用LDPC校驗矩陣對該數據進行編碼，生成編碼數據。解碼器302在獲取到該編碼數據時，可以通過利用所述LDPC校驗矩陣對該數據進行編碼，生成該數據。

需要注意的是，上述應用場景僅是為了便於理解本發明的原理而示出，不用於限定本發明實施例提供的技術方案。

下面結合附圖，通過實施例來詳細說明本發明中基於校驗矩陣的編解碼和設備的實現方式。

圖4為本發明實施例中一種基於校驗矩陣的編碼方法的流程示意圖。在本實施例中，所述方法可以包括如下步驟：

步驟401、編碼器獲取數據。

步驟402、所述編碼器通過利用LDPC校驗矩陣對所述數據進行編碼，生成編碼數據。

具體實現時，所述數據可以是比特串。所述編碼數據可以是編碼比特串。編碼器在獲取到所述比特串時，可以利用LDPC校驗矩陣對該比特串進行編碼，從而生成編碼比特串。該編碼比特串可以用於在數據鏈路中傳輸。例如，所述數據鏈路可以是光纜、電纜等物理鏈路，也可以是標籤交換路徑(Label Switching Path，簡稱LSP)、偽線(Pseudo Wire，簡稱PW)等邏輯鏈路。

在本實施例中，用於編碼的LDPC校驗矩陣是基於矩陣H生成的。矩陣H是一個m×n維的矩陣。在矩陣H中，每行中元素「1」的數量為L，每列中元素「1」的數量為3。可見，矩陣H中元素「1」的總數量可以表示為m×L，也可以表示為3×n，因此，m×L＝3×n，也即，n＝m/3×L。其中，m、n可以由LDPC校驗矩陣的實際應用場景來確定。其中，n的取值取決於實際鏈路中的數據幀長，m的取值取決於編碼數據的淨荷長度例如，若實際鏈路的數據幀長為5000並且數據幀長中要求至少要傳輸3000bit的有用數據，n的取值為 5000，m的取值為5000-3000，即2000。

為了便於構造對應TG的圍長大於4的矩陣H，可以將矩陣H劃分成三個子矩陣，這三個子矩陣分別構成矩陣H的第1行至第m/3行、第m/3+1行至第2m/3行、第2m/3+1行至第m行。在每個子矩陣中，每行中元素「1」的數量為L，每列中元素「1」的數量為1。在這種情況下，在每個子矩陣內部，任意兩行與任意兩列的四個交匯處的元素均至少存在兩個「0」，因此，在構造每個子矩陣時，僅需要考慮矩陣H中來自兩個不同子矩陣的兩行與矩陣中任意兩列的四個交匯處的元素是否必然存在「0」。

在矩陣H的每一個子矩陣中，各行的取值範圍可以是相同的，因此，對於任意一個子矩陣來說，該子矩陣上各行的取值範圍即是該子矩陣的取值範圍，而任意兩個子矩陣的取值範圍可以是沒有交集的，此時，矩陣H中位於兩個不同子矩陣的任意兩行與矩陣H中任意兩列的四個交匯的元素處必然存在「0」。舉例來說，圖5為一種矩陣H示例的結構示意圖。該矩陣H的行數不小於2，列數不小於13。圖5示出了矩陣H的第i行和第j行，以及第z-6列至第z+6列。具體地說，假設兩個不同的子矩陣分別對應取值範圍[0,2]和[3,4]，分別來自這兩個子矩陣的i行、j行與z列的兩個交匯處的元素均為「1」，在i行上的其餘元素「1」僅可能出現在第z-3列至第z-1列或第z+1列至第z+3列，在j行上的其餘元素「1」僅可能出現在第z-4列至第z-5列或第z+4列至第z+5列，也即，i行、j行僅與z列的兩個交匯處的元素都為「1」，與其他列的兩個交匯處的元素都至少存在一個「0」。可見，當各個子矩陣的取值範圍各不相同時，對於矩陣H的任意兩行來說，如果這兩行分別位於兩個不同的子矩陣，則這兩行與矩陣H的任意兩列的四個交匯處的元素中就必然存在「0」。

需要說明的是，為了使得任意兩個子矩陣對應的取值範圍沒有交集，可以根據m/3是否能被L整除，採用不同的方式來構造矩陣H的各子矩陣。當m/3能夠被L整除時，採用下述第一種情況介紹的矩陣H，當m/3不能夠被L整除時，採用下述第二種情況介紹的矩陣H，也即，本實施例可以採用下述第一情況的矩陣H，或者，也可以採用下述第二種情況的矩陣H。

第一種情況：m/3＝k×L且k為正整數，即m/3能夠被L整除。

在第一種情況下，矩陣H可以表示為：

具體地，矩陣H可以由矩陣H1、矩陣H2和矩陣H3組成，也即，矩陣H1、矩陣H2和矩陣H3是矩陣H的三個子矩陣。矩陣H1可以構成矩陣H的第1行至第m/3行，矩陣H2可以構成矩陣H的第m/3+1行至第2m/3行，矩陣H3可以構成矩陣H的第2m/3+1行至第m行。可見，矩陣H1、矩陣H2和矩陣H3均為(m/3)×n維。考慮到第一種情況下m/3＝k×L，因此，矩陣H1、矩陣H2和矩陣H3的維數也均可以表示成(k×L)×(k×L2)維。

對於(k×L)×(k×L2)維的矩陣H1，矩陣H1的總列數是能夠被L整除的，因此，矩陣H1可以按照如下方式來構造：

在矩陣H1中，每行中元素「1」的數量等於L，每列中元素「1」的數量等於1，每行中的L個元素「1」是連續的。例如，在矩陣H1第1行中，位於第1至L列的元素為「1」，其餘元素為「0」。又如，在矩陣H1第2行中，位於第1至L列的元素為「1」，其餘元素為「0」。

可見，在矩陣H1的第a1行中，元素「1」均位於第(a1-1)×L+b1列，其中，a1的取值範圍為1至k×L中的所有整數，b1的取值範圍為1至L中的所有整數。

對於矩陣H1中的任意一行來說，由於該行上所有的L個元素是連續排列在一起的，因此，該行的取值範圍的最小值為0，該行的取值範圍最大值為L-2。可見，以A1表示矩陣H1中任意一行上任意兩個元素「1」之間的元素個數，矩陣H1的取值範圍為A1≤L-2。

對於(k×L)×(k×L2)維的矩陣H2，矩陣H2的總列數是能夠被總行數整除的，並且，整除的商是L。因此，矩陣H2可以按照如下方式來構造：

在矩陣H2中，每行中元素「1」的數量等於L，每列中元素「1」的數量等於1，矩陣H2由L個矩陣H4組成，矩陣H4為(k×L)×(k×L)維的對角陣，矩陣H4的主對角線上的元素都是「1」。

具體地，在矩陣H2中，第1至k×L列構成一個矩陣H4，第k×L+1列至第k×L×2列構成另一個H4，第k×L×2+1列至第k×L×3列構成又一個H4，……，第k×L×(L-1)+1列至第k×L2列構成又一個H4。在任意一個矩陣H4中，位於第1行第1列的元素為「1」，位於第2行第2列的元素為「1」，……，位於第k×L行第k×L列的元素為「1」，其餘元素均為「0」。

可見，在矩陣H2的第a2行中，元素「1」均位於第a2+b2×k×L列，其中，a2的取值範圍為1至k×L中的所有整數，b2的取值範圍為0至L-1中的所有整數。例如，在矩陣H2第1行中，位於第1、k×L+1、k×L×2+1、……、k×L×(L-1)+1列的元素為「1」。又如，在矩陣H2第2行中，位於第2、k×L+2、k×L×2+2、……、k×L×(L-1)+2列的元素為「1」。

對於矩陣H2中的任意一行來說，該行上每兩個相距最近的元素「1」之間均具有有k×L-1個元素「0」，並且，該行上元素「1」的數量為L，可見，該行的取值範圍的最小值為k×L-1，該行的取值範圍的最大值為k×L×(L-1)-1。可見，以A2表示矩陣H2中任意一行上任意兩個元素「1」之間的元素個數，矩陣H2的取值範圍為k×L-1≤A2≤k×L×(L-1)-1。

對於(k×L)×(k×L2)維的矩陣H3，矩陣H3的總列數能夠被L2整除且整除得到的商為k，矩陣H3的總行數能夠被L整除且整除得到的商也為k。因此，矩陣H3可以按照如下方式來構造：

在矩陣H3中，每行中元素「1」的數量等於L，每列中元素「1」的數量 等於1，矩陣H3包括k個矩陣H5，矩陣H5包括L個矩陣H6，矩陣H5為L×L2維的矩陣，矩陣H6為L×L維的對角陣，矩陣H6的主對角線上的元素都是「1」。在矩陣H3中，所述k個矩陣H5之外的元素均為「0」，所述k個矩陣H5中第i個矩陣等於矩陣H3中第(i-1)×L+1行至i×L行與第(i-1)×L2+1列至第i×L2列對應的矩陣，i的取值範圍為1至k中的所有整數。

具體地，在矩陣H3中，第1行至第L行與第1列至第L2列構成第1個矩陣H5，即對應於i取1，第L+1行至第2×L行至第L2+1列至第2×L2列構成第2個矩陣H5，即對應於i取2，……，第(k-1)×L+1行至k×L行與第(k-1)×L2+1列至第k×L2列構成第i個矩陣H5，即對應於i取k。在任意一個矩陣H5中，第1列至第L列構成一個矩陣H6，第L+1列至第2×L列構成另一個矩陣H6，……，第(L-1)×L列至第L2列構成又一個矩陣H6。在任意一個矩陣H6中，位於第1行第1列的元素為「1」，位於第2行第2列的元素為「1」，……，位於第L行第L列的元素為「1」，其餘元素均為0。

可見，在矩陣H3的第a3+b3×L行中，元素「1」均位於第a3+b3×L2+c3×L列，其中，a3的取值範圍為1至L中的所有整數，b3的取值範圍為0至k-1中的所有整數，c3的取值範圍為0至L-1範圍內的所有整數。例如，矩陣H3第1行對應a3取1且b3取0，在矩陣H3第1行中，位於第1、L+1、……、L×(L-1)+1列的元素為「1」。又如，矩陣H3第2行對應a3取2且b3取0，在矩陣H3第2行中，位於第2、L+2、……、L×(L-1)+2列的元素為「1」。再如，矩陣H3第L+1行對應a3取1且b3取1，在矩陣H3第L+1行中，位於第L2+1、L2+L+1、……、L2+L×(L-1)+1列的元素為「1」。

對於矩陣H3中的任意一行來說，該行上每兩個相距最近的元素「1」之間均間隔有L-1個元素「0」，並且，該行上元素「1」的數量為L，可見，該行的取值範圍的最小值為L-1，該行的取值範圍的最大值為L×(L-1)-1。可見，以A3表示矩陣H3中任意一行上任意兩個元素「1」之間的元素個數，矩陣H3的取值範圍為L-1≤A3≤L×(L-1)-1。

作為一種示例，根據前述矩陣H1、矩陣H2和矩陣H3的構造方式，當k＝3且L＝2時，矩陣H可以構造成如圖6所示的形式。

需要說明的是，對於本實施例第一種情況的矩陣H，在k大於L的情況 下，上述A1、A2、A3的取值範圍是互不相同的，因此，該矩陣H中任意兩行與任意兩列的四個交匯處的元素均至少存在一個「0」，因此，該矩陣H對應TG的圍長不為4。

具體地，以i行和j行表示矩陣H的任意兩行。i行與j行可以位於矩陣H的同一子矩陣，即，i行與j行可以均位於矩陣H1、矩陣H2和矩陣H3中的任意一個矩陣。i行與j行也可以位於矩陣H的兩個不同的子矩陣，即，i行與j行可以分別位於矩陣H1、矩陣H2和矩陣H3中的任意兩個矩陣。

在i行與j行位於同一子矩陣的情況下，由於矩陣H1、矩陣H2和矩陣H3的每列中均有且只有一個元素「1」，因此，i行、j行與矩陣H中任意一列的兩個交匯處的元素都至少存在一個「0」。

在i行與j行位於不同子矩陣的情況下，i行可以位於矩陣H1，j行可以位於矩陣H2。假設矩陣H中存在一個z列使得i行、j行與z列的兩個交匯處的元素均為「1」，根據矩陣H1的取值範圍和矩陣H2的取值範圍，除了z列上的元素「1」之外，i行上的其他元素「1」僅可能位於第z-L+1列至第z+L-1列，j行上的其他元素「1」僅可能位於第z-k×L×(L-1)列至第z-k×L列及第z+k×L列至第z+k×L×(L-1)列，可見，在k為正整數的情況下，除了z列之外，i行的元素「1」與j行的元素「1」不會同時出現在同一列上，因此，i行、j行與任意兩列的四個交匯處的元素中都至少存在一個「0」。

在i行與j行位於不同子矩陣的情況下，i行可以位於矩陣H1，j行可以位於矩陣H3。假設矩陣H中存在一個z列使得i行、j行與z列的兩個交匯處的元素均為「1」，根據矩陣H1的取值範圍和矩陣H3的取值範圍，除了z列上的元素「1」之外，i行上的其他元素「1」僅可能位於第z-L+1列至第z+L-1列，j行上的其他元素「1」僅可能位於第z-L×(L-1)列至第z-L列及第z+L列至第z+L×(L-1)列，可見，除了z列之外，i行的元素「1」與j行的元素「1」不會同時出現在同一列上，因此，i行、j行與任意兩列的四個交匯處的元素中都至少存在一個「0」。

在i行與j行位於不同子矩陣的情況下，i行可以位於矩陣H2，j行可以位於矩陣H3。假設矩陣H中存在一個z列使得i行、j行與z列的兩個交匯處的元素均為「1」，根據矩陣H2的取值範圍和矩陣H3的取值範圍，除了z列上的 元素「1」之外，i行上的其他元素「1」僅可能位於第z-k×L×(L-1)列至第z-k×L列及第z+k×L列至第z+k×L×(L-1)列，j行上的其他元素「1」僅可能位於第z-L×(L-1)列至第z-L列及第z+L列至第z+L×(L-1)列，可見，在k大於L的情況下，除了z列之外，i行的元素「1」與j行的元素「1」不會同時出現在同一列上，因此，i行、j行與任意兩列的四個交匯處的元素中都至少存在一個「0」。

通過上述分析可知，對於矩陣H中的任意兩行，無論這兩行是均位於矩陣H1、矩陣H2和矩陣H3中的任意一個矩陣，還是分別位於矩陣H1、矩陣H2和矩陣H3中的任意兩個矩陣，這兩行與矩陣H中任意兩列的四個交匯處的元素都至少存在一個「0」，因此，矩陣H對應的TG的圍長大於4。

第二種情況：m/3＝k×L+r且k為正整數、r為1至L-1範圍內的正整數，即m/3不能夠被L整除。

在第二種情況下，矩陣H可以表示為：

具體地，矩陣H可以由矩陣H1』、矩陣H2』和矩陣H3』組成，也即，矩陣H1』、矩陣H2』和矩陣H3』是矩陣H的三個子矩陣。矩陣H1』可以構成矩陣H的第1行至第m/3行，矩陣H2』可以構成矩陣H的第m/3+1行至第2m/3行，矩陣H3』可以構成矩陣H的第2m/3+1行至第m行。可見，矩陣H1』、矩陣H2』和矩陣H3』均為(m/3)×n維。考慮到第一種情況下m/3＝k×L+r，因此，矩陣H1』、矩陣H2』和矩陣H3』的維數也可以表示成(k×L+r)×(k×L2+r×L)維的矩陣。

對於(k×L+r)×(k×L2+r×L)維的矩陣H1』，矩陣H1』的總列數是能夠被L整除的。因此，矩陣H1』可以按照如下方式來構造：

其中，

在矩陣H1』中，每行中元素「1」的數量等於L，每列中元素「1」的數量 等於1，每行中的L個元素「1」是連續的。例如，在矩陣H1』第1行中，位於第1至L列的元素為「1」，其餘元素為「0」。又如，在矩陣H1』第2行中，位於第1至L列的元素為「1」，其餘元素為「0」。

可見，在矩陣H1』的第a1』行中，元素「1」均位於第(a1』-1)×L+b1』列，其中，a1』的取值範圍為1至k×L+r中的所有整數，b1』的取值範圍為1至L中的所有整數。

可以理解的是，由於矩陣H1』與前述矩陣H1在每行上對元素「1」採用了相似的排列方式，參考前述矩陣H1可知，以A1』表示矩陣H1』中任意一行上任意兩個元素「1」之間的元素個數，矩陣H1』的取值範圍為A1』≤L-2。

對於(k×L+r)×(k×L2+r×L)維的矩陣H2』，矩陣H2』的總列數是能夠被總行數整除的，並且，整除得的商是L。因此，矩陣H2可以按照如下方式來構造：

在矩陣H2』中，每行中元素「1」的數量等於L，每列中元素「1」的數量等於1，矩陣H2由L個矩陣H4』組成，矩陣H4』為(k×L+r)×(k×L+r)維的對角陣，矩陣H4』的主對角線上的元素都是「1」。

具體地，在矩陣H2』中，第1至k×L+r列構成一個矩陣H4』，第k×L+r+1列至第k×L×2+r×2列構成另一個H4』，……，第k×L×(L-1)+r×(L-1)+1列至第k×L2+r×L列構成又一個H4』。在任意一個矩陣H4』中，元素「1」位於第1行第1列、第2行第2列、……、第k×L+r行第k×L+r列的位置。

可見，在矩陣H2』的第a2』行中，元素「1」均位於第a2』+b2』×(k×L+r)列，其中，a2的取值範圍為1至k×L+r中的所有整數，b2』的取值範圍為0至L-1中的所有整數。例如，在矩陣H2』第1行中，元素「1」位於第1、k×L+r+1、k×L×2+r×2+1、……、k×L×(L-1)+r×(L-1)+1列。又如，在矩陣H2』第2行中，元素「1」位於第2、k×L+r+2、k×L×2+r×2+2、……、k×L×(L-1)+r×(L-1)+2列。

可以理解的是，由於矩陣H2』與前述矩陣H2在每行上對元素「1」採用了相似的排列方式，參考前述矩陣H2可知，以A2』表示矩陣H2』中任意一行上任 意兩個元素「1」之間的元素個數，矩陣H2』的取值範圍為k×L+r-1≤A2』≤(k×L+r)×(L-1)-1。

對於(k×L+r)×(k×L2+r×L)維的矩陣H3』，矩陣H3』的總列數不能夠被L2整除，矩陣H3』的總列數除以L2，商為k，餘數為r×L，並且，矩陣H3的總行數不能夠被L整除，矩陣H3』的總行數除以L，商為k，餘數為r。因此，可以先構造一個(k×L+r)×(k×L2+r×L)維的矩陣H5』，再對矩陣H5』進行列置換可以得到矩陣H3』。其中，矩陣H5』可以按照如下方式來構造：

在矩陣H5』中，第1行至k×L行與第1列至k×L2列對應的矩陣等於矩陣H6』，第k×L+1行至第k×L+r行與第k×L2+1列至k×L2+r×L列對應的矩陣等於矩陣H7』，矩陣H5』中矩陣H6』和矩陣H7』之外的元素均為「0」。矩陣H6』為(k×L)×(k×L2)維的矩陣，矩陣H6』等於矩陣H3。矩陣H7』為r×(r×L)維的矩陣，在矩陣H7』中，每行中元素「1」的數量為L，每列中元素「1」的數量等於1，每行的L個元素「1」是連續的。

具體地，矩陣H6』與前述矩陣H3均是(k×L)×(k×L2)維的矩陣，因此可以採用矩陣H3作為矩陣H6』。參照矩陣H3可知，在矩陣H6』中的第a6』+b6』×L行中，元素「1」均位於第a6』+b6』×L2+c6』×L列，其中，a6』的取值範圍為1至L中的所有整數，b6』的取值範圍為0至k-1中的所有整數，c6』的取值範圍為0至L-1範圍內的所有整數。

矩陣H7』與前述矩陣H1具有相似的特點，兩者均是總列數除以總行數的商為L，因此參照矩陣H1，可以將矩陣H7』每行上的元素「1」連續排列在一起，即，在矩陣H7』中的第a7』行，元素「1」均位於第(a7』-1)×L+b7』列，其中，a7』的取值範圍為1至r中的所有整數，b7』的取值範圍為1至L中的所有整數。

由矩陣H6』和矩陣H7』可知，在矩陣H5』第1行至第k×L行中的第a5』+b5』×L行中，元素「1」均位於第a5』+b5』×L2+c5』×L列，在矩陣H5』第k×L+1行至第k×L+r行中的第d5』+k×L行中，元素「1」均位於第(d5』-1)×L+e5』+k×L2列，其中，a5』- 的取值範圍為1至L中的所有整數，b5』的取值範圍為0至k-1中的所有整數，c5』的取值範圍為0至L-1範圍內的所有整數，d5』的取值範圍為1至r中的所有整數，e5』的取值範圍為1至L中的所有整數。例如，矩陣H5』第1行對應a5』取1且b5』取0，在矩陣H5』第1行中，元素「1」位於第1、L+1、……、L×(L-1)+1列。又如，矩陣H5』第k×L行對應a5』取L且b5』取k-1，在矩陣H5』第k×L行中，元素「1」位於第L、L×2、……、L×L列。又如，矩陣H5』第k×L+1行對應d5』取1，在矩陣H5』第k×L+1行中，元素「1」位於第k×L2+1至k×L2+L列的元素。又如，矩陣H5』第k×L+r行對應d5』取r，在矩陣H5』第k×L+r行中，元素「1」位於第k×L2+(r-1)×L+1至k×L2+r×L列。

在矩陣H5』構造完成之後，將矩陣H5』中第k×L2+b×L+c列與第b×L2+(c-1)×L+c列進行位置互換，可以得到矩陣H3』，其中，b的取值範圍為0至r-1內的所有整數，c的取值範圍為1至L內的所有整數。例如，對應b取0且c取1，需要將矩陣H5』中第k×L2+1列與第1列進行位置互換。又如，對應b取1且c取2，需要將矩陣H5』中第k×L2+L+2列與第L2+L+2列進行位置互換。又如，對應b取r-1且c取L，需要將矩陣H5』中第k×L2+r×L列與第r×L2列進行位置互換。

可以理解的是，按照上述方式構造的矩陣H3』，可以表示為：

具體地，矩陣H3』包括矩陣H8』、矩陣H9』、矩陣H10』和矩陣H11』。矩陣H3』中第1行至第r×L行與第1列至第r×L2列對應的矩陣等於矩陣H8』，矩陣H3』中第r×L+1行至第k×L行與第r×L2+1列至第k×L2列對應的矩陣等於矩陣H9』，矩陣H3』中第1行至第r×L行與第k×L2+1列至第k×L2+r×L列對應的矩陣等於矩陣H10』，矩陣H3』中其餘元素為「0」。

矩陣H8』包括r個矩陣H12』，所述r個矩陣H12』中第i個矩陣等於矩陣H8』中第(i-1)×L+1行至第i×L行與第(i-1)×L2+1列至第i×L2列對應的矩陣，i的取值範圍為1至r中的所有整數。所述矩陣H12』是由矩陣H121』、矩陣H122』、……、矩陣H12L』共L個矩陣組成。在矩陣H121』至矩陣H12L』中的任意一個矩陣中，位於主對角線上的L個元素包括L-1個元素「1」和1個元素「0」。在矩陣H121』至矩陣H12L』中的矩陣H12i』中，第i行第i列上的元素為「0」。

矩陣H9』包括k-r個矩陣H13』，所述k-r個矩陣H13』中第i個矩陣等於矩陣H9』中第(i-1)×L+1行至第i×L行與第(i-1)×L2+1列至第i×L2列對應的矩陣，i的取值範圍為1至k-r中的所有整數。矩陣H13』等於前述的矩陣H5。

矩陣H10』為(r×L)×(r×L)維的矩陣，矩陣H10』主對角線上的元素為「1」。

矩陣H11』包括r個矩陣H14』，所述r個矩陣H14』中第i個矩陣等於矩陣H11』中第i行與第(i-1)×L2+1列至第i×L2列對應的矩陣，i的取值範圍為1至r中的所有整數。矩陣H14』包括L個元素「1」。在矩陣H14』中，每兩個相距最近的元素「1」之間間隔有L-1個元素「0」。

由上述構造的矩陣H3』可知，在矩陣H3』第1行至第r×L行中的第a3』+b3』×L行中，元素「1」均位於第a3』+d3』×L2+c3』×L列及第a3+b3』×L+k×L2列，在矩陣H3』第r×L+1行至第k×L行中的第a3』+b3』×L行中，元素「1」均位於第a3』+b3』×L2+c3』×L列，在矩陣H5』第k×L+1行至第k×L+r行中的第e3』+k×L行中，元素「1」均位於第(e3』-1)×L 2+(f5』-1)×L+f5』列，其中，a3』的取值範圍為1至L中的所有整數，b3』的取值範圍為0至k-1中的所有整數，c3』的取值範圍為0至L-1範圍內的所有整數，d3』＝b3』且d3』≠a3』-1，e3』的取值範圍為1至r中的所有整數，f3』的取值範圍為1至L中的所有整數。

在矩陣H3』第1行至第r×L行中的任意一行上，前k×L2列共有L-1個「1」元素，其中，兩個元素「1」之間至少具有L-1個元素，兩個元素「1」之間至多具有L×(L-1)-1個元素。在該行上，位於後r×L列的元素中僅有1個「1」，該元素「1」與位於前k×L2列的元素「1」之間至少具有k×L2-r×L2+r×L-1。在矩陣H3』第r×L+1行至第k×L行中的任意一行上，兩個元素「1」之間至少具有L-1個元素，兩個元素「1」之間至多具有L×(L-1)-1個元素。在矩陣H3』第k×L+1行至第k×L+r行中的任意一行上，兩個元素「1」之間至少具有L個元素，兩個元素「1」之間至多具有L2個元素。由此可見，以A3』表示矩陣H3』中任意一行上任意兩個元素「1」之間的元素個數，矩陣H3』的取值範圍為L-1≤A3』≤L2-1或A3』≥k×L2-r×L2+r×L-1。

作為一種示例，根據前述矩陣H1』、矩陣H2』和矩陣H3』的構造方式，當k＝3、L＝2且r＝1時，矩陣H可以構造成如圖7a和圖7b所示的形式。其中，圖7a示出的是構造矩陣H1』的方式、構造矩陣H2』的方式以及構造矩陣H5』的方式，圖7b示出的是矩陣H5』經過列置換構造矩陣H3』的方式以及矩陣H1』、矩陣H2』和矩陣H3』構造矩陣H的方式。

需要說明的是，對於本實施例第二種情況的矩陣H，在k大於L2-L的情況下，上述矩陣H1』、矩陣H2』、矩陣H3』的取值範圍是互不相同的，因此，該矩陣H中任意兩行與任意兩列的四個交匯處的元素均至少存在一個「0」，因此，該矩陣H對應TG的圍長大於4。

具體地，以i行和j行表示矩陣H的任意兩行。i行與j行可以位於矩陣H的同一子矩陣，即，i行與j行可以均位於矩陣H1』、矩陣H2』和矩陣H3』中 的任意一個矩陣。i行與j行也可以位於矩陣H的兩個不同的子矩陣，即，i行與j行可以分別位於矩陣H1』、矩陣H2』和矩陣H3』中的任意兩個矩陣。

在i行與j行位於同一子矩陣的情況下，由於矩陣H1』、矩陣H2』和矩陣H3』的每列中均有且只有一個元素「1」，因此，i行、j行與矩陣H中任意一列的兩個交匯處的元素都至少存在一個「0」。

在i行與j行位於不同子矩陣的情況下，i行可以位於矩陣H1』，j行可以位於矩陣H2』。假設矩陣H中存在一個z列使得i行、j行與z列的兩個交匯處的元素均為「1」，根據矩陣H1』的取值範圍和矩陣H2』的取值範圍，除了z列上的元素「1」之外，i行上的其他元素「1」僅可能位於第z-L+1列至第z+L-1列，j行上的其他元素「1」僅可能位於第z-(k×L+r)×(L-1)列至第z-k×L-r列及第z+k×L+r列至第z+(k×L+r)×(L-1)列，可見，在k大於L2-L的情況下，除了z列之外，i行的元素「1」與j行的元素「1」不會同時出現在同一列上，因此，i行、j行與任意兩列的四個交匯處的元素中都至少存在一個「0」。

在i行與j行位於不同子矩陣的情況下，i行可以位於矩陣H1』，j行可以位於矩陣H3』。假設矩陣H中存在一個z列使得i行、j行與z列的兩個交匯處的元素均為「1」，根據矩陣H1』的取值範圍和矩陣H3』的取值範圍，除了z列上的元素「1」之外，i行上的其他元素「1」僅可能位於第z-L+1列至第z+L-1列，j行上的其他元素「1」僅可能位於第z-L2列至第z-L列及第z+L列至第z+L2列、第z-k×L2+r×L2-r×L列和第z+k×L2-r×L2+r×L列，可見，除了z列之外，i行的元素「1」與j行的元素「1」不會同時出現在同一列上，因此，i行、j行與任意兩列的四個交匯處的元素中都至少存在一個「0」。

在i行與j行位於不同子矩陣的情況下，i行可以位於矩陣H2』，j行可以位於矩陣H3』。假設矩陣H中存在一個z列使得i行、j行與z列的兩個交匯處元素均為「1」，根據矩陣H2』的取值範圍和矩陣H3』的取值範圍，除了z列上的元素「1」之外，i行上的其他元素「1」僅可能位於第z-(k×L+r)×(L-1)列至第z-k×L-r列及第z+k×L+r列至第z+(k×L+r)×(L-1)列，j行上的其他元素「1」僅可能位於第z-L2列至第z-L列及第z+L列至第z+L2列、第z-k×L2+r×L2-r×L列和第z+k×L2-r×L2+r×L列，可見，在k大於L2-L的情況下，除了z列之外，i行的元素「1」與j行的元素「1」不會同時出現在同一列上，因此，i行、j 行與任意兩列的四個交匯處的元素中都至少存在一個「0」。

通過上述分析可知，對於矩陣H中的任意兩行，無論這兩行是均位於矩陣H1』、矩陣H2』和矩陣H3』中的任意一個矩陣，還是分別位於矩陣H1』、矩陣H2』和矩陣H3』中的任意兩個矩陣，這兩行與矩陣H中任意兩列的四個交匯處的元素都至少存在一個「0」，因此，矩陣H對應的TG圍長大於4。

在一些實施方式中，LDPC校驗矩陣可以是矩陣H。矩陣H本身對應的TG的圍長大於4，即相當於LDPC校驗矩陣對應的TG的圍長大於4。

在另一些實施方式中，LDPC校驗矩陣可以是對矩陣H進行行置換而得到的，即，從矩陣H中選擇任意多行進行位置互換，互換後得到LDPC矩陣。例如，選取矩陣H的第1、5、10行，將第1行換到第5行，將第5行換到第10行，將第10行換到第1行，從而得到LDPC校驗矩陣。

在又一些實施方式中，LDPC校驗矩陣可以是對矩陣H進行列置換而得到的，即，從矩陣H中選擇任意多列進行位置互換，互換後得到LDPC校驗矩陣。例如，選取矩陣H的第3、6、7列，將第3列換到第7列，將第6行換到第3列，將第7列換到第6列，從而得到LDPC校驗矩陣。

在又一些實施方式中，LDPC校驗矩陣可以是對矩陣H進行行置換和列置換而得到的，即，從矩陣H中先選擇任意多行進行位置互換再選擇任意多列進行位置互換，互換後得到LDPC校驗矩陣，或者，從矩陣H中先選擇任意多列進行位置互換再選擇任意多行進行位置互換，互換後得到LDPC校驗矩陣。

可以理解的是，無論是矩陣的行置換還是矩陣的列置換，都不會改變矩陣對應的TG的圍長。因此，通過矩陣H的行置換和/或列置換得到的LDPC校驗矩陣，與矩陣H具有相同的TG的圍長，因此，LDPC校驗矩陣對應的TG的圍長大於4。

需要說明的是，矩陣X中第Y行表示矩陣X從最頂端開始向下的第Y個行向量，矩陣X中第Z列表示矩陣X從最左側開始向右的第Z個行向量，其中，矩陣X可以是上述提及的任意一個矩陣，第Y行可以是上述提及的任意一個矩陣的任意一行，第Z列可以是上述提及的任意一個矩陣的任意一列。

通過本實施例的技術方案，無論是上述第一種情況還是上述第二種情況， m×n維的矩陣H都是由三個(m/3)×n維的子矩陣組成，在這三個子矩陣中，每行中元素「1」的數量為L，每列中元素「1」的數量為1，並且，這三個子矩陣的取值範圍是各不相同的，這使得矩陣H中任意兩行與任意兩列的四個交匯處的元素均至少存在一個「0」，保證矩陣H對應的TG的圍長大於4，因此，基於矩陣H生成LDPC校驗矩陣，就可以保證LDPC校驗矩陣對應的TG的圍長大於4，因此，採用這樣的LDPC校驗矩陣對數據進行編碼，當傳輸中的LDPC碼的信噪比比較低時，對接收到的LDPC碼進行解碼得到的數據的的誤比特率較低，因此，LDPC碼的性能得以提高。

圖8為本發明實施例中一種基於校驗矩陣的解碼方法的流程示意圖。在本實施中，所述方法包括如下步驟：

步驟801、解碼器獲取編碼數據。

步驟802、所述解碼器通過利用低密度奇偶校驗LDPC校驗矩陣對所述編碼數據進行解碼，生成數據。

需要說明的是，圖4所示的方法以及圖8所示的方法可以應用於圖3所示的應用場景。具體地，圖4所示的方法的執行主體可以是圖3中的編碼器301。圖8所示的方法的執行主體可以是圖3中的解碼器302。圖8中步驟801涉及的編碼數據可以是圖4中步驟402涉及的編碼數據。圖8所示的步驟802中的解碼處理是圖4所示的步驟402中的編碼處理的逆處理。因此，圖8所示的步驟802具體實現時，可以參考實施例對圖8所示的步驟802的描述。

具體實現時，解碼器可以以比特串的形式對數據進行獲取和解碼。解碼器在獲取到編碼比特串時，可以利用LDPC校驗矩陣對該編碼比特串進行解碼，從而生成比特串。該編碼比特串可以用於在實際數據鏈路中傳輸。在本實施例中，用於解碼的LDPC校驗矩陣是基於矩陣H生成的。在矩陣H中，每行中元素「1」的數量為L，每列中元素「1」的數量為3，矩陣H為m×n維的矩陣。其中，本實施例可以採用下述第一種情況的矩陣H，或者，也可以採用下述第二種情況的矩陣H。

第一種情況：m/3＝k×L且k為正整數，即m/3能夠被L整除。

在第一種情況下，矩陣H可以表示為：

具體地，矩陣H由矩陣H1、矩陣H2和矩陣H3組成，矩陣H1構成矩陣H的第1行至第m/3行，矩陣H2構成矩陣H的第m/3+1行至第2m/3行，矩陣H3構成矩陣H的第2m/3+1行至第m行，矩陣H1、矩陣H2和矩陣H3均為(k×L)×(k×L2)維的矩陣。

矩陣H1可以按照如下方式來構造：

在矩陣H1中，每行中元素「1」的數量等於L，每列中元素「1」的數量等於1，每行中的L個元素「1」是連續的。

矩陣H2可以按照如下方式來構造：

在矩陣H2中，每行中元素「1」的數量等於L，每列中元素「1」的數量等於1，矩陣H2由L個矩陣H4組成，矩陣H4為(k×L)×(k×L)維的對角陣，矩陣H4的主對角線上的元素都是「1」。

矩陣H3可以按照如下方式來構造：

在矩陣H3中，每行中的元素「1」的數量為L，每列中的元素「1」的數量為1，矩陣H3包括k個矩陣H5，矩陣H5包括L個矩陣H6，矩陣H5為L×L2維的矩陣，矩陣H6為L×L維的對角陣，矩陣H6的主對角線上的元素都是「1」。 在矩陣H3中，所述k個矩陣H5之外的元素均為「0」，所述k個矩陣H5中第i個矩陣等於矩陣H3中第(i-1)×L+1行至i×L行與第(i-1)×L2+1列至第i×L2列對應的矩陣，i的取值範圍為1至k中的所有整數。

第二種情況：m/3＝k×L+r且k為正整數、r為1至L-1範圍內的正整數，即m/3不能夠被L整除。

在第二種情況下，矩陣H可以表示為：

具體地，矩陣H由矩陣H1』、矩陣H2』和矩陣H3』組成，矩陣H1』構成矩陣H的第1行至第m/3行，矩陣H2』構成矩陣H的第m/3+1行至第2m/3行，矩陣H3』構成矩陣H的第2m/3+1行至第m行，矩陣H1』、矩陣H2』和矩陣H3』均為(k×L+r)×(k×L2+r×L)維的矩陣。

矩陣H1』可以按照如下方式來構造：

在矩陣H1』中，每行中元素「1」的數量等於L，每列中元素「1」的數量等於1，每行中的L個元素「1」是連續的。

矩陣H2』可以按照如下方式來構造：

在矩陣H2』中，每行中元素「1」的數量等於L，每列中元素「1」的數量等於1，矩陣H2』由L個矩陣H4』組成，矩陣H4』為(k×L+r)×(k×L+r)維的對角陣，矩陣H4』的主對角線上的元素都是「1」。

矩陣H3』是將矩陣H5』中第k×L2+b×L+c列與第b×L2+(c-1)×L+c列進行位 置互換而得到的，b的取值範圍為0至r-1內的所有整數，c的取值範圍為1至L內的所有整數。

矩陣H5』可以按照如下方式來構造：

矩陣H5』中第1行至k×L行與第1列至k×L2列對應的矩陣等於矩陣H6』，矩陣H5』中第k×L+1行至第k×L+r行與第k×L2+1列至k×L2+r×L列對應的矩陣等於矩陣H7』，矩陣H5』中矩陣H6』和矩陣H7』之外的元素均為「0」。

矩陣H6』為(k×L)×(k×L2)維的矩陣，矩陣H7』為r×(r×L)維的矩陣。矩陣H6』等於矩陣H3。在矩陣H7』中，每行中元素「1」的數量為L，每列中元素「1」的數量等於1，每行的L個元素「1」是連續的。

可選的，在一些實施方式中，所述LDPC校驗矩陣為所述矩陣H。

可選的，在另一些實施方式中，所述LDPC校驗矩陣是對所述矩陣H進行隨機行置換和/或隨機列置換而得到的。

需要說明的是，本實施例中，矩陣H、LDPC校驗矩陣可以採用圖4所示實施例中提及方式進行構造，具體可參見前述圖4所示的實施例的相關內容，本實施例在此不再贅述。

通過本實施例的技術方案，無論是上述第一種情況還是上述第二種情況，m×n維的矩陣H都是由三個(m/3)×n維的子矩陣組成，在這三個子矩陣中，每行中元素「1」的數量為L，每列中元素「1」的數量為1，並且，這三個子矩陣的取值範圍是各不相同的，這使得矩陣H中任意兩行與任意兩列的四個交匯處的元素均至少存在一個「0」，保證矩陣H對應的TG的圍長大於4，因此，基於矩陣H生成LDPC校驗矩陣，就可以保證LDPC校驗矩陣對應的TG的圍長大於4，因此，採用這樣的LDPC校驗矩陣對數據進行解碼，當傳輸中的LDPC碼的信噪比比較低時，對接收到的LDPC碼進行解碼得到的數據的的誤比特率較低，因此，LDPC碼的性能得以提高。

圖9為本發明實施例中一種基於校驗矩陣的裝置900的結構示意圖。所述裝置900具體包括：

獲取單元901，用於獲取數據；

生成單元902，用於通過利用低密度奇偶校驗LDPC校驗矩陣對所述獲取單元901獲取到的所述數據進行編碼，生成編碼數據。

舉例來說，圖9所示的基於校驗矩陣的設備可以用於執行圖4所示的方法。具體地，獲取單元901可以用於執行圖4中的步驟401。生成單元902可以用於執行圖4中的步驟402。

具體實現時，獲取單元901可以以比特串的形式對數據進行獲取，生成單元902可以以比特串的形式對數據進行編碼。在編碼器900中，獲取單元901獲取一個比特串，生成單元902利用LDPC校驗矩陣對該比特串進行編碼，從而生成一個編碼比特串。該編碼比特串可以用於在實際數據鏈路中傳輸。其中，所述裝置900例如可以實現為編碼器、處理器晶片等。所述獲取單元901例如可以實現為接收器、存儲器等獲取電路。所述生成單元902例如可以實現為編碼電路。

在本實施例中，用於編碼的LDPC校驗矩陣是基於矩陣H生成的。在矩陣H中，每行中元素「1」的數量為L，每列中元素「1」的數量為3，矩陣H為m×n維的矩陣。其中，本實施例可以採用下述第一種情況的矩陣H，或者，也可以採用下述第二種情況的矩陣H。

第一種情況：m/3＝k×L且k為正整數，即m/3能夠被L整除。

在第一種情況下，矩陣H可以表示為：

具體地，矩陣H由矩陣H1、矩陣H2和矩陣H3組成，矩陣H1構成矩陣H的第1行至第m/3行，矩陣H2構成矩陣H的第m/3+1行至第2m/3行，矩陣H3構成矩陣H的第2m/3+1行至第m行，矩陣H1、矩陣H2和矩陣H3均為(k×L)×(k×L2)維的矩陣。

矩陣H1可以按照如下方式來構造：

在矩陣H1中，每行中元素「1」的數量等於L，每列中元素「1」的數量等於1，每行中的L個元素「1」是連續的。

矩陣H2可以按照如下方式來構造：

在矩陣H2中，每行中元素「1」的數量等於L，每列中元素「1」的數量等於1，矩陣H2由L個矩陣H4組成，矩陣H4為(k×L)×(k×L)維的對角陣，矩陣H4的主對角線上的元素都是「1」。

矩陣H3可以按照如下方式來構造：

在矩陣H3中，每行中的元素「1」的數量為L，每列中的元素「1」的數量為1，矩陣H3包括k個矩陣H5，矩陣H5包括L個矩陣H6，矩陣H5為L×L2維的矩陣，矩陣H6為L×L維的對角陣，矩陣H6的主對角線上的元素都是「1」。在矩陣H3中，所述k個矩陣H5之外的元素均為「0」，所述k個矩陣H5中第i個矩陣等於矩陣H3中第(i-1)×L+1行至i×L行與第(i-1)×L2+1列至第i×L2列對應的矩陣，i的取值範圍為1至k中的所有整數。

第二種情況：m/3＝k×L+r且k為正整數、r為1至L-1範圍內的正整數，即m/3不能夠被L整除。

在第二種情況下，矩陣H可以表示為：

具體地，矩陣H由矩陣H1』、矩陣H2』和矩陣H3』組成，矩陣H1』構成矩陣H的第1行至第m/3行，矩陣H2』構成矩陣H的第m/3+1行至第2m/3行，矩陣H3』構成矩陣H的第2m/3+1行至第m行，矩陣H1』、矩陣H2』和矩陣H3』均為(k×L+r)×(k×L2+r×L)維的矩陣。

矩陣H1』可以按照如下方式來構造：

在矩陣H1』中，每行中元素「1」的數量等於L，每列中元素「1」的數量等於1，每行中的L個元素「1」是連續的。

矩陣H2』可以按照如下方式來構造：

在矩陣H2』中，每行中元素「1」的數量等於L，每列中元素「1」的數量等於1，矩陣H2』由L個矩陣H4』組成，矩陣H4』為(k×L+r)×(k×L+r)維的對角陣，矩陣H4』的主對角線上的元素都是「1」。

矩陣H3』是將矩陣H5』中第k×L2+b×L+c列與第b×L2+(c-1)×L+c列進行位置互換而得到的，b的取值範圍為0至r-1內的所有整數，c的取值範圍為1至L內的所有整數。

矩陣H5』可以按照如下方式來構造：

矩陣H5』中第1行至k×L行與第1列至k×L2列對應的矩陣等於矩陣H6』，矩陣H5』中第k×L+1行至第k×L+r行與第k×L2+1列至k×L2+r×L列對應的矩陣等於矩陣H7』，矩陣H5』中矩陣H6』和矩陣H7』之外的元素均為「0」。

矩陣H6』為(k×L)×(k×L2)維的矩陣，矩陣H7』為r×(r×L)維的矩陣。矩陣H6』等於矩陣H3。在矩陣H7』中，每行中元素「1」的數量為L，每列中元素「1」的數量等於1，每行的L個元素「1」是連續的。

可選的，在一些實施方式中，所述LDPC校驗矩陣為所述矩陣H。

可選的，在另一些實施方式中，所述LDPC校驗矩陣是對所述矩陣H進行隨機行置換和/或隨機列置換而得到的。

需要說明的是，本實施例中，矩陣H的構造、LDPC校驗矩陣的構造，具體可參見前述圖4所示的實施例的相關內容，本實施例在此不再贅述。

通過本實施例的技術方案，可以保證矩陣H對應的TG的圍長大於4，因此，基於矩陣H生成LDPC校驗矩陣，就可以保證LDPC校驗矩陣對應的TG的圍長大於4，因此，裝置900採用這樣的LDPC校驗矩陣對數據進行編碼，當傳輸中的LDPC碼的信噪比比較低時，對接收到的LDPC碼進行解碼得到的數據的的誤比特率較低，因此，LDPC碼的性能得以提高。

圖10為本發明實施例中一種基於校驗矩陣的裝置1000的結構示意圖。所述裝置1000包括：

獲取單元1001，用於獲取編碼數據；

生成單元1002，用於通過利用低密度奇偶校驗LDPC校驗矩陣對所述獲取單元1002獲取到的所述編碼數據進行解碼，生成數據，所述LDPC校驗矩陣是基於矩陣H生成的，在矩陣H中，每行中元素「1」的數量為L，每列中元素「1」的數量為3；矩陣H為m×n維的矩陣。

圖10所示的基於校驗矩陣的設備可以用於執行圖8所示的方法。具體地， 獲取單元1001可以用於執行圖8中的步驟801。生成單元1002可以用於執行圖8中的步驟802。

具體實現時，獲取單元1001可以以比特串的形式對數據進行獲取，生成單元1002可以以比特串的形式對數據進行解碼。在解碼器1000中，獲取單元1001獲取一個編碼比特串，生成單元1002利用LDPC校驗矩陣對該編碼比特串進行解碼，從而生成一個比特串。該編碼比特串可以用於在實際數據鏈路中傳輸。其中，所述裝置1000例如可以實現為解碼器、處理器晶片等。所述獲取單元1001例如可以實現為接收器、存儲器等獲取電路。所述生成單元1002例如可以實現為解碼電路。在本實施例中，用於解碼的LDPC校驗矩陣是基於矩陣H生成的。在矩陣H中，每行中元素「1」的數量為L，每列中元素「1」的數量為3，矩陣H為m×n維的矩陣。其中，本實施例可以採用下述第一種情況的矩陣H，或者，也可以採用下述第二種情況的矩陣H。

第一種情況：m/3＝k×L且k為正整數，即m/3能夠被L整除。

在第一種情況下，矩陣H可以表示為：

具體地，矩陣H由矩陣H1、矩陣H2和矩陣H3組成，矩陣H1構成矩陣H的第1行至第m/3行，矩陣H2構成矩陣H的第m/3+1行至第2m/3行，矩陣H3構成矩陣H的第2m/3+1行至第m行，矩陣H1、矩陣H2和矩陣H3均為(k×L)×(k×L2)維的矩陣。

矩陣H1可以按照如下方式來構造：

在矩陣H1中，每行中元素「1」的數量等於L，每列中元素「1」的數量等於1，每行中的L個元素「1」是連續的。

矩陣H2可以按照如下方式來構造：

在矩陣H2中，每行中元素「1」的數量等於L，每列中元素「1」的數量等於1，矩陣H2由L個矩陣H4組成，矩陣H4為(k×L)×(k×L)維的對角陣，矩陣H4的主對角線上的元素都是「1」。

矩陣H3可以按照如下方式來構造：

在矩陣H3中，每行中的元素「1」的數量為L，每列中的元素「1」的數量為1，矩陣H3包括k個矩陣H5，矩陣H5包括L個矩陣H6，矩陣H5為L×L2維的矩陣，矩陣H6為L×L維的對角陣，矩陣H6的主對角線上的元素都是「1」。在矩陣H3中，所述k個矩陣H5之外的元素均為「0」，所述k個矩陣H5中第i個矩陣等於矩陣H3中第(i-1)×L+1行至i×L行與第(i-1)×L2+1列至第i×L2列對應的矩陣，i的取值範圍為1至k中的所有整數。

第二種情況：m/3＝k×L+r且k為正整數、r為1至L-1範圍內的正整數，即m/3不能夠被L整除。

在第二種情況下，矩陣H可以表示為：

具體地，矩陣H由矩陣H1』、矩陣H2』和矩陣H3』組成，矩陣H1』構成矩陣H的第1行至第m/3行，矩陣H2』構成矩陣H的第m/3+1行至第2m/3行，矩陣H3』構成矩陣H的第2m/3+1行至第m行，矩陣H1』、矩陣H2』和矩陣H3』均為(k×L+r)×(k×L2+r×L)維的矩陣。

矩陣H1』可以按照如下方式來構造：

在矩陣H1』中，每行中元素「1」的數量等於L，每列中元素「1」的數量等於1，每行中的L個元素「1」是連續的。

矩陣H2』可以按照如下方式來構造：

在矩陣H2』中，每行中元素「1」的數量等於L，每列中元素「1」的數量等於1，矩陣H2』由L個矩陣H4』組成，矩陣H4』為(k×L+r)×(k×L+r)維的對角陣，矩陣H4』的主對角線上的元素都是「1」。

矩陣H3』是將矩陣H5』中第k×L2+b×L+c列與第b×L2+(c-1)×L+c列進行位置互換而得到的，b的取值範圍為0至r-1內的所有整數，c的取值範圍為1至L內的所有整數。

矩陣H5』可以按照如下方式來構造：

矩陣H5』中第1行至k×L行與第1列至k×L2列對應的矩陣等於矩陣H6』，矩陣H5』中第k×L+1行至第k×L+r行與第k×L2+1列至k×L2+r×L列對應的矩陣等於矩陣H7』，矩陣H5』中矩陣H6』和矩陣H7』之外的元素均為「0」。

矩陣H6』為(k×L)×(k×L2)維的矩陣，矩陣H7』為r×(r×L)維的矩陣。矩陣H6』等於矩陣H3。在矩陣H7』中，每行中元素「1」的數量為L，每列中元素「1」的數量等於1，每行的L個元素「1」是連續的。

可選的，在一些實施方式中，所述LDPC校驗矩陣為所述矩陣H。

可選的，在另一些實施方式中，所述LDPC校驗矩陣是對所述矩陣H進行隨機行置換和/或隨機列置換而得到的。

需要說明的是，本實施例中，矩陣H的構造、LDPC校驗矩陣的構造，具體可參見前述圖4所示的實施例的相關內容，本實施例在此不再贅述。

通過本實施例的技術方案，可以保證矩陣H對應的TG的圍長大於4，因此，基於矩陣H生成LDPC校驗矩陣，就可以保證LDPC校驗矩陣對應的TG的圍長大於4，因此，解碼器1000採用這樣的LDPC校驗矩陣對數據進行解碼，當傳輸中的LDPC碼的信噪比比較低時，對接收到的LDPC碼進行解碼得到的數據的的誤比特率較低，因此，LDPC碼的性能得以提高。

圖11為本發明實施例中一種編碼器的結構示意圖。在本實施例中，編碼器1100包括：處理器1101、存儲器1102、網絡接口1103、總線系統1104。

所述總線系統1104，用於將編碼器設備1100的各個硬體組件耦合在一起。

所述網絡接口1103，用於實現編碼器設備1100與至少一個其它網元之間的通信連接，可以使用網際網路，廣域網，本地網，城域網等方式。

所述存儲器1102，用於存儲程序指令和數據。

所述處理器1101，用於讀取存儲器1102中存儲的指令和數據，執行以下操作：

處理器1101獲取數據；以及

處理器1101通過利用低密度奇偶校驗矩陣LDPC校驗矩陣對所述數據進行編碼，生成編碼數據，所述LDPC校驗矩陣是基於矩陣H生成的，在矩陣H中，每行中元素「1」的數量為L，每列中元素「1」的數量為3，矩陣H為m×n維的矩陣；

m/3＝k×L且k為正整數，矩陣H由矩陣H1、矩陣H2和矩陣H3組成，矩陣H1構成矩陣H的第1行至第m/3行，矩陣H2構成矩陣H的第m/3+1行至第2m/3行，矩陣H3構成矩陣H的第2m/3+1行至第m行，矩陣H1、矩陣H2和矩陣H3均為(k×L)×(k×L2)維的矩陣；

其中，

在矩陣H1中，每行中元素「1」的數量等於L，每列中元素「1」的數量等於1，每行中的L個元素「1」是連續的；

在矩陣H2中，每行中元素「1」的數量等於L，每列中元素「1」的數量等於1，矩陣H2由L個矩陣H4組成，矩陣H4為(k×L)×(k×L)維的對角陣，矩陣H4的主對角線上的元素都是「1」；

在矩陣H3中，每行中的元素「1」的數量為L，每列中的元素「1」的數量為1，矩陣H3包括k個矩陣H5，矩陣H5包括L個矩陣H6，矩陣H5為L×L2維的矩陣，矩陣H6為L×L維的對角陣，矩陣H6的主對角線上的元素都是「1」；

在矩陣H3中，所述k個矩陣H5之外的元素均為「0」，所述k個矩陣H5中第i個矩陣等於矩陣H3中第(i-1)×L+1行至i×L行與第(i-1)×L2+1列至第i×L2列對應的矩陣，i的取值範圍為1至k中的所有整數；

或者，

m/3＝k×L+r且k為正整數、r為1至L-1範圍內的正整數，矩陣H由矩陣H1』、矩陣H2』和矩陣H3』組成，矩陣H1』構成矩陣H的第1行至第m/3行，矩陣H2』構成矩陣H的第m/3+1行至第2m/3行，矩陣H3』構成矩陣H的第2m/3+1行至第m行，矩陣H1』、矩陣H2』和矩陣H3』均為(k×L+r)×(k×L2+r×L)維的矩陣；

其中，

在矩陣H1』中，每行中元素「1」的數量等於L，每列中元素「1」的數量等於1，每行中的L個元素「1」是連續的；

在矩陣H2』中，每行中元素「1」的數量等於L，每列中元素「1」的數量等於1，矩陣H2』由L個矩陣H4』組成，矩陣H4』為(k×L+r)×(k×L+r)維的對角陣，矩陣H4』的主對角線上的元素都是「1」；

矩陣H3』是將矩陣H5』中第k×L2+b×L+c列與第b×L2+(c-1)×L+c列進行位置互換而得到的，b的取值範圍為0至r-1內的所有整數，c的取值範圍為1至L內的所有整數；

矩陣H5』中第1行至k×L行與第1列至k×L2列對應的矩陣等於矩陣H6』，矩陣H5』中第k×L+1行至第k×L+r行與第k×L2+1列至k×L2+r×L列對應的矩陣等於矩陣H7』，矩陣H5』中矩陣H6』和矩陣H7』之外的元素均為「0」；

矩陣H6』為(k×L)×(k×L2)維的矩陣，矩陣H7』為r×(r×L)維的矩陣，矩陣H6』等於矩陣H3，在矩陣H7』中，每行中元素「1」的數量為L，每列中元素「1」的數量等於1，每行的L個元素「1」是連續的。

可選的，處理器1101採用的所述LDPC校驗矩陣，例如可以為矩陣H。

可選的，處理器1101採用的所述LDPC校驗矩陣，例如可以是對矩陣H 進行行置換和/或列置換而得到的。

圖11所示的編碼器可以用於實現圖9所示的基於校驗矩陣的裝置。另外，圖11所示的編碼器可以用於執行圖4所示的方法。

圖12為本發明實施例中一種解碼器的結構示意圖。在本實施例中，解碼器1200包括：處理器1201、存儲器1202、網絡接口1203、總線系統1204。

所述總線系統1204，用於將解碼器設備1200的各個硬體組件耦合在一起。

所述網絡接口1203，用於實現解碼器設備1200與至少一個其它網元之間的通信連接，可以使用網際網路，廣域網，本地網，城域網等方式。

所述存儲器1202，用於存儲程序指令和數據。

所述處理器1201，用於讀取存儲器1202中存儲的指令和數據，執行以下操作：

處理器1201獲取編碼數據；以及

處理器1201通過利用低密度奇偶校驗LDPC校驗矩陣對所述編碼數據進行解碼，生成數據，所述LDPC校驗矩陣是基於矩陣H生成的，在矩陣H中，每行中元素「1」的數量為L，每列中元素「1」的數量為3，矩陣H為m×n維的矩陣；

m/3＝k×L且k為正整數，矩陣H由矩陣H1、矩陣H2和矩陣H3組成，矩陣H1構成矩陣H的第1行至第m/3行，矩陣H2構成矩陣H的第m/3+1行至第2m/3行，矩陣H3構成矩陣H的第2m/3+1行至第m行，矩陣H1、矩陣H2和矩陣H3均為(k×L)×(k×L2)維的矩陣；

其中，

在矩陣H1中，每行中元素「1」的數量等於L，每列中元素「1」的數量等於1，每行中的L個元素「1」是連續的；

在矩陣H2中，每行中元素「1」的數量等於L，每列中元素「1」的數量等於1，矩陣H2由L個矩陣H4組成，矩陣H4為(k×L)×(k×L)維的對角陣，矩陣H4的主對角線上的元素都是「1」；

在矩陣H3中，每行中的元素「1」的數量為L，每列中的元素「1」的數量為1，矩陣H3包括k個矩陣H5，矩陣H5包括L個矩陣H6，矩陣H5為L×L2維的矩陣，矩陣H6為L×L維的對角陣，矩陣H6的主對角線上的元素都是「1」；

在矩陣H3中，所述k個矩陣H5之外的元素均為「0」，所述k個矩陣H5中第i個矩陣等於矩陣H3中第(i-1)×L+1行至i×L行與第(i-1)×L2+1列至第i×L2列對應的矩陣，i的取值範圍為1至k中的所有整數；

或者，

m/3＝k×L+r且k為正整數、r為1至L-1範圍內的正整數，矩陣H由矩陣H1』、矩陣H2』和矩陣H3』組成，矩陣H1』構成矩陣H的第1行至第m/3行，矩陣H2』構成矩陣H的第m/3+1行至第2m/3行，矩陣H3』構成矩陣H的第2m/3+1行至第m行，矩陣H1』、矩陣H2』和矩陣H3』均為(k×L+r)×(k×L2+r×L)維的矩陣；

其中，

在矩陣H1』中，每行中元素「1」的數量等於L，每列中元素「1」的數量等於1，每行中的L個元素「1」是連續的；

在矩陣H2』中，每行中元素「1」的數量等於L，每列中元素「1」的數量等於1，矩陣H2』由L個矩陣H4』組成，矩陣H4』為(k×L+r)×(k×L+r)維的對角陣，矩陣H4』的主對角線上的元素都是「1」；

矩陣H3』是將矩陣H5』中第k×L2+b×L+c列與第b×L2+(c-1)×L+c列進行位置互換而得到的，b的取值範圍為0至r-1內的所有整數，c的取值範圍為1至L內的所有整數；

矩陣H5』中第1行至k×L行與第1列至k×L2列對應的矩陣等於矩陣H6』，矩陣H5』中第k×L+1行至第k×L+r行與第k×L2+1列至k×L2+r×L列對應的矩陣等於矩陣H7』，矩陣H5』中矩陣H6』和矩陣H7』之外的元素均為「0」；

矩陣H6』為(k×L)×(k×L2)維的矩陣，矩陣H7』為r×(r×L)維的矩陣，矩陣H6』等於矩陣H3，在矩陣H7』中，每行中元素「1」的數量為L，每列中元素「1」的數量等於1，每行的L個元素「1」是連續的。

可選的，處理器1201採用的所述LDPC校驗矩陣，例如可以為矩陣H。

可選的，處理器1201採用的所述LDPC校驗矩陣，例如可以是對矩陣H進行行置換和/或列置換而得到的。

圖12所示的解碼器可以用於實現圖10所示的基於校驗矩陣的裝置另外，圖12所示的解碼器可以用於執行圖8所示的方法。

需要說明的是，本發明實施例中的處理器可能是一種集成電路晶片，具有信號的處理能力。在實現過程中，上述方法的各步驟可以通過處理器中的硬體的集成邏輯電路或者軟體形式的指令完成。這些指令可以通過其中的處 理器以配合實現及控制，用於執行本發明實施例揭示的方法。上述處理器還可以是通用處理器、數位訊號處理器(Digital Signal Processing，DSP)、專用集成電路(application specific integrated circuit)、現成可編程門陣列(Field Programmable Gate Array，FPGA)或者其他可編程邏輯器件、分立門或者電晶體邏輯器件、分立硬體組件。

其中，上述通用處理器可以是微處理器或者該處理器也可以是任何常規的處理器，解碼器等。結合本發明實施例所公開的方法的步驟可以直接體現為硬體處理器執行完成，或者用處理器中的硬體及軟體模塊組合執行完成。軟體模塊可以位於隨機存儲器，快閃記憶體、只讀存儲器，可編程只讀存儲器或者電可擦寫可編程存儲器、寄存器等本領域成熟的存儲介質中。

另外，需要說明的是，總線系統除了包括數據總線之外，還可包括電源總線、控制總線和狀態信號總線。但是為了清楚說明起見，在圖8、9中將各種總線都標為總線系統。

通過以上的實施方式的描述可知，本領域的技術人員可以清楚地了解到上述實施例方法中的全部或部分步驟可藉助軟體加通用硬體平臺的方式來實現。基於這樣的理解，本發明的技術方案本質上或者說對現有技術做出貢獻的部分可以以軟體產品的形式體現出來，該計算機軟體產品可以存儲在存儲介質中，如ROM/RAM、磁碟、光碟等，包括若干指令用以使得一臺計算機設備(可以是個人計算機，伺服器，或者諸如媒體網關等網絡通信設備)執行本發明各個實施例或者實施例的某些部分所述的方法。

需要說明的是，本說明書中的各個實施例均採用遞進的方式描述，各個實施例之間相同相似的部分互相參見即可，每個實施例重點說明的都是與其他實施例的不同之處。尤其，對於方法實施例和設備實施例而言，由於其基本相似於系統實施例，所以描述得比較簡單，相關之處參見系統實施例的部分說明即可。以上所描述的設備及系統實施例僅僅是示意性的，其中作為分離部件說明的模塊可以是或者也可以不是物理上分開的，作為模塊顯示的部件可以是或者也可以不是物理模塊，即可以位於一個地方，或者也可以分布到多個網絡單元上。可以根據實際的需要選擇其中的部分或者全部模塊來實現本實施例方案的目的。本領域普通技術人員在不付出創造性勞動的情況下， 即可以理解並實施。

以上所述僅是本發明的優選實施方式，並非用於限定本發明的保護範圍。應當指出，對於本技術領域的普通技術人員來說，在不脫離本發明原理的前提下，還可以作出若干改進和潤飾，這些改進和潤飾也應視為本發明的保護範圍。