一種集總參數射頻電感模型及其優化設計方法與流程
2023-05-22 05:37:16 1
本發明屬於微波技術、微波電路領域,具體涉及一種集總參數射頻電感模型
背景技術:
單片微波集成電路已被用於許多高頻個人通信產品。由於矽集成技術具有應用面廣,集成度高和成本低的特點,隨著研究的深入,許多早期的微波器件的頻率限制已被克服。因此,現在矽集成技術在越來越多的射頻和微波應用中使用。典型的應用包括低噪聲放大器,混頻器,射頻開關,功率放大器和電壓控制振蕩器等。由於集總元件具有小尺寸的特性,它們在集成電路中的應用是非常普遍的。對於標準的矽技術,因為它具有高的襯底損耗和使用電阻率較高的鋁、銅及較薄的金屬厚度,因此標準矽技術製造一個較高的品質因數電感是一個艱巨的任務。然而,它的低成本和在的混合集成方面的應用使矽技術對許多射頻集成電路具有非常大的吸引力。通過許多研究人員對矽射頻電感的研究,在矽射頻電感的建模方面取得了很大的進展,但仍然存在一些有待改進的方面。比如有些模型的使用限制較多,有些模型對電感值的計算精度不高,以及有些模型採用的計算過程和方法不便於電路優化。
技術實現要素:
本發明的目的是為了解決矽射頻電感值的計算精度不高及不便於電路優化的局限,而提出一種有效提高矽射頻電感值的計算精度和便於實現電路優化的矽射頻電感模型。
本發明採用的技術方案如下:
一種集總參數射頻電感模型,由串聯電感1、串聯導體等效電阻2、引出電容3、氧化物層電容4、襯底電容5及襯底電阻6構成,其特徵在於,串聯電感1一端接串聯導體等效電阻2,另一端為輸出負極;串聯導體等效電阻2另一端為輸出正極;引出電容3一端接輸出正極另一端接輸出負極;氧化物層電容4一端接輸出正極另一端接襯底電容5和襯底電阻6;襯底電容和襯底電阻另一端接輸出負極。
所述串聯電感為片上電感的電感值,採用帶校正因子的公式對其進行計算:
其中b=(n-1)(w+s)+w,dm=din+b,K為校正因子,n為線圈的圈數,w為金屬導體的寬度,S為線圈之間的間距,din金屬導體的內徑,t金屬導體的厚度。
所述串聯導體等效電阻由金屬導體的趨膚效應形成的,具體的計算公式如下:
其中w為金屬導體的寬度,ρ為金屬的電阻率,δ為金屬的導體的趨膚厚度,t為金屬導體的厚度,f為電感的工作頻率。當δ大於t時,其取值為t。
所述引出電容由下層終端引出結點與上層金屬之間的電勢差形成,其計算公式如下:
其中εox和toxM1-M2分別為電感層和終端引出層間介質的介電常數、厚度。
所述氧化物層電容電感層與襯底層之間由於絕緣介質的存在而形成的,其計算公式如下:
其中l和tox分別為電感的長度、電感層與襯底層間絕緣介質的厚度。
進一步的,所述襯底電容及襯底電阻由襯底的寄生參量構成,模擬了襯底的損耗,其計算公式如下:
Csi=1/2·l·w·Csub
其中Csub、Gsub是矽襯底的單位電容、電導,它們的值可由測量數據獲得。
本發明的目的還在於,在上述模型的基礎上建立一種集總參數射頻電感模型優化設計方法,其具體手段為:
A.設置優化目標函數:在一般情況下,電感的優化目標函數是電感值L和品質因數Q。
L=Im[Z11]/ω,Q=Im[Z11]/Re[Z11]
阻抗Z11可以從物理電路模型獲得。如果應用電路設計軟體如ADS,則Z11可以簡單地從S11獲得:
B.在此物理電路模型中,只有兩個參數需要從測量數據或其他方法(如電磁場軟體)提取,即Csub和Gsub。首先以0.8作為校正因子的初始值,根據優化目標函數得到初始優化電感結構。
C.用格林豪斯算法獲得準確的電感值,最後與模型值比較,得到實際校正因子的值。
D.利用上一步得到的校正因子的值進行優化,確定最終幾何結構尺寸。
採用本發明的模型和方法有益效果是,帶校正因子的電感計算公式,便於使用專業軟體進行優化設計。採用一埠物理電路模型,便於使電感的優化目標函數和其幾何尺寸建立聯繫,簡化電感優化設計步驟。考慮趨夫厚度與導體厚度的關係提高計算的精度。通過大量實例的研究確定了校正因子的初始值,減少了優化步驟。用格林豪斯算法獲得準確的電感值,以此得到實際校正因子提高設計精度。本發明有效解決了矽射頻電感值的計算精度不高及不便於電路優化的問題,為提高矽射頻電感的計算精度和便於實現矽射頻電感優化設計,提供了一種有力的手段。
附圖說明
圖1為矽射頻電感一埠物理電路模型;
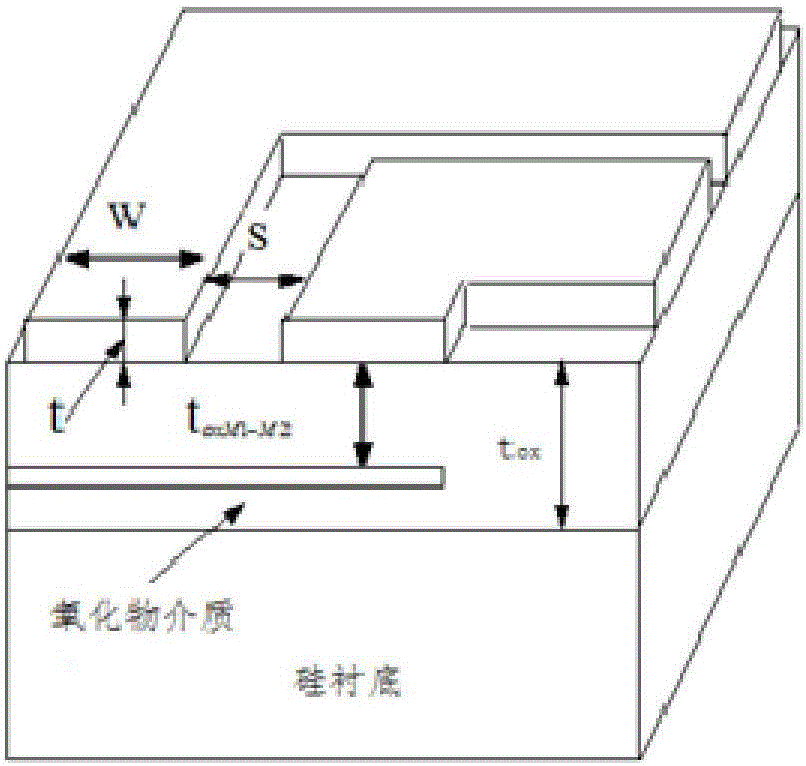
圖2為矽射頻電感幾何結構示意圖;
圖3為實施例模型計算、測量及3維電磁軟體計算所得散射參數對比圖;
圖4為實施例模型計算和測量所得電感值和品質因數對比圖;
具體實施方式
下面結合附圖與具體實施方式對本發明作進一步的描述:
實施例
本實施例以矽射頻電感一埠物理電路模型為例進行說明
如圖1所示,本例矽射頻電感一埠物理電路模型,包括串聯電感1、串聯導體等效電阻2、引出電容3、氧化物層電容4、襯底電容5及襯底電阻6。本例矽射頻電感幾何結構示意圖如圖2所示,w為金屬導體的寬度,S為線圈之間的間距,t為金屬導體的厚度,toxM1-M2為電感層和終端引出層間介質的厚度,tox為電感層與襯底層間絕緣介質的厚度。本例矽電感結構參數如下:金屬導體為鋁,襯底電阻率為10Ohm-cm,εox=3.9,t=1.2um,toxm1-2=3um,tox=5um,n=3,W=7um,S=2um,電感總長l=1548um,電感內直徑din=98um.
在本實施例中,首先令校正因子為0.8,然後採用物理電路模型中的計算公式優化設計出電感的幾何尺寸。其次用格林豪斯算法獲得準確的電感值,最後與模型值比較,得到實際校正因子的值。最後用得到的校正因子的值進行優化,確定最終電感幾何結構尺寸。
模型計算、測量及3維電磁軟體計算所得散射參數對比如圖3所示,三種方法得到的散射參數吻合很好。圖4為實施例模型計算和測量所得電感值和品質因數對比圖,在電感諧振頻率以下,二者吻合較好,其中電感值的誤差小於7%,品質因數的誤差小於6%。
從實施例可以看出,本發明的矽電感物理電路模型能方便地用於矽電感的優化設計,在提高矽射頻電感值的計算精度和簡化電路優化程序方面具有很大的實際應用價值。
上述實施例為本發明較佳的實施方式,但本發明的實施方式並不受上述實施例的限制,其他的任何未背離本發明的精神實質與原理下所作的改變、修飾、替代、組合、簡化,均應為等效的置換方式,都包含在本發明的保護範圍之內。
