一種可重構系統貝葉斯網構建方法與流程

2023-05-14 10:11:24 2

本發明涉及一種可重構系統貝葉斯網構建方法，適用於可重構系統的貝葉斯網構建，進而可支持裝備的故障診斷推理。

背景技術：

故障診斷對裝備的正常安全運行至關重要。貝葉斯網作為一種信度網絡，在不確定性知識表達和推理領域具有較強的能力，已在故障診斷方面取得了成功的應用。然而，貝葉斯網的構建一直以來都是非常困難的事情，需要大量的專家知識，是非常耗時耗力的工作，限制了其在大規模系統中的應用。當前，貝葉斯網的構建以人工為主，面向的主要是單模式小規模系統，缺乏一種系統性的自動化方法。尤其是針對可重構系統而言，由於系統結構在應用過程中會發生變化，貝葉斯網的表達比較困難，當前缺乏一種工程中適用的貝葉斯網構建方法。

技術實現要素：

本發明的目的是提供一種適用於可重構系統的貝葉斯網構建方法，為基於貝葉斯網的故障診斷提供支持。

為達到上述目的，本發明提供了以下解決方案：1、一種可重構系統貝葉斯網構建方法，包括以下步驟：

(1)對可重構系統故障和測試的相關性建立模型；

(2)對可重構系統故障和測試的相關性進行表徵；

(3)確定可重構系統貝葉斯網結構；

(4)確定重構系統貝葉斯網參數並採用樹形結構進行表徵。

進一步的，所述步驟(1)中的模型包含四種元素，分別為故障、開關、測試點以及用來連接故障、測試點及開關的連接線；該模型的工作方式為：當故障和測試之間有連接通路，則故障和測試點之間相關，否則不相關；所述故障和測試之間可設置開關，通過開關的啟閉影響故障和測試之間的相關性，進而實現系統的重構。

進一步的，步驟(2)中故障和測試的相關性用矩陣d1表示，d1＝[dij]m×n，其中dij∈{0,1}，取值為0表示第j個測試在任意模式下均無法檢測到第i個故障，取值為1表示第j個測試可檢測到第i個故障；所述測試和開關的相關性用矩陣d2進行表示，d2＝[rij]n×k，其中rij∈{0,1}，取值為0表示第j個測試和故障的相關性不受第i個開關狀態的影響，取值為1表示第j個測試和故障的相關性和第i個開關的狀態相關；其中，m表示故障的個數，n表示測試的個數，k表示開關的個數。

進一步的，步驟(3)中的貝葉斯網包括兩層結構組成，第一層由故障和開關節點組成，第二層由測試節點組成。

進一步的，步驟(3)中的貝葉斯網節點之間的連接關係和步驟(2)中的矩陣對應，針對矩陣d1＝[dij]m×n，如果dij＝1，則在第i個故障和第j個測試之間添加連接關係，方向由fi指向tj；針對矩陣d2＝[rij]n×k，如果rij＝1，則在第j個測試和第i個開關之間添加連接關係，方向由si指向tj；其中，所述第i個故障用fi表示，所述第j個測試用tj表示，所述第i個開關用si表示。

進一步的，步驟(4)中測試節點貝葉斯網參數採用二叉樹表達，並採用優化方式生成。

進一步的，所述優化方法包括以下步驟：

ⅰ，針對某一個測試節點，用集合e＝{f,s}表示初始備選節點集，其中f表示與其相關的故障節點，s表示與其相關的開關節點；

ⅱ，從集合e中選擇相關故障節點數目最多且不為0的開關節點作為下一步的樹節點；針對開關閉合分枝，從e中去除該開關節點；針對開關斷開這一分枝，從e中去除該開關節點以及和該開關相關的故障節點，更新e；若集合e中無開關節點，轉步驟ⅲ；

ⅲ，選擇故障率最高的故障節點作為下一步的樹節點，從e中去除該故障節點，更新e；針對故障存在這一分枝，存儲參數1，停止擴展該分枝；針對故障不存在這一分枝，若e中不包含其它故障節點，存儲參數0，否則，繼續選擇步驟ⅱ，擴展參數表達樹；

ⅳ，最終所得的二叉樹即為測試節點的參數。

本發明的有益效果是：提出了一種程序化的可重構系統貝葉斯網構建方法，對貝葉斯網參數存儲和檢索進行了優化，為解決可重構系統貝葉斯網構建問題提供了一條新的解決途徑，可促進貝葉斯網在故障診斷領域的應用。

附圖說明

為了易於說明，本發明由下述的具體實施、實施例及附圖作以詳細描述。

圖1為本發明實施例中可重構系統的相關性模型；

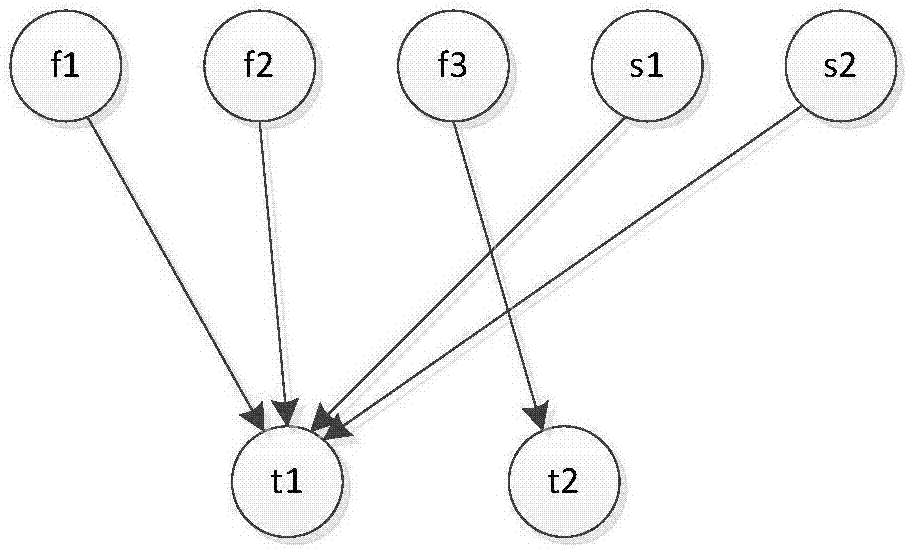
圖2為本發明實施例中可重構系統構建的貝葉斯網；

圖3為實施例中所構建的貝葉斯網t1節點參數二叉樹；

圖4為實施例中所構建貝葉斯網t2節點參數二叉樹。

具體實施方式

本發明包括以下步驟：

步驟一，對可重構系統的故障-測試相關性關係進行建模。

和普通的單模式系統不同，可重構系統由於系統結構在使用過程中可能會依據環境的變化而變化。這意味著故障和測試之間的關係也是會變化的。此處，採用多模式多信號模型的方式進行表徵。該模型包含以下四種元素：故障、開關、測試點以及連接線，連接線用來連接故障、測試、及開關。該模型的含義為：如果故障和測試之間有連接通路，則故障和測試之間相關，否則不相關。其間可設置開關，通過開關的開啟和閉合可影響故障和測試之間的相關性關係，表示的含義為系統重構。

步驟二，對可重構系統相關性進行表徵

基於步驟一中所述的模型，對系統進行分析。得到一組共兩個相關性矩陣。假設系統共有m個故障模式，n個測試，k個開關。矩陣一為故障和測試之間的相關性關係，即d1＝[dij]m×n，其中dij∈{0,1}，取值為0表示第j個測試在任意模式下均無法檢測到第i個故障；取值為1表示第j個測試可以檢測到第i個故障。矩陣二為開關和測試之間的相關性，用d2＝[rij]n×k表示，其中rij∈{0,1}，取值為0表示第j個測試和故障的相關性不受第i個開關狀態的影響；取值為1表示第j個測試和故障的相關性和第i個開關的狀態相關。

步驟三，確定可重構系統貝葉斯網的結構

依據貝葉斯網的定義，貝葉斯網的結構包括節點以及節點之間的連接關係兩部分。本發明構建的可重構系統貝葉斯網由兩層共三類節點組成。第一層為故障和開關層，分別用故障節點和開關節點表示。第二層為測試層，用測試節點表示。故障節點和步驟二中所述的故障模式相對應，共有m個。開關節點和步驟二中所述的開關相對應，共有k個。測試節點和步驟二中的測試相對應，共有n個。

在確定好節點數目和類型後，為節點之間添加連接關係。添加的方式依據步驟二中兩個相關性矩陣進行。具體為：針對矩陣d1＝[dij]m×n，如果dij＝1則在第i個故障(用fi表示)和第j個測試(用tj表示)之間添加連接關係，方向由fi指向tj；針對矩陣d2＝[rij]n×k，如果rij＝1，則在第j個測試(用tj表示)和第i個開關(用si表示)之間添加連接關係，方向由si指向tj。

步驟四，確定可重構系統貝葉斯網的參數並採用樹形結構進行表徵

(1)針對故障節點，設置正常和異常兩種狀態，異常概率表示故障率。

(2)針對開關節點，設置開和關兩種狀態，概率分別設為0.5。

(3)針對某一個測試節點，用集合e＝{f,s}表示初始備選節點集，其中f表示與其相關的故障節點，s表示與其相關的開關節點。從集合e中選擇相關故障節點數目最多且不為0的開關節點作為下一步的樹節點。針對開關閉合分枝，從e中去除該開關節點；針對開關斷開這一分枝，從e中去除該開關節點以及和該開關相關的故障節點，更新e。若無開關節點，選擇故障率最高的故障節點作為下一步的樹節點，從e中去除該故障節點，更新e。針對故障存在這一分枝，存儲參數1，停止擴展該分枝；針對故障不存在這一分枝，若e中不包含其它故障節點，存儲參數0，否則，繼續選擇節點，擴展參數表達樹，直至達到停止條件。最終所得的二叉樹即為測試節點的參數。

實施例

步驟一，如圖1所示，為某可重構系統建立相關性模型。該系統包含f1,f2,f3三個故障模式，s1,s2兩個開關和t1,t2兩個測試。通過開關狀態的變化，可實現系統的重構。

步驟二，對所述可重構系統進行表徵。

在該系統中，m＝3，n＝2，k＝2。

步驟三，確定可重構系統貝葉斯網的結構

依據貝葉斯網結構確定規則，得到的貝葉斯網結構如圖2所示。

步驟四，確定可重構系統貝葉斯網的參數

(1)針對故障節點(即f1,f2,f3)，每一節點均有兩種狀態：故障和正常。故障的概率即故障率，假定三個故障率分別為0.1、0.3和0.6。

(2)針對開關節點(即s1,s2)，每一節點有兩種狀態：打開和關閉。兩者的發生概率均設為0.5。

(3)針對測試節點t1，初始備選節點為e＝{f1,f2,s1,s2}。和s1相關的故障節點數目為1，和s2相關的故障節點數目為2，為此選擇s2作為下一步的樹節點。針對開關閉合分枝，更新後的e』＝{f1,f2,s1}；針對開關打開分枝，e」＝{f1,s1}。然後依次類推，得出t1的參數表達樹如圖3所示。

針對測試節點t2，初始備選節點為e＝{f3}，其參數二叉樹如圖4所示。

以上顯示描述了本發明的基本原理和主要特徵和本發明的特點。本領域技術人員應該了解，本發明不受上述實施例的限制，上述實施例和說明書中描述的只是說明本發明的原理，在不脫離本發明精神和範圍的前提下，本發明還會有各種變化和改進，這些變化和改進都會落入要求保護的本發明範圍。本發明要求保護範圍由所附的權利要求書及其等效物界定。