一種構建帶約束最小二乘最大熵分位值函數模型的方法與流程

2023-04-24 23:00:46 2

技術領域：

本發明涉及航空結構件可靠性評估領域，具體涉及小樣本情況下航空結構件可靠性分析中的一種構建帶約束最小二乘最大熵分位值函數模型的方法。

背景技術：
：

基於航空結構件的外部激勵不僅與工況有關還受隨機因素影響、材料組織的不均勻性、內部缺陷等隨機分布及加工製造過程中尺寸公差分散性影響，航空結構件強度分析過程中可靠性分析是一個常見的問題：如結構疲勞設計中，求給定可靠度的疲勞壽命；結構剛度設計中，求給定可靠度的結構位移響應等。

目前解決可靠性問題一般採用傳統概率統計方法，即概率分布假設、驗證及分布參數估計，但存在如下問題：(1)計算過程麻煩、效率低；(2)由於概率分布假設、驗證環節容易引入人為誤差，使估算的概率分布與實際分布存在誤差；(3)只能處理單峰隨機變量，無法應用於複雜隨機變量中(如多峰)。

最大熵原理是近代發展的一種處理概率統計的有力工具。應用最大熵原理擬合分位值函數公式時具有不事先假定概率分布、最小化人為幹擾因素、公式統一、適用性強等優點且在擬合複雜概率分布時能夠克服常見概率分布模型無法應用的缺點。在大樣本情況下(樣本數大於100件)，最大熵分位值函數模型能精確地估算樣本分位值函數；但工程上特別是航空產品試驗次數較少(一般低於10件)，此時最大熵分位值函數模型估算精度較差。本文中將最大熵分位值函數模型稱為經典型最大熵分位值函數模型。

技術實現要素：
：

發明目的：針對小樣本情況下傳統概率統計方法計算效率不高及經典型最大熵分位值函數模型計算精度差的情況，本發明提出一種構建帶約束最小二乘最大熵分位值函數模型的方法，以提高小本樣情況下分位值函數的計算效率及估算精度。

本發明採用如下技術方案：

一種構建帶約束最小二乘最大熵分位值函數模型的方法，該方法包括以下步驟：

(1)建立任意一隨機變量x的無約束最小二乘最大熵分位值函數模型：

x(u)為隨機變量x的無約束最小二乘最大熵分位值函數值；u(x)為x的累積分布函數值，u(x)＝p(x≤x)且滿足0≤u(x)≤1；λls-qf，j為拉格朗日乘子，即待定係數，j＝0，1，...，m，拉格朗日乘子個數為m+1；

(2)選取隨機變量x的一組樣本點作為中位秩點，並計算各中位秩點的經驗累積分布函數值，定義為中位秩點xi的經驗累積分布函數值，x1≤x2≤xi…≤xn，n為樣本個數；用無約束最小二乘最大熵分位值函數模型擬合中位秩點，並且保證擬合後的無約束最小二乘最大熵分位值函數曲線上每個點關於分位值的斜率大於0，得到無約束最小二乘最大熵分位值函數曲線x(u)slope＞0，下標slope＞0表示x(u)的導數大於0；

(3)定義無約束最小二乘最大熵分位值函數曲線x(u)slope＞0上的點以(累積分布函數值，分位值函數值)形式表示，選取x(u)slope＞0的中段曲線點形成點集c1，c1＝(ur，x(ur)slope＞0)，r＝1，...，m，其中ur為從曲線x(u)slope＞0上均勻選取的累積分布函數值，ur∈[umin，umax]，[umin，umax]為預設的閾值區間；m為選取的累積分布函數值的總數；

(4)應用威布爾分布模型擬合步驟(2)選出的樣本，得到威布爾分位值函數曲線x(u)weibull；選取威布爾分位值函數曲線兩側尾部曲線點形成點集c2和c3：

其中，us為從曲線x(u)weibull均勻選取的累積分布函數值，s＝1，...，m；

(5)由點集c1，c2，c3構成大的點集c，即c＝c1∪c2∪c3；用無約束最小二乘最大熵分位值函數模型擬合點集c，得到帶約束最小二乘最大熵分位值函數曲線。

進一步的，所述採用無約束最小二乘最大熵分位值函數模型擬合任意一組樣本的步驟為：

(2-1)定義待擬合的樣本為d1，d2，…，dp，dp的累積分布函數值為up，p＝1，2，…，p；

(2-2)構建優化函數式中：

(2-3)通過最小二乘法求解minq，得到拉格朗日乘子

(2-4)將求出的拉格朗日乘子代入無約束最小二乘最大熵分位值函數模型，便可確定對應樣本的最小二乘最大熵分位值函數。

進一步的，所述中位秩點xi的經驗累積分布函數值計算公式為：

進一步的，umin＝0.001，umax＝0.999。

本發明具有如下有益效果：

本發明能夠成功地應用於小樣本情況下航空結構件可靠性分析分位值函數估計問題，相比傳統概率統計方法，本發明計算效率高、能處理複雜隨機變量；相比經典型最大熵分位值函數模型，本發明計算精度高且穩定。

附圖說明：

圖1為服從正態分布的8個隨機樣本分別由威布爾分布模型、無約束最小二乘最大熵分位值函數模型與帶約束最小二乘最大熵分位值函數模型擬合得到的分位值函數曲線計算精度對比圖；

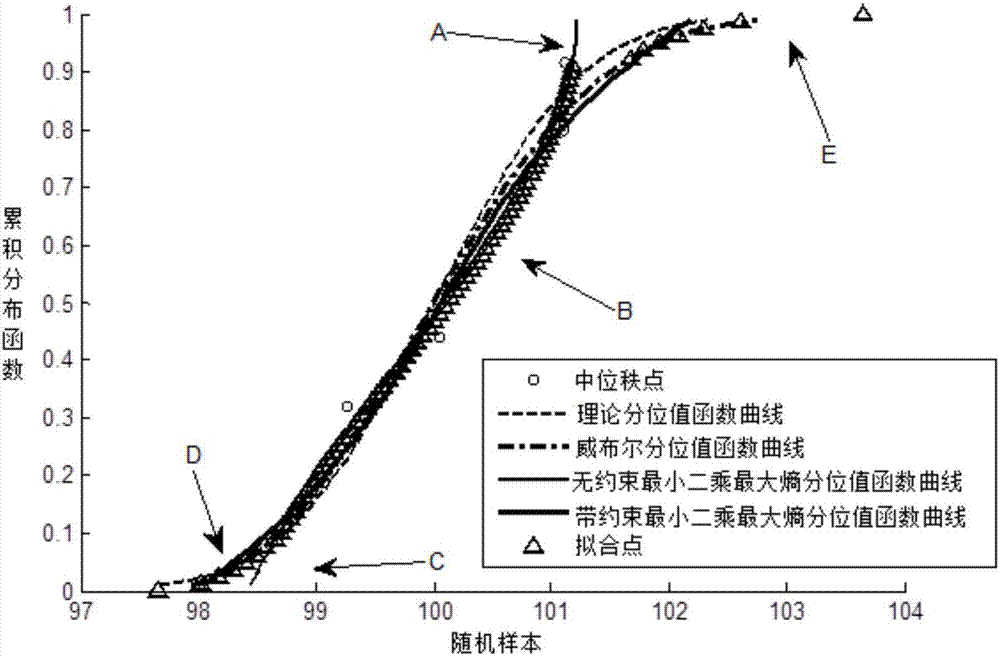
圖2為基於帶約束最小二乘最大熵分位值函數模型的分位值函數曲線擬合過程圖；

圖3為服從正態分布的8個隨機樣本分別由經典型最小二乘最大熵分位值函數模型與帶約束最小二乘最大熵分位值函數模型擬合得到的分位值函數曲線計算精度對比。

具體實施方式：

下面結合附圖和實施例對本發明進一步說明。

圖2所示為基於帶約束最小二乘最大熵分位值函數模型的分位值函數曲線擬合過程圖，如下步驟：

1)建立無約束最小二乘最大熵分位值函數模型

設隨機變量x，u(x)＝p(x≤x)為x的累積分布函數值，且滿足0≤u(x)≤1，則隨機變量的無約束最小二乘最大熵分位值函數x(u)為：

式中，λls-qf，j(j＝0，1，...，m)為拉格朗日乘子，也就是待定係數；拉格朗日乘子個數為m+1。累積分布函數u(x)與無約束最小二乘最大熵分位值函數x(u)互為反函數。

拉格朗日乘子的確定步驟如下：

11)重新推導式(1)得：

由數值仿真得到隨機變量x的一組服從某一概率分布的隨機樣本點或真實實驗數據，本例中隨機樣本點服從正態分布，設這一組隨機樣本點為：x1，x2，...，xn且x1≤x2≤…≤xn。

12)定義ui是xi的累積分布函數值，其中xi是隨機變量x的第i個次序統計量，i∈[1，2，…，n]；ui由適當的中位秩法來獲得：

13)通過最小二乘法求解優化函數minq，得到拉格朗日乘子

式中：

將求出的拉格朗日乘子代入公式(1)，便可確定隨機變量x的無約束最小二乘最大熵分位值函數(lsmeqfm)。但在某些情況下，無約束最小二乘最大熵分位值函數不是累積分布函數值的單調函數且分位值函數曲線尾部誤差較大，故計算拉格朗日乘子時引入約束條件，進一步提出帶約束最小二乘最大熵分位值函數模型(lsmeqfmcc)。

2)建立帶約束最小二乘最大熵分位值函數模型，步驟為：

21)以(x1，x2，...，xn)為中位秩點，計算樣本的經驗累積分布函數值其中：

22)計算無約束最小二乘最大熵分位值函數x(u)關於累積分布函數值u的導數x′(u)為：

若要滿足無約束最小二乘最大熵分位值函數x(u)是積累分布函數值u的單調函數，則需要滿足x′(u)＞0。當x′(u)＞0時，因為大於0，所以大於0。即需要在無約束最小二乘最大熵分值函數模型的基礎上增加約束條件：

其中，r為uk在區間[uminumax]均勻取值的個數。

應用無約束最小二乘最大熵分值函數模型擬合樣本(x1，x2，...，xn)，並且保證擬合後的無約束最小二乘最大熵分位值函數曲線上每個點關於分位值的斜率大於0，得到無約束最小二乘最大熵分位值函數曲線x(u)slope＞0。

23)定義無約束最小二乘最大熵分位值函數曲線x(u)slope＞0上的點以(累積分布函數值，分位值函數值)形式表示，選取x(u)slope＞0的中段曲線點形成點集c1，c1＝(ur，x(ur)slope＞0)，r＝1，...，m，其中ur為從曲線x(u)slope＞0上均勻選取的累積分布函數值，ur∈[umin，umax]，[umin，umax]為預設的閾值區間；m為選取的累積分布函數值的總數；

24)基於威布爾分布曲線尾部具有很好擬合性質，應用威布爾分布模型擬合樣本(x1，x2，...，xn)，得到威布爾分位值函數曲線x(u)weibull；選取威布爾分位值函數曲線兩側尾部曲線點形成點集c2和c3：

其中，us為從曲線x(u)weibull均勻選取的累積分布函數值，s＝1，...，m；m為選取的累積分布函數值的總數。

25)由點集c1，c2，c3構成大的點集合c，應用無約束最小二乘最大熵分位值函數模型擬合點集合c得到帶約束最小二乘最大熵分位值函數曲線。

下面通過具體實施例對本發明技術方案做進一步說明。

圖1為服從正態分布的8個隨機樣本分別由威布爾分布模型、無約束最小二乘最大熵分位值函數模型與帶約束最小二乘最大熵分位值函數模型擬合得到的分位值函數曲線計算精度對比圖；帶約束最小二乘最大熵分位值函數模型計算精度較高，克服無約束最小二乘最大熵分位值函數模型擬合分位值函數時，曲線尾部a和c處計算精度較差的情況。

s1：設選出的8個隨機樣本為x1，x2，...，x8，且滿足x1≤x2≤…≤x8，計算各樣本點的經驗累積分布函數值，即

稱隨機樣本點為中位秩點，x1，x2，...，x8所對應的分位值和累積分布函數值的具體數據如表1所示：

表1中位秩點數據

s2：應用無約束最小二乘最大熵分位值函數模型擬合中位秩點x1，x2，...，x8，並且保證曲線上每個點關於分位值的斜率大於0，得到無約束最小二乘最大熵分位值函數曲線，如圖2所示。由圖2可知，無約束最小二乘最大熵分位值函數曲線尾部的計算誤差較大，如a、c兩處。

s3：令m＝1000，[umin，umax]為[0.001，0.999]，設分位值函數曲線上的點由(累積分布函數值，分位值函數值)表示，選取無約束最小二乘最大熵分位值函數曲線的中段曲線點，見圖2中的b處，並設為點集c1＝(ur，x(ur)slope＞0)，其中ur∈[0.001，0.999]，和的取值可根據實際情況確定，本例中

s4：應用三參數威布爾分布模型擬合隨機樣本(x1，x2，...，x8)，得到威布爾分位值函數曲線x(u)weibull，如圖2所示。從圖2中可以看出威布爾分位值函數曲線與理論分位值函數曲線在尾部較為吻合，說明威布爾分布函數具有較好的尾部擬合特性。

選取威布爾分位值函數兩側尾部曲線點，見圖2中的d處和e處，設為點集c2和c3：

c2＝(us，x(us)weibull)，0.001≤us≤0.1；

c3＝(us，x(us)weibull)，0.9≤us≤0.999；

其中us(s＝1，...，1000)為從區間[0.001，0.999]中均勻選取的累積分布函數值。

s5：由點集c1，c2，c3構成大的點集合c，即c＝c1∪c2∪c3。應用無約束最小二乘最大熵分位值函數模型擬合點集合c得到帶約束最小二乘最大熵分位值函數曲線，如圖1所示。可以看出帶約束最小二乘最大熵分位值函數曲線與理論分位值函數曲線吻合較好，且在曲線尾部計算精度較無約束最小二乘最大熵分位值函數曲線高。

上述技術方案中，採用無約束最小二乘最大熵分位值函數模型擬合任意一組樣本的步驟如下：

a)定義待擬合的樣本為d1，d2，…，dp，dp的累積分布函數值為up，p＝1，2，…，p；

b)構建優化函數式中：

c)通過最小二乘法求解minq，得到拉格朗日乘子

d)將求出的拉格朗日乘了代入無約束最小二乘最大熵分位值函數模型，便可確定對應樣本的最小二乘最大熵分位值函數。

圖1、圖3所示為針對小樣本情況下隨機變量的不同最大熵分位值函數模型計算精度對比，可以看出帶約束最小二乘最大熵分位值函數模型計算精度最高。各最大熵分位值函數模型計算精度具體數據如表2所示：

表2不同最大熵分位值函數模型計算精度對比

表2中rmse表示均方根誤差：

其中，為隨機樣本值xi的估計值。

以上所述僅是本發明的優選實施方式，應當指出，對於本技術領域的普通技術人員來說，在不脫離本發明原理的前提下，還可以做出若干改進和潤飾，這些改進和潤飾也應視為本發明的保護範圍。