非線性切換雙時標系統滑膜控制方法與流程
2023-10-18 00:51:29
本發明屬於複雜系統控制技術領域,特別是提供了一種非線性切換雙時標系統滑膜控制方法,適用於板帶軋制、機器人柔性臂、醫療機械臂以及複雜電路等複雜系統的建模與高精度控制。
背景技術:
非線性切換雙時標系統控制問題是一類涉及切換和時標變換兩種問題的複雜系統控制難題,廣泛存在於板帶軋制、智慧機器人以及電力電子等領域。因該類問題,目前普遍採用的經典控制理論與方法已無法滿足日益增長的控制精度需求,迫切需要提出新理論與方法。
近年來針對非線性系統、切換系統以及雙時標系統的研究得到較大進展,但考慮非線性、切換性和雙時標性並存情形的複雜系統建模與控制問題尚處於初步階段,因為上述三種特性的存在將大大加大系統控制器設計難度,需多種學科的融合與交叉研究。奇異攝動技術是處理雙時標問題的有效工具,但當系統中還存在切換特性時,解決小攝動參數引起的數值病態問題是切換雙時標系統控制器設計問題的難點。
滑膜控制方法是一種通過設計切換規則,使子系統之間自由轉換運行,從而實現整個閉環控制系統漸進穩定的控制方法,自20世紀50年代由蘇聯學者Emelyanov提出後,獲得廣泛研究,但將其應用於雙時標系統的研究尚未發現。綜上所述,研究切換雙時標系統的建模與滑膜控制問題,對此類系統的高精度控制具有較大貢獻,具有重要的理論意義和實際應用價值。
本發明在國家自然科學基金面上項目(51374082)的資助下提出了非線性切換雙時標系統的離散模糊奇異攝動建模與滑膜控制方法。
技術實現要素:
本發明的目的在於提供一種非線性切換雙時標系統滑膜控制方法,是一種非線性切換雙時標系統的離散模糊奇異攝動建模與滑膜控制方法,解決現有控制方法在處理被控對象子系統間的無障礙切換和極大減少快時標引起的穩態誤差上的問題。
本發明的技術方案是:一種離散模糊奇異攝動切換模型構建與滑膜控制方法,該方法建立離散奇異攝動切換模型,描述被控切換雙時標系統的動力學特性,然後設計高精度滑膜控制器。上述方法應用於實際系統時所採用的整體硬體結構與常規控制系統方法相同,主要包括:被控對象,傳感器,控制器,通訊部件以及執行器。
步驟1、根據被控對象的動力學方程,建立其離散模糊奇異攝動切換模型。
將被控系統的小參數相關或變化較快的狀態變量看作為快變量,變化相對緩慢或可測狀態變量看作為慢變量,建立具有多個子系統的離散模糊奇異攝動切換模型。
規則i:如果ξ1(k)是φi1,…,ξg(k)是φig,那麼
x(k+1)=EεAiσ(k)x(k)+EεBiσ(k)u(k) (1)
其中,
xs(k)∈Rn為慢變量,xf(k)∈Rm為快變量,u(k)∈Rq為控制輸入,φi1,...,φig(i=1,2,...,r)均為模糊集合,ξ1(k),...,ξg(k)為可測量的系統變量,Aiσ(k),Biσ(k)為適當維數矩陣,切換信號σ(k):[0,+∞)→{1,2,…,N},σ(k)=j表示在k時刻切換系統的第j個子系統被激活,N為子系統個數,ε為奇異攝動參數,In×n,Im×m分別為n階單位陣和m階單位陣。
給定[x(k);u(k)],利用標準模糊推理可得全局模糊模型為
x(k+1)=Eε[Aσ(k)(μ)x(k)+Bσ(k)(μ)u(k)] (2)
其中,
隸屬度函數φij(ξj(k))為ξj(k)在φij中的隸屬度,設wi(ξ(k))≥0,i=1,2,…,r,r為規則數,μi(ξ(k))≥0,為了便於記錄我們令μi=μi(ξ(k))。
步驟2、設計滑膜控制器
假設系統狀態完全可測,構造如下滑模函數:
其中,Gσ(k)∈R(n+m)×q為控制器參數矩陣且使
Aσ(k)(μ)-Bσ(k)(μ)[Hσ(k)(μ)Bσ(k)(μ)]-1[Hσ(k)(μ)Aσ(k)(μ)+Gσ(k)] (5)
為Hurwitz的。
考慮如下滑模函數差:
根據滑模控制理論可知,當系統狀態到達滑模面時,有S(k+1)-S(k)=0,因此,可得等價控制律
將控制律(7)帶入式(2),得到如下滑動模態方程:
步驟3、求解控制器增益。
融合切換控制理論、Lyapunov穩定性定理、線性矩陣不等式方法,推導出如定理1所示的滑膜控制器存在條件。
定理1:對於充分小的攝動參數ε>0,控制率(7)使得切換雙時標系統(2)漸進穩定,若且唯若存在矩陣Gσ(k)∈R(n+m)×q使式(9)為Hurwitz的,正定對稱矩陣Pσ(k)使線性矩陣不等式(10)成立。
Aσ(k)(μ)-Bσ(k)(μ)[Hσ(k)(μ)Bσ(k)(μ)]-1[Hσ(k)(μ)Aσ(k)(μ)+Gσ(k)] (9)
其中,i=1,2,…,r,q為控制輸入的維數,切換信號
切換區域βj為
βj={x(k)|xT(k)Pj x(k)≥0},j=1,2,…,N (12)
N為被控系統的切換子系統個數。
步驟4、將上述切換模型與控制律描述為C語言代碼,植入控制器,實現被控系統高精度控制。
本發明的優點:
1)、融合模糊邏輯、切換系統和奇異攝動理論,提出模糊奇異攝動切換模型構建方法,解決了現有建模理論無法準確描述非線性切換雙時標系統的動力學與運動學特性問題,為非線性切換雙時標系統的建模提供新思路。
2)、結合滑膜理論與模糊控制方法,提出基於模糊奇異攝動切換模型的滑膜控制方法,解決了現存控制技術難以消除被控系統切換特性和快變量引發的穩態誤差難題,為非線性切換雙時標系統的高精度控制提供新方法。
附圖說明
圖1本發明方法的流程圖。
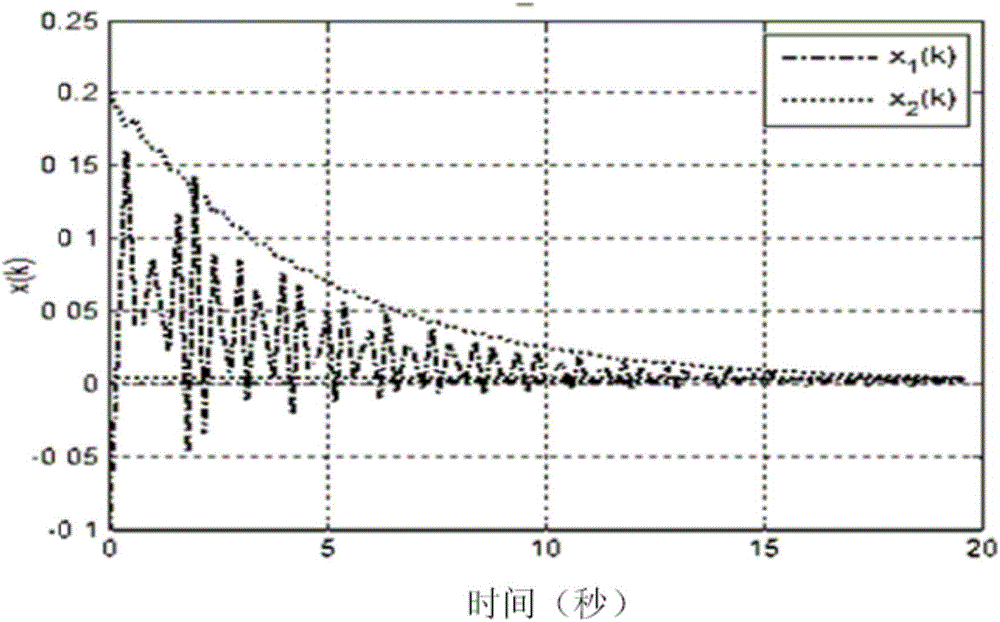
圖2閉環系統狀態響應曲線圖。
圖3滑模函數響應曲線圖。
圖4切換信號圖。
具體實施方法
下面將本發明方法應用於如下具有兩個模態的切換系統,說明其實施方法。
步驟1、針對一種具有兩個模態的切換系統,建立如下離散模糊奇異攝動切換模型。
規則i:如果ξ1(t)是φi1,那麼
x(k+1)=EεAiσ(k)x(k)+EεBiσ(k)u(k) (13)
其中,
xs(k)∈R為慢變量,xf(k)∈R為快變量,u(k)∈Rq為控制輸入,ξ1(k)=xs(t),φi1為模糊集合,i=1,2,ε=0.01,
當σ(k)=1時對應子系統1的系統參數為:
當σ(k)=2時對應子系統2的系統參數為:
給定[x(k);u(k)],利用標準模糊推理可得全局模糊模型為
x(k+1)=Eε[Aσ(k)(μ)x(k)+Bσ(k)(μ)u(k)] (14)
其中,
μ2(xs(k))=1-μ1(xs(k)) (17)
假設系統的初始狀態為x(0)=[-0.1 0.2]T,
其中,
滑模控制器為
其中,σ(k)=1,2,
仿真結果(如圖1-圖4)表明,本發明方法不僅能使被控非線性切換雙時標系統各子系統間的自由切換而且還能降低快變模態引起的穩態誤差,從而達到其高精度控制目標。
