一種晶片電子封裝結構的精確電磁分析方法與流程

2023-10-06 03:27:59 2

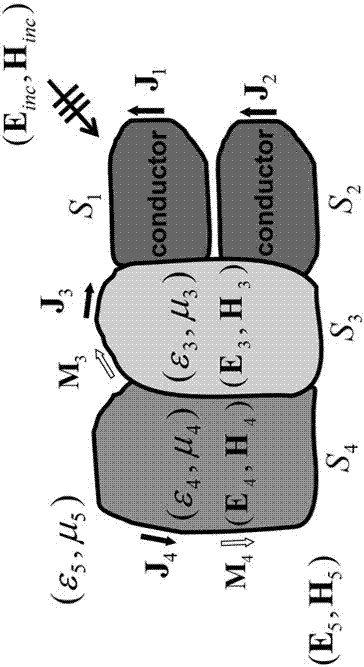
本發明涉及晶片電子封裝中電磁場矩量法分析領域，具體涉及應用於晶片封裝中電磁兼容設計的分析方法。

背景技術：
隨著電子產品晶片複雜度的不斷提高，噪聲容限、功耗和特徵尺寸不斷降低，同時，隨著互聯線所傳輸的脈衝信號擴展到微波、毫米波頻段。互連線已不能簡單視為無電阻、無電容、無電感的金屬導線。在高頻或交流的情況下，信號的波長與封裝引線的尺寸處於同一數量級，信號脈衝在互連線上呈現明顯的波動效應。因此，在現代高速大規模集成電路系統中，對互聯、封裝結構尤其是互連線系統電磁特性的分析在整個高速集成電路系統的分析和設計中佔有越來越重要的地位。當封裝結構中包含介質材料時，已有的選擇是RWG基函數或RWG基函數來表達磁流。如果選擇RWG基函數，則電流和磁流均使用RWG基函數來表達。在這種情況下，用矩量法求解電場積分方程和磁場積分方程時所得到的結果系統矩陣將會是病態的。考慮單個介質物體的電磁散射情況，電場積分方程可以表示為：引入算符,,定義如下：其中A表示J或者M,是並矢格林函數(為單位並矢，為三維標量格林函數)；通常試函數也被選為RGW基函數，這時算符將在上述兩個電場積分方程中都不能夠被有效地測試，因為在運算符的對磁流有的操作，這一主項在測試後會消失，從而產生病態的系統矩陣。因此，有人選用RWG基函數作為第一個積分方程的試函數，而選擇RWG基函數作為第二個積分方程的基函數，也就是在擴展函數不能夠正交的情況下選擇一對相互正交的基函數，使系統矩陣能夠是良態的。但是使用RWG基函數作為試函數時，我們不能夠將算符中的並矢格林函數的一個梯度運算符移動到測試函數上，由此我們必須處理算符中的的強奇異性。儘管有關的技術已經能夠處理這樣的強奇異性，但是在實施過程中會產生很大的不方便。

技術實現要素：
考慮到使用RWG基函數同時表示電流和磁流的缺點，有人提出用RWG基函數表示電流而用RWG基函數表示磁流。這種情況下，儘管系統矩陣通常會是良態的，但是數值解會不精確。這是因為RWG基函數在三角形之間不是連續的，並且當對磁流求散度時會在三角形的邊界會產生虛擬的線電荷。由於RWG基函數和RWG基函數都不能理想的表示磁流，本發明提出採用對偶基函數來解決這個問題。對偶基函數與RWG基函數有著相同特性，但是與RWG基函數在空間中幾乎正交。如果將它們共同使用，磁流和電流都能夠被合適的表示，並且系統矩陣性態也比較好。為此，本發明給出的技術方案為：一種晶片電子封裝結構的精確電磁分析方法，其特徵在於，應用於晶片電子封裝的電磁場矩量法分析，通過使用對偶基函數和RWG基函數分別來表示磁流和電流，從而達到比僅使用RWG基函數或者RWG基函數更加優良的分析結果，減弱了晶片尺寸遠小於電磁波波長所帶來的負面影響，並且本發明方法對於矩量法中網格的分割沒有苛刻的要求，使得運用更為廣泛，結果更加精確。上述本發明提出的互聯和封裝結構高效電磁分析的新方法，該方法使用對偶基函數來表示磁流，極大提高了計算精度，並且在低頻和較差網格質量的情況下結果依然很好，因此具有一定的實際應用價值。與現有技術相比，本發明技術方案帶來的有益效果：典型的互聯和封裝結構通常要求頻率低於1GHz，在這種情況下，結構的尺寸相對于波長很小。在低頻的情況下系統矩陣可能是病態的，即使可以解決，其數值解也不精確。Loop-tree和loop-star基函數是可以解決低頻問題的有效工具，但是由於實施上的難度在封裝問題中沒有被廣泛採用。並且封裝分析需要包含很寬的頻域，但是loop-tree和loop-star基函數隻適用於中頻和高頻。相對於這幾種基函數，對偶基函數在低頻下...