一種基於轉速的缸壓曲線重構方法與流程
2023-06-03 04:30:01 2
本發明屬於氣缸數據分析處理領域,尤其涉及一種基於轉速的缸壓曲線重構方法。
背景技術:
氣缸廣泛應用於各生產操作及機械設備中,一旦其發生故障,將可能導致設備停機,影響正常生產工作秩序甚至造成安全事故,因此,為保證氣缸安全穩定工作,需要在氣缸早期設計以及後期使用過程中對氣缸各項指標數據進行分析判斷,以使氣缸獲取和保持最佳的使用狀態。其中缸壓重構是反映氣缸壓力變化情況,表現實際工作狀態的重要數據,經常應用於氣缸的生產檢測,設計優化等工作過程中。由於氣缸工作過程中缸內氣壓大、溫度高、變化快因此不容易測量,特別是對一些不可拆卸或者正在使用中的氣缸進行測量時,無法直接獲取氣缸內部的數據。
技術實現要素:
本發明的目的在於,提供一種基於轉速的缸壓曲線重構方法,其步驟少,數據採集及處理簡單,能夠重構缸壓數據。
為實現上述目的,本發明創造採用如下技術方案。
一種基於轉速的缸壓曲線重構方法,其特徵在於,包含以下步驟:
利用傳感器獲取模擬信號,包括氣缸中齒輪或飛輪的轉速脈衝信號,齒輪旋轉的角位移脈衝信號,以及氣缸上止點脈衝信號;
將上述轉速脈衝信號、角位移脈衝信號及氣缸上止點脈衝信號分別使用比較器處理,將上述模擬信號(即不規則方波信號)轉換為規則方波信號;
以上述模擬信號轉換的數位訊號為基礎數據,尋找數位訊號中的上升沿數據點位置,通過兩個上升沿之間的數據總數以及採樣頻率確定瞬時轉速得到瞬時轉速的數位訊號數據;
對上述瞬時轉速信號數據形成的曲線圖進行emd經驗模態分析後得到imf分量曲線圖及數據,選取與發動機頻率相同或相近的曲線圖進行疊加,得到真是瞬時轉速曲線圖及數據;再使用巴特沃斯貸通平滑濾波器進行處理;
將上述經處理形成的平滑的真實瞬時轉速數據代入以下公式進行計算得到缸壓重構數據以及曲線圖;
其中
m1:往復運動集中換算質量;
j:旋轉運動集中轉動慣量;
r:曲軸半徑;
第k缸相對第一缸的發火相位;
角速度;
角加速度;
f函數為:f(x)=(sin(x)+(r/l)*sin(2x)./(2*sqrt(1-(r/l)2*sin(x).^2))g函數為:g(x)=cos(x)+(r/l)*cos(2x)./sqrt(1-(r/l)2*sin(x).^2)+((r/l)3*sin(2x).^2)/(4*sqrt(1-(r/l)2*sin(x).^2).^3)
較優地,所述巴特沃斯貸通平滑濾波器用振幅的平方對頻率的公式可表示為:
其中,n=濾波器階數;
ωs=截止頻率=振幅下降為-3分貝時的頻率;
ωp=通頻帶邊緣頻率;
在通頻帶邊緣的數值為:
其有益效果在於:
本發明創造的一種基於轉速的缸壓曲線重構方法,其通過可以經外部快速測量獲取的瞬時轉速、角位移、上止點信號等數據,利用自編函數及比較器快速計算重構缸壓數據,本方法需要測量的數據少,所需設備簡單,採集效率高,後期處理計算量少,對計算系統性能要求低,缸壓重構結果好。
附圖說明
圖1是本發明創造的具體實施步驟圖;
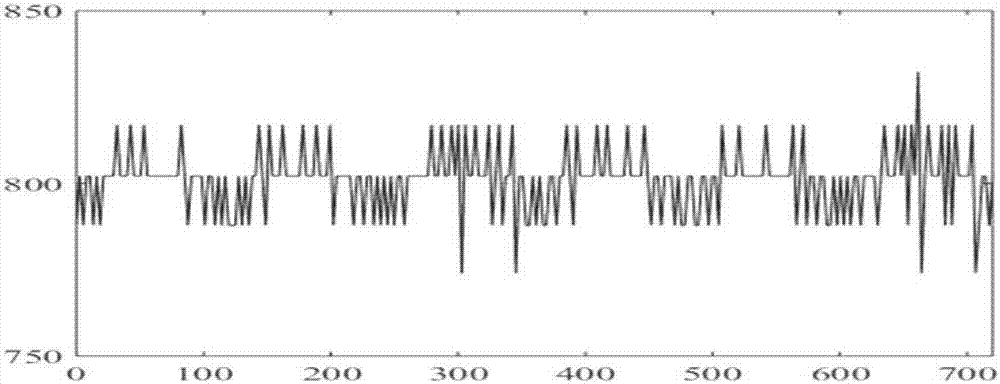
圖2是實施例中對採集的數據經過處理後獲得的未處理的循環轉速圖;
圖3是由循環轉速圖經處理後獲得的imf分量轉角域值以及圖像;
圖4和圖5是imf分量的頻譜和瞬時頻率圖;
圖6是由各imf分量波形圖經過疊加形成的真實瞬時轉速曲線圖;
圖7是經過巴特沃斯貸通濾波器平滑處理後的轉速圖像;
圖8是對實施例中具體柴油機進行處理的計算模型;
圖9是實施例中對具體柴油機進行缸壓重構獲得的曲線。
具體實施方式
以下結合具體實施例對本發明創造作詳細說明。
本發明創造的基於轉速的缸壓曲線重構方法,其實施過程如圖1所示,其具體實施步驟包括:
1、信號採集方法;
本發明的一種基於轉速的缸壓曲線重構方法的基礎數據包括轉速脈衝信號,角位移脈衝信號,氣缸上止點脈衝信號。
實際應用中,由於氣缸內各齒輪的齒數及直徑都已經確定,其轉速u可以相互轉換,因此可以採用可以採用測量氣缸內任意齒輪的轉速u來進行計算,為便於操作及觀察,優選測量汽缸外的飛輪的轉速u進行計算。本實施例中利用傳感器測量飛輪的轉速u,利用編碼器採集飛輪角位移信號,通過在氣缸的上止點位置設置傳感器以收集上止點信號。
較優地,上述傳感器可以採用磁電傳感器。利用數據採集器,如ni9222等,可便捷的採集多路信號,滿足測量需要。
在進行信號採集的過程中,根據需要設置採集頻率f0為4-10倍齒輪信號頻率f1,由齒輪的平均轉速ω1可估算齒輪信號頻率f1=ω1(實驗值ω1=800),即f0=kf1=kω1,k∈[4.10];
信號採集周期的長短決定了總得信號點個數以及信號精度;根據實際需要,採集5-10s可保證達到需要的計算精度。
2、模擬信號的數位化處理
使用matlab軟體對收集到的信號進行後序處理,
a、對齒輪脈衝信號new的處理,根據傳感器輸出的信號波形的極值點數值範圍[m,n],(a<b),規定大於x的信號(a<x<b)為x1(x1>0),小於x的信號為0;
b、對編碼器脈衝信號bmq的處理,根據編碼器輸出的信號波形的極值點數值範圍[s,t],(s<t),規定大於r的信號(s<r<t)為r1(r1>0),小於r的信號為0;
c、將上述處理後的信號作為基礎文件利用比較器進行對比,尋找上升沿,以確定齒輪位置,所述比較器內容如下,
為便於後文描述,定義x=5,x1=10,r=2.5,r1=5;
利用比通過自編比較器使不規則方波變為規則方波,無需計算過零點,減少了計算量,
提高了測量以及計算效率。
3、計算瞬時轉速;
首先尋找斜率為x1=10的點,即上升沿對應點,每兩個上升沿代表齒輪旋轉一周,根據採樣頻率以及兩個上升沿之間的間隔點數計算瞬時轉速,計算公式為其中v為瞬時轉速,f0為採樣頻率,ds+1-ds為兩個上升沿之間採樣點數,n為飛輪齒數(後文中以試驗中齒輪齒數n=136為基礎進行計算)。其計算公式在計算機中表達為,
......
a=find(diff(new)==10);%斜率為10的點的位置
fori=1:length(a)-1;
v(i)=60*f0/(a(i+1)-a(i))/136
end
v=[v,v(end)]
szd=szd(a);%齒輪上止點位置
szd1=find(szd(1:200)==szd(1:200)));%尋找第一個上止點
n=v(szd1:szd1+271);
save(』循環轉速未處理.mat』,』n』)
......
通過需尋找斜率為定值的脈衝點,結合齒數等相關數據,確定齒輪瞬時轉速數據,不需要對齒輪進行逐點計算取值,減少了計算量,簡化數據處理過程。
利用matlab軟體及上述經過上述公示處理後得到未處理的循環轉速如圖2中所示;
matlab軟體對pc性能要求低,降低本方法測量的成本,擴大其應用場合。
4、獲取真實瞬時轉速曲線圖;
在上述未處理的循環轉速圖的基礎上,運用emd經驗模態分析方法對圖形進行處理,獲得各imf分量轉角域值以及圖像,如圖3中所示。
其中用於進行emd經驗模態分析的emd函數及步驟如下,
......
load(』循環轉速未處理.mat』)
z=n;
figure(1)
t=linspace(0,720,272);
set(gcf,』color』,』w』)
plot(t,z,』k』)
set(gca,』fontname』,’timesnewroman』)
set(gca,』fontsize』,14.0)
axis([0720750850])
c=emd(z)
......
5、對得到的imf數據進行希爾伯特黃變換(hht變換):
利用hhmspectrum_new、disp_hhms_new、hhspectrum、hhspectrum1函數對各imf分量進行變換處理,其中fliplr為矩陣翻轉函數,得到imf分量的頻譜和瞬時頻率圖,如圖4、圖5中所示。
其中,用於進行hht變換的計算函數如下,
......
%估算個分量的瞬時頻率及作圖
defspl=270;
[a,f,tt]=hhspectrum(c);
psd=hhmsdisphhms
pectrum_new(a,f,270);
disp_hhms_new(psd,defspl);
li=length((c(;,1)));
%各分量的功率譜
6、獲取真實瞬時轉速曲線圖;
在上一部的基礎上,根據發動機頻率比較並選擇1倍頻以下的波形做疊加得到真實瞬時轉速曲線圖,如圖6所示。
利用巴特沃斯貸通濾波器對上述真實瞬時轉速曲線圖進行平滑處理,巴特沃斯貸通濾波器可用如下振幅的平方對頻率的公式表示
其中,n=濾波器階數
ωs=截止頻率=振幅下降為-3分貝時的頻率
ωp=通頻帶邊緣頻率
在通頻帶邊緣的數值為:
得到平滑的瞬時轉速和轉速曲線。所得轉速圖形如圖7
7、缸壓重構;
將瞬時轉速單位r/pm轉換為角速度單位rad/s;
在進行缸壓重構過程中,本實施例採用柴油機非線性動力學模型,將摩擦力矩等阻力矩視為定值進行計算,計算模型如圖8所示。
輸入柴油機的結構參數(以下數據為實驗用設備的數值):
往復運動集換算質量/kg,m1=20;旋轉運動換算質量/kg,m2=1000;
曲軸半徑/m,r=0.065;連杆長度/m,l=0.219;有效輸出功率,ne=30;
機械效率,eta=0.88;曲軸連杆比,lam=r/l;
根據下方公式重構壓力曲線。
式中:
m1:往復運動集中換算質量;
j:旋轉運動集中轉動慣量;
r:曲軸半徑;
第k缸相對第一缸的發火相位;
角速度;
角加速度;
f函數定位及表達為:
......
functionf_phi=f(phi)
r=0.065;
l=0.219;
lam=r/l
f_phi=sin(phi)+lam*sin(2*phi)./(2*sqrt(1-lam2*sin(phi).2))
......
f函數定位及表達為:
functiong_phi=g(phi)
r=0.065;
l=0.219;
lam=r/l
g_phi=cos(phi)+lam*cos(2*phi)./sqrt(1-lam2*sin(phi).2)+lam3*sin(2*phi).2/(4*sqrt(1-lam2*sin(phi).2).3)
最後得到的壓力曲線圖如圖9所示。
需要指出的是,本具體實施例的計算過程中主要是在matlab數學軟體中進行,因此其函數及方法均使用相應的資料庫及函數形式,運用本方法或思路也可以利用其他數學軟體或分析軟體以不同形式或函數再現,本實施例僅為具體表達計算方法和思路,不應當理解為對本發明創造的限制。
