一種基於PLS‑SVM的通用單相諧波負荷建模方法與流程
2023-12-03 13:01:56 2
本發明涉及節能與電工儀器儀表領域,並且更具體地,涉及一種基於偏最小二乘法-支持向量機PLS-SVM的通用單相諧波負荷建模方法。
背景技術:
隨著電力電子裝置以及非線性負荷電氣設備的大量使用,造成了日益嚴重的諧波汙染問題。精確的元件模型是電力系統諧波精確分析的基礎,同步電機、變壓器和輸電線路的諧波建模工作已取得了很大的進展,如基於有限元的永磁同步電機一般化d-q軸模型建模方法以及變壓器有源諧波模型等。相對而言,負荷的諧波建模研究還很不成熟。在目前的電力系統仿真計算中,使用的負荷模型比較簡單,僅僅是單一結構的負荷模型,這與精確的發電機、傳輸線路和變壓器模型在一起,會嚴重的影響電力系統諧波的分析精度,成為整個電力系統仿真計算中提高精度的瓶頸。
當前負荷建模存在的主要問題是:①缺乏通用性,即由某負荷點數據建立的模型對於該點的分析是適合的,但這種模型具有一定特殊性,推廣至其他負荷點將會產生一定的誤差,甚至會產生錯誤的結論。②目前,對電網中大量的負荷建模,還沒有系統的電路理論可循。③負荷受時間、氣候、季節等因素的影響,負荷特性會隨時間的不同而改變,且呈現較大的時變性和隨機性,給電力負荷的建模帶來了很大的困難。④在電力系統變結構特性及變結構負荷情況下,負荷特性會發生非連續行地變化,甚至突變。現有的單一結構負荷模型已無法準確描述電力負荷的變結構特性,獲取實測數據十分困難。
在理論上,通用的諧波負荷模型可由簡單的R、C、L並聯電路附加一個諧波電流源構成。當前的負荷建模常用方法是,利用時域狀態估計技術對通用模型進行參數辨識。但該方法不能消除採樣數據中的噪聲幹擾,參數的辨識準確度差。即是利用數據處理後得到的電壓、電流波形對通用模型進行參數辨識,精度仍不能滿足實際要求。
為了給諧波分析精度提高創造有利條件,本發明結合PLS算法及SVM算法,提出一種根據電壓、電流採樣數據來進行單相負荷諧波建模的方法。本發明在PLS方法的基礎上,通過空間映射消除輸入量相互之間的影響,降低輸入變量維數。利用正交特徵投影克服普通最小二乘回歸的共線性問題,解決了負荷建模的線性與非線性條件限制。在選取特徵向量時強調輸入對輸出的解釋預測作用,去除了回歸無益噪聲,使模型包含最少的變量數。由此快速識別負荷參數,同時建立一種通用性能良好精確度高的單相諧波負荷模型。
把經過PLS方法處理的輸入變量作訓練集用於SVM回歸建模,使該模型具有最好的魯棒性,快速、準確的負荷參數辨識能力。
PLS的主要思想是通過最小化誤差的平方和找到一組數據的最佳函數匹配。用最簡的方法求得一些不可知的真值,而令誤差平方之和為最小。與傳統多元線性回歸模型相比,其特點是能夠在自變量存在嚴重多重相關性的條件下進行回歸建模;允許在樣本點個數少於變量個數的條件下進行回歸建模;在最終模型中將包含原有的所有自變量;更易於辨識系統信息與噪聲(甚至一些非隨機性的噪聲)。
為了研究因變量和自變量的統計關係,取n個樣本觀測點,由此構成了自變量與因變量的數據表X={x1,x2,…,xp}n×p和Y={y1,y2,…,y3}n×p將自變量與因變量分別投射到新空間{w1,w2,…,wk}和{c1,c2,…,ch}上形成新的成分{t1,t2,…,th}n×h和{u1,u2,…,uh}n×h這些新的特徵向量不僅消除了相互之間的影響,而且維數大大降低。
SVM的主要思想有兩點:(1)它基於結構風險最小化理論,在特徵空間中建構最優分割超平面,使得學習器得到全局最優化;(2)對於線性不可分的情況,通過使用非線性映射算法將低維輸入空間線性不可分的樣本轉化為高維特徵空間使其線性可分,從而使得高維特徵空間採用線性算法對樣本的非線性特徵進行線性分析成為可能。
由此可見,根據諧波對負荷的影響建立負荷模型,改進負荷模型算法,提高負荷模型的精度及通用性,對於提高諧波分析精度,以及電力系統諧波潮流計算,具有十分重要的意義。
技術實現要素:
為了解決上述問題,本發明提供了一種基於偏最小二乘法-支持向量機PLS-SVM的通用單相諧波負荷建模方法,所述方法包括:
將電壓和負荷電流錄波數據經過快速傅立葉變換FFT得到電壓電流三角函數表達式;
將所述電壓電流三角函數表達式轉換為Y=ZX+μ的矩陣形式,從而建立基本負荷諧波模型;
對所述母線電壓矩陣X和負荷電流矩陣Y分別進行標準化處理得到數據X0和數據Y0;
對所述數據X0和數據Y0進行至少一次偏最小二乘回歸PLS主成分提取使tm和um的協方差Cov(tm,um)最大,從而得到訓練集樣本數據{Xm(t),Ym(t)};
選擇核函數對上述訓練集樣本數據{Xm(t),Ym(t)}進行支持向量機SVM算法分析並建立拉格朗日優化目標函數和拉格朗日方程;以及
求解拉格朗日問題的約束因子參數α以及負荷參數矩陣Z建立通用單相諧波負荷模型並快速識別出負荷參數。
優選地,在通用單相諧波負荷模型中流過負荷的總電流由表示線性負荷部分的電流iRCL(t)和表示非線性負荷部分的電流ig(t)兩部分組成;其中,電流iRCL(t)包括R、C和L分別對應的元件的電流iR(t)、iC(t)和iL(t),它們之間的關係為:
i(t)=iR(t)+iC(t)+iL(t)+ig(t)。
優選地,其中i(t)能夠用參數R、C、L和ig(t)來表示,並對兩邊求導後將ig(t)表示為傅立葉級數展開形式:
其中,Ah和Bh分別為諧波的電流ig(t)傅立葉級數形式的餘弦分量和正弦分量的幅值;
將母線電壓和負荷電流展開為傅立葉級數形式:
其中,N為所考慮的最高次諧波次數;Uh和Ih分別為第h次諧波電壓和電流的幅值;αh和βh分別為第h次諧波電壓和電流的初相位。
優選地,其中在所述矩陣形式Y=ZX+μ中
其中所述X為母線電壓矩陣,所述Y為負荷電流矩陣,所述Z為負荷參數矩陣,所述μ為測量噪聲矢量。
優選地,其中在標準化處理中Y的標準化矩陣用Y0表示,u1是Y0的第一個主成分,u1=Y0c1,c1是Y0的第一個軸,它是一個單位向量,即||c1||=1;自變量X的標準化矩陣用X0表示,t1是X的第一個主成分,t1=X0k1,k1是X0的第一個軸,同時也是一個單位向量,即||k1||=1。
優選地,其中所述第m主成分提取值為:
其中,Xm-1是變量X的第m-1次提取的標準化訓練集矩陣;Ym-1是變量Y的第m-1次提取的標準化訓練集矩陣;Xm是變量X的第m次提取的標準化訓練集矩陣;Ym是變量Y的第m次提取的標準化訓練集矩陣;tm是X的第m個主成分;pm是矩陣X的回歸係數;rm是矩陣Y的回歸係數。
優選地,其中選擇徑向基函數RBF作為SVM的核函數。
優選地,其中所述拉格朗日優化目標函數為使
的最小值滿足關係式ym(t)=Zxm(t)+μ+ξ;
其中,所述C為懲罰因子,C的取值決定了模型的泛化能力;所述ξ為擬合誤差。
優選地,通過卡羅需-庫恩-塔克KKT條件對所述拉格朗日方程進行分析最終得到:
將所述矩陣α帶入所述負荷參數矩陣Z即可建立通用單相諧波負荷模型:
本發明的有益效果在於:
本發明結合PLS與SVM算法進行諧波條件下單相通用型負荷的模型構建,該模型適用於線性、非線性條件,及各種類型的負荷,通用性好,精確度高。
附圖說明
通過參考下面的附圖,可以更為完整地理解本發明的示例性實施方式:
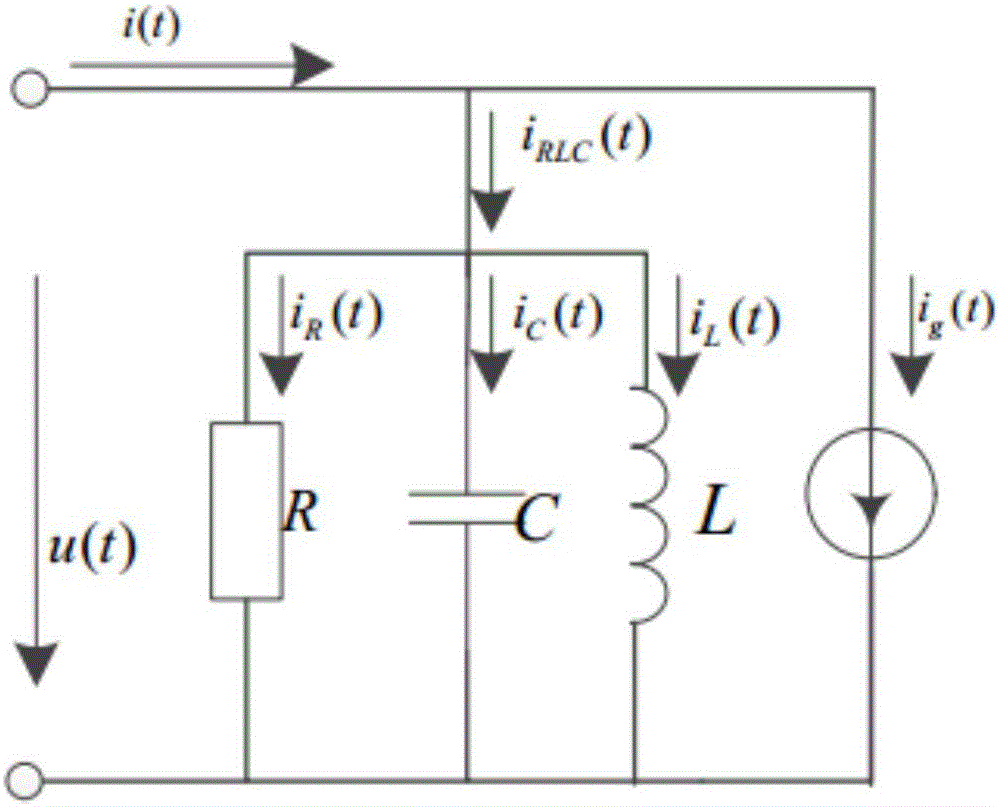
圖1為建立通用單相諧波負荷模型的結構示意圖;
圖2為根據本發明實施方式的基於PLS-SVM的通用單相諧波負荷建模方法200的流程圖;
圖3為根據本發明實施方式的基於PLS-SVM的通用單相諧波負荷建模方法的實例的電路圖。
具體實施方式
現在參考附圖介紹本發明的示例性實施方式,然而,本發明可以用許多不同的形式來實施,並且不局限於此處描述的實施例,提供這些實施例是為了詳盡地且完全地公開本發明,並且向所屬技術領域的技術人員充分傳達本發明的範圍。對於表示在附圖中的示例性實施方式中的術語並不是對本發明的限定。在附圖中,相同的單元/元件使用相同的附圖標記。
除非另有說明,此處使用的術語(包括科技術語)對所屬技術領域的技術人員具有通常的理解含義。另外,可以理解的是,以通常使用的詞典限定的術語,應當被理解為與其相關領域的語境具有一致的含義,而不應該被理解為理想化的或過於正式的意義。
本發明所採用的技術方案是一種基於PLS-SVM的通用單相負荷諧波建模方法,結合PLS算法及SVM算法,提出了一種通過電壓、電流採樣數據來進行單相負荷諧波建模的方法;本發明在PLS方法的基礎上,通過空間映射消除輸入量相互之間的影響,利用正交特徵投影克服普通最小二乘回歸的共線性問題,解決負荷建模線性與非線性條件的限制。在選取特徵向量時強調輸入對輸出的解釋預測作用,去除了回歸無益噪聲,使模型包含最少的變量數。可以快速識別負荷參數,同時建立一種通用性能好、精確度高的單相諧波負荷模型。
圖1為建立通用單相諧波負荷模型的結構示意圖。如圖1所示,R、C、L分別表示負荷中電阻、電容、電感性元件部分的集總效應,表示電力負荷中諧波情況下的線性負荷,其值是在諧波情況下的等值參數,而非基波情況下阻、容、感性元件的等值參數;ig(t)表示電力負荷中的非線性負荷部分。負荷的非線性是產生諧波的主要原因,但諧波的產生不僅由於負荷的非線性特性,而且由於這些諧波會通過電磁感應、靜電感應和傳導方式耦合到系統中,導致系統電壓、電流發生畸變,這種畸變也會對非線性負荷產生影響。在通用單相諧波負荷模型中流過負荷的總電流由表示線性負荷部分的電流iRCL(t)和表示非線性負荷部分的電流ig(t)兩部分組成;其中,電流iRCL(t)包括R、C和L分別對應的元件的電流iR(t)、iC(t)和iL(t),它們之間的關係為:
i(t)=iR(t)+iC(t)+iL(t)+ig(t) (1)
圖2為根據本發明實施方式的基於PLS-SVM的通用單相諧波負荷建模方法200的流程圖。如圖2所示,所述於PLS-SVM的通用單相諧波負荷建模方法200從步驟201處開始,在步驟201將電壓和負荷電流錄波數據經過快速傅立葉變換FFT得到電壓電流三角函數表達式。優選地,其中i(t)能夠用參數R、C、L和ig(t)來表示:
然後對兩邊求導得到:
並將ig(t)表示為傅立葉級數展開形式:
其中,Ah和Bh分別為諧波的電流ig(t)傅立葉級數形式的餘弦分量和正弦分量的幅值;
將母線電壓和負荷電流展開為傅立葉級數形式:
其中,N為所考慮的最高次諧波次數;Uh和Ih分別為第h次諧波電壓和電流的幅值;αh和βh分別為第h次諧波電壓和電流的初相位。
優選地,在步驟202將所述電壓電流三角函數表達式轉換為Y=ZX+μ的矩陣形式,從而建立基本負荷諧波模型。優選地,其中在所述矩陣形式Y=ZX+μ中
其中所述X為母線電壓矩陣,所述Y為負荷電流矩陣,所述Z為負荷參數矩陣,所述μ為測量噪聲矢量。
優選地,在步驟203對所述母線電壓矩陣X和負荷電流矩陣Y分別進行標準化處理得到數據X0和數據Y0。優選地,其中在標準化處理中Y的標準化矩陣用Y0表示,u1是Y0的第一個主成分,u1=Y0c1,c1是Y0的第一個軸,它是一個單位向量,即||c1||=1;自變量X的標準化矩陣用X0表示,t1是X的第一個主成分,t1=X0k1,k1是X0的第一個軸,同時也是一個單位向量,即||k1||=1。
優選地,在步驟204對所述數據X0和數據Y0進行至少一次偏最小二乘回歸PLS主成分提取使tm和um的協方差Cov(tm,um)最大,從而得到訓練集樣本數據{Xm(t),Ym(t)}。
提取第一主成分t1和u1,若要使其分別很好地代表X與Y中數據變異信息,根據主成分分析原理,應該有Var(t1)和Var(u1)均為最大值。另一方面,回歸建模要求對t1和u1有最大解釋能力,由典型相關分析可知,t1與u1相關度應達到最大值,即r(t1,u1)達到最大值。偏最小二乘回歸PLS的目標函數是要求t1與u1協方差Cov(t1,u1)最大,即
為最大值,所以有:
其中,θ2是目標函數,要求取得最大值;k1和c1分別是對應兩矩陣最大特徵值的單位特徵向量。從Y0提取成分u1,u1=Y0c1,||c1||=1。從X0提取成分,t1=X0k1,||k1||=1。由於Y0隻是一個變量,所以c1是一個常數。而由於||c1||=1,所以c1=1,有u1=Y0。
根據(11)式得到:
因為X0和Y0均是單位向量,所以有:
由此X0與Y0對t1的回歸關係為:
式中p1和r1是回歸係數;E1和F1為殘差矩陣。然後進行第二步,以E1和F1分別取代E0和F0繼續上述過程,則可得到第m主成分提取值為:
優選地,其中所述第m主成分提取值為:
其中,Xm-1是變量X的第m-1次提取的標準化訓練集矩陣;Ym-1是變量Y的第m-1次提取的標準化訓練集矩陣;Xm是變量X的第m次提取的標準化訓練集矩陣;Ym是變量Y的第m次提取的標準化訓練集矩陣;tm是X的第m個主成分;pm是矩陣X的回歸係數;rm是矩陣Y的回歸係數。
優選地,在步驟205選擇核函數對上述訓練集樣本數據{Xm(t),Ym(t)}進行支持向量機SVM算法分析並建立拉格朗日優化目標函數和拉格朗日方程。優選地,其中選擇徑向基函數RBF作為SVM的核函數。本發明選擇徑向基函數(Radial Basis Function,RBF),即某種沿徑向對稱的標量函數,作為SVM的核函數。定義為空間中任一點x到之間歐氏距離的單調函數,將低維的線性不可分空間轉化為高維空間實現線性可分。然後在此高維空間中找到最大分類間隔。
且高斯徑向基核函數為
K(x,x')=exp(-||x-x'||2/σ2) (17)
此處誤差定義如下:
其中,S=VI為負荷總的視在功率;SRLC=VIRLC為R、L、C的視在功率;V、I、IRCL分別為負荷電壓有效值、負荷電流有效值和流過R、L、C的總電流的有效值。ε值越接近於0則說明SRCL越接近S,精度也就越高。
因此假設樣本數據第m主成分提取後得到訓練集,在精度ε內滿足式(18)所示的數學模型,即:
|Y-ZX-μ|≤ε (19)
式(19)優化目標在最小化ZTZ/2時可獲得較好推廣能力。
優選地,其中所述拉格朗日優化目標函數為使
的最小值滿足關係式
ym(t)=Zxm(t)+μ+ξ。 (20)
其中,所述C為懲罰因子,C的取值決定了模型的泛化能力;所述ξ為擬合誤差。
優選地,其中所述拉格朗日方程為:
優選地,在步驟206求解拉格朗日問題的約束因子參數α以及負荷參數矩陣Z建立通用單相諧波負荷模型並快速識別出負荷參數。優選地,通過卡羅需-庫恩-塔克KKT(Karush-Kuhn-Tucker)條件
對所述拉格朗日方程進行分析得到:
Zxm(t)+ξ=ym(t)-μ (23)
將式(22)帶入式(23)消去Z,ξ,定義F為消去過程中計算的中間變量,且
則優化問題(20)即轉化為求解如下方程:
其中ym=[ym(1),…,ym(N)]T
E=[1,…,1]T
μ=[μ(1),…,μ(N)]T
求解上述函數式α並帶入式(22)既可以求得所述負荷參數矩陣Z從而快速識別出負荷參數值。
圖3為根據本發明實施方式的基於PLS-SVM的通用單相諧波負荷建模方法的實例的電路圖。如圖3所示的的Matlab/Simulink電路圖模型。頻率為60Hz。電壓源AC Voltage Source為系統電壓,其值為 AC Voltage Source 1為系統中的諧波電壓影響,值為所以系統電壓為已知系統負載的電阻值為2Ω,電容3×10-4F,電感7×10-3H。
通過powergui分析得出負載電流值為:
i(t)=0.4656sin(ωt-133.5°)+0.2477sin(3ωt+73.4°)
將算例中u(t),i(t)作為已知量,識別諧波條件下的負荷參數值。通過流程圖,建立PLS-SVM的諧波負荷模型參數識別程序,辨識得出如下表1所示。
表1電路負荷實際值與識別值對比
由結果即可說明此算法的可行性及實用性。
已經通過參考少量實施方式描述了本發明。然而,本領域技術人員所公知的,正如附帶的專利權利要求所限定的,除了本發明以上公開的其他的實施例等同地落在本發明的範圍內。
通常地,在權利要求中使用的所有術語都根據他們在技術領域的通常含義被解釋,除非在其中被另外明確地定義。所有的參考「一個/所述/該[裝置、組件等]」都被開放地解釋為所述裝置、組件等中的至少一個實例,除非另外明確地說明。這裡公開的任何方法的步驟都沒必要以公開的準確的順序運行,除非明確地說明。
