太空飛行器熱擾動響應仿真分析平臺的製作方法

2023-05-01 05:45:22

本發明屬於高精度太空飛行器設計及動力學仿真與控制技術領域，具體為太空飛行器熱擾動響應仿真分析平臺。

背景技術：

在太空飛行器進出地球陰影區時，空間熱環境發生改變，溫度的劇烈變化不僅會使柔性附件發生較大的熱變形，誘發熱振動，而且擾動力作用還會傳遞到太空飛行器主體上。由於角動量守恆，柔性附件的振動會導致太空飛行器主體姿態發生抖動，進而影響太空飛行器有效載荷的指向精度和姿態穩定度，導致太空飛行器無法正常工作或功能失效。

NASA已觀察到了熱致振動對太空飛行器軌道姿態的影響，國際上也已經發表了諸多因柔性附件發生熱致振動而造成太空飛行器工作失效的例子。隨後一批學者對熱載荷作用對太空飛行器姿態動力學的影響作了研究。對應的相關分析技術已從部件級角度開展了大量的研究工作。然而大多數文獻考慮的都是附件的準靜態熱變形對衛星姿態的影響，即忽略了熱響應的瞬態項，在模型中體現不出因軌道晝夜交替導致的熱誘發振動問題。

從整體系統層面出發分析柔性結構熱致運動對太空飛行器姿態運動的影響，國內外的研究工作並不十分充分。柔性附件熱致動態變形誘發太空飛行器姿態變化的分析與仿真，涉及柔性附件在軌外熱流/角係數、瞬態溫度場、模態、動態變形、耦合響應等多方面的計算，屬於典型多學科交叉問題，單一的仿真分析系統完成計算分析非常困難，專用的仿真軟體系統也非常缺乏。在太空飛行器剛體-附件耦合系統熱-動力學研究領域的較新進展當數Johnston和Thornton的研究。Johnston和Thornton用熱-結構非耦合方法討論了柔性附件熱致振動對太空飛行器動力響應的影響，針對一類由中心剛體和柔性附件構成的衛星系統簡化模型，發展了一種熱-結構動力學非耦合的二維平面運動理論分析方法，研究了衛星柔性附件的熱誘發運動對衛星平面姿態動力學的影響。不足之處是將柔性附件看作簡單梁來處理，對於實際附件的複雜結構形式未做展開討論。

對於指向精度和姿態穩定度要求較高的太空飛行器，如果僅用簡化模型來近似複雜的柔性附件結構，顯然不適合對柔性附件熱致動態變形誘發太空飛行器姿態變化的耦合力學特性進行仿真分析，無法準確預測和評估星載柔性構件熱致振動對太空飛行器姿態的影響。因此，迫切需要建立可解決帶複雜柔性附件結構的太空飛行器熱擾動響應的理論與數值分析模型，發展相應的求解技術和軟體系統。

技術實現要素：

針對上述技術問題，本發明的目的是為解決大型柔性附件熱致動態變形誘發太空飛行器姿態變化的分析與仿真，提出一種星載大型柔性附件與星體耦合的太空飛行器熱擾動響應專用仿真分析平臺。

設計原理是：針對中心剛體-柔性附件類太空飛行器，以等效熱荷載這類內激勵作為擾動源，採用混合坐標法和有限元法對系統進行模化，建立計及熱荷載作用的全星動能和勢能模型，利用Lagrange方法建立太空飛行器熱致微振動耦合動力學模型。經過數值離散後，耦合動力學模型最終表現為一組非線性方程，再利用Newmark方法結合牛頓迭代法進行求解。本發明所針對的研究對象是帶柔性附件的太空飛行器。相比於柔性附件，太空飛行器中心艙體的剛度要大很多，因此可以把中心艙體近似為帶集中質量和轉動慣量的剛體，從而把整個太空飛行器作為中心剛體-柔性附件耦合系統，並忽略中心剛體的平動位移。

具體的技術方案為：

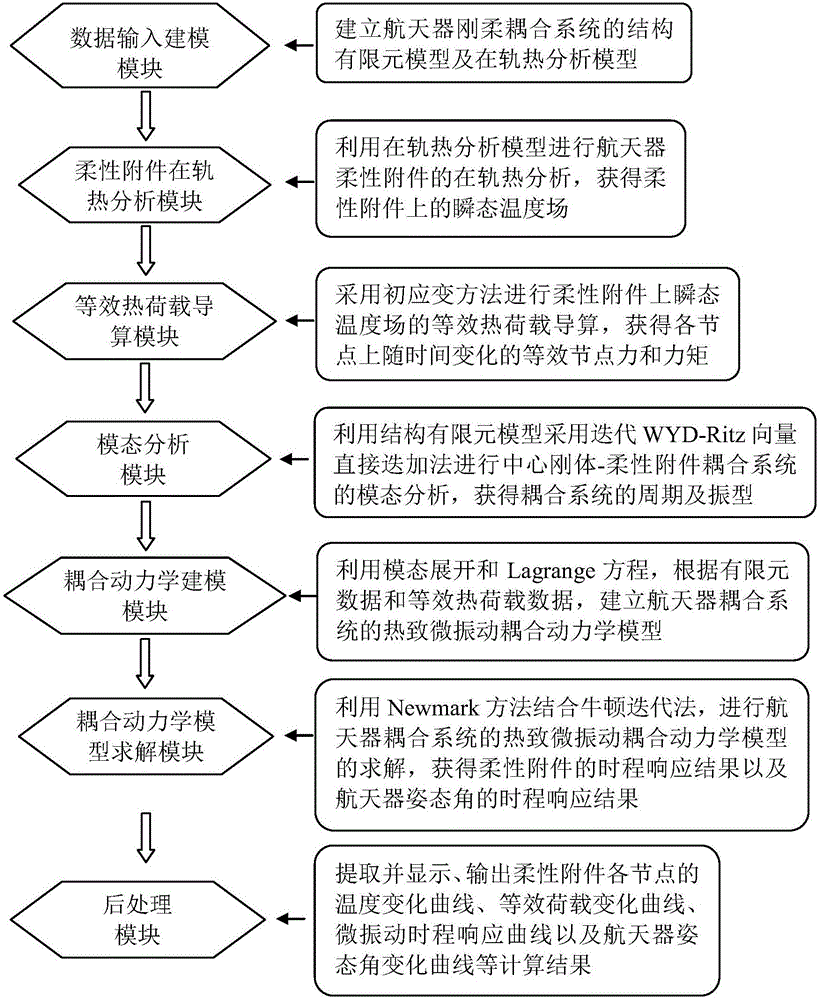
太空飛行器熱擾動響應仿真分析平臺，依次包括數據輸入建模模塊、柔性附件在軌熱分析模塊、等效熱荷載導算模塊、模態分析模塊、耦合動力學建模模塊、耦合動力學模型求解模塊和後處理模塊；

(1)數據輸入建模模塊：利用交互方式結合自動轉換方式建立太空飛行器中心剛體-柔性附件耦合系統的有限元模型以及在軌熱分析模型；

(2)柔性附件在軌熱分析模塊：利用建立的太空飛行器中心剛體-柔性附件耦合系統在軌熱分析模型，進行太空飛行器柔性附件的在軌熱分析，獲得柔性附件上的瞬態溫度場；

柔性附件結構在軌熱分析涉及的傳熱方式主要是熱傳導和熱輻射。本發明著重關注的是太空飛行器進出地球陰影時由於短時間內溫度劇烈變化引發的柔性附件振動問題，因此，柔性附件所受到的外熱流主要考慮太陽輻射熱流。在軌熱分析的熱傳導基本方程與通常的輻射換熱下熱傳導方程是相同的，但增加了軌道計算、角係數計算、外熱流的計算。

(3)等效熱荷載導算模塊：採用初應變方法進行柔性附件上瞬態溫度場的等效熱荷載導算，獲得各節點上隨時間變化的等效節點力和力矩；

利用建立的太空飛行器中心剛體-柔性附件耦合系統的有限元模型，將柔性附件上瞬態溫度場的熱荷載等效為柔性附件上的節點荷載。柔性附件結構中一般包含桁杆、梁、板殼等構件，需要將這些構件單元上所受到的溫度變化等效為隨時間變化的節點力荷載，以便進行下一步的耦合系統微振動時程響應分析。採用有限元方法中的初應變(溫度應變)方法來計算溫度荷載的等效節點力。根據單元的變形模式，桁杆單元的溫度荷載可以等效為軸向力，梁單元的溫度荷載可以等效為軸向力和力矩，板殼單元的溫度荷載可以等效為面內力和面外力矩，可通過單元內的積分完成等效計算。

(4)模態分析模塊：利用結構有限元模型採用迭代WYD-Ritz向量直接迭加法進行中心剛體-柔性附件耦合系統的模態分析，獲得耦合系統的周期及振型；

採用迭代WYD-Ritz向量直接迭加法進行太空飛行器中心剛體-柔性附件耦合系統的模態分析。利用分組移頻、模態誤差收斂判據、細胞稀疏快速直接解法等多項技術提高效率、求解精度及可靠性。目前在普通微機上特徵值問題的解題規模可達30到50萬個自由度，可精確地解出多至幾百個低端模態。模態誤差收斂判據使模態分析的過程變得平穩。測試結果表明，模態誤差比特徵值誤差更能反映特徵值問題計算的精度。在計算較多模態時，模態誤差應該作為首選的收斂判據。

(5)耦合動力學建模模塊：利用模態展開和Lagrange方程，根據有限元數據和等效熱荷載數據，建立太空飛行器耦合系統的熱致微振動耦合動力學模型；

柔性附件與星體耦合系統的動能表達式為：

式中M為太空飛行器系統質量；用模態坐標對上式中柔性附件的結構變形進行模態展開後，太空飛行器柔性附件與星體耦合系統的動能方程為：

式中Φ、η分別為柔性附件結構的模態矩陣和模態坐標陣；

為太空飛行器系統靜距；

為太空飛行器系統相對質心的轉動慣量陣；

為柔性附件結構熱致振動對太空飛行器平動的柔性耦合係數矩陣；

為柔性附件結構熱致振動對太空飛行器轉動的柔性耦合係數矩陣；

為柔性附件結構的剛體模態陣；

組集柔性附件結構所有單元應變能後，則計及熱荷載效應的太空飛行器勢能方程為：

式中K、rT分別為柔性附件結構的剛度陣和熱荷載陣，Λ為附件在模態空間中的剛度陣；

太空飛行器系統的Lagrange函數表示為：

根據準坐標形式的Lagrange方程，不考慮太空飛行器的平動，並忽略一些高階項，則帶單個柔性附件的太空飛行器中心剛體-柔性附件耦合系統的耦合動力學方程最終簡化為：

上式中的係數矩陣可以利用耦合系統有限元模型的幾何信息、質量矩陣以及固有頻率和振型等得到，熱荷載等效節點力也可以在獲得溫度場數據之後利用初應變法由等效熱荷載導算模塊得到。

(6)耦合動力學模型求解模塊：利用Newmark方法結合牛頓迭代法，進行太空飛行器耦合系統的熱致微振動耦合動力學模型的求解，獲得柔性附件的時程響應結果以及太空飛行器姿態角的時程響應結果；

將耦合動力學方程改寫為：

定義系統的狀態變量為：

則耦合動力學方程可表示為：

採用Newmark方法在時間域離散，其數值格式為：

其中，

當δ≥0.5,γ≥0.25(0.5+δ)2時，算法是無條件穩定的，這樣就允許使用較大的時間步長，例如選為結構最小周期的若干分之一。因此Newmark方法可以用來求解時程較長的時程響應，且較大的時間步長還可以略去高階不精確特徵解對系統響應的影響。在本發明中，選擇δ＝0.5,γ＝0.25。

耦合動力學方程為非線性方程組，在每個時間步之內需要使用牛頓迭代法進行迭代求解，其迭代格式為：

將上式代入荷載項中，並將之分解為兩部分：

其中，與當前時間步要求未知量qn+1有關，與上一時間步已知量有關。重新整理後，記作：

Ψ(qn+1)＝F

採用牛頓迭代法，其求解的迭代公式為：

在實際計算中，每一個時間步內只需要迭代3-5次即可收斂。

在求解動力學耦合方程時，由於採用了振型疊加法，在獲得模型的模態信息之後大大降低了方程組的階數，同時採用無條件穩定的Newmark方法求解動力響應，允許使用較大的時間步長，有助於模擬更長的時間或者求解更大規模的問題，在每一步的迭代中收斂也很快，說明了求解算法的高效和可靠性。

(7)後處理模塊：提取並顯示、輸出柔性附件各節點的溫度變化曲線、等效荷載變化曲線、微振動時程響應曲線以及太空飛行器姿態角變化曲線等計算結果。

後處理模塊主要是根據用戶要求提取並顯示、輸出相關的計算結果，例如柔性附件上各節點的溫度變化曲線、等效荷載變化曲線、柔性附件微振動時程響應曲線、太空飛行器的姿態角變化曲線。

本發明提供的太空飛行器熱擾動響應仿真分析平臺，以高指向精度太空飛行器為工程背景，建立了星載大型柔性附件與星體耦合動力學模型，提出了一種星載大型柔性附件與星體耦合響應專用仿真分析平臺。該仿真分析平臺可以用來求解帶複雜柔性附件的太空飛行器由其柔性附件熱致動態變形所誘發的姿態變化，能夠為實際情形下帶柔性附件太空飛行器熱致振動響應的預測和評估提供一種簡單有效的模型、方法和工具，可以作為實際衛星設計過程中的參考。

附圖說明

圖1為本發明結構示意圖；

圖2為實施例的LEO太空飛行器簡化結構示意圖；

圖3為實施例的端部角點迎光面、背光面溫度變化曲線及其溫差變化曲線；

圖4為實施例的端部節點的等效力矩曲線；

圖5為實施例的端部角點沿軸向線位移；

圖6為實施例的端部角點繞軸向角位移；

圖7為實施例的中心剛體姿態角變化曲線。

具體實施方式

為了進一步說明本發明的目的和優點，下面結合附圖和具體實例對本發明作進一步的說明。

本實施例的太空飛行器熱擾動響應仿真分析平臺結構如圖1所示，依次包括數據輸入建模模塊、柔性附件在軌熱分析模塊、等效熱荷載導算模塊、模態分析模塊、耦合動力學建模模塊、耦合動力學模型求解模塊和後處理模塊。

採用如圖2所示的帶有單翼太陽陣結構的低地球軌道(LEO)太空飛行器為研究對象。針對從日照區進入陰影區劇烈變化熱環境引起的柔性太陽陣結構動態變形及星體姿態振動響應進行了數值仿真分析。

利用本發明提出的平臺，按以下步驟實施數值仿真：

(1)利用數據輸入建模模塊建立耦合系統的有限元模型以及在軌熱分析模型；

(2)利用柔性附件在軌熱分析模塊進行太陽電池陣的在軌熱分析，獲得太陽電池陣柔性結構在軌期間特別是進出地球陰影區時的瞬態溫度場數據；

(3)利用等效熱荷載導算模塊，將上一步驟獲得的瞬態溫度場數據等效為施加到太陽電池陣柔性結構節點上的熱荷載；

(4)利用模態分析模塊，對耦合系統模型進行模態分析，獲取前20階模態；整個太空飛行器作為中心剛體-柔性附件耦合系統，只約束中心點的三個平動自由度；

(5)利用耦合動力學建模模塊，根據耦合系統的有限元數據和等效熱荷載數據，建立太空飛行器耦合系統的熱致微振動耦合動力學模型；

(6)利用耦合動力學模型求解模塊，進行耦合系統的熱致微振動耦合動力學模型的求解，獲得柔性附件的時程響應結果以及太空飛行器姿態角的時程響應結果。

圖3為太陽電池陣端部角點在進入地球陰影時刻對應的溫度變化曲線及溫差變化曲線。從圖3中可以發現，太陽電池陣結構溫差變化曲線在開始進入地球陰影后經過大約20s的時間趨向於穩定。因此，可認定該太陽電池陣的熱結構響應時間近似為20s，同時其結構響應時間(第一階模態對應的周期)為8.63s，二者相差不大。該柔性太陽陣結構在進入地球陰影期間有可能發生熱致動態變形。

圖4為該太陽電池陣端部角點的等效力矩曲線。以圖示0s時刻為初始狀態，並假定此時的位移、等效熱荷載為零。通過耦合動力學方程求解可獲得太陽陣端部角點和中心剛體姿態對應的熱致響應曲線，分別見圖5、圖6和圖7。

從上述仿真分析結果可知：空間熱環境的劇烈變化引起了該衛星系統的振動響應。其中，太陽陣結構角點軸向變形最大幅值為0.95mm，彎曲變形最大幅值在0.54arcsec，星體姿態角產生最大接近於0.042arcsec的變化，太陽電池陣熱致微振動響應量級較小，但誘發了衛星姿態的顫振響應。