質子交換膜燃料電池瞬態過程模型建立的方法與流程
2023-04-30 20:30:36 2
本發明屬於電化學燃料電池領域,具體涉及一種用於對燃料電池的性能進行預測計算的方法。
背景技術:
目前我國交通能耗約佔社會總能耗的20%,且比例呈逐年上升,城市內汽車尾氣更被認為是造成空氣汙染和產生霧霾的重要原因。燃料電池以氫氣為燃料,生成物為水,所以質子交換膜燃料電池被視為汽車的理想動力源,是解決尾氣排放問題的有效手段。
汽車在城市運行過程中發動機處於變工況運行,燃料電池動態響應較慢和變工況下燃料電池性能衰退是燃料電池應用於車載動力的最大難題。測試燃料電池的瞬態性能和壽命,已成為考查電池設計是否合理、技術能否成熟的重要鑑定標準。通過對電池內反應物的運輸和水管理方法進行仿真(電池變工況過程),能預測該電池在瞬態過程中的性能變化,還能從反應物和水輸運過程探明性能波動和衰退的原因。本發明所提出的質子交換膜燃料電池瞬態過程仿真的建模方法,主要應用於燃料電池的開發和測試階段,為提升電池瞬態性能提出數據依據。
技術實現要素:
本發明的目的是,提出一種建立質子交換膜燃料電池瞬態過程模型仿真的方法,為研究變工況下,質子交換膜燃料電池反應氣體、水的瞬態過程和電池瞬態性能提供方法。
構建的模型包括電池內水的瞬態響應、反應氣體的瞬態響應、電壓瞬態響應三部分性能預測計算。
沿電池垂直於極板方向,求得變工況下每一時刻電池內水瞬態變化、反應氣體瞬態變化和電壓瞬態變化,然後據此求得對應時刻的燃料電池輸出電壓,由此預測電池瞬態性能,其具體步驟為:
(1)電池內水瞬態變化過程
該過程包括:陽極催化層水蒸氣和陰極催化層液態水。
陽極催化層水蒸氣:
陰極催化層液態水:
式中,微孔層和催化層間的有效水蒸氣擴散率與微孔層和催化層間的滲透率kl,mpl-cl分別為:
由式1-1求出當前時刻陽極催化層水蒸氣濃度由式1-2求出陰極催化層液態水體積分數將各個時刻的陽極水蒸氣濃度和陰極液態水體積分數繪製成曲線,得到瞬態過程中水分布的變化。
(2)反應氣體瞬態變化過程
該過程包括:陽極催化層氫氣濃度和陰極催化層氧氣濃度。
陽極催化層氫氣濃度:
陰極催化層氧氣濃度:
式中,微孔層和催化層間的有效氫氣擴散率與微孔層和催化層間的有效氧氣擴散率分別為:
由式2-1求出當前時刻陽極催化層氫氣濃度由式2-2求出當前時刻陰極催化層氧氣濃度將各個時刻的氫氣濃度和氧氣濃度繪製成曲線,得到瞬態過程中反應氣體濃度的變化。
(3)電壓瞬態變化過程
電池輸出電壓為:
vout=erev-ηohm-ηact,a-ηact,c3-1
式中:vout為電池輸出電壓;erev為電化學反應可逆電壓;ηohm為歐姆損失;ηact,a為陽極活化損失;ηact,c為陰極活化損失,
電化學反應可逆電壓erev由能斯特方程求得:
陽極和陰極的活化損失分別為:
將式2-1求得的陽極催化層氫氣濃度帶入式3-3求出陽極活化損失,將式2-2求得的陰極催化層氧氣濃度帶入式3-4求出陰極活化損失,
歐姆損失:
式中質子交換膜電導率:
由式3-1求得每一時刻電池輸出電壓,將每個時刻輸出電壓繪製成曲線得到瞬態過程中輸出電壓的變化。
本發明的特點及產生的有益效果是:從燃料電池電化學機理、水管理和傳質分析角度建立全電池瞬態模型,具有對燃料電池性能分析準確性高,研究性強的特點,同時採用顯式解法以保證高計算效率。該模型可用於預測電池在瞬態過程中的性能變化,燃料電池在變工況運行下達到穩定的響應時間,還能從反應物和水輸運過程探明燃料電池性能波動和衰退的原因。
附圖說明
圖1為實施例中電流密度由1000a/m2變為5000a/m2過程中電壓隨時間的變化特徵。
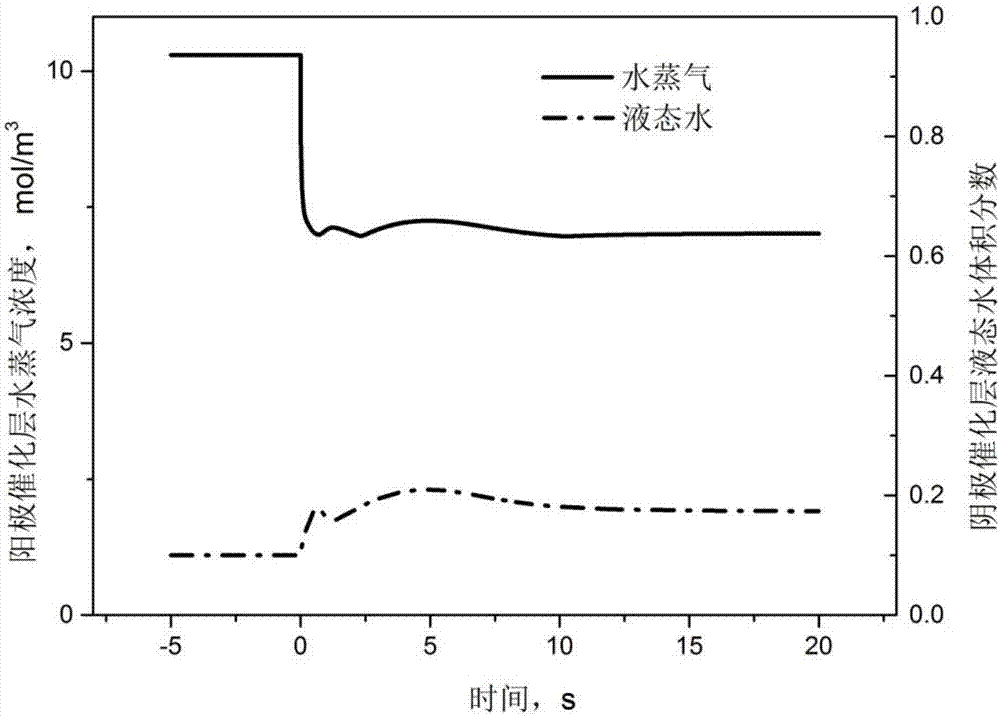
圖2為實施例中電流密度由1000a/m2變為5000a/m2過程中水分布隨時間的變化特徵。
圖3為實施例中電流密度由1000a/m2變為5000a/m2過程中反應氣體濃度隨時間的變化特徵。
具體實施方式
以下通過具體實施例對本發明的方法步驟過程作進一步的說明,需要說明的是本實施例是敘述性的,而不是限定性的,不以此限定本發明的保護範圍。
質子交換膜燃料電池瞬態過程模型建立的方法,沿電池垂直於極板方向,求得變工況下每一時刻電池內水瞬態變化、反應氣體瞬態變化和電壓瞬態變化,然後據此求得對應時刻的燃料電池輸出電壓,由此預測電池瞬態性能。其具體步驟為:
(1)電池內水瞬態變化過程
該過程包括:陽極催化層水蒸氣和陰極催化層液態水。
陽極催化層水蒸氣:
式中:為上一時間步陽極微孔層內水蒸氣濃度;為上一時間步陽極催化層內水蒸氣濃度;為微孔層和催化層間的有效水蒸氣擴散率;δmpl為微孔層厚度;δcl為催化層厚度;δm為質子交換膜厚度;ρl為液態水密度;為水的摩爾質量;kl,m為質子交換膜的滲透率;μl為水的動力粘度;為上一時間步陽極催化層液壓;為上一時間步陰極催化層液壓;dm為膜態水擴散率;ρdry為幹態膜密度;ew為質子交換膜的當量質量;為上一時間步陽極催化層膜水量;上一時間步陰極催化層膜水量;nd為電滲拖拽係數;i為電流密度;f為法拉第常數;εacl為陽極催化層孔隙率;為上一時間步陽極催化層液態水體積分數;為當前時間步陽極催化層水蒸氣濃度;δt為時間步長。
陰極催化層液態水:
式中:kl,mpl-cl為微孔層和催化層間的滲透率;為當前時間步陰極催化層內液態水體積分數;為上一時間步陰極催化層內液態水體積分數。
其中,微孔層和催化層間的有效水蒸氣擴散率與微孔層和催化層間的滲透率kl,mpl-cl分別為:
水蒸氣絕對擴散率:dvap=2.982×10-5(t/333.15)1.5。
由式1-1求出當前時刻陽極催化層水蒸氣濃度由式1-2求出陰極催化層液態水體積分數將各個時刻的陽極水蒸氣濃度和陰極液態水體積分數繪製成曲線,得到瞬態過程中水分布的變化。
即給定初始時刻陽極催化層內水蒸氣濃度和陰極催化層內液壓,不斷求得下一時刻相應的值,得到變工況過程水的變化過程。
(2)反應氣體瞬態變化過程
該過程包括:陽極催化層氫氣濃度和陰極催化層氧氣濃度。
陽極催化層氫氣濃度:
式中:為上一時間步陽極微孔層內氫氣濃度;為上一時間步陽極催化層內氫氣濃度;為微孔層和催化層間的有效氫氣擴散率;為當前時間步陽極催化層氫氣濃度。
陰極催化層氧氣濃度:
式中:為上一時間步陰極微孔層內氧氣濃度;為上一時間步陰極催化層內氧氣濃度;為微孔層和催化層間的有效氧氣擴散率,為當前時間步陰極催化層氧氣濃度。
其中,微孔層和催化層間的有效氫氣擴散率與微孔層和催化層間的有效氧氣擴散率分別為:
氫氣絕對擴散率:
氧氣絕對擴散率:
由式2-1求出當前時刻陽極催化層氫氣濃度由式2-2求出當前時刻陰極催化層氧氣濃度將各個時刻的氫氣濃度和氧氣濃度繪製成曲線,得到瞬態過程中反應氣體濃度的變化。
即給定初始時刻陽極催化層內氫氣濃度和陰極催化層內氧氣濃度,不斷求得下一時刻相應的值,得到變工況過程反應氣體的變化過程。
(3)電壓瞬態變化過程
電池輸出電壓為:
vout=erev-ηohm-ηact,a-ηact,c3-1
式中:vout為電池輸出電壓;erev為電化學反應可逆電壓;ηohm為歐姆損失;ηact,a為陽極活化損失;ηact,c為陰極活化損失。
電化學反應可逆電壓erev由能斯特方程求得:
式中:δg為吉布斯自由能變;f為法拉第常數;δs為熵變;r為理想氣體常數;t為工況溫度;tref為參考溫度;為氫氣分壓力;為氧氣分壓力。
陽極和陰極的活化損失分別為:
式中:α為電荷傳輸係數;n為單位反應中傳輸的電子數;為陽極反應參考交換電流密度;為陰極反應參考交換電流密度;為參考氧氣濃度;為參考氧氣濃度。
將式2-1求得的陽極催化層氫氣濃度帶入式3-3求出陽極活化損失,將式2-2求得的陰極催化層氧氣濃度帶入式3-4求出陰極活化損失,
歐姆損失:
式中:δbp為極板厚度;δgdl為擴散層厚度;σbp、σgdl、σmpl、σcl、σm依次為極板、擴散層、微孔層、催化層和質子交換膜的電導率。
其中質子交換膜電導率:
λ為質子交換膜中膜態水含量,
式中a為水活度:
由式3-1求得每一時刻電池輸出電壓,將每個時刻輸出電壓繪製成曲線得到瞬態過程中輸出電壓的變化。
即由步驟(1)、(2)中求得每一時刻的水含量和反應氣體濃度,相應的求得每一時刻的輸出電壓,得到變工況過程輸出電壓的變化過程。
具體實施例以及涉及到主要參數:
電池初始狀態下以電流密度i=1000a/m2穩定工作,在0時刻電流密度改變為i=5000a/m2。
在i=1000a/m2初始狀態下陽極催化層水蒸氣濃度為:陰極催化層液態水體積分數為:
陽極催化層氫氣濃度為陰極催化層氧氣濃度為:
溫度t=343.15k,陰陽極入口氣壓均為1atm,陽極氫氣和陰極空氣供給化學計量比方式分別為1.5和2,陰陽極進氣均為完全加溼rh=100%。
電池設計參數包括質子交換膜採用nafion212,擴散層、微孔層、催化層厚度依次為2×10-4、0.3×10-4、0.1×10-4m;孔隙率依次為0.6、0.4、0.3;流道長0.1m,極板面積2×10-4m2。
模型採用顯式解法以保證計算速率,並選取小時間步長以保證計算精度,時間步長δt=10-6s。
如前所述,質子交換膜燃料電池瞬態過程模型包括水的瞬態響應,反應氣體的瞬態響應和電化學反應瞬態性能三個步驟:
(1)水瞬態變化過程
0+δt時刻陽極催化層內水蒸氣濃度:
0+δt時刻陰極催化層內液態水體積分數:
(2)反應氣體變化過程
0+δt時刻陽極催化層內氫氣濃度:
0+δt時刻陰極催化層內氧氣濃度:
(3)電壓瞬態變化:
以下過程為求得0+δt時刻電池輸出電壓:
可逆電壓:
陽極活化損失:其中0+δt時刻催化層內氫氣濃度ηact,a=0.07603285584v。
陰極活化損失:其中0+δt時刻催化層內氧氣濃度ηact,c=0.3138855166v。
質子交換膜水活度
質子交換膜膜態水含量λ=14.0+1.4(a-1)=14.10045156。
質子交換膜質子電導率:
計算歐姆損失
計算輸出電壓vout=erev-ηohm-ηact,a-ηact,c=0.6923916296v。
經過以上步驟求得0+δt時刻的輸出電壓、反應氣體濃度和水含量,依次求解之後每一時刻的情況,直到輸出電壓和物質濃度達到下一時間步的值與當前相差小於0.1%,則視為電池達到當前的穩定狀態。
3個附圖為具體實施算例的結果:0時刻前燃料電池在電流密度為1000a/m2下穩定工作,0時刻時輸出電流突變為5000a/m2。圖1為該過程中電壓隨時間的變化曲線,電壓瞬間降低,波動中產生過調效果後小幅上升,經過2.4秒電壓達到穩定;圖2為該過程中水分布隨時間的變化曲線,電池內水分布響應所需時間較長,催化層內水蒸氣或液態水均是在10秒後方達到穩定,此時電池電壓已相對穩定;圖3為該過程中反應氣體濃度隨時間的變化,由於氣體具有較高的擴散率,陽極催化層內氫氣和陰極催化層內氧氣濃度均在極短時間(零點幾秒)內達到穩定狀態。可見在保證反應氣體供應條件下,反應氣體動態響應較快,並不是影響電壓波動的主要原因。
