一種構建金屬薄板成形極限應力圖的方法與流程
2023-04-27 19:40:41 1
本發明屬於金屬板料成形技術領域,特別涉及一種構建金屬薄板成形極限應力圖的方法。
背景技術:
在板料成形領域,成形極限圖(Forming Limit Diagram,FLD)是評價板料成形性能的重要方法,其反映了板料在發生塑性失穩時的極限應變。FLD為方便地研究板料成形極限和評價拉伸失穩理論提供了基礎。然而,目前通過實驗或是理論推導確定的FLD大都是由線性或近似線性的應變路徑得到的,實際板料的衝壓,特別在是成形較複雜的零件或是多工序成形的情況下,往往偏離了線性應變路徑,導致無法準確判斷板料的失穩現象。
研究發現,極限應變只由應力狀態決定,失穩點的應力與應變路徑無關。通過建立基於應力為判據的成形極限應力圖(Forming Limit Stress Diagram,FLSD),可以用來解決FLD應用的局限性。
然而,由於在板料成形過程中各點的應力難以測量,目前無法通過直接測量的方法獲得板料的成形極限應力圖。因此,迫切需要一種能簡單、方便地構建金屬薄板成形極限應力圖的方法。
技術實現要素:
本發明的目的在於提供一種構建金屬薄板成形極限應力圖的方法,解決了板料成形過程中應力難以測量的問題。實現了獲得的成形極限應力圖準確評價複雜零件實際成形過程中的頸縮和破裂問題,並可同時用於有限元分析過程中板料失穩的判斷。
一種構建金屬薄板成形極限應力圖的方法,具體步驟及參數如下:
1、對採用冷軋或熱軋方法生產的厚度為0.2mm~3mm的金屬薄板材料採用電解液腐蝕法印製網格或散斑;
2、對板料施加預應變,所實現的應變路徑包括:單向拉伸、平面應變和雙向等拉;單向拉伸預應變通過採用三軸加載試驗機對寬板進行拉伸來實現,平面應變預應變及雙向等拉預應變通過採用半球形剛性凸模脹形試驗來實現;
3、通過在線或離線應變測量系統測量預應變試樣的主應變和次應變;
4、從預變形的試樣上採用線切割的方式分別製備第二階段單向拉伸、平面應變和雙向等拉變形的試樣,並採用半球形剛性凸模脹形直至試樣發生頸縮或破裂;
5、採用在線或離線應變測量系統測量第二階段變形試樣的主應變和次應變;
6、根據獲得的兩個階段的應變值,採用相應的屈服準則及轉換公式獲得成形極限應力圖,具體轉換公式如下:
(1)
(2)
式中,(ε1f,ε2f)為預應變,(ε1f-ε1i,ε2f-ε2i)為第二階段應變,表達式為等效應力,和α(ρ)隨板料塑性變形所遵循的屈服準則的不同而不同,而σ1和σ2則為轉換後的兩個主應力。
本發明的基本原理,是在實驗中分別測定每段線性應變路徑下的應變分量,計算相應應變路徑下的等效應變。將每段的等效應變相加得到極限狀態下等效應變。結合材料的等效應力和等效應變關係式可以計算極限狀態下等效應力,最後根據塑性變形的應力應變關係的增量理論得到極限狀態下的應力分量。
本發明的優點在於:
1、通過本發明的試驗方法,可快速、準確地獲得金屬薄板成形極限應力圖。
2、測定每段線性應變路徑下的應變分量,並結合材料的等效應力和等效應變關係式,獲得成形極限應力圖,可以解決應力難以直接測量的問題。
附圖說明
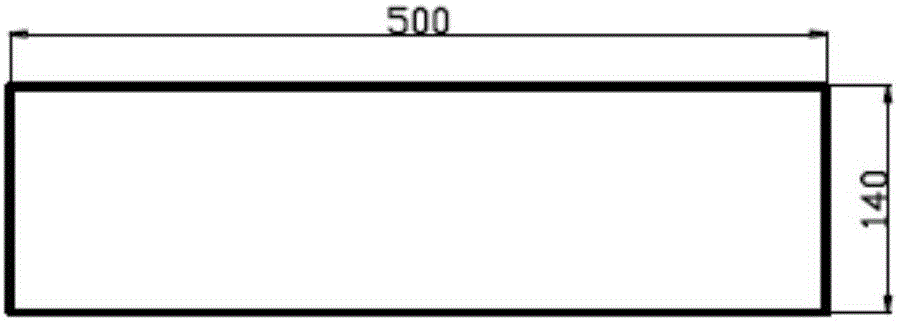
圖1為第二階段為單向拉伸的單拉預應變試樣尺寸示意圖。
圖2為第二階段為平面應變的單拉預應變試樣尺寸示意圖。
圖3為第二階段為雙向拉伸應變的單拉預應變試樣尺寸示意圖。
圖4為單向拉伸試樣尺寸示意圖。
圖5為平面應變試樣尺寸示意圖。
圖6為雙向拉伸試樣尺寸示意圖。
圖7為脹形試驗原理圖。
圖8為成形極限應力圖。
具體實施方式
實施例1
下面結合附圖說明本發明的具體實施方式:
1、將厚度為0.9mm的DP780+Z高強鋼按照如圖1、圖2、圖3所示的尺寸切割成預單向拉伸試樣,按照圖5的尺寸切割成預平面應變試樣,按照圖6的尺寸切割成預雙向拉伸應變試樣;
2、對試樣中間變形均勻區域採用電解液腐蝕法印製網格或散斑;
3、對試樣進行預應變。預單向拉伸通過三軸加載試驗機實現,對圖1、圖2、圖3所示的試樣進行預定應變量的單向拉伸,預平面應變和預雙向拉伸應變採用圖7示意的半球形剛性凸模脹形試驗裝置進行。採用離線或在線應變測量系統測得預應變試樣的主應變ε1i和次應變ε2i。
4、對試樣進行第二階段變形。從預變形試樣上採用線切割製備圖4、圖5、圖6所示的試樣。第二階段變形包括單向拉伸、平面應變和雙向等拉,採用半球形剛性凸模脹形直至試樣發生頸縮或破裂。採用離線或在線應變測量系統測得預應變試樣的主應變ε1f和次應變ε2f。
5、計算成形極限應力圖的基本原理,是在實驗中分別測定每段線性應變路徑下的應變分量,計算相應應變路徑下的等效應變。將每段的等效應變相加得到極限狀態下等效應變。結合材料的等效應力和等效應變關係式可以計算極限狀態下等效應力,最後根據塑性變形的應力應變關係的增量理論得到極限狀態下的應力分量。對FLD轉換為FLSD進行如下推導。
忽略板料的厚向應力,即σ3=0,處於平面應力狀態,設板面內的應力比α=σ2/σ1。塑性理論定義了等效應力它是應力張量各分量和材料參數的函數,對於面內各向同性材料,等效應力可以表達為:基於兩個應力分析之間的關係,等效應力可用σ1和α表示為:
公式一:式中為材料參數的函數。
同理,設板面內的應變增量比則等效應變為:
公式二:式中,λ(ρ)為等效應變增量與較大真實應變增量的比值。
基於應力應變本構關係,等效應力與等效應變存在以下關係:
公式三:
則α與ρ之間的關係為:
公式四:α=α(ρ)
通過以上的假設和公式,可以定義出從應變狀態到應力狀態的轉換關係如下:
公式五:
公式六:
式中,(ε1f,ε2f)為預應變,(ε1f-ε1i,ε2f-ε2i)為終應變,表達式採用Hollomon應變硬化式,等效應力為:
公式七:
和α(ρ)隨板料塑性變形所遵循的屈服準則的不同而不同,而σ1和σ2則為轉換後的兩個主應力。
Hill二次厚向異性塑性準則是Hill屈服準則的一個特例,此時,等效應力是主應力σ1和σ2以及厚向異性係數r的函數:
公式八:
等效應變方程為:
公式九:
等效應力與最大主應變之比為:
公式十:
等效應變與最大主應變之比為:
公式十一:
ρ與α之間的關係為:
公式十二:
公式十三:
把公式九、十、十一帶入式五、六、七即可得到應變成形極限圖到應力成形極限圖的轉換關係。DP780+Z強度因子K=1274,r=0.75,n=0.16,將雙線性應變路徑下的預應變主應變、次應變和破裂時的主應變、次應變帶入公式得到圖8所示的FLSD。
以上所述僅是本發明的優選實施方式,並非對本發明作任何形式上的限制,本技術領域的技術人員來說,利用上述技術原理進行若干修改,均落在本發明的保護範圍內。
