SAR海面仿真方法及裝置與流程
2023-05-25 00:55:01 3
本申請涉及合成孔徑雷達(sar:syntheticapertureradar)技術領域,尤其涉及sar海面仿真方法及裝置。
背景技術:
上升流是指海水由深層向海表淺層垂直運動的一種海洋現象,一般認為風的驅動是上升流發生的動力來源。上升流的存在能夠將深水區豐富的營養鹽帶到海表淺層,從而促進浮遊生物的光合作用。因此,通常情況下,上升流海區具有較高的初級生產力,較高的初級生產力往往能促成漁場的形成,南美洲的秘魯漁場及中國舟山漁場均處於上升流海區。研究表明,僅佔海洋面積5%的五個主要上升流漁場提供了全球25%的漁獲量。上升流通過營養鹽的輸運,不僅能夠形成漁場,對全球碳循環也存在重要意義,並且通過多種方式影響海洋的營養物質、熱量以及汙染物等的交換,對海洋運動也產生了深遠的影響,與此同時,也影響著人類活動。
合成孔徑雷達是一種主動式微波成像雷達,通過測量和處理海面的後向散射信號,獲得海面的後向散射強度圖像,換而言之,sar能夠探測海面的粗糙度並成像。由於sar具有高空間解析度、全天時、全天候的特點,即使在惡劣條件下,sar圖像也能夠包含詳細的海面空間信息,能夠彌補可見光和紅外傳感器等其他傳感器的不足。然而,基於sar單一提取海面風場或海浪信息的方法實現sar海面仿真,仍然存在sar海面仿真結果準確性較差的問題,無法滿足人們對海面仿真有效性的需求。
技術實現要素:
本申請實施例提出了sar海面仿真方法及裝置,以解決現有sar海面仿真結果準確性較差的技術問題。
在一個方面,本申請實施例提供了sar海面仿真方法,其特徵在於,包括:
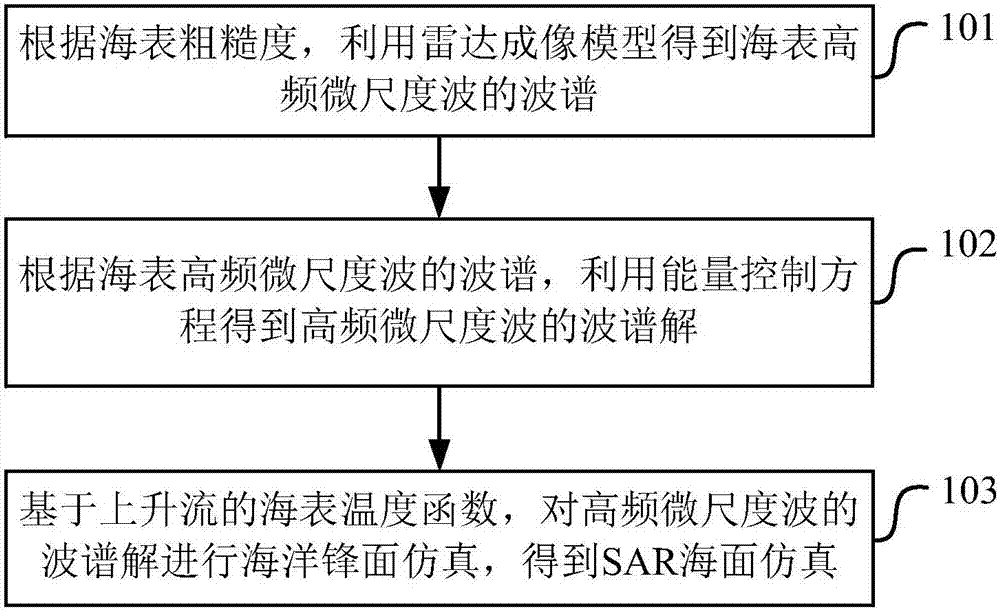
根據海表粗糙度,利用雷達成像模型得到海表高頻微尺度波的波譜;
根據海表高頻微尺度波的波譜,利用能量控制方程得到高頻微尺度波的波譜解;
基於上升流的海表溫度函數,對高頻微尺度波的波譜解進行海洋鋒面仿真,得到sar海面仿真。
在另一個方面,本申請實施例提供了sar海面仿真裝置,其特徵在於,包括:
波譜模塊,用於根據海表粗糙度,利用雷達成像模型得到海表高頻微尺度波的波譜;
波譜解模塊,用於根據海表高頻微尺度波的波譜,利用能量控制方程得到高頻微尺度波的波譜解;
仿真模塊,用於基於上升流的海表溫度函數,對高頻微尺度波的波譜解進行海洋鋒面仿真,得到sar海面仿真。
優選地,所述波譜模塊包括:
通過量化海表粗糙度,獲得雷達信號的歸一化後向散射截面強度,所述海表粗糙度包括大尺度波傾斜造成的均方斜率、波浪破碎,以及布拉格波;
歸一化後向散射截面強度的計算公式為,
其中,代表布拉格波散射,代表由均方斜率構成的雷達信號的鏡面反射,代表大尺度波的波浪破碎。
優選地,所述波譜解模塊包括:
高頻微尺度波的波譜具有能量平衡狀態,能量控制方程為,
高頻微尺度波的波譜解計算公式為,
優選地,所述仿真模塊包括:
根據上升流的海表溫度函數,利用拖曳係數確定海表風摩擦速度;
根據海表風摩擦速度,計算出所述海表溫度函數對應的風應力值;
在sar對海面的觀測角在20°~70°時,根據所述風應力值,對高頻微尺度波的波譜解進行布拉格仿真,得到後向散射截面強度;
其中,海表溫度函數為,
t(x)=1x<w1
t(x)=t+k1xw1<xw2。
優選地,所述對高頻微尺度波的波譜解進行布拉格仿真,得到後向散射截面強度的步驟包括:
當波長λb=λr/2sinθ時,該波長λb的微尺度波為布拉格波,利用布拉格共振散射機制計算後向散射截面強度,計算公式為,
其中,kr=2π/λr,kb=2π/λb分別為雷達波波數和布拉格波波數;gpp為極化函數,ψ為微尺度波波譜。
優選地,還包括:
一維仿真模塊,用於在sar對海面的觀測角在20°~70°時,根據基於上升流的海表溫度函數和流場函數,對高頻微尺度波的波譜解進行海洋鋒面仿真,得到一維sar海面仿真;
其中,海表溫度函數為,
t(x)=1x<w1
t(x)=t+k2xw1<x<w2
t(x)=2x>w2
所述流場函數為,
u(x)=2x<w1
u(x)=uc+k1xw1<x<w2
u(x)=4x>w2。
優選地,還包括:
二維仿真模塊,用於在sar對海面的觀測角在20°-70°,風向為100°時,根據基於上升流的海表溫度函數和流場函數,對高頻微尺度波的波譜解進行海洋鋒面仿真,得到二維sar海面仿真。
有益效果如下:
本申請實施例所提供的sar海面仿真方法及裝置,根據海表粗糙度,利用雷達成像模型得到海表高頻微尺度波的波譜,根據海表高頻微尺度波的波譜,利用能量控制方程得到高頻微尺度波的波譜解,基於上升流的海表溫度函數,對高頻微尺度波的波譜解進行海洋鋒面仿真,得到sar海面仿真,以解決現有存在的sar海面仿真結果準確性較差的技術問題,從而滿足人們對海面仿真有效性的需求。
附圖說明
下面將參照附圖描述本申請的具體實施例,其中:
圖1示出了本申請實施例一中sar海面仿真的方法原理圖;
圖2示出了本申請實施例一中sar海面仿真的方法流程圖;
圖3示出了本申請實施例一中sar海面仿真的雷達成像模型原理假設示意圖;
圖4示出了本申請實施例二中sar海面仿真的sst變化分布示意圖;
圖5示出了本申請實施例二中sar海面仿真的sst引起的nrcs變化仿真結果示意圖;
圖6示出了本申請實施例二中sar海面仿真的流場及sst變化分布示意圖;
圖7示出了本申請實施例二中sar海面仿真的流場及sst變化引起的上升流一維仿真結果示意圖;
圖8示出了本申請實施例二中sar海面仿真的流場及sst變化引起的上升流二維仿真結果示意圖;
圖9示出了本申請實施例三中sar海面仿真的裝置結構圖。
具體實施方式
為了使本申請的技術方案及優點更加清楚明白,以下結合附圖對本申請的示例性實施例進行進一步詳細的說明,顯然,所描述的實施例僅是本申請的一部分實施例,而不是所有實施例的窮舉。並且在不衝突的情況下,本說明中的實施例及實施例中的特徵可以互相結合。
在上升流的形成過程中,海水由深層向海表淺層運動,海表溫度(sst:seasurfacetemperature)會隨該過程形成一個溫度變化,海表流場也會發生變化,伴隨劇烈的海氣運動,物理參數以及相應的化學生物參數也會發生變化,其中溫度變化和海表流場改變是上升流的形成過程中兩個比較重要的影響方面。
sar利用散射信號的都卜勒頻移獲得相對較高的方位解析度,同時通過發射微波脈衝得到較高的距離解析度,並通過搭載在飛機或者衛星上以實現對海表面的高精度監測。根據布拉格散射機制,在中等入射角情況下,也就是當星載sar對海洋的觀測角範圍為20°~70°時,一般採用bragg共振散射理論,bragg共振散射是指將粗糙海表面看作許多平面波線性疊加。此外,電磁波散射也是一個線性過程,在遠離海表面的情形下,粗糙海表面各不同波分量相干疊加,增強了一定尺度的周期性結構散射,同時,削弱其他周期性結構散射,如同衍射光柵一樣。同時,結合海表流場對sar成像的影響,採用雷達成像模型,進一步探究上升流的過程。
本申請利用sar接收到的信號依賴於表面應力和表面粗糙度的關係,結合海表面溫度對海表空氣密度、海水密度以及海水的粘性係數等的影響,通過sst來改變釐米尺度波的成長速度。具體地,將sst引入到雷達成像模型中,對上升流過程進行仿真,通過對上升流過程與海表粗糙度兩者之間的影響因素,分析波流相互作用,即海表流場對上升流的影響,再通過結合海表流場,分析海表流場對上升流過程中sar海浪成像的影響,以探究上升流在sar成像中的機理。
為了便於本申請的實施,下面以實例進行說明。
實施例一、
圖1示出了本申請實施例一中sar海面仿真的方法原理圖,如圖1所示,包括:
步驟101:根據海表粗糙度,利用雷達成像模型得到海表高頻微尺度波的波譜。
步驟102:根據海表高頻微尺度波的波譜,利用能量控制方程得到高頻微尺度波的波譜解。
步驟103:基於上升流的海表溫度函數,對高頻微尺度波的波譜解進行海洋鋒面仿真,得到sar海面仿真。
進一步地,所述根據海表粗糙度,利用雷達成像模型得到海表高頻微尺度波的波譜的步驟包括:
通過量化海表粗糙度,獲得雷達信號的歸一化後向散射截面強度,所述海表粗糙度包括大尺度波傾斜造成的均方斜率、波浪破碎,以及布拉格波;
歸一化後向散射截面強度的計算公式為,
其中,代表布拉格波散射,代表由均方斜率構成的雷達信號的鏡面反射,代表大尺度波的波浪破碎。
進一步地,所述根據海表高頻微尺度波的波譜,利用能量控制方程得到高頻微尺度波的波譜解的步驟包括:
高頻微尺度波的波譜具有能量平衡狀態,能量控制方程為,
高頻微尺度波的波譜解計算公式為,
進一步地,所述根據基於上升流的海表溫度函數,對高頻微尺度波的波譜解進行海洋鋒面仿真,得到sar海面仿真的步驟包括:
根據上升流的海表溫度函數,利用拖曳係數確定海表風摩擦速度;
根據海表風摩擦速度,計算出所述海表溫度函數對應的風應力值;
在sar對海面的觀測角在20°~70°時,根據所述風應力值,對高頻微尺度波的波譜解進行布拉格仿真,得到後向散射截面強度;
其中,海表溫度函數為,
t(x)=1x<w1
t(x)=t+k1xw1<xw2。
進一步地,所述對高頻微尺度波的波譜解進行布拉格仿真,得到後向散射截面強度的步驟包括:
當波長λb=λr/2sinθ時,該波長λb的微尺度波為布拉格波,利用布拉格共振散射機制計算後向散射截面強度,計算公式為,
其中,kr=2π/λr,kb=2π/λb分別為雷達波波數和布拉格波波數;gpp為極化函數,ψ為微尺度波波譜。
進一步地,還包括:
在sar對海面的觀測角在20°~70°時,根據基於上升流的海表溫度函數和流場函數,對高頻微尺度波的波譜解進行海洋鋒面仿真,得到一維sar海面仿真;
其中,海表溫度函數為,
t(x)=1x<w1
t(x)=t+k2xw1<x<w2
t(x)=2x>w2
所述流場函數為,
u(x)=2x<w1
u(x)=uc+k1xw1<x<w2
u(x)=4x>w2。
進一步地,還包括:
在sar對海面的觀測角在20°~70°,風向為100°時,根據基於上升流的海表溫度函數和流場函數,對高頻微尺度波的波譜解進行海洋鋒面仿真,得到二維sar海面仿真。
本申請基於sst和海表流場在上升流過程中的影響,利用雷達成像模型結合sar海面散射模型,分析上升流在sar成像中的機理,圖2示出了本申請實施例一中sar海面仿真的方法流程圖,如圖2所示,具體方法如下:
步驟201:利用雷達成像模型,分析海表波浪對雷達成像過程的影響。
圖3示出了本申請實施例一中sar海面仿真的雷達成像模型原理假設示意圖,如圖3所示,雷達成像模型是基於以下假設與原則進行的,影響海表粗糙度的主要因素包括海表流場分布,海表面附近風場以及海表面的活性物質,以上三者共同決定著海洋表面的粗糙度,將粗糙度分割成大尺度的波浪和小尺度的布拉格波。其中,在大尺度的波浪中,海面均方斜率主要構成對雷達信號的鏡面反射(sp),同時也通過短波的傾斜對布拉格波bragg(br)散射產生一定的影響,同時,大尺度波浪的波浪破碎(wb)也會改變海表的粗糙度並生成小尺度的布拉格波,以上因素均影響雷達的後向散射截面強度,可見,通過對上述參數的量化,能夠近似獲得雷達的後向散射截面強度。
海表粗糙度由大尺度波浪傾斜造成的均方斜率(mss)以及波浪破碎(wb)和小尺度bragg波(br)組成,以上三者構成歸一化雷達後向散射截面(nrcs:normalizedradar-backscattercrosssection):
其中,代表布拉格波散射,代表鏡面反射,代表波浪破碎,對雷達信號散射造成的影響。在雷達入射角範圍內,一般鏡面反射部分微弱,可以忽略;由于波浪破碎可以在局部地區形成一個較強的散射信號,對於h極化的雷達信號而言,雖然波浪破碎所佔的比重不多,但難以直接忽略;此外,釐米尺度的bragg波可以由長波(如,分米波或者更長)的波浪破碎生成得到,一般也難以直接忽略。
步驟202:根據能量控制方程,在波浪譜s(k)平衡範圍內,將上述假設簡化為以下方程:
其中,(2)式第一項表示風應力和粘性耗散,第二項表示非線性耗散,第三項表示由于波浪破碎造成的能量輸入。在(2)式中,風浪飽和譜α和n均是經驗參數,成長速度β是風的成長速度βw和粘性耗散βv兩者之差。粘性耗散βv由(3)式計算得到:
βv=4vk2/ω(3)
風的成長速度βw由(4)式計算得到:
其中,是風向與波浪方向的夾角,k是波數,u*是摩擦風速,uπ/k是在高處z=π/k時的風速,c=ω/k為相速度。波浪頻率ω=(gk+γk3)0.5,sst通過對海水表面張力γ的改變以影響波浪頻率ω。
釐米尺度的風浪在海表數釐米處通過海氣之間的相互作用生成,海表附近的海水溫度與空氣溫度較為接近,空氣溫度ta對於(4)式中的影響主要體現在ρa,而海水溫度tw對於(3)式中的影響集中於海水粘性係數v上。此外,摩擦風速u*可通過拖曳係數cd計算得到:
u*2=cdu2(5)
其中,u為海面風速,u*用於反映海氣之間的動量交換。拖曳係數cd採用風速w和大氣海洋溫差(ta-tw)的函數關係獲得,通過多項式近似表示如下,
cd=α1+α2u+α3(ta-tw)+α4u2+α5(ta-tw)2+α6u(ta-tw)(6)
具體的拖曳係數cd表達式如下:
cd=0.934×10-3+0.788×10-4u+0.868×10-4δt-0.616×10-6u2
-0.12×10-5δt2-0.214×10-5uδt(7)
其中,δt=ta-tw,單位為℃。
步驟203:在通過雷達成像模型獲得波譜後,將波譜解代入bragg仿真模型中。
步驟204:在海面上,不同尺度的周期性結構由不同波長的微尺度波組成,對于波長為kr,入射角為θ的雷達波,波峰線與雷達視線垂直的特定波長λb的微尺度波發生bragg共振散射。當波長λb=λr/2sinθ時,該波長λb的微尺度波即為bragg波,由bragg共振散射理論獲得的nrcs如下所示:
其中,kr=2π/λr,kb=2π/λb分別是雷達波波數和bragg波波數;gpp是極化函數,εr是海水復介電常數;下標hh和vv分別代表發生和接收信號的極化方式,ψ是二維微尺度波波譜。
實施例二、
圖4示出了本申請實施例二中sar海面仿真的sst變化分布示意圖;,如圖4所示,利用一維海洋鋒面仿真以驗證仿真模型的可行性,即採用一維sst進行仿真實驗,海水溫度、大氣溫度、風速均為定常條件,只有上升流引起的海水溫度為變量t(x),一維sst函數為:
t(x)=1x<w1
t(x)=t+k1xw1<xw2
圖5示出了本申請實施例二中sar海面仿真的sst引起的nrcs變化仿真結果示意圖,如圖5所示,通過仿真c-band條件下的鋒面情況,波數入射角採用中等入射角(θ=30°),將上述條件代入到仿真模型中,得到一維仿真結果為,鋒面與sst變化較為吻合,能夠反映出在上升流過程中,海表溫度對sar成像產生的影響。
基於上升流過程中sst形成的nrcs變化範圍,將sst影響因子和流場加入到控制方程中。一般認為,海面高頻微尺度波的波譜具有能量平衡狀態,能量控制方程如下:
其中,ψ(k)為微尺度波波譜,對應散射模型中的微尺度波波譜,cg為波群速度,方程左側代表微尺度波波譜隨時間的變化,右側對應各能量的輸入,具體包括:風輸入源函數sin(k),非線性波相互作用源函數snl(k),由於分子粘性作用和海浪破碎引起的耗散源函數sds(k),波流相互作用源函數scu(k),在海洋高頻波譜傳播中,各輸入平衡,則:
sin(k)+snl(k)+sds(k)+scu(k)=0(12)
各輸入源對應的表達式如下:風輸入源函數的譜形式:式中,m=0.04;毛細-重力波段的源函數:snl(k)=-m3k-4ωb2(k),和毛細波段的源函數:snl(k)=-m4k-4ωb2(k),式中m3和m4分別為無量綱常數;分子粘性力耗散源函數:sds(k)=-4γk2ψ(k),加入耗散源函數得到:sbk(k)=-36ωk10ψ(k)3.5;由于波流相互作用源函數理論解過於複雜,採用0階近似數值形式:
其中,u和v為大尺度背景流場(流,海洋鋒,內波,地形)的速度分量,為微尺度波的傳播波向,即為由於海面風誘發的微尺度波的傳播方向,認為與風向平行。
結合上述分析,在c波段發生共振的海表微尺度波的波譜解形式如下,
加入sst影響因子進行分析,sst通過影響拖曳係數,改變海面風摩擦速度的大小,結合(5)式,對海溫tw進行求導,獲得sst對應的風應力影響因子:1/2d(lncd)/d(tw),將影響因子代入波譜解,並僅考慮c波段vv極化中等入射角條件下的仿真,可得:
圖6示出了本申請實施例二中sar海面仿真的流場及sst變化分布示意圖,如圖6所示,採用一維流場與sst進行仿真實驗,假定大氣溫度、海表面溫度和風速均為定常(u=15m/s,ta=5℃,tw=15℃),變量只有流場u(x),v(x)與流場伴生的海面水溫異常t(x)。一維流場函數為:
u(x)=2x<w1
u(x)=uc+k1xw1<x<w2
u(x)=4x>w2
同樣的,一維sst函數為:
t(x)=1x<w1
t(x)=t+k2xw1<x<w2
t(x)=2x>w2
圖7示出了本申請實施例二中sar海面仿真的流場及sst變化引起的上升流一維仿真結果示意圖,如圖7所示,通過仿真c-band條件下的鋒面狀況,即考慮bragg仿真模型的使用範圍,並採用典型的中等入射角(θ=30°)代入海洋鋒面的仿真模型,得到一維仿真結果為,鋒面與流速梯度吻合性較好,能夠得到明顯的鋒面邊緣與鋒面內部的變化趨勢。
圖8示出了本申請實施例二中sar海面仿真的流場及sst變化引起的上升流二維仿真結果示意圖,如圖8所示,採用海洋鋒仿真模型對二維海面仿真,假定條件(風向=100°,入射角θ=30°),二維海洋鋒面仿真結果為,nrcs整體由風速控制,即nrcs的總體變化趨勢由風速梯度控制,流速梯度控制nrcs的局部變化趨勢。
基於同一發明構思,本申請實施例中還提供了一種sar海面仿真裝置,由於這些設備解決問題的原理與一種sar海面仿真方法相似,因此這些設備的實施可以參見方法的實施,重複之處不再贅述。
實施例三、
圖9示出了本申請實施例三中sar海面仿真的裝置結構圖,如圖9所示,裝置可以包括:
波譜模塊901,用於根據海表粗糙度,利用雷達成像模型得到海表高頻微尺度波的波譜。
波譜解模塊902,用於根據海表高頻微尺度波的波譜,利用能量控制方程得到高頻微尺度波的波譜解。
仿真模塊903,用於基於上升流的海表溫度函數,對高頻微尺度波的波譜解進行海洋鋒面仿真,得到sar海面仿真。
進一步地,所述波譜模塊901包括:
通過量化海表粗糙度,獲得雷達信號的歸一化後向散射截面強度,所述海表粗糙度包括大尺度波傾斜造成的均方斜率、波浪破碎,以及布拉格波;
歸一化後向散射截面強度的計算公式為,
其中,代表布拉格波散射,代表由均方斜率構成的雷達信號的鏡面反射,代表大尺度波的波浪破碎。
進一步地,所述波譜解模塊902包括:
高頻微尺度波的波譜具有能量平衡狀態,能量控制方程為,
高頻微尺度波的波譜解計算公式為,
進一步地,所述仿真模塊903包括:
根據上升流的海表溫度函數,利用拖曳係數確定海表風摩擦速度;
根據海表風摩擦速度,計算出所述海表溫度函數對應的風應力值;
在sar對海面的觀測角在20°~70°時,根據所述風應力值,對高頻微尺度波的波譜解進行布拉格仿真,得到後向散射截面強度;
其中,海表溫度函數為,
t(x)=1x<w1
t(x)=t+k1xw1<xw2。
進一步地,,所述對高頻微尺度波的波譜解進行布拉格仿真,得到後向散射截面強度的步驟包括:
當波長λb=λr/2sinθ時,該波長λb的微尺度波為布拉格波,利用布拉格共振散射機制計算後向散射截面強度,計算公式為,
其中,kr=2π/λr,kb=2π/λb分別為雷達波波數和布拉格波波數;gpp為極化函數,ψ為微尺度波波譜。
進一步地,還包括:
一維仿真模塊904,用於在sar對海面的觀測角在20°~70°時,根據基於上升流的海表溫度函數和流場函數,對高頻微尺度波的波譜解進行海洋鋒面仿真,得到一維sar海面仿真;
其中,海表溫度函數為,
t(x)=1x<w1
t(x)=t+k2xw1<x<w2
t(x)=2x>w2
所述流場函數為,
u(x)=2x<w1
u(x)=uc+k1xw1<x<w2
u(x)=4x>w2。
進一步地,還包括:
二維仿真模塊905,用於在sar對海面的觀測角在20°~70°,風向為100°時,根據基於上升流的海表溫度函數和流場函數,對高頻微尺度波的波譜解進行海洋鋒面仿真,得到二維sar海面仿真。
上述實施例中,均可以採用現有的功能元器件模塊來實施。例如,處理模塊可以採用現有的數據處理元器件,至少,現有定位技術中採用的定位伺服器上便具備實現該功能元器件;至於接收模塊,則是任意一個具備信號傳輸功能的設備都具備的元器件;同時,處理模塊進行的a、n參數計算、強度調整等採用的都是現有的技術手段,本領域技術人員經過相應的設計開發即可實現。
為了描述的方便,以上所述裝置的各部分以功能分為各種模塊或單元分別描述。當然,在實施本申請時可以把各模塊或單元的功能在同一個或多個軟體或硬體中實現。
本領域內的技術人員應明白,本申請的實施例可提供為方法、系統、或電腦程式產品。因此,本申請可採用完全硬體實施例、完全軟體實施例、或結合軟體和硬體方面的實施例的形式。而且,本申請可採用在一個或多個其中包含有計算機可用程序代碼的計算機可用存儲介質(包括但不限於磁碟存儲器、cd-rom、光學存儲器等)上實施的電腦程式產品的形式。
本申請是參照根據本申請實施例的方法、設備(系統)、和電腦程式產品的流程圖和/或方框圖來描述的。應理解可由電腦程式指令實現流程圖和/或方框圖中的每一流程和/或方框、以及流程圖和/或方框圖中的流程和/或方框的結合。可提供這些電腦程式指令到通用計算機、專用計算機、嵌入式處理機或其他可編程數據處理設備的處理器以產生一個機器,使得通過計算機或其他可編程數據處理設備的處理器執行的指令產生用於實現在流程圖一個流程或多個流程和/或方框圖一個方框或多個方框中指定的功能的裝置。
這些電腦程式指令也可存儲在能引導計算機或其他可編程數據處理設備以特定方式工作的計算機可讀存儲器中,使得存儲在該計算機可讀存儲器中的指令產生包括指令裝置的製造品,該指令裝置實現在流程圖一個流程或多個流程和/或方框圖一個方框或多個方框中指定的功能。
這些電腦程式指令也可裝載到計算機或其他可編程數據處理設備上,使得在計算機或其他可編程設備上執行一系列操作步驟以產生計算機實現的處理,從而在計算機或其他可編程設備上執行的指令提供用於實現在流程圖一個流程或多個流程和/或方框圖一個方框或多個方框中指定的功能的步驟。
儘管已描述了本申請的優選實施例,但本領域內的技術人員一旦得知了基本創造性概念,則可對這些實施例作出另外的變更和修改。所以,所附權利要求意欲解釋為包括優選實施例以及落入本申請範圍的所有變更和修改。
