一種基於玉米粒碰撞聲信號多域融合的PSO‑SVM優化方法與流程

2023-04-24 12:51:46 1

本發明屬於碰撞聲檢測領域，具體涉及一種基於玉米粒碰撞聲信號多域融合的pso-svm優化方法。

背景技術：

糧食作為人類生存的必需品，人類的生活處處離不開糧食。但糧食產後損失是一個世界性難題，根據統計調查，糧食產後損失率在發達國家一般為3％，在發展中國家一般為5％，我國糧食產後損失率達到8％。每年產後糧食損失量為500億斤，這相當於1億多畝地生產的糧食被浪費。糧食產後損失中，儲存環節損失所佔比重最高，損失比例達到40.3％。這是由於糧食儲存環節，極易受到蟲害和黴菌的危害。這些危害不但會降低糧食的產量，而且也會降低糧食的質量。人類長期食用這類糧食，不但會出現營養不良，甚至會導致誘發各種疾病。在農產品中，由於玉米自身的特性更易受到蟲類和黴菌的危害。玉米的胚佔整個玉米顆粒體積的1/3左右，佔重量的10％～20％。玉米的胚含有較多的蛋白質和大量可溶性糖，由於胚部營養成分較多，容易被微生物寄生和遭到蟲類危害，導致玉米的帶菌量遠大於其他禾穀類糧食。因此，在玉米的儲藏過程中預防蟲害和黴菌感染的檢測工作具有重要的現實意義。

傳統的儲糧檢測方法常見有二氧化碳檢測、x射線成像法、尿酸檢測、機器視覺法等，這些方法有一定的優勢，但也存在局限性。目前，利用碰撞聲進行檢測的方法因其效率高和方便等諸優勢已經引起有關研究人員的注意。

技術實現要素：

針對現有技術中的不足，本發明提出一種基於玉米粒碰撞聲信號多域融合的pso-svm優化方法，目的在於通過提取玉米粒碰撞聲信號時域特徵、頻域特徵和希爾伯特域特徵，且將所述特徵送入到粒子群優化的支持向量機進行識別和檢測，以提高玉米完好粒、蟲蛀粒和黴變粒的識別率。

一種基於玉米粒碰撞聲信號多域融合的pso-svm優化方法，具體包括：

s1：對玉米粒碰撞聲信號進行eemd分解；

s2：提取玉米粒碰撞聲信號的時域特徵；

所述步驟s2包括：

s21：計算平均振幅變化，所述平均振幅變化用於代表信號衰減，計算公式為：

s22：統計wilson振幅值，當碰撞聲信號振幅的變化超過給定閾值時，所述wilson振幅的值就加1，否則不變，計算公式為：

s23：計算峰峰值，所述峰峰值為在信號的時間序列中最大值和最小值之間的差異，用於描述信號幅值總體的變化範圍，計算公式為：

pk-pk＝max(ci，k)-min(ci，k)；

s24：計算樣本熵，所述樣本熵的計算公式為：

當n為有限值時，計算公式為：

以上各式中，n是信號採樣點數，ci，k為第k次試驗的第i階imf分量；

s3：提取玉米粒碰撞聲信號的頻域特徵；

所述步驟s3包括：

s31：計算頻率均值，對原始碰撞聲信號做fft變換，提取fft變換幅度均值作為所述頻率均值，計算公式為：

其中，m代表採樣點個數，x(k)表示經傅立葉變換之後的幅度；

s32：計算功率譜均方根，所述功率譜均方根用於反映功率譜能量的離散程度，計算公式為：

其中，m代表採樣點個數，p代表功率譜的幅度；

s33：計算頻帶方差，所述頻帶方差用於表示信號在不同頻帶的能量方差，計算公式為：

其中，m代表採樣點個數，x(k)表示經fft變換之後的幅度；

s4：提取玉米粒碰撞聲信號的希爾伯特域特徵；

所述步驟s4包括：

s41：計算低頻帶能量和高頻帶能量，所述高頻帶頻率範圍為10～15khz，計算公式為：

所述低頻帶頻率範圍為5～10khz，計算公式為：

ah，i為高頻帶瞬時強度，al，i為低頻帶瞬時強度，n為信號採樣點數；

s42：計算包絡平均值，具體步驟又包括：

s421：對前幾個imf做hilbert變換定義為：

其中，h[]為hilbert變換；

s422：分別以c(i)和hilbert變換h(ci(t))為實部和虛部，由此可以將原始信號解析表示如下：

z(t)＝c(i)+jh[ci(t)]；

s423：信號的包絡b(t)就是上述解析信號的幅值函數：

s424：包絡譜則可以由對包絡函數b(t)進行傅立葉變換求出：

a(f)＝f(b(t))；

s5：利用pso算法優化svm參數，構建pso-svm分類器，用於對所提取的玉米粒碰撞聲信號的時域特徵、頻域特徵和希爾伯特域特徵進行分類識別，以獲得更高的玉米顆粒完好粒、黴變粒和蟲蛀粒的識別率；

所述步驟s5包括：

s51：初始化粒子群，隨機產生粒子的位置和速度；

s52：利用碰撞聲信號樣本，訓練svm分類器並計算適應度值，採用交叉驗

證的方法計算適應度值；

s53：根據適應度值更新個體極值和全局最優值；

s54：更新當前粒子的速度和位置；

s55：當達到迭代次數或滿足適應度條件時，則終止迭代；否則返回步驟s52。

發明效果：

根據本發明具有如下效果：多域融合可以提高碰撞聲信號的特徵分類效果，有助於識別玉米完好粒，黴變粒和蟲蛀粒。

附圖說明

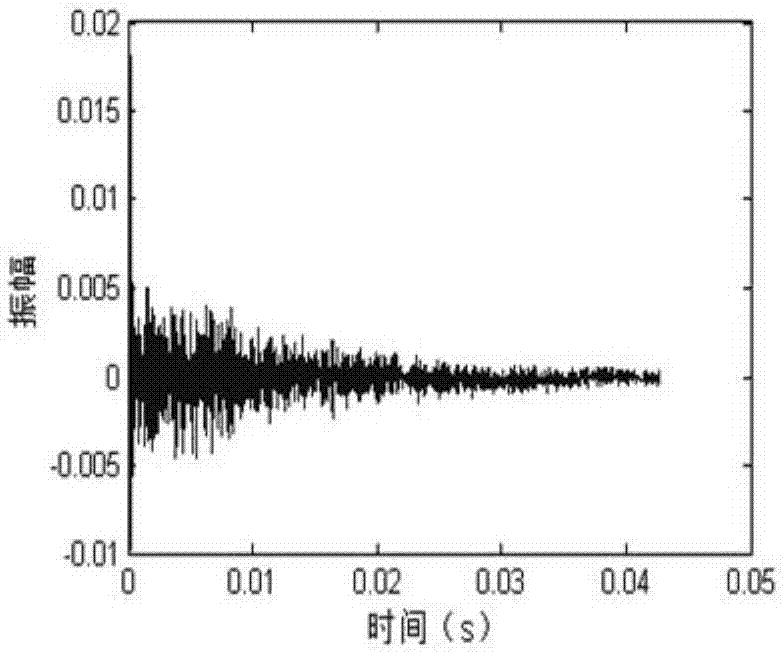
圖1(a)-圖1(c)是本發明實施例提供的玉米完好粒、蟲蛀粒和黴變粒三類碰撞聲信號時域圖；

其中，圖1(a)為完好粒，圖1(b)為蟲蛀粒，圖1(c)為黴變粒；

圖2(a)-圖2(d)是本發明實施例提供的三類玉米粒碰撞聲信號的平均振幅變化散點圖；

其中，圖2(a)為imf1的平均振幅變化散點圖，圖2(b)為imf2的平均振幅變化散點圖，圖2(c)為imf3的平均振幅變化散點圖，圖2(d)為imf4的平均振幅變化散點圖；

圖3是本發明實施例提供的三類碰撞聲信號的wilson振幅均值圖；

圖4是本發明實施例提供的三類碰撞聲信號的峰峰值的均值圖；

圖5是本發明實施例提供的三類碰撞聲信號的樣本熵總數柱狀圖；

圖6(a)-圖6(c)是本發明實施例提供的玉米完好粒、蟲蛀粒和黴變粒三類碰撞聲信號的頻域圖；

其中，圖6(a)為完好粒，圖6(b)為蟲蛀粒，圖6(c)為黴變粒；

圖7是本發明實施例提供的三類碰撞聲信號的頻率均值圖；

圖8是本發明實施例提供的三類碰撞聲信號的功率譜均方根幅值圖；

圖9是本發明實施例提供的三類碰撞聲信號的頻帶方差圖；

圖10是本發明實施例提供的三類碰撞聲信號的包絡平均值對比圖；

圖11是本發明實施例提供的pso優化svm參數的流程圖；

圖12是本發明實施例提供的基於多域融合的玉米受損顆粒檢測系統流程圖；

圖13是本發明實施例提供的pso適應度曲線圖。

具體實施方式

下面結合附圖和實施例對本發明作進一步的詳細描述。

本發明的基本思想在於提取玉米粒碰撞聲信號的時域特徵、頻域特徵和希爾伯特域特徵，利用pso優化svm分類器，對上述多域特徵進行分類識別。

本發明實施例提供一種基於玉米粒碰撞聲信號多域融合的pso-svm優化方法，具體技術方案如下：

1、對玉米粒碰撞聲信號進行eemd分解

eemd又稱總體經驗模態分解，該方法是將白噪聲添加到原始信號中作為一個新的信號序列，對此信號序列進行emd得到imf，通過多次添加白噪聲獲取imf，然後對所得imf進行平均處理，經過多次平均運算之後，加入原始信號的白噪聲可以相互抵消。

2.提取玉米粒碰撞聲信號時域特徵

如圖1(a)-圖1(c)所示的時域圖中，我們看出玉米完好粒、蟲蛀粒和黴變粒三種類型的碰撞聲信號的幅值的波動範圍不同，各類信號的衰減程度有區別。提取四個時域特徵，即平均振幅變化(aac)、wilson振幅(wamp)、峰峰值(pk-pk)、樣本熵。

2.1計算平均振幅變化(aac)

由時域圖可以看出，玉米完好粒、蟲蛀粒和黴變粒三類碰撞聲信號的衰減程度有差別。用振幅變化代表信號的衰減，計算公式如下：

其中，n取值2048。

圖2(a)-圖2(d)展示了三類玉米粒碰撞聲信號的平均振幅變化散點圖，星號代表的是完好粒，五角星代表的是黴變粒，圓圈代表的是蟲蛀粒，圖2(a)、圖2(b)、圖2(c)、圖2(d)分別代表了imf1、imf2、imf3、imf4的平均振幅變化散點圖，其中，imf1、imf2、imf3、imf4分別為eemd在第1階、第2階、第3階、第4階的固有模態函數。從圖中可以看出，imf1和imf2中，除了有少部分相互重疊，三類碰撞聲信號具有良好的可分性，但在imf3、imf4中，使用此特徵的重疊部分相對比較多，特別是imf4的平均振幅改變的散點圖相互混淆，無法區分三類碰撞聲信號。

2.2統計wilson振幅值(wamp)

wilson振幅是指碰撞聲信號中相鄰兩個時間段之間的振幅差異超過了預定義閾值的數目。當碰撞聲信號振幅的變化超過給定閾值時，wilson振幅的值就加1，否則不變，計算公式如下：

其中，n取值2048。

對於每一個imf分量，圖3分別展示三類碰撞聲信號的wilson振幅均值圖的變化情況。從均值圖中可以看出，三類碰撞聲的wilson振幅的變化趨勢是相似的，對於第1階imf分量，完好粒的wilson振幅平均值大於蟲蛀粒和黴變粒的wilson振幅平均值，但是由於三種碰撞聲信號wilson振幅平均值曲線的趨勢相似，在第3階imf分量之後，完好粒、蟲蛀粒和黴變粒碰撞聲信號的wilson振幅均值就相互重疊，所以本實施例提取前三階imf分量的wilson振幅作為判別特徵向量。

2.3計算峰峰值(pk-pk)

峰峰值是指在信號的時間序列中最大值和最小值之間的差異，即最大值和最小值之間的範圍。峰峰值描述了信號幅值總體的變化範圍，計算公式如下：

pk-pk＝max(ci，k)-min(ci，k)(3)

對於每一階imf，圖4展示了三類碰撞聲信號的峰峰值的均值圖變化趨勢。在前4階imf分量之前，完好粒碰撞聲信號的峰峰值的均值大於其他兩種碰撞聲信號的峰峰值的均值，三類信號的峰峰值曲線相互不交叉，說明峰峰值可以用來區分三類信號。

2.4計算樣本熵

對於每一個具有n個採樣點的時間序列{x(n)＝x(1)，x(2)，…，x(n)}，樣本熵可以定義為如下：

①按照序號形成一組大小為m的向量序號，xm(1)，…xm(n-m+1)，其中xm(i)＝{x(i)，x(i+1)，…，x(i+m-1)}，1≤i≤n-m+1，這些向量表示從i點開始的選取m個連續的x值。

②d[xm(i)，xm(j)]是向量xm(i)與xm(j)之間最大差值的絕對值，即兩者之間的最大距離：

d[xm(i)，xm(j)]＝maxk＝0，1，…，m-1(|x(i+k)-x(j+k)|)(4)

③給定一個xm(i)，統計xm(i)與xm(j)之間距離小於或等於r的j(1≤j≤n-m，j≠i)的數目，並記為bi。對於1≤i≤n-m，定義：

④定義b(m)(r)為：

⑤增加數組的維數到m+1，計算xm+1(i)與xm+1(j)(1≤j≤n-m，j≠i)距離小於等於r的個數，記為ai。定義為：

⑥定義am(r)為：

這樣，bm(r)是兩個序列在相似容限r下匹配m個點的概率，而am(r)是兩個序列匹配m+1個點的概率。樣本熵定義為：

當n為有限值時，可以用下式估計：

圖5是對每一類碰撞聲信號的樣本熵進行求和所得總值的柱狀圖。從圖中可以看到，在第1階imf時，三種碰撞聲信號的樣本熵有較大的不同。隨著imf階數的增加，玉米蟲蛀粒碰撞聲信號的樣本熵總數下降比較快，而玉米黴變粒碰撞聲信號的樣本熵總數下降比較慢，差別逐漸減小。這是因為信號經過eemd分解之後，前幾階imf包含了信號的主要信息。在本發明實施例中，取m＝2，r＝0.25std(std代表原始數據的標準差)，n＝2048。

3.提取玉米粒碰撞聲信號頻域特徵

圖6(a)-圖6(c)為玉米完好粒、蟲蛀粒和黴變粒三類碰撞聲信號的頻域圖。從圖中可以看出，就整體趨勢而言，黴變粒有別於完好粒和蟲蛀粒，頻域最大幅值也有較大的差異，特別是黴變粒碰撞聲信號與其餘兩類玉米碰撞聲信號相比，其最大幅值偏低，較大幅值集中區域在較低頻率處，這與玉米粒被黴菌感染有關。

3.1計算頻率均值

對原始碰撞聲信號做fft變換，提取fft變換幅度均值作為特徵值，計算公式如下：

其中，m代表採樣點個數，取值2048。x(k)表示經傅立葉變換之後的幅度。

三類碰撞聲信號的頻率均值對比，如圖7所示。將三類碰撞聲信號按照以上公式求取碰撞聲信號的頻率均值，可以看出：黴變粒碰撞聲信號的頻率均值低於完好粒和蟲蛀粒，完好粒的頻率均值最高，此特徵可以用於識別受損顆粒。

3.2計算功率譜均方根(rmsps)

提取功率譜的均方根作為特徵向量，以反映功率譜能量的離散程度，計算公式如下：

其中，m代表採樣點個數，取值2048，p代表功率譜的幅度。

如圖8所示，三類碰撞聲信號的功率譜均方根幅值波動區域有差別。三條曲線互不混淆，說明此特徵向量可以檢測和識別受損的玉米顆粒(蟲蛀粒，黴變粒)。

3.3計算頻帶方差(fbv)

頻帶方差表示信號在不同頻帶的能量方差，物理意義是各頻帶間的波動特性和其短時能量特性。

其中，m代表採樣點個數，取值2048，x(k)表示經fft變換之後的幅度。

三類碰撞聲信號的頻帶方差對比，如圖9所示。由圖中可以看出，黴變粒的頻帶方差低於完好粒和蟲蛀粒的頻帶方差，完好粒碰撞聲信號的頻帶方差最高。這是因為玉米內部被蟲啃食之後，質量變輕，導致蟲蛀粒碰撞聲信號的頻帶方差低於完好粒碰撞聲信號的頻帶方差。黴變粒雖然內部並沒有被啃食，但因其表面受到黴菌感染，導致其內部結構發生變化，因而和完好粒碰撞聲信號有區別。

4.提取玉米粒碰撞聲信號希爾伯特域特徵

4.1計算低頻帶能量和高頻帶能量

將原始碰撞聲信號經過hilbert變換之後得到hh譜，在5～15khz頻率範圍內，三類信號有差別，將此頻段分為兩個部分，即定義5～10khz為低頻帶，定義10～15khz為高頻帶。根據帕斯維爾定理，信號x(t)的總能量為：

其中，xk表示信號第k個採樣點的幅值。

假設10～15khz為高頻帶瞬時強度為ah，i，5～10khz為低頻帶瞬時強度為al，i，高頻帶和低頻帶總能量分別為enh和enl：

其中，n取值2048。

三類信號的高頻帶能量和低頻帶能量的平均值、標準差如表1所示：

表1三類信號的高頻帶能量和低頻帶能量的平均值、標準差

由上表分析可知，完好粒的高、低頻帶能量均大於蟲蛀粒和黴變粒，這是由於蟲蛀粒和黴變粒受到損害，內部結構發生變化。

4.2計算包絡平均值(ave)

信號的包絡通常含有豐富信息，hilbert變換是求取信號包絡的主要方法之一。先對信號進行eemd分解，然後求取信號的包絡，具體步驟如下：

(1)對前幾個imf做hilbert變換定義為：

其中，h[]為hilbert變換；

(2)分別以c(i)和hilbert變換h(ci(t))為實部和虛部，由此可以將原始信號解析表示如下：

z(t)＝c(i)+jh[ci(t)](18)

(3)信號的包絡b(t)就是上述解析信號的幅值函數：

(4)包絡譜則可以由對包絡函數b(t)進行傅立葉變換求出：

a(f)＝f(b(t))

如圖10所示，是三類碰撞聲信號的包絡平均值對比圖。可以看出，完好粒碰撞聲信號包絡平均值波動比較大，而黴變粒碰撞聲信號包絡平均值的波動比較小，三類碰撞聲信號的包絡平均值波動的區域不同，相互之間並不混淆。

5.pso-svm分類器構建

5.1svm參數選擇

svm(supportvectormachine)又稱支持向量機，是一類新型機器學習方法，具有很好的學習性能。線性svm的原理是找到一個分類超平面作為決策曲面，最大化正例和反例的隔離邊緣。先考慮分兩類的情況，我們假設測試集數據是n維向量形成d維特徵空間x。對每一個向量xi，與之相關聯的目標函數yi∈{-1，+1}。在非線性情況下，通常將兩類用核方法投影到高維空間，使得原空間中的非線性問題轉化為新空間中的線性問題，它的決策規則是基於功能函數sign[f(x)]，其中f(x)代表在超平面中的判定函數，被定義如下：

f(x)＝ω*φ(x)+b*(20)

定義最優超平面中的權向量和偏差是一個最小化代價函數，它表示為如下兩個標準：利潤最大化和誤差最小化。

代價功能最小化有如下約束：

yi(ωφ(xi)+b)≥1-ξi，i＝1，2，…，n，ξi≥0，i＝1，2，…，n

其中，ξi表示的是不可分數據的鬆弛變量，常數c代表誤差項的懲罰因子。求解svm中的超平面問題可以通過建立拉格朗日函數將最初求解問題轉換為求解如下最優問題：

有如下約束：

其中，α＝[α1，α2，…，αn]是拉格朗日函數的向量，k(xi，xj)是核函數，計算公式如下：

k(xi，xj)＝exp(-g||xi-xj||2)，g>0(24)

核函數類型確定之後，求解最優問題還需要確定兩個未知數，即式(23)中的懲罰參數c及式(24)中核函數參數g，兩者的選取對於分類器的性能很重要。本文採用pso來選擇懲罰參數c以及核函數參數g，以提高支持向量分類器的分類效果。

5.2利用pso算法優化svm參數

所謂pso(particleswarmoptimization)，又稱粒子群優化算法或鳥群覓食算法，是一種隨機優化技術。設pso是在一個n維空間進行搜索目標，群落中共有m個粒子構成，定義x＝(x1，x2，…，xm)，那麼如果將i個粒子用n維向量表示，則可以表示為xi＝(xi1，xi2，…xin)t，第i個粒子飛行的速度表示為vi＝(vi1，vi2，…vin)t，pi＝(pi1，pi2…，pin)t代表第i個粒子迄今為止搜索到的最佳位置，也稱個體極值。整個粒子群搜索到的最佳位置為pb＝(pb1，pb2，…，pbn)t，也稱全局最優。在迭代過程中，粒子在搜索空間內單位迭代次數是由vi決定，粒子按照式(25)和式(26)更新自身的速度和位置，計算公式如下：

其中，rand1和rand2為屬於[0，1]的隨機分布函數，c1、c2為學習因子，相對於局部最優和全局最優調整相對速度。進一步地說，這些參數被認為是相對於局部最佳位置和全局最佳位置的比例因子，它們決定粒子的最佳位置。ω為慣性權值，ω∈[0.8，1.2]，實驗中ω的調整公式為：

ω＝ωmax-iter*(ωmax-ωmin)/itermax(27)

其中，iter為當前迭代次數，itermax為最大迭代次數。

本實施例利用pso算法對svm參數進行優化，用兩個粒子分別代表式(23)中的懲罰參數c及式(24)中核函數參數g來優化，如圖11所示，具體步驟如下：

(1)初始化粒子群，隨機產生粒子的位置和速度；

(2)利用碰撞聲信號樣本，訓練svm分類器並計算適應度值，採用交叉驗證的方法計算適應度值；

(3)根據適應度值更新個體極值和全局最優值；

(4)更新當前粒子的速度和位置；

(5)當達到迭代次數或滿足適應度條件時，則終止迭代；否則返回步驟(2)。

本實施例利用pso算法優化svm參數，構建pso-svm分類器，目的在於對所提取的玉米粒碰撞聲信號的時域特徵、頻域特徵和希爾伯特域特徵進行分類識別，以期獲得更高的玉米完好粒、黴變粒和蟲蛀粒識別率。

6.結果分析

6.1實驗檢測流程

本實施例展示了基於多域融合的玉米受損顆粒檢測系統流程，如圖12所示。對信號進行eemd分解，本文中加入白噪聲的幅值係數為0.2，總體平均次數為100，計算得到每一階imf。分別從時域、頻域和希爾伯特域提取可區分信號的特徵，隨後將這些特徵輸入到pso-svm進行檢測識別。本實施例共採用玉米碰撞聲信號840個，其中包括280個完好粒、280黴變粒和280個蟲蛀粒。從每類碰撞聲信號中隨機抽取140個，共420作為訓練集，剩下的玉米碰撞聲信號作為測試集，數據集的詳細說明見表2。

表2訓練集和測試集

6.2基於時域結果分析

通過前面的分析，時域特徵提取前3個平均振幅變化、前3個威爾遜振幅、前4個峰峰值、前2個樣本熵作為判別特徵。為了全面分析所提特徵的有效性，表3展示了特徵子集多種組合的識別率，目的是為了找到最優的組合。從表中可以看出，採用單個特徵時，黴變粒的識別率相對比較低，最高識別率達到85.7％。隨著組合的特徵數目增加，可看出黴變粒識別率在增加，即當使用全部的12個特徵作為判別特徵時，完好粒、蟲蛀粒和黴變粒的識別率分別達到97.1％、95.7％、93.6％，由此可知，提取的時域特徵能夠檢測出受損玉米顆粒。

表3時域不同特徵子集下檢測識別率

6.3基於頻域結果分析

表4給出了頻域特徵子集下的檢測識別率，可以看出，隨著特徵數目的增加，識別率不斷提高，當使用頻域全部特徵時，完好粒、蟲蛀粒和黴變粒的識別率分別可以達到98.6％、98.6％、97.8％。

表4頻域不同特徵子集下檢測識別率

6.4基於希爾伯特域結果分析

表5描述了當使用希爾伯特特徵時，各個特徵子集的檢測識別率。單獨使用一類特徵時，黴變粒的識別率比較低，即對於黴變粒的可分性低於完好粒和蟲蛀粒。而隨著特徵數目的不斷增加，三類碰撞聲信號的可分性增強。

表5希爾伯特域不同特徵子集下檢測識別率

6.5基於多域結果分析

本實施例的分類方法使用pso-svm，採用pso算法來選擇svm中的徑向基核函數中的參數g和懲罰係數c，通過200次迭代，5折交叉驗證，最優粒子的適應度值變化如圖13所示。最佳適應度曲線表示的是最優粒子的適應度變化，平均適應度表示所有粒子適應度值的平均，根據最初設定的參數，最優粒子的適應度從初始化參數時呈上升趨勢，直到迭代次數到達一定數時，適應度值才呈平穩不變的狀態。獲得的參數c＝9.15、g＝0.01，將訓練後的pso-svm用於測試樣本的判別，分類結果如表6。

表6多域不同特徵子集下檢測識別率

表6展示了不同域特徵子集下的檢測識別率，通過將三個域的特徵作為pso-svm的輸入，得到完好粒、蟲蛀粒和黴變粒的識別率分別是98.6％、99.2％、99.3％。

從表中還可以看出，通過將時域、頻域和希爾波特域的特徵進行融合後送入到svm和pso-svm分類器中，通過比較兩者之間的識別率，得出pso優化svm可以提高各類識別率。pso優化svm的分類模型比單獨運用svm算法能更快地找到最佳參數，也避免了隨機設定svm參數的盲目性，獲得更高的分類識別率。