基於GammaTest和NSGA‑II的分布式光伏出力預測輸入變量降維方法與流程
2023-05-04 22:05:46 5
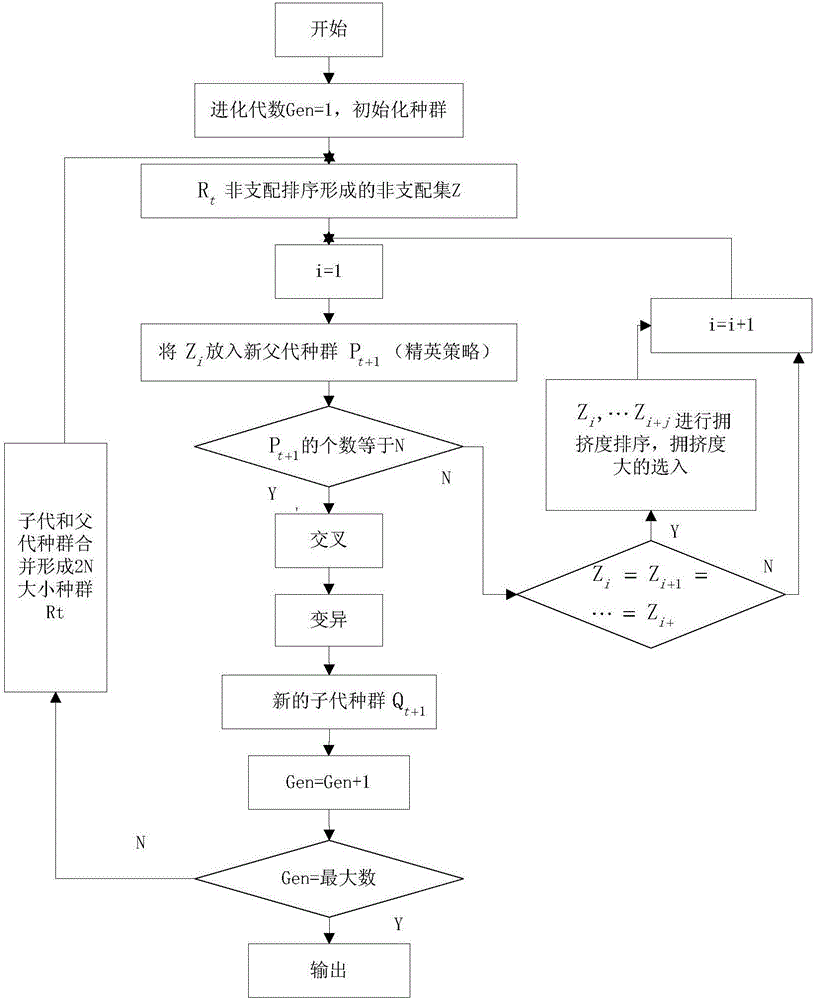
本發明屬於分布式光伏出力預測領域,特別是涉及一種基於Gamma Test和NSGA-II的分布式光伏出力預測輸入變量降維方法。
背景技術:
目前,光伏出力仍存在明顯的不連續性和不確定性。當分布式光伏系統併入公共電網時,光伏系統的擾動可能會影響電網的穩定性,這對電網的調度管理和用電安全產生了巨大的挑戰。為了消除這方面的影響,國內外對光伏發電系統的出力預測上做了大量研究。然而,光伏出力預測技術的實現還存在較多問題。
為了提高模型的預測精度,必須引入儘可能全面的輸入因子。但過多的輸入因子又會產生變量空間維度高、信息冗餘等問題,影響預測模型的精度。
因此,如何對預測系統的輸入變量進行降維,以提高預測模型的精度是亟需解決的問題。
技術實現要素:
為了克服已有光伏系統出力預測方式的輸入變量維度較高、預測精度較低的不足,本發明提供一種有效降低輸入變量維度、提升預測精度的基於Gamma Test和NSGA-II的分布式光伏出力預測輸入變量降維方法。
本發明解決其技術問題所採用的技術方案是:
一種基於Gamma Test和NSGA-II的分布式光伏出力預測輸入變量降維方法,所述降維方法包括以下步驟:
步驟1.原始輸入變量
分布式光伏出力預測的原始輸入變量包括歷史功率序列和氣象數據序列,所述歷史功率數據序列來自光伏電站電力參數檢測裝置,所述氣象數據序列來自光伏氣象站;
步驟2.數據預處理
對原始輸入變量進行數據預處理,首先對數據進行去噪處理,其次,對數據進行歸一化處理;
步驟3.構造新的變量因子
引入新的變量因子,包括組件溫度、小波分析數據以及晴空指數,所述組件溫度指光伏電池板表面的溫度,所述小波分析數據指採用小波分析法將光伏電站輸出功率分解為低頻分量和高頻分量,所述晴空指數指入射到水平面的實際輻射與晴空條件下的理論輻射之比;
步驟4.計算輸入變量的影響因子
以步驟2中經過預處理的數據和步驟3中引入的新變量作為輸入變量,首先採用Gamma Test對輸入變量的噪聲方差進行估計,其次,構造適應度函數,採用NSGA-II多目標遺傳算法對輸入變量的影響因子進行計算;
步驟5.構造降維後的輸入特徵向量。
根據步驟4中輸入變量的影響因子確定降維後的輸入變量,構造輸入特徵向量。
進一步,所述步驟4中,通過Gamma Test算法構造輸入變量的噪聲方差步驟如下:
首先,計算輸入空間中點xi與其第k個最鄰近點間距離的平均值為,
其中,k的範圍是1≤k≤kmax,xN[i,k]表示與xi最鄰近的向量,i的範圍是1≤i≤M;
其次,計算對應輸出數據之間的平均距離為,
其中,yN[i,k]是xi的第k個最鄰近點對應的輸出;
最後,構造線性方程為,
γM(k)=Γ+AδM(k)
其中Γ代表輸入變量的噪聲方差。
再進一步,所述步驟4中,構造適應度函數為,
其中,gΓ和gA是懲罰項,分別是Γ和A的函數,wΓ和wA是指定值,xi'為輸入向量。
更進一步,所述步驟5中,首先對影響因子為0的輸入變量進行剔除,其次,將影響因子為1的輸入變量組合,構造輸入特徵向量,實現輸入變量降維。
所述步驟1中,歷史功率序列包括直射輻射度、散射輻射度、水平總輻射度、傾斜面總輻射度以及輸出功率,氣象數據序列包括環境溫度、環境溼度、大氣壓、空氣可見度、風速、風向、天氣類型。
所述步驟2中,對原始輸入變量的去噪處理包含了數據填充和數據修正,採用線性插補法對缺失數據進行填充,採用相關性分析法對異常的氣象數據進行修正。
所述步驟2中,將每個輸入變量中的數據通過以下方法進行歸一化處理:
首先,將原始輸入變量表示為M={M1,M2,...,Mi},其次,將每個輸入變量下的樣本數據累加得生成累加數序列M'={M1',M2',...,Mk'},最後進行歸一化處理
上式中,i為輸入變量種類,M為樣本累加後的數值,Mmax為樣本累加後的最大值,Mmin為樣本累加後的最小值,Y為歸一化後的數值,Ymax為歸一化後的最小值,Ymin為歸一化後的最大值。
所述步驟3中,所述組件溫度為光伏面板表面溫度,組件溫度表達式為,T=Ta+kGt;其中Ta是環境溫度,k是經驗係數,Gt是t時刻傾斜面總輻射度。
所述步驟3中,引入小波分析數據是用小波分析法將光伏電站的輸出功率分解為低頻分量和高頻分量,即通過選擇合適的小波,重構各頻率分量,對重構後的高頻分量進行分類,從而可以針對不同天氣類型選擇合適的輸入變量。
所述步驟3中,所述晴空指數是指入射到水平面的實際輻射與晴空條件下的理論輻射之比,表達式為,
其中,Gt為入射到水平面的實際輻射度,入射到水平面的實際輻射。
本發明的有益效果主要表現在:
1、本發明實現了分布式光伏出力預測中輸入變量的降維,避免了過多的輸入因子產生的信息冗餘、建模複雜等問題,從而提高了光伏出力預測模型的精度。
2、該方法利用小波分析得到的高頻部分特徵值作為分類的依據,可以簡化模型,避免天氣預報不及時,天氣數據不完善造成的困擾。通過引入輻射度理論計算數據作為外生變量,降低對歷史數據中數據質量和數據環境的依賴。另外通過對相關因子二次計算,主要包括多時間尺度晴空指數,組件溫度修正數據和各小波分量。實現充分利用數據以及降低數據耦合程度的目的。
3、該方法能夠對不同天氣類型下的輸入變量進行分析,計算簡單,可用於短時尺度的光伏出力預測研究。
附圖說明
圖1為本發明的基於Gamma Test和NSGA-II的分布式光伏出力預測輸入變量降維方法流程圖。
圖2為本發明採用的NSGA-II算法流程圖。
圖3為本發明採用的光伏出力預測建模流程圖。
具體實施方式
下面結合附圖對本發明作進一步描述。
參照圖1~圖3,一種基於Gamma Test和NSGA-II的分布式光伏出力預測輸入變量降維方法,包括以下步驟:
步驟1,原始輸入變量
本實例選擇位於美國俄勒岡州的Ashland光伏發電系統(緯度:42.19°,經度:122.70°,海拔595m)作為算法研究對象,其總容量為15kW。預測的時間尺度是1小時,即預測分布式電站出力的小時平均功率。從光伏發電系統的電力參數檢測裝置記錄的歷史功率數據有:直射輻射度、散射輻射度、水平總輻射度、傾斜面總輻射度、輸出功率,從光伏氣象站記錄的氣象數據有:環境溫度、環境溼度、大氣壓、空氣可見度、風速、風向、天氣類型。
步驟2,數據預處理
對步驟1中的數據進行預處理,包括去噪處理和歸一化處理。
首先,對數據進行去噪處理。採用線性插補法對缺失數據進行填充,採用相關性分析法對異常的氣象數據進行修正。
其次,對原始輸入變量通過歸一化的方法將待處理的數據歸一化到[-1,1]區間。
步驟3,構造新的變量因子
引入新的變量因子,包括組件溫度、小波分析數據以及晴空指數。
首先,構造組件溫度。組件溫度為光伏面板表面溫度,組件溫度表達式為,
T=Ta+kGt
其中,Ta是環境溫度,k是經驗係數,Gt是t時刻傾斜面總輻射度。
其次,構造小波分析數據。以步驟2中經過預處理的光伏電站輸出功率為輸入,採用小波分析法進行三層分解,分解出輸出功率序列的高頻分量和低頻分量,並通過重構得到天氣相關特徵值。從高頻分量可以明顯反映天氣狀況,在晴朗條件下,高頻部分非常平穩,而在天氣雲量較大時,高頻部分變化較大。
再次,構造晴空指數。晴空指數指入射到水平面的實際輻射與晴空條件下的理論輻射之比,表達式為,
其中,Gt為入射到水平面的實際輻射度,入射到水平面的實際輻射。
步驟4,計算輸入變量的影響因子
以步驟2中經過預處理的數據和步驟3中引入的新變量作為輸入變量,首先,採用Gamma Test對輸入變量的噪聲方差進行估計,方法如下:
計算輸入空間中點xi與其第k個最鄰近點間距離的平均值為,
其中,k的範圍是1≤k≤kmax,xN[i,k]表示與xi最鄰近的向量,i的範圍是1≤i≤M。
計算對應輸出數據之間的平均距離為,
其中,yN[i,k]是xi的第k個最鄰近點對應的輸出。
構造線性方程為,
γM(k)=Γ+AδM(k)
其中Γ代表輸入變量的噪聲方差。
其次,構造適應度函數。採用如下適應度函數:
其中,gΓ和gA是懲罰項,分別是Γ和A的函數,wΓ和wA是指定值,xi'為輸入向量。
再次,採用NSGA-II多目標遺傳算法對輸入變量的影響因子進行計算。
計算發現,影響因子為1的變量有:直射輻射度、水平總輻射度、時角、功率小波分析數據、傾斜面總輻射度、風速、輸出功率、晴空指數,影響因子為0的變量有:組件溫度、環境溫度、環境溼度、大氣壓、空氣可見度、風向、天氣類型。
步驟5,構造降維後的輸入特徵向量
根據步驟4中輸入變量的影響因子確定降維後的輸入變量,構造輸入特徵向量。
步驟6,建立光伏出力預測模型
根據步驟5構造的輸入特徵向量作為樣本序列,採用SVM支持向量機模型對樣本進行訓練,得到光伏出力預測模型。其預測的基本過程如下:
首先,根據模型假設選定因變量和果變量,其次,對數據進行預處理,第三,交叉驗證選擇回歸的最佳參數,第四,利用最佳參數訓練SVM,第五,進行擬合預測,得到預測指標。
對預測結果進行誤差分析,發現:該方法實現在天氣異變度較低時相對均方根誤差分別為9.7%,9.1%,7.8%;異變度較高時分別為13.54%,13.36%,13.87%的預測精度。
最後,還需要注意的是,以上列舉的僅是本發明的一個具體實施例。顯然,本發明不限於以上實施例,還可以有許多變形。本領域的普通技術人員能從本發明公開的內容直接導出或聯想到的所有變形,均應認為是本發明的保護範圍。
