基於雜波空時等效的三維異構陣空時重構方法與流程
2023-04-29 06:44:36 3
本發明屬於雷達技術領域,尤其涉及一種基於雜波空時等效的三維異構陣空時重構方法,用於機載共形陣雷達信號處理。
背景技術:
現代戰爭對機載雷達的隱身能力、機動能力和目標探測能力都提出了越來越高的要求,而機載雷達採用的天線,或外露於機體,或裝於流線形的整流罩內,從機頭到機尾分布著多達幾十種類型各異的天線,這不僅大大影響了飛機的氣動性能和隱身性能,而且也限制了很多電子設備的性能。因此,研究能夠與飛行載體表面相吻合的天線系統-三維異構陣,成為近年來日益重視的新領域。機載三維陣雷達,由於其便於集成,能減小載機負荷和雷達散射截面積等獨特優勢,成為相控陣雷達的重要發展方向。
早在20世紀60年代,國外就已經開始了對三維異構陣的研究,包括美國、以色列、日本和歐洲。例如,美國空軍提出的宇航飛行器「智能蒙皮計劃」(penval),其本質就是將多副天線與飛行器載體有效共形的研究計劃。我國在20世紀90年代也開始進行了研究。目前,三維異構陣已受到各國軍方的高度關注,並且已有世界頂級戰機、預警機採用了三維異構陣以支持其先進的機載雷達和卓越的氣動-隱身外形。
但是,不同於平面相控陣,三維異構陣接收的雜波特性將變得十分複雜,這種複雜性主要體現在陣元通道間的互耦特性更加複雜、陣元通道間的極化特性更加複雜、陣元/子陣相位中心非線性排列、雜波存在極化去相關問題等,這種雜波特性的複雜性也給雜波抑制帶來很大的問題,包括陣列流型更加複雜,目標和雜波的導向矢量計算困難,導向矢量間的相關性更難計算,幹擾子空間和目標導向矢量的關係難以確定,雜波秩顯著增加等。在雜波抑制性能方面,由於機載雷達的平臺運動,在不同的方向,雜波往往都呈現出一定的非平穩性,在近距離探測時這種非平穩性尤其嚴重,這導致了三維異構陣在形成接收方向圖時的旁瓣性能不穩定,使得傳統的空時自適應處理算法在三維異構陣雷達的雜波抑制中性能嚴重下降。
技術實現要素:
針對上述現有技術的缺點,本發明的目的在於提供一種基於雜波空時等效的三維異構陣空時重構方法,能夠解決三維異構陣雷達在形成接收方向圖時的旁瓣性能不穩定導致的雜波抑制性能下降的問題。
為達到上述目的,本發明採用如下技術方案予以實現。
一種基於雜波空時等效的三維異構陣空時重構方法,所述方法包括如下步驟:
步驟1,設定雷達的三維異構陣為圓臺陣,所述圓臺陣共包含m層陣元,將每層陣元作為圓臺陣的一個子陣,則所述圓臺陣包含m個子陣;獲取所述圓臺陣接收到的雜波回波數據,所述圓臺陣接收到的雜波回波數據包含l個距離單元的回波數據矢量;
令l=1;l表示第l個距離單元,l=1,2,...,l;
步驟2,獲取第l個距離單元的回波數據矢量,將所述第l個距離單元的回波數據矢量重新排列為回波數據矩陣,得到第l個距離單元的回波數據矩陣,所述第l個距離單元的回波數據矩陣為k行m列的矩陣,其中,所述第l個距離單元的回波數據矩陣的第m列表示第m個子陣接收到的回波數據,所述第l個距離單元的回波數據矩陣的第k行表示第k個脈衝時刻接收到的回波數據,m=1,...,m,k=1,...,k;m為圓臺陣包含的子陣數據,k為雷達在一個相干處理間隔內發射的脈衝個數,且k遠大於m;
步驟3,對所述第l個距離單元的回波數據矩陣中的第m個子陣接收到的回波數據分別做m-m個元素的循環向上移動,且m分別取1,2,...,m;得到第l個距離單元的重排後的回波數據矩陣;
步驟4,刪除所述第l個距離單元的重排後的回波數據矩陣中相位不一致的後m-1行,得到第l個距離單元的空時重構回波數據,所述第l個距離單元的空時重構回波數據為k-m+1行m列;
步驟5,令l的值加1,並依次重複執行步驟2至步驟4,分別得到l個距離單元中每個距離單元的空時重構回波數據。
本發明技術方案的特點和進一步的改進為:
(1)在步驟5之後,所述方法還包括:
步驟6,對所述第l個距離單元的空時重構回波數據中的第k′個都卜勒通道數據作離散傅立葉變換,得到第l個距離單元的空時重構回波數據中第k′個都卜勒通道離散傅立葉變換後的數據,其中,k′依次取1,2,...,k-m+1,從而得到第l個距離單元的空時重構回波數據中k-m+1個都卜勒通道離散傅立葉變換後的數據;
步驟7,令l分別取1,2,...,l,從而得到l個距離單元中每個距離單元的空時重構回波數據中k-m+1個都卜勒通道離散傅立葉變換後的數據;
步驟8,對l個距離單元的空時重構回波數據中第k′個都卜勒通道離散傅立葉變換後的數據進行空域濾波,令k′依次取1,2,...,k-m+1,得到l個距離單元的空時重構回波數據的濾波結果,並將所述l個距離單元的空時重構回波數據的濾波結果作為雜波抑制結果。
(2)步驟2中,
獲取第l個距離單元的回波數據矢量xl為:xl=[x11,x12,...,x1m;x21,x22,...,x2m;...,xkm,...;xk1,xk2,...,xkm]t;
其中,[·]t表示轉置操作,xkm為第k個脈衝時刻第m個子陣的回波數據,且
其中,i=1,...,i表示回波數據中的第i個雜波塊,i為第l個距離單元內的雜波塊數目,ai表示第i個雜波塊的幅度,fsi表示第i個雜波塊的歸一化空間頻率,fdi表示第i個雜波塊的歸一化都卜勒頻率;
且第i個雜波塊的歸一化空間頻率第i個雜波塊的歸一化都卜勒頻率其中,d為子陣間距,φa為天線錐角,λ為雷達工作波長,v為平臺速度,t為脈衝重複間隔;
令第i個雜波塊的歸一化空間頻率與第i個雜波塊的歸一化都卜勒頻率相等,則平臺速度v、脈衝重複間隔t以及子陣間距d存在如下關係d=2vt。
(3)步驟2中,
將所述第l個距離單元的回波數據矢量xl重新排列為回波數據矩陣,得到第l個距離單元的回波數據矩陣xl,具體為:
其中,xl∈ck×m,ck×m表示k行m列的複數矩陣,且xl的行表示時域回波數據,xl的列表示空域回波數據;
令第i個雜波塊的歸一化空間頻率與第i個雜波塊的歸一化都卜勒頻率相等時,第l個距離單元的回波數據矩陣xl為:
(4)步驟3中,對所述第l個距離單元的回波數據矩陣中的第m個子陣接收到的回波數據分別做m-m個元素的循環向上移動,具體為:
對第l個距離單元的回波數據矩陣xl的第m列的回波數據元素做m-m個元素的循環向上移動,從而得到第l個距離單元的重排後的回波數據矩陣
其中,ck×m表示k行m列的複數矩陣。
(5)步驟4中,刪除所述第l個距離單元的重排後的回波數據矩陣中相位不一致的後m-1行,得到第l個距離單元的空時重構回波數據為:
其中,表示行m列的複數矩陣,且
(6)步驟6具體為:
(6a)構造與所述第l個距離單元的空時重構回波數據相對應的變換矩陣f:
其中,表示行列的複數矩陣;
(6b)所述變換矩陣f的第k′列fk′:k′表示第k′個都卜勒通道;
(6c)對所述第l個距離單元的空時重構回波數據中的第k′個都卜勒通道數據作離散傅立葉變換,得到第l個距離單元的空時重構回波數據中第k′個都卜勒通道數據
其中,c1×m表示1行m列的複數矩陣;
(6d)令k′依次取1,2,...,k-m+1,重複執行子步驟(6b)和(6c),從而得到第l個距離單元的空時重構回波數據中k-m+1個都卜勒通道數據。
(7)步驟8具體為:
(8a)獲取l個距離單元的空時重構回波數據中第k′個都卜勒通道數據yk′:其中,yk′∈cm×l,cm×l表示m行l列的複數矩陣,表示第l個距離單元的空時重構回波數據中第k′個都卜勒通道數據,(·)t表示轉置操作;
(8b)採用如下約束表達式,求解最優濾波權向量w:
其中,e{·}表示求期望運算,為第k′個都卜勒通道的回波協方差矩陣,s為空時導向矢量;
求解上述約束表達式,得到最優濾波權向量w=λr-1s,其中,λ=1/(shr-1s);(·)h表示共軛轉置操作,(·)-1表示求逆操作,||·||2表示求模值平方操作;
(8c)根據所述最優濾波權向量w對l個距離單元的空時重構回波數據中第k′個都卜勒通道數據yk′進行空域濾波,得到第k′個都卜勒通道的濾波輸出yk′=whyk′;
(8d)令k′依次取1,2,...,k-m+1,重複執行子步驟(8a)至(8c),得到l個距離單元的空時重構回波數據的濾波結果。
本發明與現有技術相比具有以下優點:
(1)三維異構陣是三維天線結構,由於其在方位向和俯仰向的非線性結構、通道幅相誤差等原因,形成接收方向圖時旁瓣水平抬升,經脈衝-都卜勒濾波後造成相應的旁瓣雜波剩餘功率增加,對雜波抑制性能也是不利的。本發明採用基於雜波空時等效的三維異構陣空時重構方法,可以將三維陣列等效為平面陣列,改善雜波的抑制性能;(2)機載雷達存在平臺運動,這將導致三維陣的某一空間位置不能接收所有的脈衝回波,引起雜波的都卜勒頻譜展寬。本發明將原始回波數據進行空時重構處理,當載機速度與脈衝重複間隔滿足dpca條件時,可以達到所有陣元在同一時刻的相位一致,使得雜波相消結果更穩定、更徹底,從而提高了雜波區的抑制性能;(3)本發明並未局限於理想條件,在平臺速度不穩定即不滿足dpca條件的情況下,其改善性能仍然優於傳統濾波方法,大大擴展了本發明的應用場合。本發明的基於雜波空時等效的三維異構陣空時重構方法不僅可以應用於雜波抑制處理,也可以應用於目標檢測領域。
附圖說明
為了更清楚地說明本發明實施例或現有技術中的技術方案,下面將對實施例或現有技術描述中所需要使用的附圖作簡單地介紹,顯而易見地,下面描述中的附圖僅僅是本發明的一些實施例,對於本領域普通技術人員來講,在不付出創造性勞動的前提下,還可以根據這些附圖獲得其他的附圖。
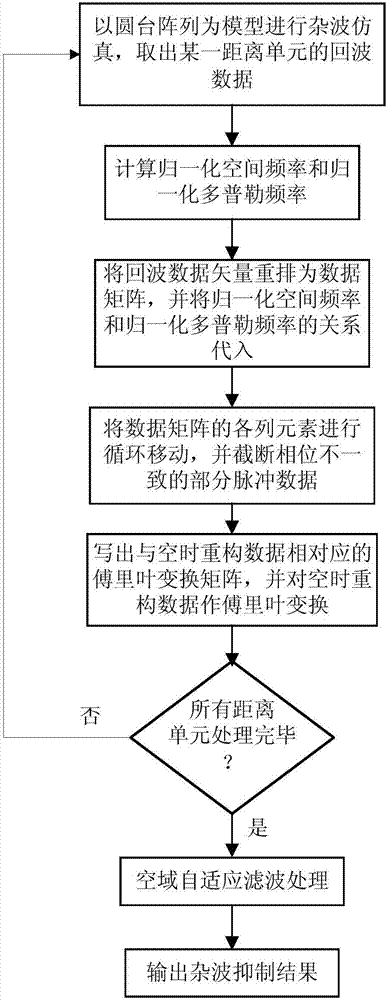
圖1為本發明實施例提供的基於雜波空時等效的三維異構陣空時重構方法的流程示意圖;
圖2為本發明實施例提供的圓臺陣的數據空時重構示意圖;
圖3為本發明實施例提供的對原始回波數據與本發明空時重構數據作stap雜波抑制後的平均雜波剩餘功率對比曲線示意圖;
圖4為本發明實施例提供的對原始回波數據與本發明空時重構數據作stap雜波抑制後的改善因子對比曲線示意圖;
圖5為本發明實施例提供的主雜波區附近的某都卜勒通道,對原始回波數據與本發明空時重構數據作stap雜波抑制後的改善因子隨dpca比例變化曲線示意圖。
具體實施方式
下面將結合本發明實施例中的附圖,對本發明實施例中的技術方案進行清楚、完整地描述,顯然,所描述的實施例僅僅是本發明一部分實施例,而不是全部的實施例。基於本發明中的實施例,本領域普通技術人員在沒有做出創造性勞動前提下所獲得的所有其他實施例,都屬於本發明保護的範圍。
本發明實施例提供一種基於雜波空時等效的三維異構陣空時重構方法,如圖1所示,所述方法包括如下步驟:
步驟1,設定雷達的三維異構陣為圓臺陣,所述圓臺陣共包含m層陣元,將每層陣元作為圓臺陣的一個子陣,則所述圓臺陣包含m個子陣;獲取所述圓臺陣接收到的雜波回波數據,所述圓臺陣接收到的雜波回波數據包含l個距離單元的回波數據矢量。
令l=1;l表示第l個距離單元,l=1,2,...,l。
假設三維異構陣列模型為圓臺陣,該圓臺共包含m層陣元,每層陣元數量不等,將每一層陣元劃分為一個子陣,則可劃分為m個子陣,圓臺的所有陣元數目為n。子陣間距為d,雷達工作波長為λ,且滿足d=λ/2。平臺速度向量為v,其方向為x軸正向,天線軸向與向量v的夾角為0。。雷達在一個相干處理間隔內的發射脈衝數目為k。
步驟2,獲取第l個距離單元的回波數據矢量,將所述第l個距離單元的回波數據矢量重新排列為回波數據矩陣,得到第l個距離單元的回波數據矩陣,所述第l個距離單元的回波數據矩陣為k行m列的矩陣,其中,所述第l個距離單元的回波數據矩陣的第m列表示第m個子陣接收到的回波數據,所述第l個距離單元的回波數據矩陣的第k行表示第k個脈衝時刻接收到的回波數據,m=1,...,m,k=1,...,k;m為圓臺陣包含的子陣數據,k為雷達在一個相干處理間隔內發射的脈衝個數,且k遠大於m。
步驟2中,由於這裡僅考慮子陣間的相位關係,所以將每一層的各個陣元之間接收信號的相位時延忽略不計。
獲取第l個距離單元的回波數據矢量xl為:xl=[x11,x12,...,x1m;x21,x22,...,x2m;...,xkm,...;xk1,xk2,...,xkm]t;
其中,[·]t表示轉置操作,xkm為第k個脈衝時刻第m個子陣的回波數據,且
其中,i=1,...,i表示回波數據中的第i個雜波塊,i為第l個距離單元內的雜波塊數目,ai表示第i個雜波塊的幅度,fsi表示第i個雜波塊的歸一化空間頻率,fdi表示第i個雜波塊的歸一化都卜勒頻率;
且第i個雜波塊的歸一化空間頻率第i個雜波塊的歸一化都卜勒頻率其中,d為子陣間距,φa為天線錐角,λ為雷達工作波長,v為平臺速度,t為脈衝重複間隔;
根據上述公式,可得到歸一化空間頻率和歸一化都卜勒頻率之間存在如下關係:
fdi=βfsi
其中β稱為歸一化坐標的雜波脊斜率,由於天線軸向與速度夾角為零,
則當平臺速度v、脈衝重複間隔t與子陣間距d之間滿足dpca(displacedphasecenterantenna,偏置相位中心天線)條件時,即d=2vt,那麼在一個脈衝重複間隔內,圓臺陣的移動距離為一個子陣間距,此時β=1,那麼得到歸一化空間頻率與歸一化都卜勒頻率的關係為:
fsi=fdi
以下推導均以此條件為前提。
令第i個雜波塊的歸一化空間頻率與第i個雜波塊的歸一化都卜勒頻率相等,則平臺速度v、脈衝重複間隔t以及子陣間距d存在如下關係d=2vt。
進一步的,以時域為行,空域為列,將所述第l個距離單元的回波數據矢量xl重新排列為回波數據矩陣,得到第l個距離單元的回波數據矩陣xl,具體為:
其中,xl∈ck×m,ck×m表示k行m列的複數矩陣,且xl的行表示時域回波數據,xl的列表示空域回波數據;
令第i個雜波塊的歸一化空間頻率與第i個雜波塊的歸一化都卜勒頻率相等時,第l個距離單元的回波數據矩陣xl為:
步驟3,對所述第l個距離單元的回波數據矩陣中的第m個子陣接收到的回波數據分別做m-m個元素的循環向上移動,且m分別取1,2,...,m;得到第l個距離單元的重排後的回波數據矩陣。
步驟3中,對所述第l個距離單元的回波數據矩陣中的第m個子陣接收到的回波數據分別做m-m個元素的循環向上移動,具體為:
對第l個距離單元的回波數據矩陣xl的第m列的回波數據元素做m-m個元素的循環向上移動,從而得到第l個距離單元的重排後的回波數據矩陣
其中,ck×m表示k行m列的複數矩陣。
示例性的,如圖2所示,三維圓臺陣的外形類似於圓錐形狀,圓臺軸向為x軸正向,與載機速度方向一致。為方便理解,僅畫了示意圖,該圖中的圓臺陣共兩層圓環陣,即兩個子陣,沿x軸正向的第1個子陣包含2個陣元,第2個子陣包含1個陣元。圖中畫了3個脈衝重複間隔的時間內圓臺陣的運動情況。觀察該圖可發現,當平臺速度滿足dpca條件時,在接收脈衝信號的一個脈衝重複間隔內,圓臺陣層級的子陣剛好移動一個子陣間距,例如在圖2中,圓臺陣的第2個子陣剛好與下一個脈衝重複間隔的第1個子陣處於相同的空間位置。
接下來,通過對數據的循環移動和截斷處理,使得處在同一個空間位置的各脈衝數據作為同一個時域通道的數據,從而達到同一空間位置的相位一致。具體化為,將數據矩陣xl中的第m個子陣的空域通道數據作m-m個元素的向上循環移動,對於矩陣表達式來說,就是把矩陣的第m列中的各元素作m-m個元素的向上循環移動,其中m=1,...,m,則數據矩陣的表達式變為:
從上式的矩陣表達式中可以看出,矩陣的第1行至第k-m+1行中各個空域通道數據完成了相位對齊操作。
步驟4,刪除所述第l個距離單元的重排後的回波數據矩陣中相位不一致的後m-1行,得到第l個距離單元的空時重構回波數據,所述第l個距離單元的空時重構回波數據為k-m+1行m列。
為實現相位一致,需要保留各個陣元之間相位對齊的部分數據,並對相位不一致的部分脈衝數據進行截斷操作,即保留矩陣中的前k-m+1行,最終得到空時重構數據。
步驟4中,刪除所述第l個距離單元的重排後的回波數據矩陣中相位不一致的後m-1行,得到第l個距離單元的空時重構回波數據為:
其中,表示行m列的複數矩陣,且
這樣,所有空間位置接收的雜波數據達到相位一致,完成了數據的空時重構處理。
步驟5,令l的值加1,並依次重複執行步驟2至步驟4,分別得到l個距離單元中每個距離單元的空時重構回波數據。
步驟6,對所述第l個距離單元的空時重構回波數據中的第k′個都卜勒通道數據作離散傅立葉變換,得到第l個距離單元的空時重構回波數據中第k′個都卜勒通道離散傅立葉變換後的數據,其中,k′依次取1,2,...,k-m+1,從而得到第l個距離單元的空時重構回波數據中k-m+1個都卜勒通道離散傅立葉變換後的數據。
採用fa(factoredapproach,因子化)方法,首先對空時重構數據作傅立葉變換,使得數據從時域轉換到都卜勒域,然後再對某一都卜勒通道的空域數據作自適應濾波處理。
步驟6具體為:
(6a)構造與所述第l個距離單元的空時重構回波數據相對應的變換矩陣f:
其中,表示行列的複數矩陣;
(6b)所述變換矩陣f的第k′列fk′:k′表示第k′個都卜勒通道;
(6c)對所述第l個距離單元的空時重構回波數據中的第k′個都卜勒通道數據作離散傅立葉變換,得到第l個距離單元的空時重構回波數據中第k′個都卜勒通道離散傅立葉變換後的數據
其中,c1×m表示1行m列的複數矩陣;
(6d)令k′依次取1,2,...,k-m+1,重複執行子步驟(6b)和(6c),從而得到第l個距離單元的空時重構回波數據中k-m+1個都卜勒通道離散傅立葉變換後的數據。
步驟7,令l分別取1,2,...,l,從而得到l個距離單元中每個距離單元的空時重構回波數據中k-m+1個都卜勒通道數據。
步驟8,對l個距離單元的空時重構回波數據中第k′個都卜勒通道離散傅立葉變換後的數據進行空域濾波,令k′依次取1,2,...,k-m+1,得到l個距離單元的空時重構回波數據的濾波結果,並將所述l個距離單元的空時重構回波數據的濾波結果作為雜波抑制結果。
步驟8具體為:
(8a)獲取l個距離單元的空時重構回波數據中第k′個都卜勒通道離散傅立葉變換後的數據yk′:其中,yk′∈cm×l,cm×l表示m行l列的複數矩陣,表示第l個距離單元的空時重構回波數據中第k′個都卜勒通道離散傅立葉變換後的數據,(·)t表示轉置操作;
(8b)採用如下約束表達式,求解最優濾波權向量w:
其中,e{·}表示求期望運算,為第k′個都卜勒通道離散傅立葉變換後的的回波協方差矩陣,s為空時導向矢量;w=[w1,w2,...,wm]t,且w∈cm×1。
求解上述約束表達式,得到最優濾波權向量w=λr-1s,其中,λ=1/(shr-1s);(·)h表示共軛轉置操作,(·)-1表示求逆操作,||·||2表示求模值平方操作;
(8c)根據所述最優濾波權向量w對l個距離單元的空時重構回波數據中第k′個都卜勒通道離散傅立葉變換後的數據yk′進行空域濾波,得到第k′個都卜勒通道的濾波輸出yk′=whyk′;
(8d)令k′依次取1,2,...,k-m+1,重複執行子步驟(7a)至(7c),得到l個距離單元的空時重構回波數據的濾波結果。
觀察步驟(6c),對空時重構數據作傅立葉變換後,將這樣的數據作雜波相消的抑制結果更穩定、更徹底。這是因為用於估計雜波協方差矩陣的距離樣本雖為獨立同分布樣本,但是針對每個距離單元的數據幅度只是統計意義上的平均水平,不同的距離單元,數據幅度依然存在差距而非完全相等;且不同距離單元、不同雜波塊的空間頻率也不同。
那麼,對原始回波數據進行fa方法處理後的空域自適應濾波處理過程,具體化為,對1號空域通道數據濾波,是利用2號空域通道數據作加權處理並與其進行雜波相消,對每個雜波塊來說,相同的權矢量無法保證完全對消,即:xk′l(1)-whxk′l(2)≠0;
而將回波數據進行重排、截斷處理後,兩空域通道數據的幅度、相位一致,總能找到適當的權矢量,將雜波相消的更為徹底,即:
因此,基於雜波空時等效的空時重構方法能夠很好的對消旁瓣雜波,同時在主雜波區較傳統濾波處理也有較好的抑制性能。
對於空間的所有陣元來說,雜波的時間採樣均為同步採樣,空間採樣僅與空間位置或角度有關,與採樣時間無關,類似於時間採樣僅與採樣時間有關,與空間位置無關,即為所謂的雜波空時等效特性。基於這一特性,當沒有平臺運動且忽略各種誤差的情況下,同一空間採樣位置能夠接收到所有脈衝信號,且所有陣元在同一時刻的相位一致。而機載雷達存在平臺運動,導致三維陣的某一空間位置不能接收所有的脈衝回波,引起雜波的都卜勒頻譜展寬,那麼當載機速度與脈衝重複頻率滿足dpca條件時,可以利用脈衝之間的轉換來補償平臺運動,將空時數據重排,以達到所有陣元在同一時刻的相位一致,並將相位不一致的部分截斷使得體陣列轉換為面陣列,實現數據的空時重構,提高雜波的抑制性能。
下面結合仿真實驗對本發明的效果做進一步說明。
1)仿真參數
本發明是一種基於雜波空時等效的三維異構陣空時重構方法,可用於三維異構陣列的雜波抑制和目標檢測。
本發明採用的三維異構陣列模型為圓臺形狀。圓臺陣列共包含6圈陣元,每一圈陣元數量不等,將圓臺陣的6圈陣元劃分為6個子陣,子陣間距為半波長,初始載機速度滿足dpca條件。那麼,將以圓臺陣列為天線模型的雜波仿真數據進行空時重構後,對於陣列來說,是將圓臺形狀轉換為同心圓環形狀。這樣便完成了對圓臺陣的空時數據重構處理。詳細的系統參數參照下表。
2)仿真數據處理結果及分析
為了說明本發明性能的優越性,給出了原始數據作空時自適應處理(spacetimeadaptiveprocessing,stap)雜波抑制以及本發明對空時重構數據作stap雜波抑制的處理結果對比圖。
此處採用的傳統stap方法為efa方法,相比於fa方法,它在時域使用了相鄰的三個都卜勒通道進行空時聯合處理,由於增加了時域自由度,有助於改善雜波抑制性能,也能更好地體現本發明所提方法的優勢。
參照圖3,為某遠程距離門內對原始回波數據與本發明空時重構數據作stap雜波抑制後的平均雜波剩餘功率對比曲線。圖中的縱坐標表示功率的大小,單位為分貝(db),橫坐標為都卜勒通道,共64個。圖例中的原始數據即為運用stap中的efa方法對原始回波數據作雜波抑制處理,在圖中用虛線表示;圖例中的空時重構表示本發明中的基於雜波空時等效的三維異構陣空時重構方法,它運用stap中的efa方法對空時重構之後的數據進行雜波抑制處理,在圖中用實線表示。從圖3可以看出,採用本發明中的空時重構方法經過stap處理後,平均雜波剩餘功率更低,取得了優於傳統stap方法的雜波抑制效果。
參照圖4,為對原始回波數據與本發明空時重構數據作stap雜波抑制後的改善因子對比曲線。圖中的縱坐標表示改善因子的大小,單位為分貝(db),橫坐標為都卜勒通道,共64個。圖例中的原始數據即為運用stap中的efa方法對原始回波數據作雜波抑制處理後的改善因子,在圖中用虛線表示;圖例中的空時重構表示本發明中的基於雜波空時等效的三維異構陣空時重構方法,它運用stap中的efa方法對空時重構之後的數據進行雜波抑制處理後的改善因子,在圖中用實線表示。由wardj在其文獻中指出,為使因估計不準確而帶來的性能損失在3db以內,要求樣本數目至少為協方差矩陣階數(或自由度)的兩倍,本發明所用的獨立同分布樣本數目滿足樣本條件。從圖4可以看出,採用本發明中的空時重構方法經過stap處理後,相較於傳統濾波方法改善了3.1db。
觀察圖3和圖4可以看出,當平臺速度滿足dpca條件時,將原始數據進行空時重構處理有很好的雜波對消效果,較傳統濾波處理改善了雜波旁瓣水平,在主雜波區也有較好的抑制性能。
參照圖5,為主雜波區附近的第30號都卜勒通道,對原始回波數據與本發明空時重構數據作stap雜波抑制後的改善因子隨dpca比例變化曲線。圖中的縱坐標表示本發明空時重構數據與原始回波數據分別作stap雜波抑制後的改善因子差值,單位為分貝(db),橫坐標為dpca比例,即實際速度與理想速度之比,比例範圍是0.4-1.4。從圖5可以看出,在所有比例範圍內,兩者差值均大於0,這表明即使平臺速度偏離了理想的dpca條件,本發明所用方法相比於傳統濾波方法仍然有更優的雜波抑制效果。
綜上,本發明提出的一種基於雜波空時等效的三維異構陣空時重構方法,主要解決三維異構陣列的體陣列結構帶來的接收方向圖時的旁瓣性能不穩定導致的雜波抑制性能下降的問題。本發明利用雜波的空時等效特性,當載機速度與脈衝重複頻率滿足dpca條件時,對空時數據進行重排、截斷處理,以滿足所有空間位置的相位一致性,達到更好的雜波對消效果。當載機速度不穩定時,本發明方法的雜波抑制性能仍然優於傳統濾波方法。因此更提升了本發明方法的應用價值。
本領域普通技術人員可以理解:實現上述方法實施例的全部或部分步驟可以通過程序指令相關的硬體來完成,前述的程序可以存儲於計算機可讀取存儲介質中,該程序在執行時,執行包括上述方法實施例的步驟;而前述的存儲介質包括:rom、ram、磁碟或者光碟等各種可以存儲程序代碼的介質。
以上所述,僅為本發明的具體實施方式,但本發明的保護範圍並不局限於此,任何熟悉本技術領域的技術人員在本發明揭露的技術範圍內,可輕易想到變化或替換,都應涵蓋在本發明的保護範圍之內。因此,本發明的保護範圍應以所述權利要求的保護範圍為準。
