一種心電動力學數據量化分析方法與流程
2023-05-16 08:59:02 1
本發明涉及心電檢測技術領域,尤其涉及一種心電動力學數據量化分析方法。
背景技術:
長期以來,心血管疾病已被公認為是危害人類生命健康最嚴重的疾病之一,其中,由於心肌缺血導致的心肌梗塞的發病率和死亡率更是高居各類疾病之首。由於部分心肌缺血的患者在發病早期並沒有明顯的臨床症狀或者病症比較輕微,因此使得病情十分容易被忽視。
現有技術中,對於心肌缺血,在理論上有一定的檢測手段,即採用體表心電圖(electrocardiogram,ecg)在臨床上對心臟特徵進行持續地觀察和診斷。但是現有技術中對於心電圖中的心電數據通常只做較為粗糙的圖像化檢測,並沒有定量描述和檢測的手段,因此使得心電檢測結果的準確性不高,進而難以把握心電數據中的細微變化,從而有可能在檢測過程中遺漏患者的一些心臟異常情況例如心肌缺血病症等。醫生在觀察心電圖等心電數據的過程中,通常也只能做主觀的定性判斷,從而在一定程度上影響了最終結果的準確性。
技術實現要素:
根據現有技術中存在的上述問題,現提供一種心電動力學數據量化分析方法的技術方案,旨在對心電動力學數據進行定量描述,提供了有效的量化指標,為醫生採用心電向量圖進行病情診斷提供了便利。
上述技術方案具體包括:
一種心電動力學數據量化分析方法,其特徵在於,包括:
步驟s1,採集得到心電數據;
步驟s2,根據採集到的所述心電數據獲取對應的心電動力學數據;
步驟s3,提取所述心電動力學數據的空間離散量化特徵,以及提取所述心電動力學數據的時間離散量化特徵;
步驟s4,根據所述空間離散量化特徵和所述時間離散量化特徵形成所述心電動力學數據的量化信息,並根據所述量化信息對所述心電向量圖進行量化分析。
優選的,該心電動力學數據量化分析方法,其特徵在於,所述步驟s2中,獲取所述心電動力學數據的步驟具體包括:
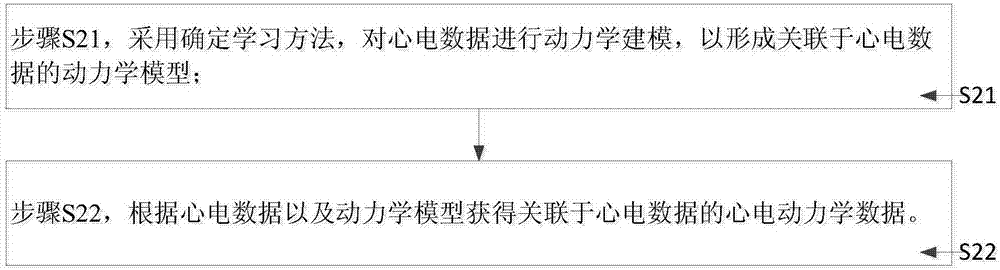
步驟s21,採用確定學習方法,對所述心電數據進行動力學建模,以形成關聯於所述心電數據的動力學模型;
步驟s22,根據所述心電數據以及所述動力學模型獲得關聯於所述心電數據的所述心電動力學數據。
優選的,該心電動力學數據量化分析方法,其特徵在於,所述心電動力學數據中包括以三維空間形式排布的多個數據點;
則所述步驟s3中,獲取所述心電動力學數據的所述空間離散量化特徵的步驟具體包括:
步驟s31a,將所述心電動力學數據按照時間順序處理得到各個所述數據點的指數變化率;
步驟s32a,將所有所述數據點的所述指數變化率整合成所述空間離散量化特徵。
優選的,該心電動力學數據量化分析方法,其特徵在於,所述步驟s31a具體包括:
步驟s311a,處理得到所述心電動力學數據中所述數據點的初始距離集合;
步驟s312a,處理得到所述數據點的對應的結束距離集合;
步驟s313a,根據所述初始距離集合以及所述結束距離集合分別處理得到每個所述數據點的所述指數變化率。
優選的,該心電動力學數據量化分析方法,其特徵在於,所述步驟s311a中,依照下述公式處理得到所述初始距離集合:
其中,
i=1,2,…,ik;
xk用於表示當前第k個所述數據點;
為xk的一臨近點集,用於表示與xk在空間距離上最近的a1個點的點集;
ik用於表示第k步所述臨近點集的元素總數,並且ik≤a1;
為所述初始距離集合,用於表示與xk之間的距離集合。
優選的,該心電動力學數據量化分析方法,其特徵在於,所述步驟s312a中,依照下述公式處理得到所述結束距離集合:
其中,
i=1,2,…,ik,δ∈n;
xk用於表示當前第k個所述數據點;
xk+δ用於表示將xk的時間往前增加δ步得到的所述數據點;
為xk的一臨近點集,用於表示與xk在空間距離上最近的a1個點的點集;
用於表示將的時間往前增加δ步得到的點集;
ik用於表示第k步所述臨近點集的元素總數,並且ik≤a1;
為所述結束距離集合,用於表示與xk分別往前增加δ步後的距離集合。
優選的,該心電動力學數據量化分析方法,其特徵在於,所述步驟s313a中,將所述初始距離集合和所述結束距離集合中的每一對應項進行對數計算,以得到每個所述數據點的所述指數變化率。
優選的,該心電動力學數據量化分析方法,其特徵在於,所述步驟s32a中,採用非負平均的方法將所有所述數據點的所述指數變化率整合成所述空間離散量化特徵。
優選的,該心電動力學數據量化分析方法,其特徵在於,所述心電動力學數據為多維度數據;
則所述步驟s3中,獲取所述心電動力學數據的所述時間離散量化特徵的步驟具體包括:
步驟s31b,分別將每一維度的所述心電動力學數據轉換為對應的頻域數據;
步驟s32b,採用一預設的特徵函數組分別與每一維度的所述頻域數據進行擬合,以得到每一維度的時間離散度特徵分量;
步驟s33b,綜合所有維度的所述時間離散度特徵分量形成所述心電動力學數據的所述時間離散量化特徵。
優選的,該心電動力學數據量化分析方法,其特徵在於,所述步驟s31b中,採用快速傅立葉變化方法分別將每一維度的所述心電動力學數據轉換為對應的頻域數據。
優選的,該心電動力學數據量化分析方法,其特徵在於,所述步驟s33b中,採用幾何平均的方法綜合所有維度的所述時間離散度特徵分量形成所述心電動力學數據的所述時間離散量化特徵。
優選的,該心電動力學數據量化分析方法,其特徵在於,所述步驟s4中,
於一xoy坐標平面中,採用所述時間離散量化特徵和所述空間離散量化特徵中的一個作為對應的所述心電動力學數據的x軸坐標,以及採用所述時間離散量化特徵和所述空間離散量化特徵中的另一個作為對應的所述心電動力學數據的y軸坐標,以形成所述心電動力學數據的坐標信息;
將所述坐標信息作為所述心電動力學數據的所述量化信息。
優選的,該心電動力學數據量化分析方法,其特徵在於,預先將所述xoy坐標平面劃分為第一區域、第二區域以及第三區域;
當所述量化信息表示所述心電動力學數據落入所述第一區域中時,表示對應的所述心電向量圖表示的心臟體徵正常;
當所述量化信息表示所述心電動力學數據落入所述第二區域中時,表示對應的所述心電向量圖表示的心臟體徵異常;
當所述量化信息表示所述心電動力學數據落入所述第三區域中時,表示對應的所述心電向量圖表示的心臟體徵疑似異常。
上述技術方案的有益效果是:提供一種心電動力學數據量化分析方法,能夠對心電數據進行定量描述,提供有效的量化指標,為醫生採用心電向量圖進行病情診斷提供了便利。
附圖說明
圖1是本發明的較佳的實施例中,一種心電動力學數據量化分析方法的總體流程示意圖;
圖2是本發明的較佳的實施例中,獲取心電動力學數據的流程示意圖;
圖3-4是本發明的較佳的實施例中,獲取心電動力學數據中的空間離散量化特徵的流程示意圖;
圖5是本發明的較佳的實施例中,獲取心電動力學數據中的時間離散量化特徵的流程示意圖;
圖6是本發明的一個具體的實施例中,心肌梗塞數據的心電動力學數據示意圖;
圖7是本發明的一個具體的實施例中,對心肌梗塞的心電動力學數據進行分析的示意圖。
具體實施方式
下面將結合本發明實施例中的附圖,對本發明實施例中的技術方案進行清楚、完整地描述,顯然,所描述的實施例僅僅是本發明一部分實施例,而不是全部的實施例。基於本發明中的實施例,本領域普通技術人員在沒有作出創造性勞動的前提下所獲得的所有其他實施例,都屬於本發明保護的範圍。
需要說明的是,在不衝突的情況下,本發明中的實施例及實施例中的特徵可以相互組合。
下面結合附圖和具體實施例對本發明作進一步說明,但不作為本發明的限定。
根據現有技術中存在的上述問題,現提供一種心電動力學數據量化分析方法,該方法具體如圖1所示,包括:
步驟s1,採集得到心電數據;
步驟s2,根據採集到的心電數據獲取對應的心電動力學數據;
步驟s3,提取心電動力學數據的空間離散量化特徵,以及提取心電動力學數據的時間離散量化特徵;
步驟s4,根據空間離散量化特徵和時間離散量化特徵形成心電動力學數據的量化信息,並根據量化信息對心電向量圖進行量化分析。
具體地,上述心電數據可以由心電向量圖(vectorcardiogram,vcg)中獲得。所謂心電向量圖,是指主要依據心臟電激動的方向與大小在每一個瞬間是不同的的原理,記錄心臟各瞬間產生的電激動在立體的方向及大小的一種立體圖像。心電向量圖能夠較真實地記錄出心臟動作電流,可用來闡明心電圖產生的原理和解釋心電圖波形,從而提高臨床的診斷效果。心電向量圖和心電圖都是心電活動的反映,僅僅記錄的方法不同。上述步驟s1中,採集得到心電數據的過程為現有技術,在此不再贅述。
本實施例中,隨後根據心電數據進行確定學習動力學建模,從而獲得心電動力學(cdvg)數據。
本實施例中,上述步驟s3中,根據上述心電動力學數據分別提取其中的時間離散量化特徵和空間離散量化特徵,隨後根據時間離散量化特徵和空間離散量化特徵形成上述心電動力學數據的量化信息,該量化信息可用於對心電動力學數據進行定量描述,因此可以根據該量化信息對心電向量圖進行量化分析,以根據分析結果判斷患者是否有異常的心臟體徵。
本發明的較佳的實施例中,上述步驟s2中,獲取心電動力學數據的步驟如圖2所示,具體包括:
步驟s21,採用確定學習方法,對心電數據進行動力學建模,以形成關聯於心電數據的動力學模型;
步驟s22,根據心電數據以及動力學模型獲得關聯於心電數據的心電動力學數據。
具體地,本實施例中,首先對採集得到的心電數據進行確定學習動力學建模,從而獲得對應的心電動力學數據。具體地,把原始的心電數據e(t),e∈r,t=1,2,...,t轉化成心電動力學數據x(t),x∈r3,t=1,2,...,t。
本發明的較佳的實施例中,心電動力學數據中包括以三維空間形式排布的多個數據點;
則上述步驟s3中,獲取心電動力學數據的空間離散量化特徵的步驟具體如圖3所示,包括:
步驟s31a,將心電動力學數據按照時間順序處理得到各個數據點的指數變化率;
步驟s32a,將所有數據點的指數變化率整合成空間離散量化特徵。
具體地,本實施例中,上述心電動力學數據包括以三維空間形式排布的多個數據點,首先對心電動力學數據三維空間數據按照時間順序求得各數據點上的指數變化率,處理該指數變化率的方式(即上述步驟s31a)具體如圖4所示,包括:
步驟s311a,處理得到心電動力學數據中數據點的初始距離集合;
步驟s312a,處理得到數據點的對應的結束距離集合;
步驟s313a,根據初始距離集合以及結束距離集合分別處理得到每個數據點的指數變化率。
具體地,本發明的較佳的實施例中,上述步驟s311a中,依照下述公式處理得到初始距離集合:
其中,
i=1,2,…,ik;
xk用於表示當前第k個數據點;
為xk的一臨近點集,用於表示與xk在空間距離上最近的a1個點的點集;
ik用於表示第k步臨近點集的元素總數,並且ik≤a1;
為初始距離集合,用於表示與xk之間的距離集合。
即上述步驟s311a中,首先標記與心電動力學數據中當前第k個數據點xk空間距離最近的a1個點,並該a1個點的點集計為臨近點集i=1,2,…,ik,其中ik為第k步臨近點集的元素的總數,並且ik≤a1。隨後,將該臨近點集與當前軌跡點(即當前數據點xk)的距離集為初始距離集合,即如上述公式(1)所示。
本發明的較佳的實施例中,上述步驟s312a中,依照下述公式處理得到結束距離集合:
其中,
i=1,2,…,ik,δ∈n;
xk用於表示當前第k個所述數據點;
xk+δ用於表示將xk的時間往前增加δ步得到的所述數據點;
為xk的一臨近點集,用於表示與xk在空間距離上最近的a1個點的點集;
用於表示將的時間往前增加δ步得到的點集;
ik用於表示第k步所述臨近點集的元素總數,並且ik≤a1;
為所述結束距離集合,用於表示與xk分別往前增加δ步後的距離集合。
即上述步驟s312a中,把當前軌跡點xk和臨近點集的時間分別往前增加δ步,從而根據上述公式(2)計算結束距離集合。
本發明的較佳的實施例中,上述步驟s313a中,將初始距離集合和結束距離集合中的每一對應項進行對數計算,以得到每個數據點的指數變化率。上述經過對數運算得到的指數變化率計為i=1,2,…,ik。經過上述過程得到的指數變化率即為指數增長係數集。
本發明的較佳的實施例中,上述步驟s32a中,可以採用非負平均的方法將所有數據點的指數變化率整合成空間離散量化特徵。
具體地,首先,取出當前第k步的非負的指數變化率並記為其中,並且,把j的最大值記為jk。
然後,依照下述公式計算當前的空間離散度係數:
其中,φk用於表示上述空間離散度係數。
最後,進行所有步的平均運算以作為上述空間離散量化特徵。該特徵依照下述公式計算:
本發明的較佳的實施例中,上述心電動力學數據為多維度的數據;
則步驟s3中,獲取心電動力學數據的時間離散量化特徵的步驟具體如圖5所示,包括:
步驟s31b,分別將每一維度的心電動力學數據轉換為對應的頻域數據;
步驟s32b,採用一預設的指數特徵函數組分別與每一維度的頻域數據進行擬合,以得到每一維度的時間離散度特徵分量;
步驟s33b,綜合所有維度的時間離散度特徵分量形成心電動力學數據的時間離散量化特徵。
具體地,本發明的較佳的實施例中,上述步驟s31b中,採用快速傅立葉變化的方法將每一維度的cdvg數據轉換成頻域數據。
具體地,每一維度的cdvg數據可以被表示為:
xi(t),xi∈r1,t=1,2,...,t,i=1,2,3;
經過快速傅立葉變換將上述cdvg數據轉換成頻域信息,可以被表示為:
fi(n),f∈r3,n=1,2,...,n,i=1,2,3。
上述n為採樣頻率。
上述過程中,還包含零頻率點的置零操作,即fi(1)=0,i=1,2,3。
在轉換得到頻域數據之後,採用一預設的指數特徵函數組對每一維度的頻域數據進行擬合,以得到每一維度的時間離散特徵分量。
具體地,上述預設的指數特徵函數組為一類具有特定特徵的指數函數,具體可以為以λ為指數的指數函數,具體可以被表示為fi,λ(n),i=1,2,3。通過指數特徵函數組fi,λ(n)與頻域數據fi(n)進行擬合,並將擬合所用的最優特徵λi參數作為每一維度的時間離散特徵分量。
最後,通過幾何平均的方法把每一維度的時間離散特徵分量λi,i=1,2,綜合形成cdvg數據的時間離散量化特徵,以下述公式計算得到:
本發明的較佳的實施例中,上述步驟s4中,
於一xoy坐標平面中,採用時間離散量化特徵和空間離散量化特徵中的一個作為對應的心電動力學數據的x軸坐標,以及採用時間離散量化特徵和空間離散量化特徵中的另一個作為對應的心電動力學數據的y軸坐標,以形成心電動力學數據的坐標信息;
並且,將坐標信息作為心電動力學數據的量化信息。
具體地,本發明的一個實施例中,於一個xoy坐標平面中,在xy坐標繫上,把x坐標定義為上述時間離散量化特徵(即td指標),同時把y坐標定義為空間離散量化特徵(即sd指標),因此一個cdvg數據具有一個以td指標為x坐標和以sd指標為y坐標的坐標信息(即該cdvg數據的量化信息),則該cdvg數據會對應一個二維空間的分布點來對心電動力學的時空特徵進行表示。
在該情況下,td指標(x坐標)越大則表明cdvg數據的時間周期性越強,即心電動力學數據的時間特徵更趨於周期規整。sd指標(y坐標)越大則表明cdvg數據的空間混沌性越強,即心電動力學數據的空間特徵更趨向於發散混沌。
為了醫生在進行判斷時更加直觀,可以通過作分界線對以xoy坐標平面表示的心電動力學時空特徵分布圖劃分成三個區域(第一區域、第二區域、第三區域)。具體地:
當量化信息表示心電動力學數據落入第一區域中時,表示對應的心電向量圖表示的心臟體徵正常,即該第一區域為陰性區域。
當量化信息表示心電動力學數據落入第二區域中時,表示對應的心電向量圖表示的心臟體徵異常,即該第二區域為陽性區域。
當量化信息表示心電動力學數據落入第三區域中時,表示對應的心電向量圖表示的心臟體徵疑似異常,即該第三區域為可疑陽性區域。
則根據上述td指標和sd指標的特性,若cdvg數據的動態特性越優(即其為規整的環狀結構),那麼td指標就越大並且sd指標越小;若cdvg數據的動態特性越差(即為散亂的空間結構),那麼td指標就越小並且sd指標越大。因此,上述第二區域可以分布在xoy坐標平面的左上方,第一區域可以分布在xoy坐標平面的右下方,其間分布有第三區域。
本發明的另一個實施例中,於一個xoy坐標平面中,在xy坐標繫上,把x坐標定義為上述空間離散量化特徵(即sd指標),同時把y坐標定義為時間離散量化特徵(即td指標),因此一個cdvg數據具有一個以sd指標為x坐標和以td指標為y坐標的坐標信息(即該cdvg數據的量化信息),則該cdvg數據會對應一個二維空間的分布點來對心電動力學的時空特徵進行表示。針對上述cdvg數據的量化信息的分析以及相應判斷區域的劃分可以比照上文中所述進行處理,在此不再贅述。
下文中所述為本發明的一個較佳的實施例中對cdvg數據做量化分析以驗證本發明技術方案的具體過程:
本實施例中選取ptb數據中提供的心肌梗塞數據p065為例。
本實施例中,首先根據p065心肌梗塞的心電數據採用確定學習動力學建模生成cdvg數據xt(如圖6中所示),隨後對該cdvg數據提取時間離散量化特徵和空間離散量化特徵。
在提取空間離散量化特徵時,首先在第一個點xk,k=1處執行尋找當前軌跡點的臨近點集的步驟。本實施例中,上述a1可以取值30,即上述臨近點集中包括30個數據點,隨後根據上述公式(1)計算得到初始距離集合。隨後根據上述公式(2)計算得到結束距離集合。本實施例中,在應用上述公式(2)時,可以取值δ=10。本實施例中,隨後,採用以2為底的對數函數找到非負的指數增長係數集(即指數變化率)並根據上文中所述的方法計算得到空間離散度係數。最後進行cdvg數據長度為t的循環運算,以求得所有時間點的空間離散度係數,並且通過平均運算作為cdvg數據的空間離散量化特徵(即sd指標)。例如,採用上述心肌梗塞數據p065經過計算後可以求得其sd指標sd=3.0691。
在提取時間離散量化特徵之前,需要進行數據預處理的操作,即通過快速傅立葉變換方法分別將每一維度的cdvg數據轉化成頻域數據。由於在轉化過程中,部分數據的零頻率點會發生較大的偏移,因此進行零頻率點的置零操作以解決該偏移問題。隨後,採用預設的特徵函數組與頻域數據進行擬合,並將擬合所用的最優特徵參數作為分別對應每一維度的數據的時間離散特徵分量。最後,通過幾何平均的方法將每一維度的時間離散特徵分量綜合形成cdvg數據的時間離散量化特徵(即td指標)。例如上述心肌梗塞數據p065,其經過計算後可得到td指標td=42.4774。
得到了cdvg數據的sd指標和td指標後,就可以以xoy坐標信息的方式形成該cdvg數據的量化信息。例如將sd指標作為x軸坐標,將td指標作為y軸坐標,則上述量化信息可以被表示為(3.0691,42.4774),即表示cdvg數據在xoy坐標平面表示的二維平面中的分布點位置。又例如將sd指標作為y軸坐標,將td指標作為x軸坐標,則上述量化信息可以被表示為(42.4774,3.0691)。
最後,根據該量化信息可以對cdvg數據進行判斷。具體地,如圖7所示,以td指標作為x軸坐標,sd指標作為y軸坐標為例,在xoy坐標平面中劃分了第一區域a,第二區域b以及第三區域c。其中第一區域a為陰性區域,第二區域b為陽性區域,第三區域c為可疑陽性區域。而上述心肌梗塞數據p065的量化信息(a點)顯示其落在第二區域b內,且距離分界線較遠,因此認為該cdvg數據顯示患者具有心肌缺血的危險。
最後根據心肌梗塞數據p065在ptb資料庫中的病歷信息顯示,患者死於心肌梗死,並且其cdvg圖如圖6所示,顯示為略顯散亂的環狀。這與最終量化信息的分析結果均相符合,因此完成對本發明技術方案的驗證。
以上所述僅為本發明較佳的實施例,並非因此限制本發明的實施方式及保護範圍,對於本領域技術人員而言,應當能夠意識到凡運用本發明說明書及圖示內容所作出的等同替換和顯而易見的變化所得到的方案,均應當包含在本發明的保護範圍內。
