一種數據聚類方法及裝置與流程

2023-05-07 11:57:07 1

本申請涉及數據分析
技術領域：
，尤其涉及一種數據聚類方法及裝置。
背景技術：
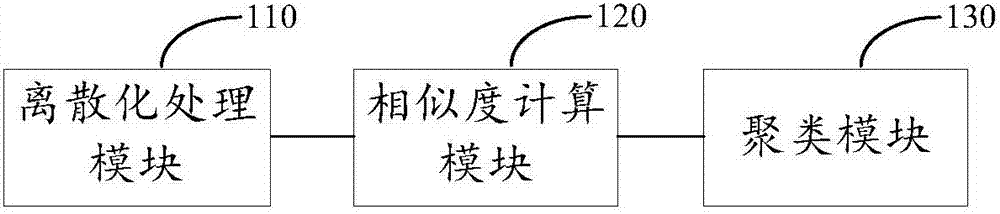
：數據分析是指用適當的統計方法對數據集合進行分析，從而提取有用信息和形成結論的過程。在大數據時代，如何從海量的信息數據中更有效地提取出有用信息已經成為一個重點研究課題。數據分析的一種實際應用需求是：根據數據的特徵，從大量數據對應的實體中篩選出一些異常的實體，而這些異常實體往往會存在一定的意義，例如：通過對不同終端對伺服器的訪問行為數據進行篩選，可以從大量終端中識別出具有網絡攻擊行為的終端；通過對不同商戶的交易行為數據進行篩選，可以從大量商戶中識別出一些優質商戶；等等。在數據篩選的初始階段，篩選的標準往往是不確定的，有時甚至連篩選的目的都不明確，在這種需求背景下，聚類成為數據篩選的重要手段，在具體篩選標準不明確的情況下，聚類結果往往能夠直接滿足篩選需求，或者為數據分析人員提供重要的指導意義。目前，聚類算法有很多種，例如kmeans、dbscan、譜聚類、som等等，但是這些聚類算法均要求數據樣本之間的距離是可度量的，而在實際的數據分析過程中，一條信息數據可能包含多種類型的特徵屬性，例如數值類、布爾類、文本類、時間類等等。應用現有的聚類算法，需要對各類特徵屬性取值的距離進行統一定義，如果定義不合適則需要反覆調整，特徵的數量、種類越多，調整的工作量就越大。對於數據分析人員而言，調整定義特徵屬性的取值距離往往需要消耗大量的時間和精力成本，這也對整體的數據篩選處理效率造成了較大的影響。技術實現要素：針對上述技術問題，本申請提供一種數據聚類方法及裝置，技術方案如下：根據本申請的第一方面，提供一種數據聚類方法，該方法包括：對待處理數據樣本集的連續變量特徵取值進行離散化處理；根據離散化處理結果，利用預設的相似度算法計算任意兩個數據樣本i和j之間的相似度sij(i≠j)，其中i、j的取值包括不大於n的所有自然數，n為所述數據樣本集中的數據樣本總數；根據任意兩個數據樣本i和j之間的相似度sij，利用預設的聚類算法對所述n個數據樣本進行聚類。根據本申請的第二方面，提供一種數據聚類裝置，該裝置包括：離散化處理模塊，用於對待處理數據樣本集的連續變量特徵取值進行離散化處理；相似度計算模塊，用於根據離散化處理結果，利用預設的相似度算法計算任意兩個數據樣本i和j之間的相似度sij(i≠j)，其中i、j的取值包括不大於n的所有自然數，n為所述數據樣本集中的數據樣本總數；聚類模塊，用於根據任意兩個數據樣本i和j之間的相似度sij，利用預設的聚類算法對所述n個數據樣本進行聚類。應用本申請所提供的技術方案，在對數據集進行聚類時，僅考慮特徵的取值的離散性，無需考慮數據各個特徵的具體類型，對於連續變量特徵，通過對其特徵取值進行離散化處理，使其與離散變量特徵能夠採用統一的標準進行度量，因此本申請方案對於任意的信息數據集，無論有多少個特徵，特徵的具體類型如何，均能夠自動計算出數據樣本的距離並進行聚類，從而有效地降低數據篩選過程中的聚類調試成本消耗，提高數據篩選的處理效率。應當理解的是，以上的一般描述和後文的細節描述僅是示例性和解釋性的，並不能限制本申請。附圖說明為了更清楚地說明本申請實施例或現有技術中的技術方案，下面將對實施例或現有技術描述中所需要使用的附圖作簡單地介紹，顯而易見地，下面描述中的附圖僅僅是本申請中記載的一些實施例，對於本領域普通技術人員來講，還可以根據這些附圖獲得其他的附圖。圖1是本申請的數據聚類方法的流程示意圖；圖2是本申請的數據聚類裝置的結構示意圖。具體實施方式為了使本領域技術人員更好地理解本申請中的技術方案，下面將結合本申請實施例中的附圖，對本申請實施例中的技術方案進行詳細地描述，顯然，所描述的實施例僅僅是本申請一部分實施例，而不是全部的實施例。基於本申請中的實施例，本領域普通技術人員所獲得的所有其他實施例，都應當屬於本申請保護的範圍。圖1所示，為本申請提供的數據聚類方法的流程圖，該方法可以包括以下步驟：s101，對待處理數據樣本集的連續變量特徵取值進行離散化處理；對於一個待處理的數據樣本集，可能包含多種類型的特徵，例如數值類、布爾類、文本類、時間類等等，根據現有技術方案，為了對數據樣本進行聚類，需要對各類特徵屬性取值的距離進行統一定義，而如何選取合適的定義標準則是一個需要消耗大量嘗試成本的步驟。針對該問題，本申請提供的方案是：不考慮特徵的具體類型，僅考慮特徵的取值的離散性。由於相對於連續變量特徵而言，離散變量特徵的取值數量是有限的，更便於在同一特徵的維度上度量兩個樣本之間的相似性。因此對於數據樣本中取值為連續變量的特徵，對其取值進行離散化處理，使其與離散變量特徵能夠採用統一的標準進行度量。假設數據樣本集中的數據樣本總數為n、且數據樣本共有l個特徵，其中連續變量特徵的數量為l1、離散特徵的數量為l2，即l＝l1+l2。則對於l1個連續變量特徵中的任一個特徵，都具有n個取值。離散化的過程就是根據一定的算法，將這個n個取值劃分k(k＜n)個離散區間，並為每個離散區間指定一個對應的離散取值。對特徵取值的離散化處理，可以採用現有的離散化算法，例如kmeans、dbscan、som等聚類算法，都可以用於離散化處理。在具體應用中，還可以通過最優參數算法來自動計算聚類算法中所需要的參數值，例如kmeans算法中的k值等，從而進一步降低數據處理人員的調試成本s102，根據離散化處理結果，計算任意兩個數據樣本i和j之間的相似度；對連續變量特徵進行離散化處理後，原本大量的連續取值變為少量的離散取值，也使得數據樣本集的l個特徵都統一為離散變量特徵，從而便於進一步計算數據樣本之間的相似度。對於離散取值的樣本的相似度計算，可以採用現有的相似度計算方法。為便於實現，在本申請的一種實施方式中，對於任意兩個數據樣本i和j(i＝1,2,3…n；j＝1,2,3…n)，可以先計算i和j之間的樣本距離dij，然後將dij轉換為i和j之間的樣本相似度sij。其中，樣本距離可以採用漢明距離、歐式距離等多種方式進行計算，而將距離轉換為相似度也可以通過不同的方法實現，例如直接對距離值取倒數得到相似度(即sij＝1/dij)，或對距離值的對數取倒數得到相似度(即sij＝1/logdij)，等等，本申請對這些具體的算法的選擇均不需要進行限定。s103，根據任意兩個數據樣本i和j之間的相似度sij，利用預設的聚類算法對n個數據樣本進行聚類。其中，聚類結果中的一個或多個類簇可以用於形成對所述數據樣本集的數據篩選結果。得到任意兩個數據樣本i和j的樣本相似度sij後，可以生成相應的相似度圖，該相似度圖具有n個頂點，分別對應n個數據樣本，任意兩個頂點i和j之間存在一條以sij為權重值的邊。利用基於圖分割的聚類算法對上述生成的相似度圖進行聚類，這裡可以採用譜聚類、標籤傳播聚類、fastunfolding等聚類算法。其中標準譜聚類方式在理論上較為嚴謹，當數據樣本的數量n較大時，可以選用時間複雜度稍低的近似譜聚類算法poweriterationclustering進行聚類。當然，本申請方案並不限定必須使用基於圖分割的距離算法，例如，在分布式計算環境下，可以採用svd矩陣分解得到數據樣本相似度矩陣的特徵向量，並對特徵向量進行kmeans聚類得到每個樣本所屬的類別。得到聚類結果後，可以根據聚類數量、聚類的相對大小等具體情況進行數據篩選。例如，在篩選異常數據時，可以優先關注聚類結果中較小的類簇，當然，根據不同的應用需求，聚類結果中的每一個類簇都可能成為對原數據樣本集的數據篩選結果，具體的篩選原則與本申請方案無關，這裡不做詳細介紹。下面將結合一個具體的實例，對本申請方案進行說明假設待處理的數據樣本集如表1所示：agecitydepositmarriage110上海1000.00225南京2000.01311上海3000.00436北京4000.01524北京5000.02626北京6000.01表1該數據樣本集包含的樣本數n＝6，特徵數l＝4，分別為age、city、deposit、marriage，其中age和deposit是連續變量特徵，根據s101，首先對連續變量的取值進行離散化處理。在本實施例中，選用常見的kmeans算法對連續變量特徵的取值進行離散化處理。kmeans本身也是一種聚類算法，其接收輸入參數k，然後將n個數據對象劃分為k個聚類以便使得所獲得的聚類滿足：同一聚類中的對象相似度較高；而不同聚類中的對象相似度較小。假設數據樣本集中的數據樣本總數為n，則對於數據樣本集中的任意連續化特徵，可以將離散化問題轉換為對n個數據樣本的該特徵取值進行聚類。為了實現自適應離散化處理，kmeans算法中的k值可以利用最佳聚類數算法確定。目前用於檢驗聚類有效性的指標主要有calinski-harabasz(ch)指標、davies-bouldin(db)指標、krzanowski-lai(kl)指標等等。本實施例中利用ch指標自動計算最優的k值，ch的表達式如下：其中n為數據樣本的總數，l表示第l個連續變量特徵，用于衡量第l個連續變量特徵，在被分割為k個類後，k個類的類間距離和；用于衡量第l個連續變量特徵，在被分割為k個類後，k個類的類內距離和，其中距離的具體衡量算法可以是距離加和、歐式距離等，本申請不做限定。對於第l個連續變量特徵，選取能夠令值最大的k值作為最優解。利用上述方法，可得到特徵age和deposit的離散化結果如下：特徵age的最佳k值為3，對應的離散區間為(9,20]、(20,24]、(24,36]，分別為其指定對應的離散取值0、1、2；特徵deposit的最佳k值為2，對應的離散區間為(1000.0,3000.0]、(3000.0,6000.0]，分別為其指定對應的離散取值0、1；離散化處理之後，可以將表1所示的數據樣本集轉換成如表2所示的全離散值的數據樣本集：agecitydepositmarriage10上海0022南京0130上海0042北京1151北京1262北京11表2根據s102，對於數據樣本集d1，分別計算任意兩個數據樣本i和j之間的相似度sij。在本實施例中，採用修正的漢明距離算法計算任意兩個樣本點之間的距離dij，然後利用高斯核函數將dij轉換為樣本間相似度sij，其中，對於任意兩個數據樣本i和j(i＝1,2,...n、j＝1,2,...n)，其樣本間相似度的具體計算過程如下：首先分別計算i的第l個特徵值和j的第l個特徵值的距離dl(i,j)，經過離散化處理後，這裡可以採用漢明距離的計算思想：如果兩個特徵值相等，則距離為0，如果兩個特徵值不相等，則距離為1。例如，對於表2中的第1條數據和第2條數據，age特徵的距離為1、city特徵的距離為1、deposit特徵的距離為0、marriage特徵的距離為1。遍歷所有的l(從1到l)，得到所有的dl(i,j)後，對l個dl(i,j)進行求和，得到i和j的距離dij:在有些情況下，不同的特徵對應的離散區間數量相差較大，為了平衡這種差別，可以通過加權的方式對各個特徵的距離進行修正。加權的基本思想是：某個特徵對應的離散區間數量大，該特徵內兩個不同的取值所體系出的距離應該越小。實際應用中，每項dl(i,j)可以以1/kl作為權值，當然也可以使用kl的指數冪的倒數或對數的倒數等作為權值，本申請對此並不需要進行限定。在本申請的一種實施方式中，對每個dl(i,j)增加修正參數1/kl，其中kl為數據樣本第l個特徵所對應的離散區間數量，得到修正的樣本間距離計算公式如下：針對表2所示的數據樣本集，利用上述修正距離計算公式，可以得到樣本間距離矩陣如表3所示：表3表3所示矩陣中，第i行第j列的數值即為i和j的距離dij，可以看出該矩陣為對稱矩陣，即dij＝dji。進一步，利用高斯核函數，將任意兩個樣本i和j的之間距離dij轉換為任意兩個樣本i和j之間的相似度sij，高斯核函數也稱徑向基函數，表達式如下：其中ε為高斯半徑，是可以自定義的參數，將距離轉換為相似度的目的，在於將距離較為稠密的樣本點稀疏化，使得在一個樣本點x周圍，如果其他樣本點y與x的距離超過了ε，則x與y的相似度能夠明顯衰減。為了實現自適應處理，這裡ε可以取值為所有數據樣本對之間距離的標準差，當然這並不應理解為對本申請方案的限定，本領域技術人員可以根據實際情況(例如採用多次嘗試法)選取具體的ε值。針對表3所示的樣本間距離矩陣，利用高斯核函數進行轉化後，可以得到如表4所示的樣本間相似度矩陣：表4表4所示矩陣中，第i行第j列的數值即為i和j的相似度sij，可以看出該矩陣為對稱矩陣，即sij＝sji。最後，根據s103，對數據樣本集進行聚類。首先根據sij構成的樣本點相似度圖，該相似度圖具有6個頂點，分別對應6個數據樣本，任意兩個頂點i和j之間存在一條以sij為權重值的邊，利用標準譜聚類算法得到最終聚類結果如表5所示：agecitydepositmarriagecluster110上海1000.001225南京2000.012311上海3000.002436北京4000.012524北京5000.022626北京6000.012表5可見，數據樣本2、3、4、5、6屬於一個類簇，數據樣本1則屬於另外一個類簇，從數據分析的角度，可以認為樣本1存在異常，並將樣本1篩選出來以作後續的分析處理。可見，應用上述技術方案，無論給定數據樣本集包括多少個特徵、特徵的具體類型如何，均能夠自動計算出數據樣本的距離並進行聚類，從而有效地降低數據篩選過程中的聚類調試成本消耗。在本申請方案改進的實施方式中，通過自適應確定參數等手段，還可以進一步減少數據分析人員的參數調試工作，使聚類過程不需要任何人工參與，只要輸入數據樣本集就可以自動得出最優的聚類結果，從而有效提高數據篩選的整體處理效率。相應於上述方法實施例，本申請還提供一種數據聚類裝置，參見圖2所示，該裝置可以包括：離散化處理模塊110，用於對待處理數據樣本集的連續變量特徵取值進行離散化處理；相似度計算模塊120，用於根據離散化處理結果，利用預設的相似度算法計算任意兩個數據樣本i和j之間的相似度sij(i≠j)，其中i、j的取值包括不大於n的所有自然數，n為數據樣本集中的數據樣本總數；聚類模塊130，用於根據任意兩個數據樣本i和j之間的相似度sij，利用預設的聚類算法對n個數據樣本進行聚類。在本申請的一種具體實施方式中，離散化處理模塊110可以具體用於：對於任一連續變量特徵，利用kmeans算法對n個數據樣本的該特徵取值進行聚類，並為每個類簇指定相應的離散取值。其中，kmeans算法的k值可以利用最佳聚類數算法自動確定。在本申請的一種具體實施方式中，相似度計算模塊120可以具體用於：對於任意兩個數據樣本i和j：分別計算i的第l個特徵值和j的第l個特徵值的距離dl(i,j)，其中l的取值包括不大於l的所有自然數，l為數據樣本的特徵總數；對l個dl(i,j)進行求和得到i和j的距離dij；利用高斯核函數計算sij，ε為預設的高斯半徑參數。在本申請的一種具體實施方式中，相似度計算模塊120可以利用對l個dl(i,j)進行加權求和的方式得到i和j的距離dij；其中加權求和的權值為1/kl，kl為數據樣本第l個特徵所對應的離散區間數量。在本申請的一種具體實施方式中，ε的取值可以是所有數據樣本對之間距離的標準差。通過以上的實施方式的描述可知，本領域的技術人員可以清楚地了解到本申請可藉助軟體加必需的通用硬體平臺的方式來實現。基於這樣的理解，本申請的技術方案本質上或者說對現有技術做出貢獻的部分可以以軟體產品的形式體現出來，該計算機軟體產品可以存儲在存儲介質中，如rom/ram、磁碟、光碟等，包括若干指令用以使得一臺計算機設備(可以是個人計算機，伺服器，或者網絡設備等)執行本申請各個實施例或者實施例的某些部分所述的方法。本說明書中的各個實施例均採用遞進的方式描述，各個實施例之間相同相似的部分互相參見即可，每個實施例重點說明的都是與其他實施例的不同之處。尤其，對於裝置實施例而言，由於其基本相似於方法實施例，所以描述得比較簡單，相關之處參見方法實施例的部分說明即可。以上所描述的裝置實施例僅僅是示意性的，其中所述作為分離部件說明的模塊可以是或者也可以不是物理上分開的，在實施本申請方案時可以把各模塊的功能在同一個或多個軟體和/或硬體中實現。也可以根據實際的需要選擇其中的部分或者全部模塊來實現本實施例方案的目的。本領域普通技術人員在不付出創造性勞動的情況下，即可以理解並實施。以上所述僅是本申請的具體實施方式，應當指出，對於本
技術領域：
的普通技術人員來說，在不脫離本申請原理的前提下，還可以做出若干改進和潤飾，這些改進和潤飾也應視為本申請的保護範圍。當前第1頁12