基於倍四元數的工業機器人自由曲線的軌跡規劃控制方法與流程

2023-04-26 18:20:31

本發明涉及一種基於倍四元數的工業機器人自由曲線的軌跡規劃控制方法，屬於機器人軌跡規劃技術領域。

背景技術：
現代製造業對機器人性能的要求也越來越高，而機器人在任務空間的軌跡規划算法在機器人控制系統中佔有重要地位，直接影響著機器人末端運動性能和效率。且機器人運動控制中，基本的直線、圓弧軌跡曲線已不能滿足工業加工的應用需求，而常用的B樣條曲線、Bézier曲線、Clothoid曲線，均不能用一種精確統一的表示方法描述標準解析曲線和自由曲線。通常情況下，機器人的期望軌跡是事先給定一系列笛卡爾或者關節空間的點，且給定通過該點的速度或兩點間的時間，另外還會限制機器人運動允許的最大速度，繼而分別實現機器人末端執行器的位置軌跡規劃和姿態軌跡規劃，而工業機器人姿態軌跡規劃通常採用歐拉角法、等效軸法對姿態進行插補，但歐拉角存在萬向死鎖的缺陷，等效軸法在旋轉量為0時存在無法確定旋轉軸的問題。雖然使用四元數法可解決機器人姿態軌跡插補的上述問題，但軌跡的位置插補則需使用其它的插補算法，運算量大，影響控制系統對軌跡規劃的實時性要求。

技術實現要素：
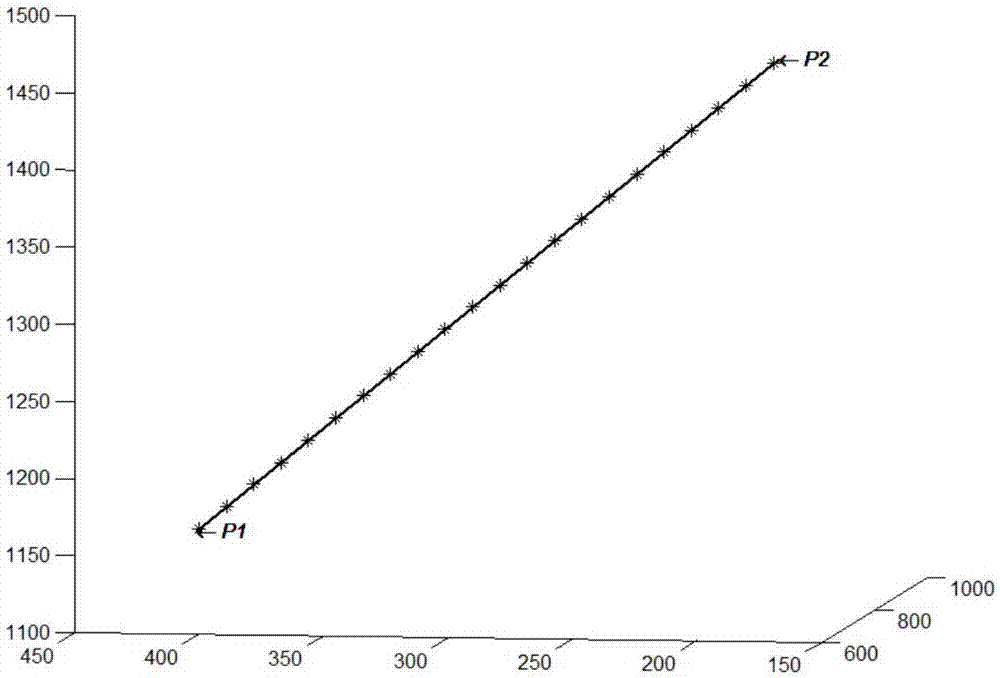
本發明所要解決的技術問題是克服現有技術的缺陷，提供一種基於倍四元數的工業機器人NURBS曲線軌跡規劃控制方法，能夠為工業機器人實現自由曲線軌跡規劃提供一種高效、高精度的控制方法。為解決上述技術問題，本發明採用的技術方案如下：基於倍四元數的工業機器人自由曲線的軌跡規劃控制方法，包括以下步驟：1)建立基於倍四元數的機器人末端執行器空間位姿的數學模型與機器人末端執行器在任務空間NURBS描述的自由曲線數學模型；2)給定機器人末端執行器在任務空間NURBS描述的自由曲線的控制點序列D，以及控制點對應姿態R；所述控制點序列D表示為：D＝{d0，d1，…，dn}，n為控制點個數；所述控制點對應姿態採用姿態旋轉矩陣R3×3表示；3)依據哈特利-賈德法求解所述步驟2)的控制點序列中控制點對應的節點矢量U，具體過程如下：為給定的控制點di，i＝0,1,…,n，預定義一條k次非均勻有理B樣條曲線，同時確定它的節點矢量U＝[u0,u1,…,un+k+1]中的具體的節點值，節點值的求解如下：將兩端節點的重複度取為k+1，將曲線的定義域取成規範參數域，即u∈[uk,un+1]＝[0,1]，於是u0＝u1＝…＝uk＝0，un+1＝un+2＝…＝un+k+1＝1，其餘節點值需計算求解，如下：計算公式如下：式中，lj為控制多邊形的各邊長，lj＝|dj-dj-1|，由式(4)可得：繼而可得所有的節點值；其中，u為節點矢量U相鄰兩個節點間的密化節點值，ui，i＝0,1,……,n+k+1，表示節點矢量U中具體的某個節點值；4)依據Adams微分方程理論算法對節點矢量U進行密化處理，具體過程如下：採用三步四階Adams微分方程的隱格式表示為：其中，T為插補周期，分別為ui-2、ui-1、ui、ui+1的一階導數；將代入上式，可得：ΔLi表示控制點di的進給步長；採用前、後向差分結合代替微分的方法進行簡化：後向差分，前向差分，前向差分，前向差分將上式代入式(7)，得到：進而得到簡化後的Adams微分方程插補算法迭代公式：繼而可得密化後節點矢量，其中，表示ui+1的預估值；5)根據步驟1)中的機器人末端執行器空間位姿的數學模型，並採用自適應速度控制算法對密化後的節點矢量進行修正處理，最終獲得最優的密化節點矢量，修正處理過程如下：將參數作為參數插補的預估值代入NURBS方程，得到相對應的預估插補點：表示預估值的預估插補點，從而得到對應的預估進給步長為：預估進給步長和進給步長ΔLi之間存在的偏差，用相對誤差δi來表示：當相對誤差δi在允許範圍內時，則為所求p(ui+1)，否則按下式進行修正，直至達到δi允許範圍內：最終獲得最優的密化節點矢量；6)利用步驟5)的最優的密化節點矢量，並根據步驟1)中機器人末端執行器在任務空間NURBS描述的自由曲線數學模型，最終獲得曲線上的插補點位置；7)根據相鄰空間曲線的插補點位置與姿態數據，進行倍四元數轉換，具體步驟如下：7-1)對於每一個機器人末端位姿齊次變換矩陣BTE，如下所示：首先將姿態旋轉矩陣R3×3，經旋轉矩陣與四元數的轉換關係，得到姿態旋轉矩陣對應的旋轉四元數Q，同時獲得平移向量P＝[px(u),py(u),pz(u)]T；7-2)將三維空間的平移向量P轉換成四維空間的四元數，轉換公式如下：Dp＝cos(ψ/2)+sin(ψ/2)v(16)式中，Rl為四維空間的大球半徑，ψ＝|P|/Rl，v是平移向量上的單位矢量，v＝P/|P|；當|P|＝0時，v為零矢量；7-3)通過以下公式，計算得到機器人末端位姿轉換至四維空間的倍四元數空間位姿的G部和H部；式中，為四元數Dp的共軛；7-4)倍四元數的雙旋轉軌跡進行離散化得到一系列插值倍四元數點，需要將其轉換成旋轉四元數和平移向量，轉換算法如下：Q＝(G+H)/(2cosψ)(17)式中，8)對插補所得機器人末端執行器位姿進行逆運動學處理，獲得關節角度，並驅動關節運動。前述的步驟1)中，基於倍四元數的機器人末端執行器空間位姿的數學模型為：其中，表示機器人末端執行器倍四元數空間位姿，ξ和η滿足ξ2＝ξ，η2＝η，ξ+η＝1，ξη＝0，G和H均為單位四元數；機器人末端執行器在任務空間NURBS描述的自由曲線數學模型為：任意一條k次NURBS曲線均表示為一分段有理多項式矢函數：其中，p(u)表示機器人末端執行器在任務空間NURBS描述的自由曲線的位置矢量，ωi稱為權因子；di為自由曲線控制點；n為控制點個數；Ni,k(u)是由節點矢量U＝[u0,u1,…,un+k+1]決定的B樣條基函數，由德布爾-考克斯遞推定義公式表示：式中，規定u為節點矢量U相鄰兩個節點間的密化節點值，ui，i＝0,1,……,n+k+1，表示節點矢量U中具體的某個節點值。本發明所達到的有益效果：本發明能夠為實現工業機器人在笛卡爾空間的NURBS自由曲線的軌跡規劃，提供一種有效提高工業機器人的工作效率和工作質量、能夠減小速度波動、改善機器人的工作環境的控制方法。附圖說明圖1為本發明基於倍四元數的工業機器人自由曲線的軌跡規劃控制方法流程示意圖；圖2為本發明基於倍四元數的工業機器人自由曲線的軌跡規劃控制方法的倍四元數表述空間直線段位置的示意圖；圖3為本發明基於倍四元數的工業機器人自由曲線的軌跡規劃控制方法的倍四元數表述空間直線段姿態的示意圖，圖中箭頭方向為姿態用四元數表示的旋轉矢量軸。具體實施方式下面結合附圖對本發明作進一步描述。以下實施例僅用於更加清楚地說明本發明的技術方案，而不能以此來限制本發明的保護範圍。自由曲線概念的提出就是為了描述比較複雜的幾何形狀，以提高工業機器人的加工效率和精度。而非均勻有理B樣條(NURBS，Non-UniformRationalB-Spline)曲線，可以準確的透視出曲線造型的控制點分布特徵，並可以有效的解決型值點不能均勻分布的缺點。倍四元數是基於Clifford代數的一種新的數學建模工具，是在四元數的基礎上發展而來。採用倍四元數能夠對笛卡爾空間中的位置與姿態轉換至四維空間中，既能夠分別得表示空間中的位置和姿態，也能將空間中的位置和姿態用一種統一的方式進行表示，從而對四維空間中起止點的位姿用超球面旋轉對機器人的運動軌跡進行球面線性插補。如圖1所示，本發明的基於倍四元數的工業機器人自由曲線的...