一種腦功能連接分析的稀疏貝葉斯網絡與Granger雙約束方法與流程

2023-08-01 05:09:16 2

本發明涉及fmri數據的功能網絡連接分析，特別是涉及一種腦功能連接分析的稀疏貝葉斯網絡與granger雙約束方法。

背景技術：

功能磁共振成像(functionalmagneticresonanceimaging，fmri)是一種神經影像學技術，具有高空間解析度、可重複檢測、無創傷性等優點，已成為腦功能研究和腦疾病診斷的重要工具之一。數據驅動的獨立成分分析(independentcomponentanalysis,ica)方法能夠從fmri數據中提取出被試(subject)的腦空間激活區(spatialmap,sm)成分及其對應的時間過程(timecourse,tc)成分。基於tc成分進行的腦功能連接(functionalconnectivity)分析，可探究不同腦區之間相互作用與協調的模式，發現腦疾病(如精神分裂症、阿爾茲海默病、抑鬱症、躁鬱症等)患者與健康對照被試在腦功能連接方面的顯著異常，進而用於腦疾病研究與輔助診斷。

功能連接分為無向的功能連接及有向的功能連接。其中，無向的功能連接簡稱功能連接，強調的是不同腦區之間的相關性。有向的功能連接又稱為有效連接(effectiveconnectivity)或因果連接，強調的是兩個腦區之間的因果關係。格蘭傑因果分析(grangercausalityanalysis，簡稱granger)和稀疏貝葉斯網絡(sparsebayesiannetwork,sbn)是兩種有效連接分析方法。granger方法採用的是多元自回歸模型，根據兩個時間序列的過去值對現在值的預測結果，判斷兩者之間的granger因果關係(見c.w.j.granger,investigatingcausalrelationsbyeconometricmodelsandcross-spectralmethods,econometrica37(3):424-4381969)。假設xt和yt為兩個零均值的平穩時間序列，那麼因果模型可以表示為

其中，ap，bp，cp和dp為自回歸參數，εt和ηt是兩個零均值不相關的白噪聲序列，e[εt]＝0，e[ηt]＝0，且

xt和yt使用其過去的m個值進行預測，m也可以理解為自回歸模型的階數。如果使用了時間序列yt的過去值yt-j,j＝1,…,m去預測時間序列xt，比僅僅使用xt的過去值xt-j,j＝1,…,m去預測時間序列xt的噪聲方差更小，則可以說yt是xt的granger原因；反之亦然。

貝葉斯網絡(bayesiannetwork,bn)是一種基於圖論和概率論的數學模型，通過一些變量的信息來推斷其它變量的概率信息，適於分析多變量間具有不確定性的複雜關係，已廣泛應用於遺傳學、生態學、社會科學和腦科學等領域。bn結構是一個有向無環圖(directedacyclicgraph,dag)，由代表隨機變量的節點及連接這些節點的有向邊(由父節點指向其子節點)構成，表示了各變量之間的依賴或獨立關係。huang等人提出了一種sbn結構學習算法(huangs,lij,yej,etal.,asparsestructurelearningalgorithmforgaussianbayesiannetworkidentificationfromhigh-dimensionaldata,ieeetransactionsonpatternanalysisandmachineintelligence,2013,35(6):1328-1342.)。其基本做法是，增加了一項l1範數懲罰項以施加連接的稀疏性約束；同時增加了另一項懲罰項以保障bn是一個有向無環圖。稀疏約束可以有效地減少bn結構學習的計算量，同時sbn將傳統bn結構的兩步學習(先確定每個節點可能的父節點，再從中識別最終的父節點)簡化為一步學習，即直接確定所有變量的父節點，降低了丟失父節點的可能，提高了結構學習的精度。理論分析和實驗測試結果均表明，sbn結構學習算法較之現有十種bn結構學習算法在精度和效率方面均有提升。

對於同一種fmri數據，不同分析方法所檢測的腦功能連接應該既有區別又有聯繫。然而，在現有腦功能連接分析中，各種方法的分析大多彼此獨立，導致不同方法的分析結果也相互獨立，難於比較；而且，sbn方法尚未用於fmri數據的腦功能連接分析。因此，進行sbn和granger兩種方法的聯合分析，挖掘二者之間的內在聯繫，提取魯棒而穩定的腦功能連接，對深入推進腦功能研究和腦疾病診斷極為重要。

技術實現要素：

本發明的目的在於，提供一種對fmri數據聯合進行sbn與granger有效連接分析的方法，揭示兩種方法檢測結果之間的內在聯繫，提取穩定的腦網絡連接。

本發明的技術方案是，對於從多被試fmri數據中提取的tc成分，同時進行sbn分析與granger因果連接分析。通過對sbn分析方法施加回歸係數約束，以及對granger因果連接分析方法施加因果一致性(causalitycoherence)約束，因果一致性也就是因果性強度，尋找兩種有效連接方法間的內在一致性，提取兩種方法共有的網絡連接，作為多被試fmri數據的穩定腦功能連接加以輸出。

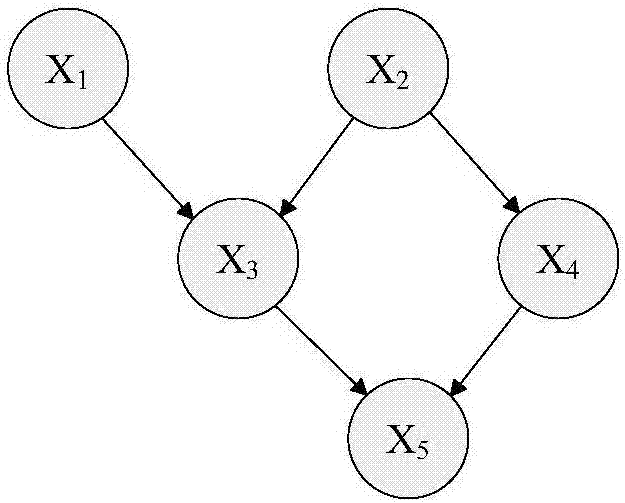
對於一個有p個節點的bn(圖1中的bn有5個節點)，這裡用一個p×p矩陣g來表示其結構。gij＝1表示節點xi到xj有一個有向弧，xi是xj的父節點；gij＝0表示節點xi到xj無連接。另外，用一個p×p矩陣p來表示bn的有向路徑，如果節點xi到xj有一個有向路徑，則pij＝1，反之則為0。如果節點x1是節點x2的父節點，且節點x2是節點x3的父節點，那麼p13＝1，而g13＝0。

當每個節點都滿足多元正態分布時，節點xi可用下面公式(5)中的回歸係數模型來表示：

其中，t(xi)表示節點xi所有父節點的集合；εi為高斯白噪聲，均值為0，方差為βi＝(β1i,…,βpi)t是節點xi的回歸係數向量，βij∈(0,1)，j＝1,…,p；b＝[β1,…,βp]表示回歸係數矩陣。

sbn方法通過學習回歸係數矩陣b，達到確定bn結構的目的。βi非零元素越少，則bn連接越稀疏。huang等人證明，對於一對節點xi和xj，dag的充分必要條件是βij×pji＝0。所以，sbn方法的目標函數如公式(6)所示：

其中，表示節點xj屬於集合x/i(此節點集中不包含xi)，即xj是與xi不同的節點；λ1為稀疏約束參數，λ2為dag約束參數。sbn方法的實現流程如圖2所示，具體步驟如下：

步驟1，輸入包含p個節點數據的數據矩陣x∈rp×n，停機參數ε，以及約束參數λ1，λ2；λ2>(n-1)2p/λ1-λ1，n為每個節點數據的長度。λ1可根據對稀疏性的要求設定，λ1越大則bn結構越稀疏；ε可根據對結果精度的要求設置，ε越小精度越高；

步驟2，初始化結構矩陣g∈rp×p，沒有先驗結構信息時，令g＝0；有先驗結構信息時，若節點i到節點j有一個有向弧，則gij＝1，反之gij＝0；初始化回歸係數矩陣b＝[β1,…,βp]∈rp×p，βi＝(β1i,…,βpi)t，i＝1,…,p，令b＝0；

步驟3，令迭代次數k＝0；

步驟4，對於回歸係數矩陣b，設置當前學習列數i＝1；

步驟5，對結構矩陣g進行廣度優先搜索，得到有向路徑矩陣p：如果節點i到j有一個有向路徑，則pij＝1，反之則pij＝0；

步驟6，對回歸係數矩陣b第i列βi(k)的每個元素進行學習，得到βi(k+1)：設置當前學習元素j＝1；

步驟7，利用公式(7)學習得到βi(k+1)中的第j個元素

其中x/(i,j)表示不包含第i個節點和第j個節點數據的數據矩陣x，βi/j表示不包含第j個元素的第i列回歸係數βi；

步驟8，判斷j是否小於p，若是，則j＝j+1，並跳轉到步驟7；若否，則跳轉到步驟9；

步驟9，應用βi(k+1)更新g矩陣：如果那麼令gji＝1；

步驟10，判斷i是否小於p，若是，則i＝i+1，並跳轉到步驟5；若否，則跳轉到步驟11；

步驟11，判斷||bk+1-bk||2是否小於ε，若否，則k＝k+1，並跳轉到步驟4；若是，則跳轉到步驟12；

步驟12，輸出最終的結構矩陣gnew、回歸係數矩陣bnew。

本發明雙約束分析的具體步驟如下：

第一步，輸入從k個被試fmri數據中分別提取的tc成分，記為x′(k)∈rl×t,k＝1,…,k，l為tc成分的個數，t為tc成分的時間點數；

第二步，採用截止頻率為fl～fh(單位hz)的帶通濾波器對x′(k)進行濾波，得到濾波後的時間過程成分x(k)∈rl×t，k＝1,…,k；帶通濾波器截止頻率fl～fh可根據tc成分的頻率特性進行選擇，對於靜息態fmri數據，可選為0.015～0.15(單位hz)；

第三步，對於sbn分析方法，逐個被試計算：令k＝1；

第四步，設置停機參數ε，約束參數λ1，λ2，利用圖2所示的sbn方法實現流程，由濾波數據x(k)∈rl×t計算第k個被試共l個節點的sbn回歸係數矩陣i,j＝1,…,l，i≠j；

第五步，判斷k是否小於k，若是，則k＝k+1，並跳轉到第四步；若否，則跳轉到第六步；

第六步，剔除非顯著連接，保留顯著連接：對於k個被試的各個相同連接的i,j＝1,…,l，i≠j，例如分別利用單樣本t檢驗計算t值，保留ptth的顯著性連接，剔除其他連接；tth是在自由度為k-1的情況下，p<0.05所對應的t值，可查表得到。例如，k＝82時，tth＝1.99；

第七步，對於顯著連接，計算k個被試的各回歸係數的平均值，記為

第八步，約束回歸係數：挑選出回歸係數的連接，剔除的連接；β′可根據對的約束強度進行設置，約束強度越大，β′越大；

第九步，對於granger因果連接分析方法，逐個被試計算：令k＝1；

第十步，計算第k個被試數據x′(k)中每兩個tc成分間的因果一致性和i,j＝1,…,l，i≠j。根據公式(1)(2)(3)(4)，若tc成分i與成分j的時間序列用xt與yt表示，那麼：

式中，

第十一步，判斷k是否小於k，若是，則k＝k+1，並跳轉到第十步；若否，則跳轉到第十二步；

第十二步，剔除非顯著連接，保留顯著連接：對於k個被試的各個相同連接的因果一致性參數和i,j＝1,…,l，i≠j，例如分別利用單樣本t檢驗計算t值，保留ptth的顯著性連接，剔除其他連接；tth的意義同第六步介紹；

第十三步，對於顯著連接，計算k個被試的各因果一致性的平均值，記為和

第十四步，約束因果一致性差值：挑選出的連接，剔除的連接；c′可根據對的約束強度進行設置，約束強度越大，c′越大；

第十五步，對於上述sbn分析與granger因果分析得到的連接結果，參見第八步和第十四步結果，檢測兩種方法的相同連接；

第十六步，輸出兩種方法的相同連接，作為穩定連接。

本發明所達到的效果和益處是，通過利用雙約束聯合分析方法，建立sbn與granger兩種有效連接分析方法之間的橋梁，提取穩定而魯棒的腦功能連接，為基於fmri數據的腦功能研究和腦疾病診斷提供更好的技術支持。例如，以默認網絡(defaultmodenetwork,dmn)內部7個子成分為對象(見圖4-圖8)，以本發明提取的穩定連接(見圖8)為目標網絡，採用granger有效連接分析方法對40個健康被試對照組與42個精神分裂症患者組進行有效連接分析，結果表明，精神分裂症患者組與健康對照組在目標網絡的連接結果上存在顯著差異，可用於精神分裂症分類。

附圖說明

圖1是五節點bn有向無環圖示例；

圖2是sbn方法的實現流程圖；

圖3是本發明的流程圖；

圖4是對82個被試靜息態fmri數據7個dmn子網絡進行sbn分析所得的顯著連接結果圖；

圖5是對sbn的顯著連接結果施加回歸係數約束後得到的功能連接圖；

圖6是對82個被試靜息態fmri數據7個dmn子網絡進行granger分析所得的顯著連接結果圖；

圖7是對granger的顯著連接分析結果施加因果一致性差值約束後得到的有效連接圖；

圖8是sbn和granger聯合分析輸出的穩定連接。

具體實施方式

下面結合技術方案和附圖，詳細敘述本發明的一個具體實施例。

現有82個被試(k＝82)的靜息態fmri數據，利用gift工具箱(http://mialab.mrn.org/software/gift/index.html)提供的groupica方法(v.calhoun,t.adali,g.pearlson,andj.pekar,amethodformakinggroupinferencesfromfunctionalmridatausingindependentcomponentanalysis,humanbrainmapping14:140-151,2001)，採用infomax算法分離得到120個腦空間激活區成分及其對應的tc成分。根據smith腦空間激活區參考模板(s.m.smith,p.t.fox,k.l.miller,d.c.glahn,p.m.fox,c.e.mackay,etal.,correspondenceofthebrain’sfunctionalarchitectureduringactivationandrest,proceedingsofthenationalacademyofsciences106(31):13040-13045,2009)，按照相關最大化原則挑選出默認網絡(defaultmodenetwork,dmn)的l＝7個感興趣子網絡，提取其對應於每個被試的7個tc成分，每個tc成分的時間點數t＝150，沒有先驗結構信息。實施本發明的步驟如圖3所示，具體如下：

第一步，輸入從82個被試fmri數據中分別提取的7個tc成分，記為x′(k)∈r7×150,k＝1,…,82；

第二步，採用截止頻率為0.015～0.15(單位hz)的帶通濾波器對x′(k)進行濾波，得到濾波後的時間過程成分x(k)∈r7×150，k＝1,…,82；

第三步，對於sbn分析方法，逐個被試計算：令k＝1；

第四步，設置停機參數ε＝0.01，約束參數λ1＝50，λ2＝10[(t-1)2l/λ1-λ1]＝30581.4，利用圖2所示的sbn方法實現流程，由濾波數據x(k)∈r7×150計算第k個被試共7個節點的sbn回歸係數矩陣i,j＝1,…,7，i≠j；

第五步，判斷k是否小於82，若是，則k＝k+1，並跳轉到第四步；若否，則跳轉到第六步；

第六步，剔除非顯著連接，保留顯著連接：對於82個被試的各個相同連接的i,j＝1,…,7，i≠j，分別利用單樣本t檢驗計算t值，保留p1.99的顯著性連接，剔除其他連接，結果如圖4所示；

第七步，對於顯著連接，計算82個被試的各回歸係數的平均值，記為

第八步，約束回歸係數：挑選出回歸係數的連接，剔除的連接，結果如圖5所示；

第九步，對於granger因果連接分析方法，逐個被試計算：令k＝1；

第十步，利用公式(8)(9)，計算第k個被試數據x′(k)中每兩個tc成分間的因果一致性和i,j＝1,…,7，i≠j；

第十一步，判斷k是否小於82，若是，則k＝k+1，並跳轉到第十步；若否，則跳轉到第十二步；

第十二步，剔除非顯著連接，保留顯著連接：對於82個被試的各個相同連接的因果一致性參數和i,j＝1,…,7，i≠j，分別利用單樣本t檢驗計算t值，保留p1.99的顯著性連接，剔除其他連接，結果如圖6所示；

第十三步，對於顯著連接，計算82個被試的各因果一致性的平均值，記為和

第十四步，約束因果一致性差值：挑選出的連接，剔除的連接，結果如圖7所示；

第十五步，對於上述sbn分析與granger因果分析得到的連接結果，參見圖5和圖7的結果，檢測兩種方法的相同連接；

第十六步，輸出兩種方法的相同連接，見圖8，作為穩定連接。