一種基於組合優化的近紅外無創血糖檢測波長變量篩選方法與流程
2023-08-03 04:14:11 1
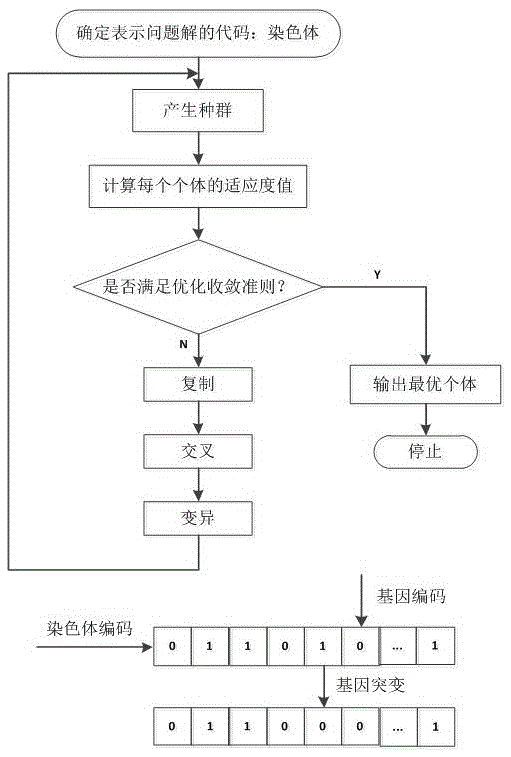
本發明屬於近紅外光透射法無創血糖檢測技術領域,具體涉及了一種組合優化算法用於人體無創血糖檢測的近紅外光波長變量選擇方法。
背景技術:
近年來,隨著化學計量學的發展和光學元件設計製造水平的提升,使得近紅外(NIR,Near infrared)光譜分析技術用於人體血糖的無創檢測的理念和實踐越來越成熟。通過LED近紅外光源透射法建立與人體血糖濃度間的回歸模型,可以用於對人體血糖濃度進行預測。工程應用中可供選擇的不同波長的LED較多。在NIR結合PLS方法建模中,若採用不同波長的LED光源個數過多,模型計算量很大,且在某些光譜區域,血糖的光譜信息很弱,有的和其它成分吸收譜峰重疊嚴重,建立的模型很容易產生過擬合現象。所以,通過特定方法篩選特徵波長或波長區間有可能得到更好的定量校正模型。波長選擇一方面可以簡化模型,另一方面由於不相關或非線性變量的剔除,可以得到預測能力強、穩健性好的校正模型。
在工程實際應用中,如何從眾多近紅外LED光源波長變量中篩選出合適的光源,迄今為止還沒有一個公認的篩選方法,特別是在人體無創血糖檢測近紅外光譜中波長選擇更是鮮有報導。目前發展出的一些計算方法,主要分為基於閾值的簡單判斷方法和基於搜索方式確定最佳波長組合的方法。閾值方法主要是以相關係數等作為指標,其適用性不是很高;基於搜索方法一般以選擇的波長建立PLS或PCR等線性回歸模型的均方根誤差(RMSE)作為優化目標函數,常用的搜索方法有逐步選擇算法、模擬退火算法、多鏈方法和遺傳算法等,但在實際人體無創血糖測量過程中,由於檢測條件和檢測方式變化多樣,這些搜索方法都存在一定的局限性,很難達到全局最優結果。遺傳算法雖然應用非常廣泛,但由於NIR的初始群體是隨機選取的,叉變異過程也有較強的隨機性,每次波長選擇的結果不能保證一致,且根據經驗,校正集中波長變量與樣本數的比值一般要小於4,否則得到的結果是不可靠的;總之通過單一搜索方法選擇的波長變量建立的模型其魯棒性並不是很高,模型需要頻繁的校正。
技術實現要素:
為了解決上述單一搜索方法選擇變量上會陷入局部最優、模型魯棒性不強的技術問題,本發明提供了一種基於加權組合優化方式選擇波長變量的方法,該方法以逐步選擇算法、連續投影算法和遺傳算法為基礎,從中篩選出更為合理,魯棒性更高的波長變量,本發明包括如下步驟:
步驟1、通過臨床試驗得到的不同時間段不同濃度的人體血糖值,同時用多個不同波長的LED光源通過非侵入方式獲得人體血糖近紅外透射率光譜數據;
步驟2、然後建立偏最小二乘回歸模型,以誤差均方根(RMSE)為指標,分別採用連續投影算法、遺傳算法和逐步選擇算法篩選出各自最優波長變量組,作為初始變量組;
步驟3、再對三組變量進行得分評價,將模型複測定係數歸一化作為每組間的權值,組內的得分由每個輔助變量對模型的貢獻程度t檢驗來得到,t越大,則該變量得分越高,考慮到組間各變量得分的平衡性,對每組內變量的t檢驗得分也進行歸一化處理;
步驟4、對變量得分進行加權,將步驟3得到的組間權值和組內得分進行相乘,若組間變量相同則進行評分累加,最後得到的評分按高低排序;
步驟5、選擇評分最高的前k個波長變量作為最終輔助變量。
與現有技術相比,本發明具有以下優點:
在近紅外LED光透射法用於無創血糖檢測中,將過多的波長變量篩選為數量更少的獨立變量,不僅降低了模型複雜度和大大提高了計算效率,而且去除了大多冗餘信息,能夠提高模型預測能力;該方法綜合連續投影算法、遺傳算法和逐步選擇算法三種變量選擇算法,以各變量對模型貢獻度作為得分指標,模型複測定係數作為權重,加權優化得出最優變量組,能有效克服單一算法的局限性,減少了預測模型需要頻繁校正的現象,魯棒性更強;本發明涉及算法穩定、效率高,適用於大規模的變量選擇優化問題。
附圖說明
圖1為本發明提供的基於組合優化的近紅外無創血糖檢測波長變量篩選方法的流程示意圖。
圖2為本發明提供的遺傳優化算法示意圖。
具體實施方式
以下結合變量篩選流程圖對本發明作進一步的詳細說明,但本發明的保護範圍並不局限於此。
本發明方法的整體流程如圖1所示,基於組合優化的近紅外無創血糖檢測波長變量篩選方法具體的實施步驟如下:
步驟一(圖1)、數據的獲取,通過臨床試驗獲得不同時間段人體血糖濃度值的數據,同時使用多個不同波長的近紅外LED光源對手臂或耳垂部位進行掃描,為了測量準確,需要進行多次掃描取平均值,並對數據進行平滑預處理。
步驟二(圖1、圖2)、建立線性回歸(如PLSR、PCR等)校正模型;
PLSR的基本做法是首先在自變量集中提出第一成分t1(t1是x1、x2、…xm的線性組合,且儘可能多地提取原自變量中的變異信息);同時在因變量集中也提取第一成分u1,並要求t1與u1相關程度達到最大;然後建立因變量y1、y2、…yp與t1的回歸,如果回歸方程已達到滿意的精度,則算法中止;否則繼續對第二成分的提取,直到達到滿意的精度為止;若最終對自變量集提取個成分t1、t2、…tr,PLSR將通過建立y1、y2、…yp與t1、t2、…tr的回歸式,然後再表示為y1、y2、…yp與原自變量的回歸方程式,模型誤差均方根表示如下:
以RMSE作為評價模型預測效果的優劣的指標。
步驟三(圖1)、根據步驟二,分別用連續投影算法、遺傳算法和逐步回歸法對原始光譜數據進行處理,以PLS模型誤差均方根為指標,選擇各自有效的波長變量組。連續投影算法步驟如下:
(1)初始化:n=1(第一次迭代),在光譜矩陣中任選一列向量xj,記為xk(0)(k(0)=j);
(2) 集合S定義為:,即還沒有被選擇進波長鏈的列向量,分別計算xj對S中向量的投影向量
(3)記錄最大投影的序號
(4)將最大的投影作為下輪的投影向量
這樣得到對波長組合,對每一對xk(0)和N所決定的組合分別建立定標模型,使用預測RMSE來判斷所建模型的優劣,選出最小的RMSE,它所對應的xk(0)*和N*即為最佳的波長組合;
遺傳算法是仿照生物進化和遺傳的規律,根據「生存競爭」和「優勝劣汰」的原則,從任一初始群體出發,通過複製、交換、突變等操作,使優勝者繁殖,劣汰者消失,一代一代重複同樣的操作,最終使解決問題逼近最優解,將其用于波長變量篩選也是一個比較有效的方法。對群體進行編碼,編碼方式採用二進位0/1字符編碼,對變量數為m的問題,可用一個有m字符的字符串來表示每種變量組合,字符串中的每個字符用0或1表示,0代表對應的變量未被選中,1代表對應的變量選中,算法流程圖如圖2所示;
逐步選擇方法的原理是:每一步只引入或剔除一個自變量,自變量是否被引入或剔除則取決於其偏回歸平方和的F檢驗或校正決定係數。如方程中已引入了(m-1)個自變量,在此基礎上考慮再引入變量Xj。記引入Xj後方程(即含m個自變量)的回歸平方和為SS回歸,殘差為SS殘差;之前含(m-1)個自變量(不包含Xj )方程的回歸平方和為SS回歸(-j) ,則Xj的偏回歸平方和為 U = SS回歸-SS回歸(-j),檢驗統計量為:
如果Fj>Fa(1 ,n - m - 1)(a為置信度),則 Xj選入方程;否則,不入選。從方程中剔除無統計學作用的自變量,過程則相反,但檢驗一樣。
步驟四(圖1)、 經過連續投影算法、遺傳算法和逐步回歸算法與PLS回歸建模結合,分別篩選得到N、M和P個變量的組合,再分別以該三組變量組進行回歸建模,並計算模型複測定係數,和三組變量中每個變量的貢獻度,複測定係數計算公式如下:
三個模型得到的複測定係數分別為R12、R22和R32,複測定係數越大,說明模型回歸效果越好,為了計算得分平衡性,按如下公式對其進行歸一化,將歸一化後的w作為每組間的得分權值:
組內得分則通過每個變量對模型的貢獻即顯著性t檢驗來求得:
其中,bj是第j個變量的回歸係數,n樣本數,m變量數;, cii是c的對角線上第i個的元素,;然後對tj進行歸一化處理作為變量組內的得分。
步驟五(圖1)、對三組變量進行加權打分,將三組變量中相同變量得分進行加權累積,公式如下:
其中,wi 是變量組間權值,tij是第j個變量在第i組內的得分,對Tj進行高低排序,再按照一定原則選取前k個變量作為最終模型變量。
以上所述僅是本發明的優選實施方式,應當指出,對於本技術領域的普通技術任一來說,再不脫離本發明原理的前提下,還可以做出若干改進和潤飾,這些改進和潤飾也應視本發明的保護範圍。
