基於顯式差分格式的電磁特性提取方法與流程

2023-06-01 22:57:31

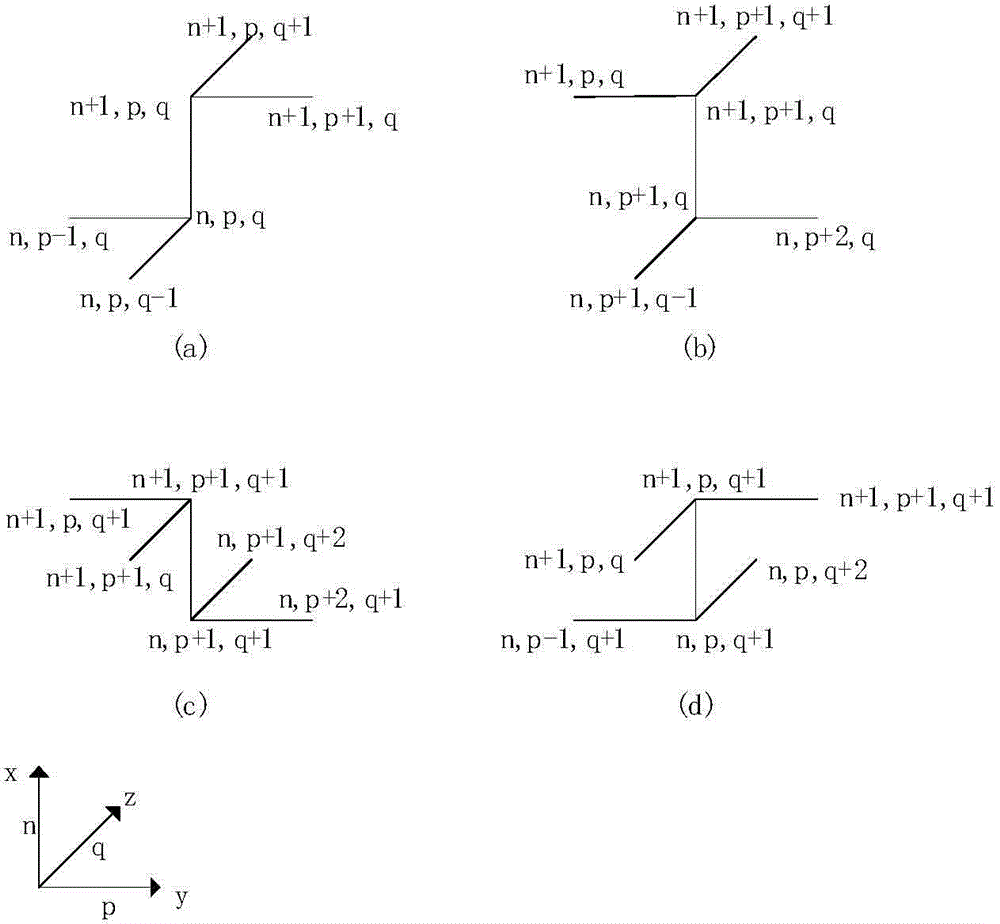
本發明屬於目標電磁散射特性
技術領域：
，特別是一種基於顯式差分格式的電磁特性提取方法。
背景技術：
：電磁計算的數值方法如矩量法(MOM)、有限元法(FEM)、時域有限差分方法(FDTD)可以很好地解決電小尺寸物體的散射，但在計算電大物體的散射時，對計算機的配置要求過高。近似方法如射線跟蹤、物理光學等高頻方法則只能求解規則形狀的電大物體的散射。迭代推進方法是用於求解目標散射問題的一種比較新型的方法，世界上許多國家主要在空間場的迭代遞推、電流的迭代遞推和時域場的迭代遞推等方面做了大量的研究並取得一定的研究成果。拋物線方程方法屬於迭代推進方法，它是波動方程的一種近似形式，假設電磁波能量在沿著拋物線軸向的錐形區域內傳播。拋物線方程方法為求解電磁散射提供了一種準確、高效的計算方法，它的主要缺陷是只能對拋物線方向近軸區域內的電磁散射進行快速、準確地計算，不過這種限制可以通過旋轉拋物線軸向來克服，主要思想是拋物線的軸向不受入射場方向的限制，使拋物線的軸向圍繞散射目標旋轉來計算目標任意方向的散射場。A.A.Zaporozhets和M.F.Levy在文章「BistaticRCSCalculationswiththeVectorParabolicEquationMethod」中首次將拋物線方程方法來分析電磁散射問題，用拋物線方程方法計算目標的電磁散射問題，特別用於計算電大尺寸目標的散射時發現拋物線方程方法與以往的電磁計算方法相比具有快速、準確的特點。隨著拋物線方程方法的不斷發展，R.Martelly和R.Janaswamy在文章「ModelingRadioTransmissionLossinCurved,BranchedandRough-WalledTunnelswiththeADI-PEMethod」中提出了採用交替方向隱格式的差分方法來分析隧道中波的傳播問題，從而降低了計算的內存需求以及時間需求，但是現有技術中沒有將該方法應用於電磁散射問題。技術實現要素：本發明的目的在於提供一種基於顯式差分格式的電磁特性提取方法，該方法將每個切面分為三部分分別進行求解，能夠快速得到電磁散射特性參數。實現本發明目的的技術解決方案為：一種基於顯式差分格式的電磁特性提取方法，步驟如下：步驟1、建立散射體的離散模型，確定拋物線的軸向方向作為x軸，採用網格對散射體沿拋物線的軸向方向進行離散處理，形成垂直於x軸的若干個切面，在每個切面上將散射體的邊界點以及內部點標示出來；步驟2、將每個切面劃分成三個區域，距離散射體由近至遠依次為第一區域、第二區域和第三區域，第一區域和第二區域均為空氣層，第三區域為完全匹配層；對第二和第三區域採用交替組顯迭代方法顯示求解散射場場值，對第一區域採用交替方向隱格式求解散射場場值；步驟3、令x軸方向為待求的散射方向，依次對沿軸向方向的各個切面上的離散節點散射場場值按步驟2的方法進行遞推求解，求解最後一個切面的散射場場值後，根據遠近場轉換求解目標散射體雙站雷達散射截面積。本發明與現有技術相比，其顯著優點為：(1)空氣層及PML區域使用顯格式差分求解散射場場值，計算速度能夠顯著加快；(2)散射體附近區域使用交替方向隱格式求解，形成的矩陣為三對角矩陣，可通過追趕法求解，計算速度顯著提高；(3)各個區域每個切面的散射場場值計算互相獨立，可通過並行提高計算效率。下面結合附圖對本發明作進一步詳細描述。附圖說明圖1是本發明劃分的三個區域示意圖。圖2是本發明交替組顯迭代方法的差分格式示意圖。圖3是本發明交替方向隱格式方法的計算步驟示意圖。圖4是本發明實施例的散射體示意圖。圖5是本發明實施例中散射體雙站RCS曲線圖。具體實施方式下面結合附圖對本發明作進一步詳細描述。結合附圖1～2，本發明將交替分組顯示格式和交替方向隱格式方法引入到拋物線方程方法中，電磁特性提取方法步驟如下：步驟1、建立散射體的離散模型，確定拋物線的軸向方向作為x軸，採用網格對散射體沿拋物線的軸向方向進行離散處理，形成垂直於x軸的若干個切面，在每個切面上將散射體的邊界點以及內部點標示出來；步驟1.1、對散射體進行三角面元的面剖分，確定軸方向每個切面的方程，通過剖 分網格的幾何關係求解三角面元與切面的交點，與該交點距離最近的差分網格點標記為邊界點並求出該點法向分量；步驟1.2、對散射體進行四面體的體剖分，通過判斷某點是否處於四面體內部來區分該點處於散射體內部或者散射體外部，並對這些點進行標記。步驟2、將每個切面分成三個區域進行求解，如圖1所示，距離散射體由近至遠依次為第一區域、第二區域和第三區域，第一區域和第二區域均為空氣層，第三區域為PML層；對第二和第三區域採用交替組顯迭代方法顯示求解，對第一區域採用交替方向隱格式求解，具體包括以下步驟：步驟2-1、如圖1所示，首先計算第二區域空氣層的散射場場值，拋物線方程的交替組顯迭代方法(AGE)是指利用交替組顯迭代左單點(GEL)和交替組顯迭代右單點(GER)兩種方法在x方向交替迭代求解；設第二區域的離散點個數為M*M，M為自然數，將拋物線方程按圖2所示的非對稱格式差分展開，建立組顯示格式，並將方程聯立寫成矩陣形式可得：up,qn+1up+1,qn+1up+1,q+1n+1up,q+1n+1=A-1r1up-1,qn+(1-r1-r2r)up,qn+r2up,q-1nr1up+2,qn+(1-r1-r2)up+1,qn+r2up+1,q-1nr1up+2,q+1n+(1-r1-r2)up+1,q+1n+r2up+1,q+2nr1up-1,q+1n+(1-r1-r2)up,q+1n+r2up,q+2n---(6)]]>其中A-1=1(1+2r1)(1+2r2)(1+2r1+2r2)MNLSNMSLLSMNSLNM---(7)]]>M=1+3r1+3r2+6r1r2+2r12+2r22+2r12r2+2r1r22]]>N=r1+2r1r2+2r12+2r12r2+2r1r22S=r2+2r1r2+2r22+2r12r2+2r1r22---(8)]]>L＝2r1r2(1+r1+r2)其中i為虛部，k為自由空間波數，△x,△y,△z分別為x,y,z方向上的離散間隔的大小，代表在(n,p,q)處的散射場場值，n,p,q分別代表在x,y,z 方向上的離散網格的個數，1≤p≤M，1≤q≤M，1≤n≤N，N為切面的總個數；首先，給出GEL方法的表達式；第二區域左下角靠近邊界的內點的散射場場值為：u1,1n+1=11+r1+r2[r1u2,1n+(1-r1-r2)u1,1n+r2u1,2n]---(9)]]>第二區域左邊靠近邊界的一列的散射場場值為：u1,qn+1u1,q+1n+1=1r12+2r1r2+2r1+2r2+11+r1+r2r2r21+r1+r2r1u2,qn+(1-r1-r2)u1,qn+r2u1,q-1nr1u2,q+1n+(1-r1-r2)u1,q+1n+r2u1,q+2n---(10)]]>上式中，q＝2,4,...,M-2；第二區域下邊靠近邊界的一行的散射場場值為：up,1n+1up+1,1n+1=1r22+2r1r2+2r1+2r2+11+r1+r2r1r11+r1+r2r1up-1,1n+(1-r1-r2)up,1n+r2up,2nr1up+2,1n+(1-r1-r2)up+1,1n+r2up+1,2n---(11)]]>上式中，p＝2,4,...,M-2；同理，給出GER方法的表達式；第二區域右上角靠近邊界的內點的散射場場值為：uM-1,M-1n+1=11+r1+r2r1uM-2,Mn+r2uM-1,M-2n+(1-r1-r2)uM-1,M-1n---(12)]]>第二區域右邊靠近邊界的一列的散射場場值為：uM-1,qn+1uM-1,q+1n+1=1r12+2r1r2+2r1+2r2+11+r1+rr2r21+r1+rr1uM-2,qn+(1-r1-r2)uM-1,qn+r2uM-1,q-1nr1uM-2,q+1n+(1-r1-r2)uM-1,q+1n+r2uM-1,q+2n---(13)]]>上式中，q＝1,3,...,M-3第二區域上邊靠近邊界的一行的散射場場值為：up,M-1n+1up+1,M-1n+1=1r22+2r1r2+2r1+2r2+11+r1+r2r1r11+r1+r2r1up-1,M-1n+(1-r1-r2)up,M-1n+r2up,M-2,nr1up+2,Mn+(1-r1-r2)up+1,Mn+r2up+1,M-2n---(14)]]>上式中，p＝1,3,...,M-3對於第二區域其它離散點的散射場場值用式(6)計算；類似於自由空間的求解，第三區域PML媒質中的拋物線方程表示為：ux=i2k[(11-iσ(y))22uy2+2iσ0y(1-iσ(y))3δ2uy+(11-iσ(z))22uz2+2iσ0z(1-iσ(z))3δ2uz]---(15)]]>按照如圖2所示的非對稱格式展開，並寫成矩陣形式：up,qn+1up+1,qn+1up+1,q+1n+1up,q+1n+1=-FZF0-1c+d-1c+d0+RFZ-RFup,qn(1-a-c)+aup-1,qn+cup,q-1nup+1,qn(1-a-c)+aup+2,qn+cup+1,q-1nup+1,q+1n(1-a-c)+aup+2,q+1n+cup+1,q+2nup,q+1n(1-a-c)+aup-1,q+1n+cup,q+2n---(16)]]>其中：Z=a-bc+d-1+a+c-b-dc+d-1+a+c+b-dc+da+bc+d---(17)]]>R=a-bc+d-1+a+c-b+dc+d-1+a+c+b+dc+da+bc+d---(18)]]>F=c+d(a2-c2)2+(1+a+c)2[(1+a+c)2-2c2-2a2](a2-c2)2+(1+a+c)2[(1+a+c)2-2c2-2a2]+[b2+c2-a2-(1+a+c-b)2][b2+c2-a2-(1+a+c+b)2]2(1+a+c)(b-a)b2+c2-a2-(1+a+b+c)2b2+c2-a2-(1+a-b+c)22(1+a+c)(b-a)---(19)]]>a=1(1-iσ0(y/δ)2)2ΔxΔy2]]>b=2iσ0y(1-iσ0(y/δ)2)3δ2ΔxΔy---(20)]]>c=1(1-iσ0(z/δ)2)2ΔxΔz2]]>d=2iσ0z(1-iσ0(z/δ)2)3δ2ΔxΔz]]>其中，σ(y)＝σ0(y/δ)2，σ(z)＝σ0(z/δ)2,η＝120π，R0＝10-3，δ為PML媒質的厚度；步驟2-2、第三區域PML媒質中的GEL格式表達式表示為：第三區域左下角靠近邊界的內點的散射場場值為：u1,1n+1=u1,1n(1-a-c)+au2,1n+cu1,2n1+a+c-b-d---(21)]]>第三區域左邊靠近邊界的一列的散射場場值為：u1,qn+1u1,q+1n+1=B1B2B3B4u1,qn(1-a-c)+au2,qn+cu1,q-1nu1,q+1n(1-a-c)+au2,q+1n+cu1,q+2n---(22)]]>q＝2,4,...,M-2其中，B1=1+a+c-b-d(1+2c+a-b)(1+a-b)]]>B2=c+d(1+2c+a-b)(1+a-b)B3=(1+c+d+a-b)(1+c+a-b-d)(1+2c+a-b)(1+a-b)(c+d)-1c+d---(23)]]>B4=1+a+d+c-b(1+2c+a-b)(1+a-b)]]>第三區域下邊靠近邊界的一行的散射場場值為：up,1n+1up+1,1n+1=A1A2A3A4up,1n(1-a-c)+aup-1,1n+cup,2nup+1,1n(1-a-c)+aup+2,1n+cup+1,2n---(24)]]>p＝2,4,...,M-2其中，A1=1+a+c-b-d(1+2a+c-d)(1+c-d)]]>A2=a+b(1+2a+c-d)(1+c-d)A3=(1+a+c+b-d)(1+a+c-b-d)(1+2a+c-d)(1+c-d)(a+b)-1a+b---(25)]]>A4=1+a+c-b-d(1+2a+c-d)(1+c-d)]]>PML媒質中的GER格式表達式為：第三區域右上角靠近邊界的內點的散射場場值為：uM-1,M-1n+1=uM-1,M-1n(1-a-c)+auM-2,M-1n+cuM-1,M-2n1+a+c+b+d---(26)]]>第三區域右邊靠近邊界的一列的散射場場值為：uM-1,qn+1uM-1,q+1n+1=D1D2D3D4uM-1,qn(1-a-c)+auM-2,qn+cuM-1,q-1nuM-1,q+1n(1-a-c)+auM-2,q+1n+cuM-1,q+2n---(27)]]>q＝1,3,...,M-3其中，D1=1+a+c+b-d(1+2c+a+b)(1+a+b)]]>D2=c+d(1+2c+a+b)(1+a+b)D3=(1+c+d+a+b)(1+c+a+b-d)(1+2c+a+b)(1+a+b)(c+d)-1c+d---(28)]]>D4=1+a+d+c+b(1+2c+a+b)(1+a+b)]]>第三區域上邊靠近邊界的一行的散射場場值為：up,M-1n+1up+1,M-1,n+1=C1C2C3C4up,M-1n(1-a-c)+aup-1,M-1n+cup,M-2nup+1,M-1n(1-a-c)+aup+2,M-1n+cup+1,M-2n---(29)]]>p＝1,3,...,M-3其中，C1=1+a+c-b+d(1+2a+c+d)(1+c+d)]]>C2=a+b(1+2a+c+d)(1+c+d)C3=(1+a+c+b+d)(1+a+c-b+d)(1+2a+c+d)(1+c+d)(a+b)-1a+b---(30)]]>C4=1+a+c+b+d(1+2a+c+d)(1+c+d)]]>對於第三區域其它離散點採用式(16)計算；步驟2-3、對第一區域散射體的離散節點，採用如圖3所示的拋物線方程交替方向隱格式方法求解：-iry4k1+iry2k-iry4kup-1,qn+1/2up,qn+1/2up+1,qn+1/2=irz4k1-irz2kirz4kup,q-1nup,qnup,q+1n---(31)]]>-irz4k1+irz2k-irz4kup,q-1n+1up,qn+1up,q+1n+1=iry4k1-iry2kiry4kup-1,qn+1/2up,qn+1/2up+1,qn+1/2---(32)]]>可以看出式(31)可由前一個切面的散射場場值按行求出中間虛擬面上的未知值，式(32)可由中間虛擬面上的值按列求出下一個切面上的散射場場值；其中，ry＝2△x/△y2，rz＝2△x/△z2，△x、△y、△z分別為x、y、z方向上差分網格點的長度。步驟3、令x軸方向為待求的散射方向，依次對沿軸向方向的各個切面上的離散節點散射場場值按步驟2介紹的方法進行遞推求解，求解出最後一個切面散射場場值後，根據近遠場轉換求解目標散射體雙站RCS；具體步驟如下：首先根據步驟2介紹的方法計算出迭代求解時最後一個面的散射場場值；其次根據近遠場轉換得到遠場的散射場場值；最後在三維坐標系下，在(θ,φ)方向的雙站RCS為：σ(θ,φ)=limr∞4πr2|Es(x,y,z)|2|Ei(x,y,z)|2---(23)]]>其中Es和Ei分別表示散射場和入射場的電場分量，π為圓周率， θ代表球坐標系下向量(x,y,z)與z軸的夾角，φ代表球坐標系下向量(x,y,z)與xoy面的夾角。下面結合具體實施例對本發明作進一步說明。實施例本實施例對目標電磁散射特性進行了提取仿真，仿真在主頻2.86GHz、內存8GB的個人計算機上實現，提取對象為一架戰鬥機F15，如圖4所示，入射波頻率為5GHz，入射波的方向為了驗證本發明方法的正確性，以快速多級子(MLFMM)仿真結果作為參照；圖5為電磁散射特性仿真的RCS曲線圖，從圖中的曲線可以看出，本文方法與正確的數值結果吻合，另外表1為本發明與快速多級子方法(MLFMM)、基於CN差分的拋物線方程方法(CN-PE)以及基於ADI的拋物線方程方法(ADI-PE)進行時間及內存上的對比結果：表1本發明與其它方法時間及內存上的比較表1表明本發明的方法與其他現有方法相比，能夠更有效地快速提取電大尺寸目標物體的電磁散射特性。本發明結合交替組顯迭代方法和交替方向隱格式方法對計算區域進行求解，加速了每個切面的求解速度。本發明在計算電大金屬目標的電磁散射特性分析中能夠節省計算時間，並且有利於並行求解，具有很強的實際工程應用價值。當前第1頁1&nbsp2&nbsp3&nbsp