一種基於矩陣的低秩稀疏人臉識別方法及其系統與流程
2023-05-26 00:25:31 6
本發明屬於模式識別技術改進領域,尤其涉及一種基於矩陣的低秩稀疏人臉識別方法及其系統。
背景技術:
智慧城市理念的提出意味著城市要啟動智能化的進程,其中一個方面是通過視頻監控、智能識別減少城市犯罪率。而這一個想法的實現最為重要的環節是提升人臉識別的成功率。而在人臉識別技術領域中,如何從高維度的圖像中提取出有用的特徵並減少數據維度,具有非常重要的研究意義。因為高維度的圖像不僅加大了計算複雜度,還存在大量冗餘的信息嚴重影響分類器的識別成功率,所以如何有效的對圖像進行特徵提取則顯得尤為重要了。在這樣的需求下,大量的特徵提取算法被相繼提出。其中較為經典的有基於圖像全局結構的主成分分析技術pca和線性鑑別分析技術lda。基於圖像局部結構的局部線性嵌入技術lle和正交鄰域保留投影技術onpp。這幾個經典的特徵提取技術由於其大大提高了圖像識別率,被廣泛運用在了人臉識別,指紋識別等應用上。然而,隨著技術的發展,人們發現了經這些經典的特徵提取技術所產生的投影矩陣不夠稀疏,所以對於特徵提取的結果缺乏可靠的解釋性,這在一定程度上影響了算法的有效性。
因此在這些技術的基礎上,人們還提出了許多基於稀疏表示的特徵提取技術。比如基於pca提出的spca,基於lda提出的sda,基於onpp提出的sle等等。稀疏表示的主要目的是進一步突出圖像的主要特徵,讓大多數冗餘信息變為零。經過改進後的稀疏特徵提取技術通過對投影矩陣增加約束範數,讓模型選擇更具有鑑別力的投影元素,從而從根本上改變了投影矩陣的組成成分,讓提取結果更負說服力。稀疏表示的另一個好處就是投影矩陣的大部分元素變成零,程序運算速度因此大大增加。
以上方法均是基於圖像向量的特徵提取技術,與之對應的,便是基於圖像矩陣的方法。基於圖像矩陣的特徵提取技術能更好的挖掘圖像的結構化信息同時增加算法的計算效率。傳統的特徵提取技術習慣於將圖像矩陣轉化為一維的向量後再進行處理,這不僅讓圖像從低維度轉變成高維度,還把原本的結構信息忽略了,除此之外,基於一維向量的方法容易產生因訓練樣本太少而導致散列矩陣奇異的問題。基於二維圖像的特徵提取技術自然而然的避免了這些問題,所以一經提出便引起了廣泛的關注,比如從pca技術衍生出的2-dpca,-2-dpca,從lda技術衍生出的2-dlda。
上述基於二維圖像的特徵提取技術在模式識別領域裡被頻繁的利用並展現出良好的性能,但是這些技術仍然存在一些缺陷,若是對此加以改進,識別效果會再進一步提升。
以上介紹的基於二維圖像的特徵提取技術仍然存在一些缺陷,主要是以下兩點:①魯棒性不足。魯棒性不足的原因是由於這些技術普遍採用對噪聲較為敏感的l1或l2範數作為矩陣度量,導致算法在面對噪聲較多或不完整的圖像時變得不穩定且低效。事實上我們所獲得的圖像的清晰度主要依賴於拍攝設備的解析度和拍攝角度,而在監控視頻中獲得一張清晰且完整的圖像是較為困難的,也就是說魯棒性不足的問題亟待解決。而本發明將採用核範數作為主要的約束範數達到低秩學習的效果,從而解決魯棒性不足的問題。②不具備聯合稀疏的功能。雖然spca和sda能夠產生稀疏投影矩陣,但它們都是基於一維向量的特徵提取技術且同樣有魯棒性不足的問題。缺乏聯合稀疏的性質讓算法所提取出的特徵缺乏可靠的解釋性,算法的性能也因此降低,為此我們需要提出一個能夠進行稀疏特徵提取的基於二維圖像的技術。不同於spca等技術採用l2範數作為正則項選擇有鑑別力但隨機性大的特徵,本發明將利用l2,1範數作為正則項進行聯合稀疏學習,進一步提升人臉識別性能。
技術實現要素:
本發明的目的在於提供一種基於矩陣的低秩稀疏人臉識別方法,旨在解決上述的技術問題。
本發明是這樣實現的,一種基於矩陣的低秩稀疏人臉識別方法,所述低秩稀疏人臉識別方法包括以下步驟:
a、對任意人臉樣本進行特徵提取;
b、針對特徵提取後數據進行判別分類並給出人臉識別結果。
本發明的進一步技術方案是:所述步驟a包括以下步驟:
a1、初始化迭代步驟t=1,初始化u(0)為隨機列正交矩陣,p(0)為隨機矩陣,g(0)為單位矩陣;
a2、通過迭代操作,求出稀疏投影子空間p;
a3、將計算得到的進行歸一化處理,其公式為:
a4、計算映射後的人臉特徵矩陣,其公式為:yi=ptxip(i=1,...,n)。
本發明的進一步技術方案是:所述步驟a2中包括以下步驟:
a21、判斷迭代過程中t的大小是否大於tmax;如小於等於tmax,則執行步驟a22,如大於tmax,則執行步驟a3;
a22、利用矩陣x,u(t-1),p(t-1)和函數式計算得出其函數式為:
a23、利用等式關係將矩陣p(t)進行更新,其中等式:
a24、對做svd分解得到
a25、通過函數式對矩陣進行更新並且使得t=t+1,其中函數式:
本發明的進一步技術方案是:所述步驟b中還包括以下步驟:
b1、對提取後的訓練集和測試集的數據使用最近鄰分類器進行判別分類。
本發明的進一步技術方案是:在人臉識別中求得稀疏、有鑑別力的投影矩陣用於把圖像映射到代維空間。
本發明的另一目的在於提供一種基於矩陣的低秩稀疏人臉識別系統,所述低秩稀疏人臉識別系統包括:
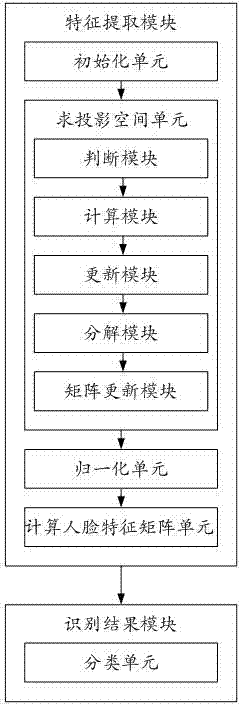
特徵提取模塊,用於對任意人臉樣本進行特徵提取;
識別結果模塊,用於針對特徵提取後數據進行判別分類並給出人臉識別結果。
本發明的進一步技術方案是:所述特徵提取模塊中包括:
初始化單元,用於初始化迭代步驟t=1,初始化u(0)為隨機列正交矩陣,p(0)為隨機矩陣,g(0)為單位矩陣;
求投影空間單元,用於通過迭代操作,求出稀疏投影子空間p;
歸一化單元,用於將計算得到的進行歸一化處理,其公式為:
計算人臉特徵矩陣單元,用於計算映射後的人臉特徵矩陣,其公式為:
yi=ptxip(i=1,...,n)。
本發明的進一步技術方案是:所述求投影空間單元中包括:
判斷模塊,用於判斷迭代過程中t的大小是否大於tmax;如小於等於tmax,則執行計算模塊,如大於tmax,則執行歸一化單元;
計算模塊,用於利用矩陣x,u(t-1),p(t-1)和函數式計算得出其函數式為:
更新模塊,用於利用等式關係將矩陣p(t)進行更新,其中等式:
分解模塊,對做svd分解得到
矩陣更新模塊,用於通過函數式對矩陣進行更新並且使得t=t+1,其中函數式:
本發明的進一步技術方案是:所述識別結果模塊中還包括:
分類單元,用於對提取後的訓練集和測試集的數據使用最近鄰分類器進行判別分類。
本發明的進一步技術方案是:在人臉識別中求得稀疏、有鑑別力的投影矩陣用於把圖像映射到代維空間。
本發明的有益效果是:用線性稀疏的投影矩陣從高維度的圖像中提取出有鑑別力的特徵,從而提高人臉識別的效率;直接對圖像矩陣進行特徵提取,大大加快了算法的計算速度;用最近較為流行的l*範數替代傳統的子空間學習方法中的l1範數或l2範數作為矩陣距離度量,增強算法的魯棒性;通過加入l2,1範數正則項,算法能對迭代求解過程中有鑑別力的投影進行選擇,從而達到聯合稀疏的效果,這不僅使得投影結果具有更高的可解釋性,還可以進一步提升算法的魯棒性;通過使用l*範數和加入聯合稀疏性,該方法提高了人臉識別的性能以及穩定性。
附圖說明
圖1是本發明實施例提供的基於矩陣的低秩稀疏人臉識別方法的流程圖。
圖2是本發明實施例提供的基於矩陣的低秩稀疏人臉識別系統的結構框圖。
圖3是本發明實施例提供的ar人臉資料庫部分樣本示意圖。
具體實施方式
圖1示出了本發明提供的基於矩陣的低秩稀疏人臉識別方法,其詳述如下:
針對任意一個人臉樣本矩陣我們自定義求出最終的投影空間p的迭代步長tmax和映射後的圖像尺寸di(di≤mi),i=1,2。通過以下操作以後,我們映射後的訓練樣本矩陣記為yi=ptxip(i=1,...,n)。
步驟s1,對任意人臉樣本進行特徵提取;在提取人臉的任意樣本特徵中分為如下步驟:第一步,初始化迭代步驟t=1,初始化u(0)為隨機列正交矩陣,p(0)為隨機矩陣,g(0)為單位矩陣。第二步,通過迭代操作,求出稀疏投影子空間p。在求稀疏投影子空間p時包括以下過程,第1步,判斷迭代步驟t的大小是否大於tmax。如果小於等於tmax,執行下面的操作;如果大於tmax,跳出循環,到第三步;第2步,利用矩陣x,u(t-1),p(t-1)和公式
計算出第3步,利用等式更新矩陣p(t);其中等式:第4步,對做svd分解,得到第5步,利用公式更新矩陣g(t),並且t=t+1。第三步,將計算得到的進行歸一化處理,其利用下述函數式:
第四步,計算映射後的人臉特徵矩陣,其公式為:yi=ptxip(i=1,...,n)。
步驟s2,針對特徵提取後數據進行判別分類並給出人臉識別結果。對提取後的訓練集和測試集的數據使用最近鄰分類器進行判別分類。
在人臉識別中求得稀疏、有鑑別力的投影矩陣用於把圖像映射到代維空間。
本發明提出的基於矩陣表示的低秩稀疏人臉識別(lowranksparsefacerecognition,lrsfr)模型通過使用核範數和實現聯合稀疏提升了最近比較流行的基於矩陣表示的特徵提取方法的性能。並且通過交替迭代的方式,我們可以求得稀疏、有鑑別力的投影矩陣用於把圖像映射到低維空間。
假設訓練樣本表示為其中n代表訓練樣本的總個數,設nc和分別代表類標的個數和第i類樣本的個數。參考以往的研究成果,本發明使用的lrsfr模型首先構造投影矩陣原始的圖像信息通過該矩陣投影到低維的特徵矩陣中,得到的結果表示為
yi=utxi(0.1)
首先定義一些變量用於後面的模型介紹:
①樣本的基於核範數的類內線性散度矩陣變量jw:
其中符號||||*代表核範數,p表示用於計算稀疏子空間的投影矩陣,代表第j類訓練樣本對應的均值。
②樣本的基於核範數的類間線性散度矩陣變量jb:
其中代表全部訓練樣本的均值,代表第j類樣本的平均值。
為了利用核範數增強基於圖像矩陣的特徵提取技術的魯棒性,基本的目標函數定為:
s.t.utu=id(3.4)
其中變量μ∈[0,1]用於平衡兩個散度矩陣的值。為了得到的子空間具有稀疏性進而實現更好的分類效果,本發明在公式(3.4)上使用l2,1範數作為正則項。因此,本發明的最終目標函數為:
s.t.utu=id(3.5)
變量γi與μ有相同的作用。為了解決公式(3.5),我們採用交替迭代的方式。首先固定變量u,p。則從(3.2)和(3.3)可以推導出
其中wi,j=((xi-uptxj)(xi-uptxj)t)-1/4
其中
將公式(3.6)和公式(3.7)代入目標函數(3.5),可以得到如下最小值問題
utu=id(3.8)
其中
然後,我們定義對角矩陣g,其對角元素為
其中pi表示矩陣p的第i行。
固定矩陣u求p,則由公式(3.8-3.10)我們有:
對p求導並令其等於0,移項解得
然後固定矩陣p求u。我們可以看到用公式(3.8)求u時,和γ||p||2,1變成常數項,則(3.8)等同於求解一個最大化問題
s.t.utu=id(3.13)
根據spca論文中的理論四,(3.13)的最優解可以通過對做svd分解得到
則
下面詳細介紹該發明技術方案中所涉及的各個細節問題的說明:
針對任意一個人臉樣本矩陣我們自定義求出最終的投影空間p的迭代步長tmax和映射後的圖像尺寸di(di≤mi),i=1,2。通過以下操作以後,我們映射後的訓練樣本矩陣記為yi=ptxip(i=1,...,n)。
步驟一、特徵提取
(1)初始化。
我們首先初始化迭代步驟t=1,初始化u(0)為隨機列正交矩陣,p(0)為隨機矩陣,g(0)為單位矩陣。
(2)通過迭代操作,求出稀疏投影子空間p。
第一步,判斷迭代步驟t的大小是否大於tmax。如果小於等於tmax,執行下面的操作;如果大於tmax,跳出循環,到(3);
第二步,利用矩陣x,u(t-1),p(t-1)和公式(3.6),(3.7),(3.9)計算出
第三步,利用等式更新矩陣p(t)。
第四步,對做svd分解,得到
第五步,利用公式(3.10)更新矩陣g(t),並且t=t+1。
(3)歸一化。
將計算得到的進行歸一化。
(4)計算映射後的人臉特徵矩陣
yi=ptxip(i=1,...,n)
步驟二、分類
針對特徵提取後的訓練集和測試集數據,我們使用最近鄰分類器進行判別分類,給出人臉識別結果。
下面結合實例對本發明進行詳細的描述。
如圖3所示為本發明所用的ar人臉識別驗證數據樣本圖。本發明所提供的方法在ar上進行了實驗驗證。該庫包括了120個人的人臉圖像,每人有26張不同光照和表性的相片。實驗中我們每個人取10張包括不同光照表情和戴眼鏡的人臉圖片組成一個子集進行實驗,在實驗中,我們隨機選取5張作為訓練數據,剩下的為測試數集。
在實驗中,我們比較了線性鑑別分析方法(lineardiscriminantanalysis,lda)、多線性鑑別分析(multilineardiscrimianantanalysis,mlda)、mlda加lda(mlda+lda)、張量大邊界準則(tensormaximalmarginalcriterion,tmmc)、tmmc加lda(tmmc+lda)、及本專利所提出的lrsfr、lrsfr加lda(lrsfr+lda)人臉識別方法得到的具體實驗結果如下。
表1.識別率的對比
由表1的實驗結果可知,在具有表性、光照和戴眼鏡的情況下,本專利所提供的方法的識別率達到88.46%,比lda高214%;在lrsfr提取特徵並再用lda進行識別時,識別率達到了91.87%。本專利的方法達到大大高於其它方法,包括lda、mlda、mlda+lda、tmmc、tmmc+lda。故本專利所提供的方法較其它方法具有更高的識別性能。其中的主要原因是我們利用了一個更為魯棒的全新的度量方法,該方法所學習得到的投影是不僅是更為魯棒,而且是聯合稀疏的,在特徵提取過程中選擇了更優的特徵。
如圖2所示,本發明的另一目的在於提供一種基於矩陣的低秩稀疏人臉識別系統,所述低秩稀疏人臉識別系統包括:
特徵提取模塊,用於對任意人臉樣本進行特徵提取;
識別結果模塊,用於針對特徵提取後數據進行判別分類並給出人臉識別結果。
所述特徵提取模塊中包括:
初始化單元,用於初始化迭代步驟t=1,初始化u(0)為隨機列正交矩陣,p(0)為隨機矩陣,g(0)為單位矩陣;
求投影空間單元,用於通過迭代操作,求出稀疏投影子空間p;
歸一化單元,用於將計算得到的進行歸一化處理,其公式為:
計算人臉特徵矩陣單元,用於計算映射後的人臉特徵矩陣,其公式為:
yi=ptxip(i=1,...,n)。
所述求投影空間單元中包括:
判斷模塊,用於判斷迭代過程中t的大小是否大於tmax;如小於等於tmax,則執行計算模塊,如大於tmax,則執行歸一化單元;
計算模塊,用於利用矩陣x,u(t-1),p(t-1)和函數式計算得出其函數式為:
更新模塊,用於利用等式關係將矩陣p(t)進行更新,其中等式:
分解模塊,對做svd分解得到
矩陣更新模塊,用於通過函數式對矩陣進行更新並且使得t=t+1,其中函數式:
所述識別結果模塊中還包括:
分類單元,用於對提取後的訓練集和測試集的數據使用最近鄰分類器進行判別分類。
在人臉識別中求得稀疏、有鑑別力的投影矩陣用於把圖像映射到代維空間。
基於矩陣表示的低秩稀疏人臉識別方法,屬於模式識別技術領域。該方法的核心思想是用線性稀疏的投影矩陣從高維度的圖像中提取出有鑑別力的特徵,從而提高人臉識別的效率。相較於傳統的基於向量表示的人臉識別方法,本發明直接對圖像矩陣進行特徵提取,大大加快了算法的計算速度。同時為了增強算法的魯棒性,我們採用最近較為流行的l*範數替代傳統的子空間學習方法中的l1範數或l2範數作為矩陣距離度量,使用該範數的方法又稱低秩學習方法。還有,通過加入l2,1範數正則項,算法能對迭代求解過程中有鑑別力的投影進行選擇,從而達到聯合稀疏的效果,這不僅使得投影結果具有更高的可解釋性,還可以進一步提升算法的魯棒性。實驗結果表明,通過使用l*範數和加入聯合稀疏性,該方法提高了人臉識別的性能以及穩定性。
以上所述僅為本發明的較佳實施例而已,並不用以限制本發明,凡在本發明的精神和原則之內所作的任何修改、等同替換和改進等,均應包含在本發明的保護範圍之內。
