基於先驗DEM數據的星載SAR圖像幾何精校正方法與流程

2023-06-05 07:04:46 1

本發明屬於信號處理技術領域，特別涉及一種基於先驗dem數據的星載sar圖像幾何精校正方法，適用於減小星載sar因為系統誤差造成的sar圖像場景中的像素點成像位置偏離真實位置點的問題，從而改善星載sar的成像質量，有助於用戶對sar圖像的判讀和解譯。

背景技術：

星載sar是從空間對地觀測的一種有效手段，具有全天時、全天候、多波段及高解析度的優點，能夠詳細、準確地測繪地形、地貌，獲取地球表面的信息，最終生成目標場景的高分辨地圖。

但是星載sar在從雷達脈衝的發射一直到最後通過成像算法生成星載sar圖像的過程中，會有很多非理想因素誤差引入其中，這樣會使得實際得到的星載sar圖像中每個像素點對應的場景中位置和實際場景中的位置都會有一定的偏移，使得實際得到的星載sar圖像與真實場景並不完全對應，進而無法詳細、準確地測繪地形、地貌，獲取地球表面的信息。

技術實現要素：

針對上述現有技術存在的不足，本發明的目的在於提出一種基於先驗dem數據的星載sar圖像幾何精校正方法，該種基於先驗dem數據的星載sar圖像幾何精校正方法使用星載sar回波數據進行成像處理，得到實際星載sar圖像，然後由星載sar的pos數據結合rd模型定位星載sar所在場景中每個像素點的坐標，利用ulaby模型產生後向散射係數矩陣，反演出理想的星載sar圖像，理想的星載sar圖像和實際sar圖像進行比對，求出兩者之間的偏移量，從而修正實際sar圖像因全鏈路非理想因素而引起的系統誤差，最終完成星載sar圖像的幾何精校正。

為達到上述技術目的，本發明採用如下技術方案予以實現。

一種基於先驗dem數據的星載sar圖像幾何精校正方法，包括以下步驟：

步驟1，獲取待校正的實際星載sar圖像，所述待校正的實際星載sar圖像為p×n維矩陣，p表示待校正的實際星載sar圖像的方位向包含的像素點個數，n表示待校正的實際星載sar圖像的距離向包含的像素點個數，p、n分別為大於0的正整數；

步驟2，建立待校正的實際星載sar圖像的距離都卜勒模型，記為成像模型，然後利用所述成像模型對待校正的實際星載sar圖像中的p×n個像素點分別進行定位，分別得到待校正的實際星載sar圖像中p×n個像素點各自的定位坐標；

步驟3，根據待校正的實際星載sar圖像中p×n個像素點各自的定位坐標，計算得到待校正的實際星載sar圖像中p×n個像素點各自的電磁波入射角；

步驟4，根據待校正的實際星載sar圖像中p×n個像素點各自的電磁波入射角對待校正的實際星載sar圖像進行反演，得到最終反演的理想星載sar圖像；

步驟5，分別計算待校正的實際星載sar圖像相對於最終反演的理想星載sar圖像在方位向的像素偏差量na，以及待校正的實際星載sar圖像相對於最終反演的理想星載sar圖像在距離向的像素偏差量nr；

步驟6，根據待校正的實際星載sar圖像相對於最終反演的理想星載sar圖像在方位向的像素偏差量na，以及待校正的實際星載sar圖像相對於最終反演的理想星載sar圖像在距離向的像素偏差量nr，對待校正的實際星載sar圖像進行幾何精校正，得到幾何精校正後的實際星載sar圖像。

本發明與現有的技術相比具有以下優點：

第一，本發明利用先驗dem信息，可以實現無控制點的圖像幾何精校正，不需要在在場景中布置角反射器，減少了工作量，提高了效率。

第二，本發明中利用了srtm庫中的dem來提高定位精度，從而使星載sar圖像的反演更加準確，提高了幾何精校正的準確性。

附圖說明

下面結合附圖和具體實施方式對本發明作進一步詳細說明。

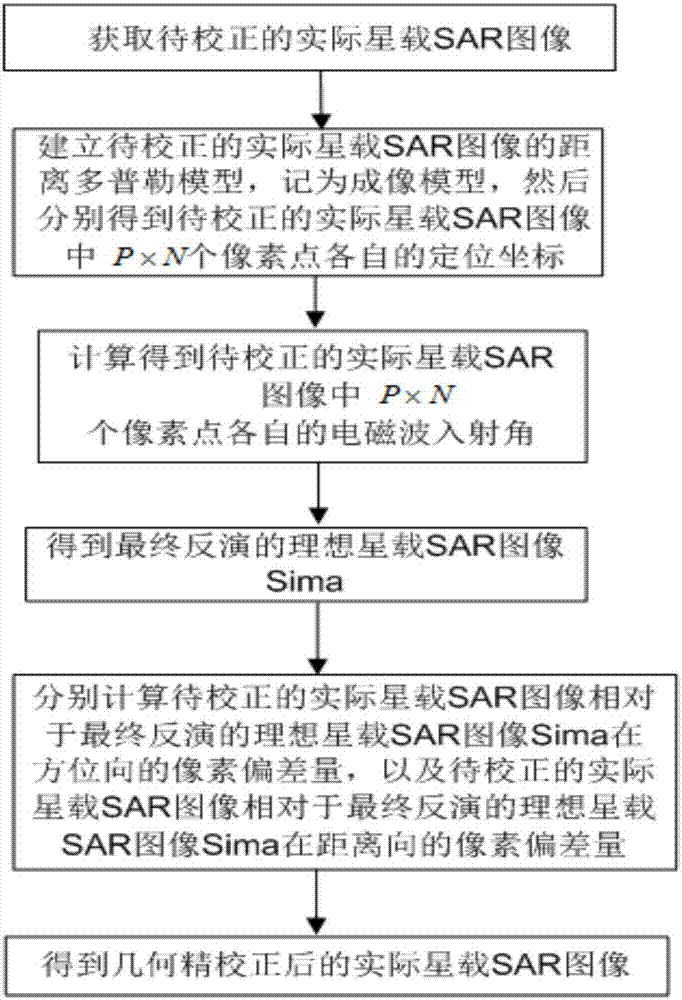
圖1為本發明的一種基於先驗dem數據的星載sar圖像幾何精校正方法流程圖；

圖2為待校正的實際星載sar圖像的距離都卜勒模型示意圖；

圖3為求解待校正的實際星載sar圖像中j個像素點各自的定位坐標的流程圖；

圖4為計算待校正的實際星載sar圖像中的像素點電磁波入射角過程示意圖；

圖5為將幾何精校正後的實際星載sar圖像中p×n個像素點分別轉換到經緯度坐標系中的過程示意圖；

圖6為高分三號星載sar圖像示意圖；

圖7a為圖6中地形起伏較大的山地部分示意圖；

圖7b為根據本發明方法對幾何精校正後的圖7a中每一個像素點分別進行反演後得到的理想星載sar圖像示意圖；

圖8為對圖6進行幾何精校正後得到的星載sar圖像示意圖；

圖9為圖8經過地理編碼後得到的結果示意圖；

圖10為對圖9中的每一個像素點進行評估後的結果示意圖。

具體實施方式

參照圖1，為本發明的一種基於先驗dem數據的星載sar圖像幾何精校正方法流程圖；其中所述基於先驗dem數據的星載sar圖像幾何精校正方法，包括以下步驟：

步驟1，獲取待校正的實際星載sar圖像，所述待校正的實際星載sar圖像為p×n維矩陣，p表示待校正的實際星載sar圖像的方位向包含的像素點個數，n表示待校正的實際星載sar圖像的距離向包含的像素點個數，p、n分別為大於0的正整數。

具體地，確定星載sar，並獲取星載sar回波數據，然後通過sar成像算法對獲取的星載sar回波數據進行成像處理，得到待校正的實際星載sar圖像；也可以直接下載網上提供的僅僅進行了成像處理的初級sar圖像。

步驟2，建立待校正的實際星載sar圖像的距離都卜勒模型，記為成像模型，然後利用所述成像模型對待校正的實際星載sar圖像中的p×n個像素點分別進行定位，分別得到待校正的實際星載sar圖像中p×n個像素點各自的定位坐標。

2.1建立待校正的實際星載sar圖像的距離都卜勒模型，如圖2所示，在所述距離都卜勒模型中，衛星沿著自身軌道飛行，且衛星自帶的gps會對星載雷達的空間位置坐標進行記錄，星載雷達位於衛星上，星載雷達的空間位置包括m個點，m個點各自的坐標都是wgs84坐標系中的坐標，wgs84坐標系的原點是地球的中心；赤道和0度經線的交點，與地球中心的連線構成wgs84坐標系的x軸；北極點和地球的中心連線構成wgs84坐標系的z軸，再由右手坐標系原則確定出wgs84坐標系的y軸；將星載雷達的空間位置包括的m個點中第i個點記為si，i＝1,2,3,...,m，第i個點的坐標為(xi,yi,zi)，xi表示第i個點si在wgs84坐標系的x軸坐標值，yi表示第i個點si在wgs84坐標系的y軸坐標值，zi表示第i個點si在wgs84坐標系的z軸坐標值；將m個點各自的坐標記為星載雷達pos數據，星載雷達pos數據對應包括m個pos數據；將m個點各自的坐標進行逐點連接後形成星載雷達航跡。

根據星載雷達pos數據，並由速度和位移關係，計算得到星載雷達的空間位置中第l個點處的瞬時速度prf表示為脈衝重複頻率,sl+1表示第l+1個點,sl表示第l個點,m表示星載雷達的空間位置包含的點個數,與pos數據個數取值相等。

星載雷達在衛星軌道上飛行的過程中，會向地面發射電磁波，就像黑夜裡牆頭上的手電筒傾斜的照射到地面上，在地面上形成一個橢圓形的光照區域一樣，星載雷達發射的電磁波照射到地面上時也會形成一個橢圓的照射區域，隨著星載雷達從第1個pos數據到第m個pos數據運動，該橢圓的照射區域會慢慢在地面上移動，直到星載雷達運動到第m個pos數據的位置,對應橢圓的照射區域形成一個長方形條帶，將所述長方形條帶記為合成孔徑雷達(sar)圖像成像區域,sar圖像成像區域對應一個長方形條帶。

將與星載雷達航跡平行的sar圖像成像區域的對應方向,記作sar圖像成像區域的方位向；將與星載雷達航跡垂直的sar圖像成像區域的對應方向,記作sar圖像成像區域的距離向，且sar圖像成像區域對應待校正的實際星載sar圖像，待校正的實際星載sar圖像的方位向包含p個像素點，待校正的實際星載sar圖像的距離向包含n個像素點，因此待校正的實際星載sar圖像為p×n維矩陣。

2.2rd模型即距離都卜勒模型，距離都卜勒模型的提出是為了對待校正的實際星載sar圖像中的p×n個像素點分別進行定位，即利用m個pos數據結合成像模型對sar圖像成像區域中的p×n個像素點分別進行定位。

將待校正的實際星載sar圖像中第m行、第n列處的像素點記作tmn，tmn的坐標記作(xmn,ymn,zmn),xmn表示待校正的實際星載sar圖像中第m行、第n列處的像素點在wgs84坐標系的x軸坐標值，ymn表示待校正的實際星載sar圖像中第m行、第n列處的像素點在wgs84坐標系的y軸坐標值，zmn表示待校正的實際星載sar圖像中第m行、第n列處的像素點在wgs84坐標系的z軸坐標值。

星載雷達空間位置包含的點個數與待校正的實際星載sar圖像的方位向包含的像素數個數取值相同，且一一對應；將第i個點si和待校正的實際星載sar圖像中第m行、第n列處的像素點tmn之間的斜距記為n＝1,2,3,…,n，m＝1,2,3,…,p，i和m取值相同，且通過星載雷達開始接收回波的時間和星載雷達接收的回波在距離向的採樣率求出,且tstarti表示星載雷達的空間位置中第i個點si開始接收回波的時間,fs表示星載雷達的距離向採樣率,c為光速；由此可以看出,第i個點si和待處理的實際星載sar圖像中第m行、第n列處的像素點tmn之間的斜距與m無關。

對於待校正的實際星載sar圖像中p×n個像素點各自的坐標，通過對應得到p×n個斜距均求解出來。

2.3以下通過三個非線性方程組去求解待校正的實際星載sar圖像中第m行、第n列處的像素點tmn的坐標。

方程一：距離方程

星載雷達開始接收回波時間和星載雷達接收的回波距離向採樣率都是已知的，對於待校正的實際星載sar圖像中的每個像素點，通過星載雷達開始接收回波的時間和星載雷達接收的回波距離向採樣率準確確定每個像素點反射回波到星載雷達的時間，因而可以知道星載雷達與該像素點的距離，如圖1中所示；也就是說，通過距離方程得到第i個點si和待校正的實際星載sar圖像中第m行、第n列處的像素點tmn之間的斜距記為其滿足方程如下：

顯然只用方程(1)無法求出待校正的實際星載sar圖像中第m行、第n列處的像素點tmn，要解出tmn的坐標(xmn,ymn,zmn),必須尋找其他方程。

方程二：都卜勒方程：

計算得到星載雷達的都卜勒頻率fd求解方法如下：

其中表示星載雷達的徑向速度，→表示矢量，λ表示為星載雷達載頻對應的波長；對於本發明要研究的問題，計算得到第i個點si和待校正的實際星載sar圖像中第m行、第n列處的像素點tmn之間的斜距對應的都卜勒頻率其表達式為：

其中，表示星載雷達的空間位置中第l個點處的瞬時速度矢量，通過pos數據可以求解；表示第i個點si和待校正的實際星載sar圖像中第m行、第n列處的像素點tmn之間的斜距矢量，→表示矢量，λ為星載雷達載頻對應的波長，||表示求絕對值操作。

星載雷達採取正側視觀測模式時，星載雷達的空間位置中第l個點處的瞬時速度矢量和垂直，因此第i個點si和待校正的實際星載sar圖像中第m行、第n列處的像素點tmn之間的斜距對應的都卜勒頻率取值為0，所以

方程三：待校正的實際星載sar圖像中第m行、第n列處的像素點tmn滿足的地球橢球方程為：

其中，re為地球的赤道半徑，rp為地球的極地半徑，re和rp都是已知量；h表示待校正的實際星載sar圖像中第m行、第n列處的像素點tmn的海拔高度，且h是未知量；xmn表示待校正的實際星載sar圖像中第m行、第n列處的像素點在wgs84坐標系的x軸坐標值，ymn表示待校正的實際星載sar圖像中第m行、第n列處的像素點在wgs84坐標系的y軸坐標值，zmn表示待校正的實際星載sar圖像中第m行、第n列處的像素點在wgs84坐標系的z軸坐標值；n＝1,2,3,…,n，m＝1,2,3,…,p，p表示待校正的實際星載sar圖像的方位向包含的像素點個數，n表示待校正的實際星載sar圖像的距離向包含的像素點個數。

因為待校正的實際星載sar圖像所在場景是地球上的某一區域，所以將該區域內像素點的坐標分別代入地球橢球方程中，在h已知的情況下，將滿足等式(4)。

聯立方程(1)、(3)、(4)三個方程，三個未知數(假設h已知)，分別計算得到待校正的星載實際sar圖像中第m行、第n列處的像素點tmn的坐標(xmn,ymn,zmn)，求解完成也就意味著完成待校正的實際星載sar圖像中第m行、第n列處的像素點tmn的定位。

2.4使用迭代法求解一組方程，來對待校正的實際星載sar圖像中第m行、第n列處的像素點tmn進行定位，tmn的坐標為(xmn,ymn,zmn)，xmn表示待校正的實際星載sar圖像中第m行、第n列處的像素點在wgs84坐標系的x軸坐標值，ymn表示待校正的實際星載sar圖像中第m行、第n列處的像素點在wgs84坐標系的y軸坐標值，zmn表示待校正的實際星載sar圖像中第m行、第n列處的像素點在wgs84坐標系的z軸坐標值；n＝1,2,3,…,n，m＝1,2,3,…,p，p表示待校正的實際星載sar圖像的方位向包含的像素點個數，n表示待校正的實際星載sar圖像的距離向包含的像素點個數，m和n的初始值分別為1。

假設h已知，並聯立式(1)、式(3)和式(4)三個方程，三個未知數，通過求解方程組得出待校正的實際星載sar圖像中第m行、第n列處的像素點坐標；而實際情況中，一般是不知道sar圖像場景中每一個像素點的海拔高度的，也就是說式(1)、式(3)和式(4)三個方程中包含四個未知數，三個方程，顯然是無法求解的；這種情況下，本發明解決策略是先假設待校正的實際星載sar圖像中第m行、第n列處的像素點海拔高度為0。

參照圖3，為求解待校正的實際星載sar圖像中j個像素點各自的定位坐標的流程圖；初始化：令f表示第f次迭代，f的初始值為1，令h0表示待校正的實際星載sar圖像中每個像素點的海拔高度預設值，其中每個像素點分別為sar圖像場景中每個像素點；設定待校正的實際星載sar圖像中包含j個像素點，令j表示第j個像素點，j∈{1,2,…,j}，j的初始值為1，j＝p×n。

2.5將第f-1次迭代後第j個像素點的海拔高度預設值hf-1帶入方程(4)，並根據式(1)和式(3)，得到如下方程組：

其中，xi表示第i個點si在wgs84坐標系的x軸坐標值，xjf表示第f次迭代後第i個點si在wgs84坐標系的x軸坐標值，yi表示第i個點si在wgs84坐標系的y軸坐標值，yjf表示第f次迭代後第i個點si在wgs84坐標系的y軸坐標值，zi表示第i個點si在wgs84坐標系的z軸坐標值，zjf表示第f次迭代後第i個點si在wgs84坐標系的z軸坐標值，表示第f次迭代後第i個點si和待校正的實際星載sar圖像中第j個像素點之間的斜距，fdjf表示第f次迭代後第i個點si和待校正的實際星載sar圖像中第j個像素點之間的斜距對應的都卜勒頻率，表示星載雷達的空間位置中第i個點處的瞬時速度矢量，表示第f次迭代後第i個點si和待校正的實際星載sar圖像中第j個像素點之間的斜距矢量，→表示矢量，λ表示星載雷達載頻對應的波長，||表示求絕對值操作，re表示地球的赤道半徑，hj(f-1)表示第f-1次迭代後第j個像素點的海拔高度預設值，rp表示地球的極地半徑。

求解以上方程組，三個方程，三個未知數，計算得到第f次迭代後第j個像素點的坐標(xjf,yjf,zjf)，所述第f次迭代後第j個像素點的坐標(xjf,yjf,zjf)是在wgs84坐標系中的，將(xjf,yjf,zjf)轉換到經緯度坐標系中，其轉換過程直接調用matlab中的坐標轉換函數ecef2lla，即將第f次迭代後第j個像素點的坐標(xjf,yjf,zjf)轉換到了經緯度坐標系中，得到第f次迭代後第j個像素點的經緯度坐標(ljf,bjf,hjf)，其中ljf為第f次迭代後第j個像素點的經度，bjf為第f次迭代後第j個像素點的緯度，hjf為第f次迭代後第j個像素點的海拔高度。

然後利用太空梭雷達地形測繪使命(srtm)資料庫中的數字高程模型(dem)數據去找出地球上經緯度(ljf,bjf)對應的海拔高度hjf'，hjf'為經緯度(ljf,bjf)對應的標準海拔高度,且此時的第f-1次迭代後第j個像素點的海拔高度預設值hf-1和hjf'不相等；其中，所述srtm資料庫中的dem數據為先驗dem數據。

2.6如果|hf-1-hjf'|≥ε0,ε0表示設定的門限閾值，本實施例中ε0＝10-2，則令f加1，將經緯度(ljf,bjf)對應的海拔高度hjf'作為第f-1次迭代後第j個像素點的海拔高度預設值hf-1，返回2.5。

如果|hf-1-hjf'|<ε0，則迭代停止，並將迭代停止時得到的第f次迭代後第j個像素點的坐標(xjf,yjf,zjf)，作為待校正的實際星載sar圖像中第j個像素點的定位坐標。

2.7令j加1，返回2.5，直到得到待校正的實際星載sar圖像中第1個像素點的定位坐標至待校正的實際星載sar圖像中第j個像素點的定位坐標，此時求得了待校正的實際星載sar圖像中j個像素點各自的定位坐標，完成了待校正的實際星載sar圖像中j個像素點各自的準確定位，j＝p×n。

步驟3，根據待校正的實際星載sar圖像中p×n個像素點各自的定位坐標，計算得到待校正的實際星載sar圖像中p×n個像素點各自的電磁波入射角。

具體地，步驟2結束後可得到待校正的實際星載sar圖像中p×n個像素點各自的準確定位，在星載雷達的pos數據已知的情況下，根據空間幾何關係得到每個像素點處電磁波的局部入射角，為下一步的反演星載sar圖像作準備。

參照圖4，為計算待校正的實際星載sar圖像中的像素點電磁波入射角過程示意圖；步驟3的子步驟為：

3.1根據向量夾角計算公式，計算得到待校正的實際星載sar圖像中第m行、第n列處像素點的電磁波入射角θmn：

其中，tmn表示待校正的實際星載sar圖像中第m行、第n列處的像素點，tm(n+2)表示待校正的實際星載sar圖像中第m行、第n+2列處的像素點，當n＝n-1時，待校正的實際星載sar圖像中第m行、第n+1列處的像素點tm(n+1)不存在，直接捨去，即記為0；當n＝n時，待校正的實際星載sar圖像中第m行、第n+2列處的像素點tm(n+2)不存在，直接捨去，即記為0；si表示第i個點，n＝1,2,3,…,n，n+2＝1,2,3,…,n，m＝1,2,3,…,p，i＝1,2,3,…,m，p表示待處理的實際星載sar圖像的方位向包含的像素數個數，m表示星載雷達的空間位置包含的點個數，i和m取值相等且一一對應；·表示點乘,*表示乘法，n表示待校正的實際星載sar圖像的距離向包含的像素點個數，→表示矢量。

3.2令m不變，且n分別取1至n，重複執行3.1，進而分別得到待校正的實際星載sar圖像中第m行、第1列處像素點的電磁波入射角θm1至待校正的實際星載sar圖像中第m行、第n列處像素點的電磁波入射角θmn，記為待校正的實際星載sar圖像中第m行n個像素點的電磁波入射角θm。

3.3令m分別取1至p，重複執行3.2，進而分別得到待校正的實際星載sar圖像中第1行n個像素點的電磁波入射角θ1至待校正的實際星載sar圖像中第p行n個像素點的電磁波入射角θp，記為待校正的實際星載sar圖像中p×n個像素點各自的電磁波入射角。

步驟4，根據待校正的實際星載sar圖像中p×n個像素點各自的電磁波入射角，以及ulaby地物散射係數經驗模型，對待校正的實際星載sar圖像進行反演，得到最終反演的理想星載sar圖像sima。

步驟4的子步驟為：

4.1根據大量的實驗和研究，待校正的實際星載sar圖像的幅度與其電磁波入射角存在近似關係；即根據待校正的實際星載sar圖像中第m行、第n列處像素點的電磁波入射角θmn，計算得到理想星載sar圖像中第m行、第n列處像素點的幅度amn：

amn＝1-sin(θmn)(7)

其中，sin表示求正弦操作。

4.2令m不變，且n分別取1至n，重複執行4.1，進而分別得到理想星載sar圖像中第m行、第1列處像素點的幅度am1至理想星載sar圖像中第m行、第n列處像素點的幅度amn，記為理想星載星載sar圖像中第m行n個像素點的幅度am。

4.3令m分別取1至p，重複執行4.2，進而分別得到理想sar圖像中第1行n個像素點的幅度a1至理想星載sar圖像中第p行n個像素點的幅度ap，記為理想星載sar圖像中p×n個像素點各自的幅度。

上述的公式(7)是表示的一個近似關係，而且並沒有考慮到雷達的工作頻率、極化方式、地物類型等因素對後向散射係數的影響；要想得出更為準確的反演sar圖像，需要用到ulaby地物散射係數經驗模型。

4.4ulaby地物散射係數經驗模型是美國密西根大學f.t.ulaby和m.c.dobson提出的一個簡單靈活的模型，他們二人綜合了20實際60年代至80年代公開發表的大量地面後向散射係數測量數據，提出了ulaby模型經驗公式，來更加準確的由電磁波入射角計算場景的後向散射係數，進而計算得到基於ulaby地物散射係數經驗模型的理想星載sar圖像中第m行、第n列處像素點的幅度σmn：

σmn(db)＝p1+p2exp(-p3θmn)+p4cos(p5θmn+p6)(8)

其中，db是分貝的單位，cos表示求餘弦操作，exp表示指數函數，p1表示ulaby地物散射係數經驗模型的常數項，p2表示ulaby地物散射係數經驗模型的指數係數項，p3表示ulaby地物散射係數經驗模型的指數相位項，p4表示ulaby地物散射係數經驗模型的三角係數項，p5表示ulaby地物散射係數經驗模型的三角相位係數項，p6表示ulaby地物散射係數經驗模型的三角相位常數項；p1、p2、p3、p4、p5和p6都是考慮星載雷達工作波段、星載雷達發射信號的極化方式、觀測星載雷達所在場景的地物類型等因素，並經過大量實驗而得出的經驗值，詳細數值可以參見雷達手冊。

4.5令m不變，且n分別取1至n，重複執行4.4，進而分別得到基於ulaby地物散射係數經驗模型的理想星載sar圖像中第m行、第1列處像素點的幅度σm1至基於ulaby地物散射係數經驗模型的理想星載sar圖像中第m行、第n列處像素點的幅度σmn，記為基於ulaby地物散射係數經驗模型的理想星載sar圖像中第m行n個像素點的幅度σm。

4.6令m分別取1至p，重複執行4.5，進而分別得到基於ulaby地物散射係數經驗模型的理想星載sar圖像中第1行n個像素點的幅度σ1至基於ulaby地物散射係數經驗模型的理想星載sar圖像中第p行n個像素點的幅度σp，記為基於ulaby地物散射係數經驗模型的理想星載sar圖像中p×n個像素點各自的幅度，並將所述基於ulaby地物散射係數經驗模型的理想星載sar圖像中p×n個像素點各自的幅度作為經過反演得到的理想星載sar圖像，簡記為最終反演的理想星載sar圖像sima。

步驟5，分別計算待校正的實際星載sar圖像相對於最終反演的理想星載sar圖像sima在方位向的像素偏差量na，以及待校正的實際星載sar圖像相對於最終反演的理想星載sar圖像sima在距離向的像素偏差量nr。

步驟5的子步驟為：

5.1對待校正的實際星載sar圖像和最終反演的理想星載sar圖像sima進行配準可以使用很多方法，本發明採用相關函數法在頻域實現，將待校正的實際星載sar圖像和最終反演的理想星載sar圖像sima分別變換到二維頻域，分別得到待校正的實際星載sar圖像的二維頻譜s2f，以及最終反演的理想星載sar圖像的二維頻譜σ2f，其表達式分別為：

s2f＝fft(fft(sreal))(9)

σ2f＝fft(fft(σmn))(10)

其中，fft表示做快速傅立葉變換操作，sreal表示待校正的實際星載sar圖像，σmn表示最終反演的理想星載sar圖像sima，下標2f表示二維頻域。

使用max函數分別確定待校正的實際星載sar圖像的二維頻譜s2f的峰值位置和最終反演的理想星載sar圖像的二維頻譜σ2f的峰值位置，然後比較s2f的峰值位置和σ2f的峰值位置的偏差，分別將s2f的峰值位置記作(samax，srmax)，將σ2f的峰值位置記作(σamax，σrmax)，samax表示待校正的實際星載sar圖像的二維頻譜最大值所在位置在方位向的坐標值，srmax表示待校正的實際星載sar圖像的二維頻譜最大值所在位置在距離向的坐標值，σamax表示最終反演的理想星載sar圖像的二維頻譜最大值所在位置在方位向的坐標值，σrmax表示最終反演的理想星載sar圖像的二維頻譜最大值所在位置在距離向的坐標值。

5.2進而分別計算得到待校正的實際星載sar圖像相對於最終反演的理想星載sar圖像sima在方位向的像素偏差量na，以及待校正的實際星載sar圖像相對於最終反演的理想星載sar圖像sima在距離向的像素偏差量nr，其表達式分別為：

na＝samax-σamax(11)

nr＝srmax-σrmax(12)。

步驟6，根據待校正的實際星載sar圖像相對於最終反演的理想星載sar圖像sima在方位向的像素偏差量na，以及待校正的實際星載sar圖像相對於最終反演的理想星載sar圖像sima在距離向的像素偏差量nr，使用matlab中二維插值函數interp2對待校正的實際星載sar圖像進行幾何精校正，得到幾何精校正後的實際星載sar圖像。

具體地，根據待校正的實際星載sar圖像相對於最終反演的理想星載sar圖像在方位向的像素偏差量na，以及待校正的實際星載sar圖像相對於最終反演的理想星載sar圖像距離向的像素偏差量nr，使用matlab中二維插值函數interp2對幾何精校正後的實際星載sar圖像進行幾何精校正，得到幾何精校正後的實際星載sar圖像，即分別令x為幾何精校正後的實際星載sar圖像中第x行,x＝1,2,3,…,p；y為幾何精校正後的實際星載sar圖像中第y列,y＝1,2,3,…,n，p表示待處理的實際星載sar圖像的方位向包含的像素數個數，與幾何精校正後的實際星載sar圖像的列數取值相等；n表示待校正的實際星載sar圖像的距離向包含的像素點個數，與幾何精校正後的實際星載sar圖像的行數取值相等。

將幾何精校正後的實際星載sar圖像中第x行、第y列處的像素點記為重採樣後的實際星載sar圖像srxy，srxy＝interp2(x，y，sreal，x+nr，y+na)，sreal表示待校正的實際星載sar圖像，interp2表示matlab中二維插值函數。

x＝1,2,3,…,p，y＝1,2,3,…,n，遍歷待校正的實際星載sar圖像中p×n個像素點，進而得到幾何精校正後的實際星載sar圖像。

步驟7，對幾何精校正後的實際星載sar圖像進行地理編碼，得到地理編碼後的幾何精校正星載sar圖像。

具體地，幾何精校正後的實際星載sar圖像中p×n個像素點的坐標都是wgs84坐標系中的，現在將幾何精校正後的實際星載sar圖像中p×n個像素點分別轉換到經緯度坐標系中；使用matlab中自帶的一個函數ecef2lla將幾何精校正後的實際星載sar圖像中p×n個像素點分別轉換到經緯度坐標系中，其轉換過程如圖5所示。

圖5中的左圖是幾何精校正後的實際星載sar圖像，圖4中的右圖是由經度軸和緯度軸組成的經緯度坐標系；當知道幾何精校正後的實際星載sar圖像中每一個像素點的wgs84坐標後，通過ecef2lla函數將幾何精校正後的實際星載sar圖像中每一個像素點的wgs84坐標分別轉換到經緯度坐標系中，具體為：

7.1令幾何精校正後的實際星載sar圖像中第m行、第n列處的像素點為t'mn，t'mn的wgs84坐標為(x'mn,y'mn,z'mn)，x'mn表示幾何精校正後的實際星載sar圖像中第m行、第n列處的像素點t'mn在wgs84坐標系中x軸的坐標值，y'mn表示幾何精校正後的實際星載sar圖像中第m行、第n列處的像素點t'mn在wgs84坐標系中y軸的坐標值，z'mn表示幾何精校正後的實際星載sar圖像中第m行、第n列處的像素點t'mn在wgs84坐標系中z軸的坐標值。

將幾何精校正後的實際星載sar圖像中第m行、第n列處的像素點t'mn的wgs84坐標對應轉換到經緯度坐標系中，得到幾何精校正後的實際星載sar圖像中第m行、第n列處的像素點經緯度坐標(lmn,bmn,hmn)，lmn表示幾何精校正後的實際星載sar圖像中第m行、第n列處像素點的經度值，bmn表示幾何精校正後的實際星載sar圖像中第m行、第n列處像素點的緯度值，hmn表示幾何精校正後的實際星載sar圖像中第m行、第n列處像素點的高度值。

7.2令m不變，且n分別取1至n，重複執行7.1，進而分別得到幾何精校正後的實際星載sar圖像中第m行、第1列處的像素點經緯度坐標(lm1,bm1,hm1)至幾何精校正後的實際星載sar圖像中第m行、第n列處的像素點經緯度坐標(lmn,bmn,hmn)，記為幾何精校正後的實際星載sar圖像中第m行n個像素點的經緯度坐標。

7.3令m分別取1至p，重複執行7.2，進而分別得到幾何精校正後的實際星載sar圖像中第1行n個像素點的經緯度坐標至幾何精校正後的實際星載sar圖像中第p行n個像素點的經緯度坐標，記為幾何精校正後的實際星載sar圖像中p×n個像素點各自的經緯度坐標，並將所述幾何精校正後的實際星載sar圖像中p×n個像素點各自的經緯度坐標作為地理編碼後的幾何精校正星載sar圖像。

結合實測數據對本發明效果作進一步驗證說明。

參照圖6，為高分三號星載sar圖像示意圖，圖6中每個像素點的經緯度和實際經緯度都是存在偏差的，這些偏差是由於星載雷達的系統誤差造成的。

圖7a為圖6中地形起伏較大的山地部分示意圖；用所述地形起伏較大的山地部分確定星載sar圖像的系統誤差，從而完成幾何精校正。

圖7b為根據本發明方法對幾何精校正後的圖7a中每一個像素點分別進行反演後得到的理想星載sar圖像示意圖；

圖8為對圖6進行幾何精校正後得到的星載sar圖像示意圖；

選取圖8所在場景中的一個像素點來驗證幾何精校正的效果，圖8上半部分是城區，在密集的城區中有一塊矩形的建築區，如圖8中的十字線處，選取圖8矩形建築區的右下角這個像素點進行驗證。

用googleearth準確找出這個像素點的經緯度高程坐標為：(34.896336，112.816433，113)，第一個參數是緯度，第二個參數是經度，第三個參數是高程，該經緯度高程坐標是該像素點的實際坐標。

在未進行幾何精校正之前，經過定位這個點的經緯度高程為：(34.897016，112.817699，113)，這個坐標和實際坐標的距離誤差為138.1368m。

進行幾何精校正之後，這個點的經緯度高程為：(34.896536，112.816483，113)，這個坐標和實際坐標的距離誤差為22.6720m。

可以看出，經過本專利的幾何精校正技術，sar圖像中像素點的位置更加準確，sar圖像的利用價值更高；圖6和圖8整體看上去差距不大，但是選擇其中的一個點去進行評估，就會發現經過幾何精校正後的圖像比校正之前，每個像素點的位置有了更為精確的改善；圖9為圖8經過地理編碼後得到的結果示意圖；圖10為對圖9中的每一個像素點進行評估後的結果示意圖。

綜上所述，仿真實驗驗證了本發明的正確性，有效性和可靠性。

顯然，本領域的技術人員可以對本發明進行各種改動和變型而不脫離本發明的精神和範圍；這樣，倘若本發明的這些修改和變型屬於本發明權利要求及其等同技術的範圍之內，則本發明也意圖包含這些改動和變型在內。