一種鐵路網結構可靠度的度量方法與流程
2023-10-20 04:20:52 2
本發明涉及一種度量方法,準確地說是一種鐵路網結構可靠度的度量方法,用於鐵路網可靠度的計算。
背景技術:
近年來,交通運輸網絡可靠性成為交通運輸領域的熱點研究問題。影響交通運輸網絡可靠性的因素既有外部的,如自然災害和恐怖襲擊等,又有內部的,如運輸需求、路網結構等。很多文獻從不同角度考察交通運輸網絡可靠性,提出了各種交通運輸網絡可靠性的定義。根據現有文獻,交通運輸網絡可靠性是一個大的概念,它包含多個互不相同,但互相聯繫的可靠性,如基礎設施的可靠性、連通可靠性、通行時間可靠性、運輸能力可靠性、抗毀可靠性等,路網結構在交通運輸網絡可靠性的研究中沒有引起關注。很顯然,不同的路網結構導致不同的路網運行狀態,包括不同的交通運輸網絡可靠性。因此,路網結構可靠性與其它可靠性應具有同等的重要性。交通運輸網絡可靠性包含很多要素,其中最重要的應該是路網結構可靠性,在路網結構可靠的前提下,路網的性能才會可靠。
此外,作為交通運輸網絡的一種,鐵路網規劃設計時,常需要對兩個或多個路網結構進行比較,從中挑選較優方案。從可靠性角度講,實際上是對兩個或多個規模相同、投資相同、運輸組織方式相同,但結構不同的鐵路網,在承載相同運輸需求下,對路網結構進行可靠度比較。
但現在缺少操作性較好的結構可靠度測度方法,特別是在規定時間及規定條件下,鐵路網承受一定載荷而不癱瘓的能力。
技術實現要素:
本發明要解決的技術問題是,本方法可以測試在規定時間及規定條件下,鐵路網承受一定載荷而不癱瘓的能力,為路網結構進行可靠度比較提供一種可行的方法。
為解決上述技術問題,本發明採用如下技術手段:
一種鐵路網結構可靠度的度量方法,包括以下步驟:
1)根據鐵路網各區段飽和度來計算路網飽和度:
1.1)計算區段能力利用率,它是區段車流量與通過能力的比值;區段ej的能力利用率為:
式中,vj為區段j車流量,而cj為區段ej通過能力;
1.2)計算鐵路網飽和率為:
式中,m表示鐵路網飽和區段數,區段飽和的概念是區段的能力利用率達到擁擠程度,根據國際慣例,雙線區段0.8,單線區段是0.75,具體到我國的情況,可為0.9;m為鐵路網總區段數;
2)計算運輸需求未滿足率
其中fk為第k個od對的實際實現的流量,為所有od對實際實現流量的總和,也是路網運輸能力,是所有od對的運輸需求總量,即總運輸需求量;
3)定義鐵路網癱瘓的概率:p=θ(1+λ),0≤p≤1;(4)4)鐵路網結構承載度r1為:r1=1-p=1-θ(1+λ)
5)計算鐵路網區段和節點的抗毀度為:
式中,h為有效路徑區段關聯矩陣,h的橫坐標值表示區段編號,縱坐標值表示有效路徑編號,h由元素0和1組成,hij=0表示i區段不在有效路徑j上,hij=0表示i區段在有效路徑j上;hx為矩陣h的第x個列向量;ωl表示區段或節點被破壞後,受其影響路網中不能正常運行的區段集;為區段或節點受到破壞後所影響的交通量;為鐵路網中的總交通量;∑or為邏輯或運算;有效路徑區段關聯矩陣h由元素0和1組成,引入邏輯或運算,用or表示;
邏輯或運算的運算規則:or(0,0)=0;or(0,1)=or(1,0)=1;or(1,1)=1;在此基礎上,定義矩陣邏輯或運算:設有m×n維矩陣s,t,則[or(sm×n,tm×n)]ij=or(sij,tij);把基於矩陣邏輯或運算的連續運算符號記為∑or;
取承載度與抗毀度複合計算結構可靠度,既能測試鐵路網在正常運營條件下的可靠度,又能測試鐵路網在自然災害或人為破壞情況下的可靠度;
6)取區段和節點抗毀度的方差的函數作為鐵路網抗毀度r2,即
式中,e為區段集,區段是兩個相鄰節點之間的連線,/e/=m;j為節點集,/j/=n;τl為子系統l抗毀度;τavg為所有子系統(區段及節點)的平均抗毀度;
區段和節點抗毀度的均方差作為鐵路網的抗毀度,可有效反映鐵路網在意外情況下保持完整運營的能力;
7)計算鐵路網結構可靠度:r=(r1+r2)/2。
採用上述技術方案的本發明,與現有技術相比,其突出的特點是:本方法可以測試在規定時間及規定條件下,鐵路網承受一定載荷而不癱瘓的能力,為路網結構進行可靠度比較提供一種可行的方法。且本技術方案取承載度與抗毀度複合計算結構可靠度,既能測試鐵路網在正常運營條件下的可靠度,又能測試鐵路網在自然災害或人為破壞情況下的可靠度;另外,本技術方案將區段和節點抗毀度的均方差作為鐵路網的抗毀度,可有效反映鐵路網在意外情況下保持完整運營的能力。
進一步的優選技術方案如下:
採用蒙特卡羅摸擬法模擬運輸需求及運輸能力隨機變化情況下結構可靠度的特性,並將結構可靠度的抽樣均值做為結構可靠度的期望值。
一般情況下,鐵路網的各條區段通過能力服從[θc,c](式中,c是區段的設計通過能力,0<θ<1)的均勻分布,而各節點對之間的運輸需求服從正態分布。於是,結構可靠度是隨機變量,可用圖2算法模擬運輸需求及運輸能力隨機變化情況下結構可靠度的特性,並將結構可靠度的抽樣均值做為結構可靠度的期望值,計算鐵路網在車流波動情況下的結構可靠度。
本發明的優點與積極作用在於:
1、計算複雜度很低,可操作性好;2、既能測試鐵路網在正常運營條件下的可靠度,又能測試鐵路網在自然災害或人為破壞情況下的可靠度;3、方法有效度高:路網結構的微小不同,會引起路網運行狀態明顯差別;這種結構可靠度可有效反映路網結構不同所導致的運行狀態差別。
附圖說明
圖1是本發明的流程圖。
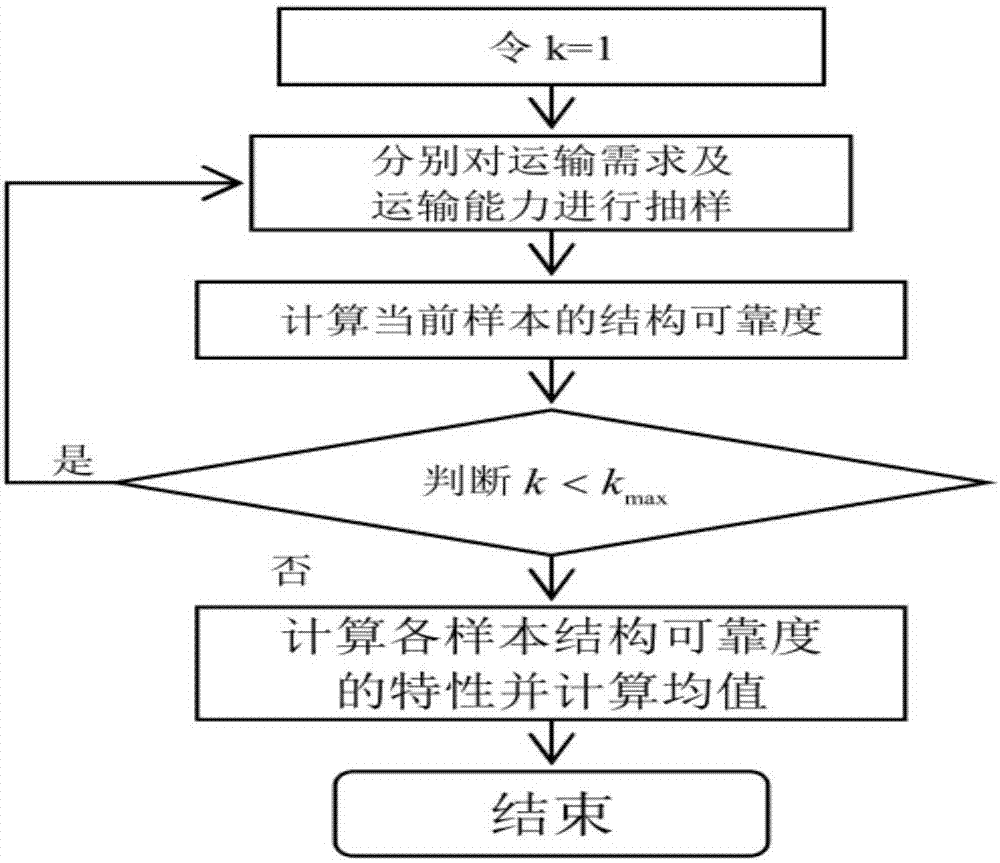
圖2是本發明結構可靠度的蒙特卡羅模擬算法流程圖。
具體實施方式
下面結合實施例,進一步說明本發明。
參見圖1可知,本發明的一種鐵路網結構可靠度的度量方法,包括以下步驟:
1)計算區段能力利用率,它是區段車流量與通過能力的比值。區段j的能力利用率為:j=1,2,...,m,式中,vj為區段j車流量,而cj為區段ej通過能力。
2)計算鐵路網飽和率為:0≤θ≤1,式中,m表示鐵路網飽和的區段數,區段飽和的概念是區段的能力利用率達到擁擠程度,根據國際慣例,雙線區段是0.8,單線區段是0.75,具體到我國的情況,可為0.9;m為鐵路網總區段數。
3)計算運輸需求未滿足率
其中fk---第k個od對的實際實現的流量,k∈k
---所有od對實際實現流量的總和,也可以說是路網運輸能力。
是所有od對的總運輸需求量。
4)定義鐵路網癱瘓的概率:p=θ(1+λ),0≤p≤1
四種極端組合分析:
當θ=0,λ=0,可得p=0,即鐵路網飽和率為零,所有區段都不飽和,所有運輸需求都能滿足,因此鐵路網癱瘓概率為零;
當θ=0,λ=1,也就是鐵路網飽和率為零,所有區段都不飽和,所有運輸需求都不滿足,這種情況實際上不會發生。
當θ=1,λ=0,可得p=1,即鐵路網飽和率為1,所有區段都飽和,所有運輸需求都滿足,則鐵路網癱瘓概率為1;
當θ=1,λ=1,即鐵路網飽和率為1,所有區段都飽和,所有運輸需求都不滿足,即沒有開始運輸,所有區段都已經飽和。這種情況不會發生,也不可能出現p=θ(1+λ)=1(1+1)=2的情況。
公式p=θ(1+λ)有可能出現p≥1的情況。如果p≥1,定義p=1。以保證下面公式正常,即r1≤1。
5)計算鐵路網結構承載度r1為:r1=1-p=1-θ(1+λ)。
6)計算鐵路網區段和節點的抗毀度;
式中,h為有效路徑區段關聯矩陣,h的橫坐標值表示區段編號,縱坐標值表示有效路徑編號。h由元素0和1組成,hij=0表示i區段不在有效路徑j上,hij=1表示i區段在有效路徑j上。
hx為矩陣h的第x個列向量。
ωl表示區段或節點l被破壞後,受其影響路網中不能正常運行的區段集。
為區段或節點l受到破壞後所影響的交通量。
為交通運輸網絡中的總交通量。
在本步驟中,定義了一種新的運算:∑or為邏輯或運算。有效路徑區段關聯矩陣h由元素0和1組成,引入邏輯或運算,用or表示。邏輯或運算的運算規則是這樣的:or(0,0)=0;or(0,1)=or(1,0)=1;or(1,1)=1。在此基礎上,定義矩陣邏輯或運算:設有m×n維矩陣s,t,則
[or(sm×n,tm×n)]ij=or(sij,tij)。
把基於矩陣邏輯或運算的連續運算符號記為∑or,例如:
6)取區段和節點抗毀度的方差的函數作為鐵路網抗毀度r2,即
式中,e為區段集,區段是兩個相鄰節點之間的連線,|e|=m;j為節點集,|j|=n;τl為子系統l抗毀度;τavg為所有子系統(區段及節點)的平均抗毀度。
7)計算鐵路網結構可靠度:r=(r1+r2)/2。
8)用蒙特卡羅摸擬法來計算車流波動下的結構可靠度。
結合圖2可知,結構可靠度的蒙特卡羅模擬算法包括以下步驟:
步驟1:令計算資料k=1;
步驟2:對各區段的通過能力進行抽樣(從[θc,c]中抽樣);
步驟3:對各od點對之間的運輸需求進行抽樣,運輸需求服從以通常情況下的運輸需求為期望的正態分布;
步驟4:利用前所說的步驟1)-7)計算當前樣本的結構可靠度;
步驟5:判斷是否達到了最大樣本量k<kmax,如果是,進入步驟6,否則,令k=k+1,返回步驟2;
步驟6:計算各樣本結構可靠度的特性和均值。
承載性與抗毀性共同決定了鐵路網結構可靠度。鐵路網的承載性主要與能力利用率有關。抗毀性多與鐵路結構有關,同時也受能力利用率影響。能力利用率受車流波動影響,尖峰時段能力利用率較高,而非尖峰時段能力利用率較低。因此,計算結構可靠度應考慮車流波動。一般情況下,可假定各條區段通過能力服從[θc,c](式中,c是區段的設計通過能力,0<θ<1)的均勻分布,而各節點對之間的運輸需求服從正態分布。於是,結構可靠度是隨機變量。附圖1所示的算法模擬運輸需求及運輸能力隨機變化情況下結構可靠度的特性,並將結構可靠度的抽樣均值做為結構可靠度期望值。
以上所述僅為本發明的具體實施方式,但本發明的保護不限於此,任何本技術領域的技術人員所能想到本技術方案技術特徵的等同的變化或替代,都涵蓋在本發明的保護範圍之內。
