一種多元時序數據的模式預測方法與流程
2023-12-07 02:34:59 3
本發明屬於計算機領域,特別涉及計算機中的數據挖掘領域,具體涉及一種多元時序數據的模式預測方法。
背景技術:
時序預測在天氣預報,股票等領域是一個非常重要的研究方向。在時序預測中一個最重要的方法就是能夠根據一些變量的趨勢去預測其他變量的行為,這就叫做多元時序預測。例如,如果我們認為兩個變量相關,那我們可能想知道例如在天氣預報中溫度增加了10%是否影響了溼度的趨勢。
在多元預測中,我們可以將主要的一些方法分成數學和人工的方法。數學方法中如arima(autoregressiveintegratedmovingaveragemodel,將非平穩時間序列轉化為平穩時間序列,然後將因變量僅對它的滯後值以及隨機誤差項的現值和滯後值進行回歸所建立的模型)或者指數平滑算法在處理真實世界中的非線性無規律數據時均不可靠。人工神經網絡、支持向量機和k近鄰都是一些應用於時間序列預測的機器學習方法。然而由於很多的時間變量會隨著時間平移和伸縮,這些傳統的方法就會失效。為了解決這個問題,一個解決方案就是考慮一個序列的行為而不是考慮一個變量值。例如一些方法在時間序列分析中進行模式預測。這些方法都假定一種對數據表示然後盡力去尋找最頻繁的模式。然而,這些解決方案存在的主要問題是:這些方法中數據表示並沒有降低數據維數尤其是高維數據,而且他們還必須去用例如聚類的方法處理數據導致時間複雜度提高;另外一個問題是他們的研究沒有能力解釋輸出規則和關係,因此時間複雜度的減小和解釋輸出規則和關係需要得要有效的解決。
技術實現要素:
針對現有技術的缺陷和不足,本發明的目的是提供一種多元時序數據的模式預測方法,解決現有的數據處理方法時間複雜度高的問題。
為了實現上述目的,本發明採用如下技術方案予以實現:
一種多元時序數據的模式預測方法,包括以下步驟:
階段一:對每一個條件變量及決策變量所形成的時間序列尋找候選興趣模式集,分別對每個候選興趣模式集進行聚類;
步驟1:尋找候選興趣模式集;
步驟1.1:尋找可用初始子序列
對於時間序列s={s1,…,sl},從s1開始依次尋找斜率m1≠0的兩個相鄰時間序列值,將首次尋找到的兩個相鄰時間序列值作為初始子序列si={si,si+1},其中,i=1,2,…,l-1,l為時間序列的長度,斜率m1的計算公式為:
步驟1.2:計算相鄰時間序列值的斜率
給可用初始子序列增加下一個si+2,計算si+2和si+1的斜率m2;
步驟1.3:獲取興趣模式
如果m2不等於m1,得到興趣模式pα={si,si+1,si+2};
如果m2等於m1,繼續步驟1.2,直到mk不等於m1為止,得到興趣模式pα={si,si+1,…,si+k},其中,mk為si+k和si+k-1的斜率,k=1,2,…,l-2;
步驟1.4獲取候選興趣模式集
對於時間序列s={s1,…,sl},從興趣模式pα的最後一個時間序列值開始,重複步驟1.1至步驟1.3,直到找到整個時間序列s={s1,…,sl}中所有的興趣模式,形成候選興趣模式集pc={p1,p2,…,pα,…,pβ,…,pn};
步驟2:候選興趣模式集聚類;
步驟2.1:利用以下剪枝規則①和剪枝規則②給滿足規則條件的模式距離值賦為無窮大;
剪枝規則①:如果候選興趣模式集pc中的任意兩個興趣模式pα,pβ沒有同時出現在區域寬度為ws的同一區域中,將距離矩陣d中的dαβ賦為無窮大;其中,ws是用戶指定的參數,d為興趣模式的距離矩陣,
dαβ=dαβ(pα,pβ),dαβ為pα和pβ的歐幾裡德距離;
剪枝規則②:如果興趣模式pα的斜率為負,且興趣模式pβ的斜率為正,將距離矩陣d中的dαβ賦為無窮大;
步驟2.2:計算距離矩陣中dαβ為非無窮大的元素的距離,並賦值到距離矩陣中相應的位置;
步驟2.3:比較dαβ(pα,pβ)和用戶指定的dmin之間的大小,若dαβ≤dmin,從pc中刪除pα和pβ兩個興趣模式中時間序列值的個數較小的興趣模式,最終得到新的興趣模式集p;
其中,dmin取相鄰兩個時間序列值之間的歐幾裡德距離最小值和最大值之間的某個值,具體由用戶指定;
階段二:產生預測規則
步驟3:用apriori算法計算關聯規則
合併每個時間變量的興趣模式集p得到pall,利用apriori算法對pall中的興趣模式進行關聯規則挖掘,獲取不同時間變量間的多個關聯規則;
步驟4:生成預測規則
①把m(pvm)=m(p′)=1的多個關聯規則合併形成如下的預測規則:
a1≤v(pv1)≤b1,且a2≤v(pv2)≤b2,…,且aj≤v(pv)j≤bj,…,且aλ≤v(pvλ)≤b,則c1≤v(p′)≤c2,並且延遲δt1個單位時間;
其中,pvj是條件變量形成的興趣模式,j=1,2,…,λ,λ≥1,λ為條件變量的個數,p′是決策變量形成的興趣模式;
m(pvm)是sl和s1之間的斜率,m(pvm)=sgn(sl-s1),pvm是條件變量中對決策變量影響最大的興趣模式,sl是pvm中最後一個時間序列值,s1是pvm中第一個時間序列值;m(p′)是s′l和s1′之間的斜率,s′l代表p′中最後一個時間序列值,s1′代表p′中第一個時間序列值;
aj和bj分別是m(pvm)=m(p′)=1的興趣模式關聯規則中v(pvj)的最小值和最大值,c1和c2分別是m(pvm)=m(p′)=1的興趣模式關聯規則中v(p′)的最小值和最大值,aj、bj、c1和c2均是正數;
v(pvj)是條件變量中興趣模式pvj的變化量,v(p′)是決策變量中興趣模式p′的變化量,
v(pvj)=(max(pvj)-min(pvj))×m(pvj)
v(p′)=(max(p′)-min(p′))×m(p′)
max(pvj)和min(pvj)分別表示興趣模式pvj的最大時間序列值和最小時間序列值;
時延δt1=max(δ(rg)),δ(rg)=ipvm-ip′,ipvm是pvm的起始時間值,ip′是p′的起始時間值;
②把m(pvm)=m(p′)=-1的多個關聯規則合併形成如下的預測規則:
e1≤v(pv1)≤f1,且e2≤v(pv2)≤f2,…,且ej≤v(pv)j≤f,j…,且eη≤v(pvη)≤fη,則g1≤v(p′)≤g2,並且延遲δt2個單位時間;
其中,ej和fj分別是m(pvm)=m(p′)=-1的興趣模式關聯規則中v(pj)的最小值和最大值,g1和g2分別是m(pvm)=m(p′)=-1的興趣模式關聯規則中v(p′)的最小值和最大值,j=1,2,…,η,η≥1,η為條件變量的個數;ej、fj、g1和g2均是負數,j為自然數;δt2=max(δ(rg));
階段三:將待測數據的條件變量執行階段一獲得的興趣模式去匹配階段二的預測規則,若滿足預測規則的前件,則輸出決策變量的預測結果。
進一步的,所述的步驟2中候選興趣模式集聚類方法可以用如下方法替換:
步驟2.1:利用r-tree構建候選模式集中的每個模式的mbr,形成模式的數據結構,得到模式的索引;
步驟2.2:對r-tree數據結構中的每個孩子節點i和j,利用以下剪枝規則1和規則2給滿足規則條件的模式距離值賦為無窮大。
剪枝規則①:如果兩個興趣模式pα,pβ沒有同時出現在區域寬度為ws的同一區域中,將距離矩陣中的dαβ賦為無窮大;其中,ws是用戶指定的參數,d為興趣模式的距離矩陣,
dαβ=dαβ(pα,pβ),dαβ為pα和pβ的歐幾裡德距離;
剪枝規則②:如果興趣模式pα的斜率為負,且興趣模式pβ的斜率為正,將距離矩陣d中的dαβ賦為無窮大;
步驟2.3:距離矩陣d中dαβ為非無窮大的元素按照歐幾裡德距離進行計算,並賦值到距離矩陣中相應的位置;
步驟2.4:比較dαβ(pα,pβ)和用戶指定的dmin之間的大小,若dαβ≤dmin,從pc中刪除pα和pβ兩個興趣模式中時間序列的個數較小的興趣模式,最終得到新的興趣模式集p;其中,dmin取相鄰兩個時間序列之間的歐幾裡德距離最小值和最大值之間的某個值,具體由用戶指定。
與現有技術相比,本發明的有益效果是:本發明的多元時序數據的模式預測方法計算量小,有效的減小模式預測中的時間複雜度,解決了傳統方法中時間複雜度過高的問題。
附圖說明
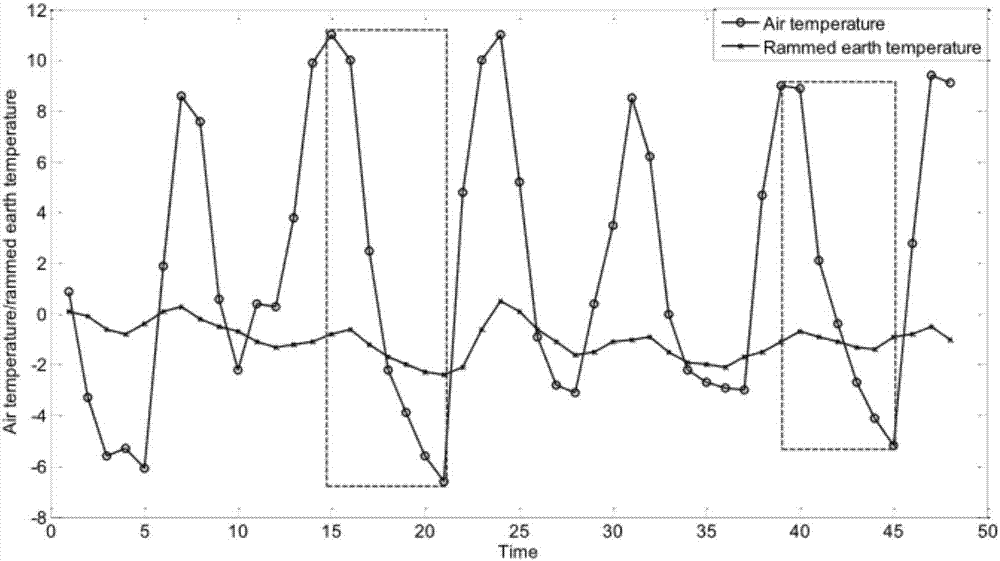
圖1是空氣溫度和夯土溫度的時序圖。
圖2是空氣溫度和夯土溫度的變量關係圖。
圖3是模式間的mbr。
圖4是本發明所提出的用於檢索候選模式的基於r-tree的數據結構圖。
圖5是歐幾裡得距離測量的使用剪枝與未使用剪枝策略進行距離矩陣計算的性能與序列號圖。
圖6是使用剪枝規則的歐氏距離計算所用的時間和使用剪枝和r-tree進行距離矩陣計算的時間性能比較圖。
圖7是實施例中生成的六個規則的性能評價。
以下結合實施例對本發明的具體內容作進一步詳細解釋說明。
具體實施方式
本發明中的條件變量是能夠用來預測其他變量的變量,決策變量就是可以被其他變量預測的變量。
本發明的方法過程分為三個階段:
階段一:對每一個條件變量及決策變量所形成的時間序列尋找候選興趣模式集,分別對每個候選興趣模式集進行聚類;階段二:產生預測規則;階段三:根據階段二生成的預測規則對待測數據進行預測。
其中階段一和階段二是訓練階段,將已有的數據執行階段一和階段二後得到預測規則,階段三是針對待測量的數據,將待測量數據經歷階段一後獲得的興趣模式去匹配階段二中的預測規則,若滿足預測規則的前件,則輸出決策變量的預測結果。
在階段一中:尋找興趣模式,並總結數據的行為,對於數據的變化,尋找斜率為正和斜率為負的模式。由於序列數據可能包含重複的模式,該算法對這些模式進行聚類和分組,具體為:
步驟1:尋找候選興趣模式集
步驟1.1:尋找可用初始子序列
對於時間序列s={s1,…,sl},從s1開始依次尋找斜率m1不為0的兩個相鄰時間序列值,將首次尋找到的兩個相鄰時間序列值作為初始子序列si={si,si+1},其中,i=1,2,…,l-1,l為時間序列的長度,斜率m1的計算公式為:
步驟1.2:計算相鄰時間序列值的斜率
給可用初始子序列增加下一個si+2,計算si+2和si+1的斜率m2;
步驟1.3:獲取興趣模式
如果m2不等於m1,得到興趣模式pα={si,si+1,si+2};
如果m2等於m1,繼續步驟1.2,直到mk不等於m1為止,得到興趣模式pα={si,si+1,…,si+k},其中,mk為si+k和si+k-1的斜率,k=1,2,…,l-2;
步驟1.4獲取候選興趣模式集
對於時間序列s={s1,…,sl},從興趣模式pα的最後一個時間序列值(即si+k)開始,重複步驟1.1至步驟1.3,直到找到整個時間序列s={s1,…,sl}的n個興趣模式,形成候選興趣模式集pc={p1,p2,…,pα,…,pβ,…,pn};
步驟2:候選興趣模式集聚類;
在候選模式集中將相似模式分組,尋找相似模式的第一步是在模式之間生成一個距離矩陣。對於每一對模式,一個距離矩陣的元素顯示了兩個模式的距離。然而傳統的算法的時間消耗太大,為了解決這個問題,本發明中提出了兩種方法:一種為剪枝規則,另一種為r-tree結合剪枝規則。
對於剪枝規則,具體如下:
步驟2.1:利用以下剪枝規則①和剪枝規則②給滿足規則條件的模式距離值賦為無窮大;
剪枝規則①:如果候選興趣模式集pc中的任意兩個興趣模式pα,pβ沒有同時出現在區域寬度為ws的同一區域中,那麼這兩個模式的距離為無窮大,將距離矩陣d中的dαβ賦為無窮大;其中,ws是用戶指定的參數,d為興趣模式的距離矩陣,
dαβ=dαβ(pα,pβ),dαβ為pα和pβ的歐幾裡德距離;
剪枝規則②:使用模式的斜率來進行剪枝,如果興趣模式pα的斜率為負,且興趣模式pβ的斜率為正,則它們不能被認為是相似的,將距離矩陣d中的dαβ填充為無窮大;
步驟2.2:計算距離矩陣中dαβ為非無窮大的元素之間的歐幾裡德距離,並賦值到距離矩陣中相應的位置。
步驟2.3:比較dαβ(pα,pβ)和用戶指定的dmin之間的大小,若dαβ≤dmin,從pc中刪除pα和pβ兩個興趣模式中時間序列值的個數較小的興趣模式,最終得到新的興趣模式集p;其中,dmin取相鄰兩個時間序列值之間的歐幾裡德距離最小值和最大值之間的某個值,時間序列值具體由用戶指定。
對於r-tree結合剪枝規則,r-tree用來索引候選模式集pc,如圖4所示,p1-p9為候選模式,r樹結構中每一個樹的葉結點為一個候選模式的mbr。具體如下:
步驟2.1:利用r-tree構建候選模式集中的每個模式的mbr,形成模式的數據結構,得到模式的索引;其中每一個葉子節點是一個模式的mbr,r-tree的中間項用附近的mbr來索引模式。這個數據結構通過減少處理的模式的數量將被用來減少算法的時間複雜度。圖3說明了模式p1和模式p2間的mbr。
步驟2.2:對r-tree數據結構中的每個孩子節點i和j,利用以下剪枝規則1和規則2給滿足規則條件的模式距離值賦為無窮大。
剪枝規則①:如果候選興趣模式集pc中的任意兩個興趣模式pα,pβ沒有同時出現在區域寬度為ws的同一區域中,那麼這兩個模式的距離為無窮大,將距離矩陣d中的dαβ賦為無窮大;其中,ws是用戶指定的參數,d為興趣模式的距離矩陣,
dαβ=dαβ(pα,pβ),dαβ為pα和pβ的歐幾裡德距離;
剪枝規則②:使用模式的斜率來進行剪枝,如果興趣模式pα的斜率為負,且興趣模式pβ的斜率為正,則它們不能被認為是相似的,將距離矩陣d中的dαβ填充為無窮大;
步驟2.3:計算距離矩陣中dαβ為非無窮大的元素之間的歐幾裡德距離,並賦值到距離矩陣中相應的位置。
步驟2.4:比較dαβ(pα,pβ)和用戶指定的dmin之間的大小,若dαβ≤dmin,從pc中刪除pα和pβ兩個興趣模式中時間序列值的個數較小的興趣模式,最終得到新的興趣模式集p;其中,dmin取相鄰兩個時間序列值之間的歐幾裡德距離最小值和最大值之間的某個值,具體由用戶指定。
階段二:產生預測規則
步驟3:用apriori算法計算關聯規則
合併每個時間變量的興趣模式集p成pall,利用apriori算法對pall中的興趣模式進行關聯規則挖掘,獲取不同時間變量間興趣模式的關聯規則:
其中,g=1,2,…,r,pvj是條件變量形成的興趣模式,p′是決策變量形成的興趣模式;
按照如下的公式計算關聯規則rg的方向、時延和變化量:
關聯規則的方向計算公式:
其中,m(pvm)是sl和s1之間的斜率,m(pvm)=sgn(sl-s1),pvm是條件變量中對決策變量影響最大的興趣模式,sl代表pvm中最後一個時間序列值,s1代表pvm中第一個時間序列值;m(p′)是s′l和s′之間的斜率,s′l代表p′中最後一個時間序列值,s′代表p′中第一個時間序列值;
時延的計算公式:
δt1=max(δ(rg)),δ(rg)=ipvm-ip′(4)
其中,ipvm是pvm的起始時間值,ip′是p′的起始時間值;
規則的變化量:
v(pvj)=(max(pvj)-min(pvj))×m(pvj)
v(p′)=(max(p′)-min(p′))×m(p′)(5)
其中,v(pvj)是條件變量中興趣模式pvj的變化量,v(p′)是決策變量中興趣模式p′的變化量,max(pvj)和min(pvj)分別表示興趣模式pvj的最大時間序列值和最小時間序列值。
步驟4:生成預測規則
①把m(pvm)=m(p′)=1的多個關聯規則合併形成如下的預測規則:
a1≤v(pv1)≤b1,且a2≤v(pv2)≤b2,…,且aj≤v(pv)j≤bj,…,且aλ≤v(pvλ)≤b,則c1≤v(p′)≤c2,並且延遲δt1個單位時間;
其中,aj和bj分別是m(pvm)=m(p′)=1的興趣模式關聯規則rg中v(pvj)的最小值和最大值,c1和c2分別是m(pvm)=m(p′)=1的興趣模式關聯規則rg中v(p′)的最小值和最大值,j=1,2,…,λ,λ≥1,λ為條件變量的個數,aj、bj、c1和c2均是正數。
②把m(pvm)=m(p′)=-1的多個關聯規則合併形成如下的預測規則:
e1≤v(pv1)≤f1,且e2≤v(pv2)≤f2,…,且ej≤v(pv)j≤f,j…,且eη≤v(pvη)≤fη,則g1≤v(p′)≤g2,並且延遲δt2個單位時間;
其中,ej和fj分別是m(pvm)=m(p′)=-1的興趣模式關聯規則中v(pj)的最小值和最大值,g1和g2分別是m(pvm)=m(p′)=-1的興趣模式關聯規則中v(p′)的最小值和最大值,ej、fj、g1和g2均是負數,j=1,2,…,η,η≥1,η為條件變量的個數;δt2=max(δ(rg)),δ(rg)=ipvm-ip′,ipvm是pvm的起始時間值,ip′是p′的起始時間值;
本發明使用命中率h用於說明本發明算法的性能,h定義為:
其中,n為條件變量中準確匹配預測規則的興趣模式的數目,m為條件變量中興趣模式的總數目。
以下給出本發明的具體實施例,需要說明的是本發明並不局限於以下具體實施例,凡在本申請技術方案基礎上做的等同變換均落入本發明的保護範圍。
實施例1
本實施例給出將本發明算法用於預測明長城遺址的土體溫度,其中,圖1和圖2分別為明長城遺址空氣溫度和夯土溫度的時序圖及其變量關係圖,將該時序數據通過上述三個階段的處理,其中,本實施例在階段一中只使用了剪枝規則候選興趣模式集聚類,其結果如圖5,其中,naive曲線表示的是既不使用剪枝規則也不使用r-tree數據結構的聚類結果,pruning-based曲線表示使用剪枝規則的聚類結果,從圖中可以看出,隨著時間序列數量的增加,未使用剪枝規則的歐氏距離計算所用的時間程指數增長,而使用了剪枝規則進行距離計算的時間增長緩慢。
實施例2
本實施例與實施例1的區別點在於:本實施例在階段一中使用了r-tree的數據結構結合剪枝規則候選興趣模式集聚類,這個數據結構通過減少處理的模式的數量將被用來減少算法的時間複雜度,如圖6所示。橫軸是時間序列的數量,可以看到隨著時間序列數量的增加,使用剪枝規則結合r-tree進行距離矩陣計算的時間比僅使用剪枝規則進行距離矩陣計算的時間增長緩慢。在空氣溫度的時序圖中,p1和p2為本發明算法識別的候選模式集,可以構建兩個模式間的mbr,圖3所示為模式p1和模式p2之間的mbr。
表1為本實施例生成的六個具體的預測規則,
表1預測規則
圖7是本實施例根據上述六個預測規則的預測結果,圖中橫軸為監測區域,縱軸為命中率。圖7中展示了生成的六個預測規則在區域1,2,3,4,5中進行預測的命中率h的對比結果,其中規則3的平均命中率最高。
